Численное моделирование лучистых тепловых потоков на поверхность спускаемого аппарата, движущегося в атмосфере Венеры

Исследования новых планет представляют большой интерес для современной науки. Особенно важной задачей является исследование Венеры, так как она обладает схожими с Землёй размерами и составом, однако её температура и атмосфера радикально отличаются из-за парникового эффекта и других факторов.

Десантные модули (ДМ), предназначенные для исследования Венеры, будут вынуждены столкнуться с сильным давлением и атмосферным нагревом. Результаты, полученные в [6] и [7], демонстрируют, что радиационный теплообмен становится доминирующим фактором теплового воздействия. В таких экстремальных условиях требуется разработка многослойной теплозащитной системы, обеспечивающей эффективное распределение и отвод тепла. Это позволит аппарату выдерживать предполагаемые тепловые нагрузки и предотвратит критические перегревы элементов конструкции. Ключевым аспектом тепловых нагрузок является лучистый тепловой поток от ударного слоя на поверхность десантного модуля, количественная оценка которого представляет основную задачу данного исследования. В теоретической работе [8] был разработан метод расчета радиационного нагрева для венерианских условий, однако для новых миссий типа «Венера-Д» требуются уточненные модели, учитывающие последние данные об атмосферном составе планеты.

2.    Цель работы

Целью данной работы является разработка методики расчета лучистых тепловых потоков, воздействующих на теплозащитный экран спускаемого аппарата при входе в атмосферу Венеры со второй космической скоростью в условиях неравновесного физикохимического взаимодействия, с последующей визуализацией полученных результатов в виде полей распределения тепловых потоков по поверхности аппарата.

3.    Динамика излучающего газа

При высоких скоростях полета в космосе, в частности при спуске космического корабля на поверхность планет, температура газа может быть очень высокой, а плотность газа очень низкой. В результате тепловое излучение становится очень важным видом переноса тепла.

Явление теплового излучения рассматривается с макроскопической точки зрения [1]. Следовательно, линейные размеры в поле потока больше по сравнению с длиной волны излучения и масштаб времени больше по сравнению с периодом всех частот, содержащихся в излучении.

Тепловые лучи можно характеризовать спектральной интенсивностью излучения Д. Она представляет собой количество электромагнитной энергии, распространяющейся в рассматриваемом направлении за единицу времени, отнесенное к единице телесного угла, к единице поверхности, нормальной к этому направлению, и к единице частотного интервала.

Интегральную интенсивность излучения можно определить как

I = I Д dv.

Результирующий поток излучения на единицу площади в единицу времени в направлении L представляет собой общее количество энергии, излучаемой по всему спектру во всех направлениях, т. е.

q = У I cos в de.

Направление L однозначно определяется угловыми координатами в(0 < в < т) и азимутальным углом ?(0 < <у? < 2т). Элементарный телесный угол de, ограниченный пределами (в + de) и (9? + d^), будет равен de = sin eded?.

Тогда уравнение для результирующего потока излучения принимает вид q (0,p,r,t) =          I Iy (0,p,r,t) sin 0 cos 0d0dpdp,

0    0     0

где r — координата положения текущей точки.

В большинстве инженерных, а также астрофизических задач рассматривается перенос излучения относительно плоской поверхности. Удобно разбить результирующий поток излучения q на две части: одна часть q+ представляет составляющую в направлении нормального единичного вектора п, а другая часть q- — составляющую в противоположном направлении, т. е.

q+ (0, p,r,t) = [ ( [   I_y (0, p, r, t) sin 0 cos 0 d0 dip dp,

0    0     0

q- (0,p,r,t) = — II I  I_y (0,p,r,t) sin 0 cos 0d0dpdp.

0    0    ^/2

Тогда результирующий поток излучения будет q = q+ + q-.

Обычно принимают, что нормаль п направлена к поверхности. Следовательно, поток q⁺ связан с лучами, направленными к поверхности, в то время как поток q^- связан с лучами, направленными от поверхности. Результирующий тепловой поток — поток, направленный к поверхности.

Поскольку в данном исследовании рассматривается падающий на поверхность спускаемого аппарата лучистый тепловой поток, а вклад рассеяния в газовой среде пренебрежимо мал, величина потока не зависит от радиационных характеристик поверхности и ее температуры. Поэтому в рамках решаемой задачи справедливо утверждать, что q = q+.

Кинетическое уравнение, описывающее изменение спектральной интенсивности излучения I_y во времени и в пространстве, называется уравнением переноса излучения.

4.    Уравнение переноса излучения

Спектральная интенсивность является результатом взаимодействия между излучением и веществом, которое следовало бы изучить с микроскопической точки зрения с помощью квантовой механики. Однако для практических задач течения потока основной интерес представляет макроскопическая точка зрения. Точные результаты микроскопического анализа могут быть осреднены с помощью некоторых коэффициентов, представляющих средние значения физических свойств рассматриваемой среды. В задачах переноса излучения физические свойства среды могут быть выражены в виде спектрального коэффициента поглощения к у и спектрального коэффициента излучения j y. Коэффициент поглощения описывает, насколько эффективно материал поглощает излучение на различных длинах волн, а коэффициент излучения описывает способность тела излучать электромагнитное излучение на определенной длине волны.

Предполагается, что среда является гомогенной, так что свойства поглощения и излучения изменяются в среде непрерывно.

Уравнение переноса излучения по существу является законом сохранения энергии излучения. Оно записывается следующим образом:

= - ¹     + к у (J y — I y ) ,                              (1)

os с at где Jy — функция источника излучения, s — направление светового луча.

В газодинамике температура газа обычно не постоянна во всем поле течения, но в каждой точке этого поля можно определитв локалвнуго температуру Т, чтобы описатв свойства газа в этой точке. В результате хорошим приближением для большинства задач радиационной газодинамики является допущение, что газ находится в локальном термодинамическом равновесии, при котором спонтанное испускание излучения зависит только от локальной температуры Т и плотности газа.

Расчет лучистого потока на поверхность ДМ в неравновесном приближении требует применения гибридной схемы расчета лучистого теплопереноса. В ней используется многотемпературное локальное термодинамическое равновесие, где предполагается, что каждая точка поля описывается температурами, соответствующими разным степеням свободы: поступательной, колебательной, электронной и вращательной. В данной работе неравновес-ность физико-химических процессов в ударном слое моделируется с применением двухтемпературного приближения, которое учитывает раздельное описание поступательной и колебательной температур. Данный подход обусловлен существованием разных характерных времен релаксации различных степеней свободы молекулярных компонентов газа. Такая методика расчета включает расчет колебательной температуры с помощью решения уравнений релаксации колебательной энергии и расчет поступательной температуры из решения уравнений Навье - Стокса без учета радиационного члена. А из уравнений химической кинетики находятся массовые концентрации газовых компонент в ударном слое. Эта работа проделана в [5] с использованием решателя hy2Foam на основе платформы OpenFOAM для десантного модуля «Венера-Д». Из [5] были взяты данные по полям колебательных и поступательных температур и массовых концентраций для данной работы.

В локальном термодинамическом равновесии излучение и поглощение связаны между собой через функцию Планка излучения чёрного тела в соответствии с законом Кирхгофа. В функции Планка берётся колебательная температура, так как функция Планка выводится для излучения между колебательными уровнями энергии, заселенность которых описывается распределением Больцмана с колебательной температурой. Влиянием отличия вращательной температуры от колебательной в функции Планка пренебрегается.

Тогда, применяя двухтемпературное локальное термодинамическое равновесие (рассчитываются поступательная и колебательная температуры, электронная берется равной колебательной, вращательная — поступательной), и в условиях неравновесности физикохимических процессов, можно заменить функцию источника излучения на функцию Планка с колебательной температурой.

Поэтому уравнение переноса излучения (1) в случае локального термодинамического равновесия записывается как

1т = -1 +ку (Ву - ) ’ ( 2) ds с dt где В у — функция равновесного источника излучения. Во всех задачах радиационной газодинамики, связанных с течением потока, высокочастотные явления не рассматриваются. Следовательно, масштаб времени t значительно больше, чем l/с, где I — характерный размер поля течения. Так как расстояние s вдоль рассматриваемого луча должно быть того же порядка величины, как и l, то можно пренебречь нестационарным членом — | ^Д по сравнению с членом пространственного изменения интенсивности ^Д В результате уравнение переноса излучение (2) принимает вид

= к у (В у — Д) . ds

5.    Решение уравнения переноса излучения в приближении плоского слоя

Спускаемый аппарат «Венера-Д» имеет сегментально-коническуго форму. Его компоновка представлена на рис. 1. Ударный слой — область газа между ударной волной и поверхностью тела — имеет толщину, малую по сравнению с характерными размерами аппарата. В этом случае для расчета лучистого потока реальный объем газа можно аппроксимировать локально одномерным плоским слоем.

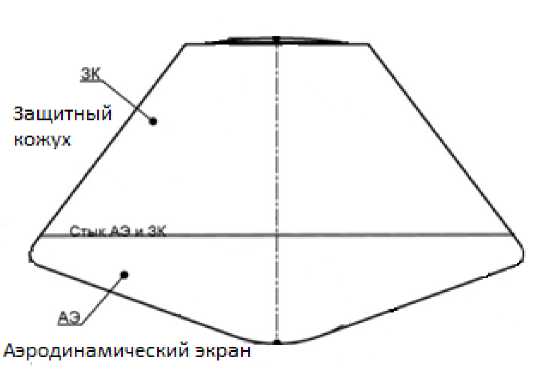
Рис. 1. Спускаемый аппарат «Вепера-Д»

Приближение локально одномерного плоского слоя играет большую роль в задачах лучистого теплообмена тел, движущихся в атмосфере с высокими скоростями.

Пусть s — расстояние, измеряемое вдоль светового луча (рис. 2). Ось Оу направлена вдоль поверхности спускаемого аппарата, а ось Ох — по нормали к его поверхности. Тогда элемент длины ds выражается как d dx cos в

.

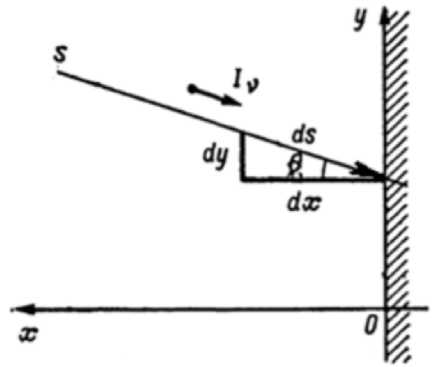
Рис. 2. Плоский слой

А уравнение переноса излучения тогда можно переписать как dlx drx (L) cos О

= k x (B x - lx] ,

где была введена оптическая толщина тд(L) = 0 ^ к д dx, L — длина нормали, dx — элемент длинв! нормали к поверхности спускаемого аппарата, 0 — угол между нормалвго и направлением светового луча. А функция равновесного источника излучения В д находится по формуле Планка:

В_Д = В (_ДТ (х)) = ^Д-( -Д- Y

А у_{е Хкт} ( ж ) - 1J

Также для удобства численных расчетов использовались определения интенсивности излучения, функции Планка, коэффициента поглощения и оптической толщины в единичном диапазоне длин волн (вместо частотного интервала).

Решение дифференциального уравнения имеет вид

В = ^с(^тд(т) cos 0

- тАП е ^cos ^ .

Чтобы найти множитель С ( T O ⁽J( ) j, входящий в решение уравнения переноса излучения, используется метод вариации постоянной:

‘ - тАЛ.   „ - TJJ 1           - тАГ)

Се cos в -Се cos в = В д - Се cos в ,

С‘ = В д е ^cosв .

Отсюда

_г У ^T Д ^(L) А  _с   р ^(L) _R д^Лд ^{( х )}

С ----л- = Со +        В д е ^cosв ----—,

\ cos 0 /           ./о                cos 0

б тДД\ cos 6

в выражение для интен-

где тд(х) = /q кд dx'. Тогда, подставив выражение для С сивности, получим т       тд(L}\ -таЛ   /     Г(('г, таЛЛтд(х)\ -таЛ

1 д = С ( ----— ) е ^{cos в} =  Со +         В д е ^{cos в} -----— е ^{cos в} .

cos 0                      о               cos 0

Чтобы найти константу Со, используется граничное условие 1 д (т д (Е) = 0) = 0, означающее отсутствие излучения при нулевой оптической толщине. Из этого условия следует, что Со = 0. Тогда решение дифференциального уравнения переноса излучения для спектральной интенсивности запишется в виде

1 д =

^ТА ^(L)

В д е

таЛ Лт д (х) cos в --------- cos 0

TJL)

- •,/•,. Л(т д (L)) - тд (х))

ВДе     cose -----------т------- cos 0

Результирующий поток излучения выражается через спектральную интенсивность как дД = 2л /   1Д cos 0 sin 0d0,                              (6)

где было уже проведено интегрирование по азимутальному углу.

После подстановки (5) в (6) выражение для потока излучения примет вид

^^/2 т^)¹            _та(ЛтаЛ    „     d(тд(L)) — тд(х))

дд = 2л              Вд(Т (х))е     cose cos 0 sin 0------------'-dd.

о ./оcos

Тогда расчетная формула для потока лучистой энергии выглядит следующим образом:

^{1 ТА}( ^ )                    та ( L ) — Ta ( ж )

дд = 2л J J      Вд (Т (х))е     cos®    d(тд(L))-тд(x))d(cos 0).(7)

Выражение (7) можно упростить, если ввести интегральную экспоненту — En(t) = ./о zn 2е t/z dz. Тогда формула для расчета лучистого потока примет вид дд = 2л I     Вд(Т(х^ЕзДдД)) - тд(х)) d(тд(L)) - тд(х)).(8)

6.    Построение нормалей для расчета лучистого потока

Для проведения расчёта лучистых потоков использовались результаты численного моделирования обтекания ДМ потоком газа в атмосфере Венеры. Была предоставлена структурированная двумерная сетка носовой части десантного модуля (рис. 3), на каждой ячейки которой нужно рассчитать тепловой поток излучения, суммированный по длинам волн, и трехмерная сетка ударного слоя (рис. 4) с полями концентраций, поступательных температур и колебательных температур компонент газа атмосферы Венеры внутри ударного слоя. Обе сетки являются осесимметричными. Данные ЗВ-геометрии и результаты расчётов обтекания были предоставлены в формате Tecplot. Из центра каждой ячейки двумерной сетки были построены нормали к поверхности, которые имеют точки пересечения с элементами трехмерной сетки ударного слоя. По этим нормалям был рассчитан лучистый поток на поверхность ДМ.

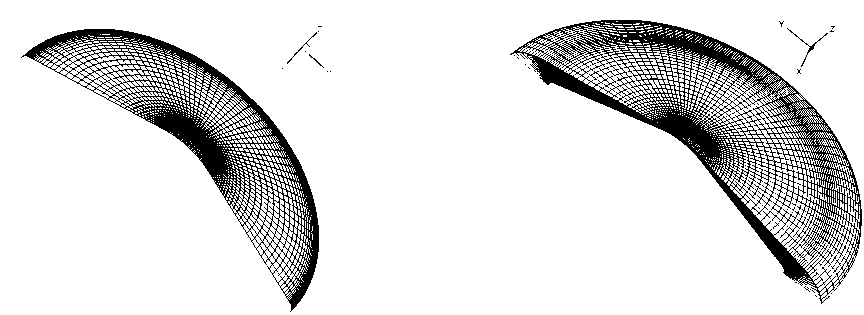
Рис. 3. Двумерная сетка поверхности десантного Рис. 4. Трехмерная сетка расчетной области модуля                                         (ударного слоя)

Нормали к поверхности спускаемого аппарата были построены с использованием методов аналитической геометрии, основанных на уравнениях поверхностей и нормалей. Для каждого элемента поверхности сначала составлялось уравнение плоскости по трем точкам:

det

^2 - ад У2 - yi ^з - а уз - У1 . X ^{- X}1 у ^- yi

Z2 - ^1

^3 - ^1 Z — Z1

= 0,

^ = (Z2 - Zi)(yi - уз ) - (yi - У2)(Z1 - Z3),

В = (X2 - Xi )(Z1 - Z3) + (Z2 - Z1 )(хз - Xi),

C = (X2 - Xi)(уз - У1 ) + (yi - У2)(xз - Xi),

D = (X2 - Xi)(zз yi - У з Zi) + (yi - y2 )(zзXi - XзZ1) + (Z2 - Zi )(уз Xi - Xзyi),

Az + Ву + Cz + D = 0.

6.1.    Уравнение нормали к плоскости из заданной точки

Нормаль будет строиться из центра элемента поверхности — точки с координатами Xo, уо, zq . Тогда параметрическое уравнение прямой, перпендикулярной элементу на плос- кости, заданной уравнением Ах + By + С z + D = 0, записывается как х = хо + ЛА,

< у = уо + ЛB,                                      (9)

z = zo + ЛС .

6.2.    Точка пересечения прямой с плоскостью

Требуется найти точки пересечения нормалей от каждой ячейки поверхности с гранями каждой трехмерной ячейки из сетки ударного слоя.

Пуств плоскость, которой принадлежит грань, задается уравнением Мх + Ny + Qz + Р = 0. Тогда, чтобы найти точку пресечения нормали, заданной параметрическим уравнением (9), с гранью, нужно подставить x,y,z из параметрического уравнения нормали в уравнение плоскости, которой принадлежит грань, и найти Л:

_ - (^Мхо + ^Nyo + ^Qzo + ^р ) = МА + NB + QC .

Затем нужно подставить параметр Л обратно в уравнение нормали. Тогда можно найти точку пересечения плоскости, на которой лежит грань трехмерной ячейки, с нормалью из двумерной ячейки поверхности.

6.3.    Проверка, принадлежит ли точка пересечения плоскости с нормалью рассматриваемой грани, которая лежит в этой плоскости

Поскольку каждая грань представляет собой четырехугольник, обозначим его вершины как ABCD. Пусть Р — точка пересечения. Если точка Р принадлежит четырехугольнику ABCD, то площадь четырехугольника выражается как S abcd = ^S apb + S b pc + S cpd + ^S apd-

Так как известны трехмерные координаты каждой вершины, то можно найти векторы AB,BC,CD,AD,AP,BP,CP,DP. Плошали треугольников S a_PB ,S _bPc ,S c_PD ,S a_PD вычисляются через векторные произведения:

Sabc = 2 |AB х AC|, а площадь четырехугольника Sabcd находится как сумма площадей треугольников Sabc + Sadc-

Данный метод корректен только при условии, что точка Р лежит в той же плоскости, что и четырехугольник ABCD. Это условие выполняется, поскольку ранее была найдена точка пересечения нормали с плоскостью, построенной по точкам этого четырехугольника.

7.    Расчет коэффициентов поглощения для атмосферы Венеры

Атмосфера Венеры состоит из молекул СО2 и N2. При высоких температурах, образующихся в ударном слое перед поверхностью ДМ, эти молекулы практически сразу же диссоциируют, образуя атомы С, О, N и молекулу СО.

Выражения для коэффициента поглощения для атомов и молекул немного отличаются. Сначала представим его вывод для молекул. Полную энергию молекулы можно представить в виде суммы электронной энергии Е_е, колебательной энергии Еу и вращательной энергии Ej:

Е = Е е + Е у + E j .

Энергия электронного движения Ее определяется кинетической энергией электронов и энергией потенциального взаимодействия электронов с ядрами и с другими электронами. В данной работе значения Ее приведены в качестве исходник данных для всех электронных уровней молекул СО и N2. Молекула СО2 не учитывается в расчетах, так как ее концентрация в ударном слое пренебрежимо мала и её вклад в излучение незначителен.

Важным элементом расчетных методик является задание потенциалов межъядерного взаимодействия двухатомных молекул [4]. В практике приближенных расчетов используются аналитические зависимости для потенциальных кривых: потенциалы Морзе, гармонический, Леннард-Джонса и другие. Для выражения колебательной энергии Е у обычно используется потенциал Морзе. Он имеет достаточно простую математическую форму, которая хорошо описывает поведение молекул, учитывая как притяжение, так и отталкивание между атомами, что делает его более реалистичным по сравнению с простыми гармоническими моделями.

Потенциал Морзе имеет следующий вид:

U (г) = De (1 — exp(-a(r — ге)))2, где De и a - постоянные, характеризующие данную молекулу (De — энергия диссоциации, отсчитываемая от минимума потенциальной энергии), ге — межъядерное расстояние.

Положение колебательных уровней энергии в случае потенциала Морзе описывается формулой

Е у = k

Ш е ^Г + 2 ^ — Ш е Х е ^Г +

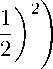
где v - колебательное квантовое число, ш_е — классическая частота собственных колебаний осциллятора, ш_ех_е — постоянная ангармоничности.

Энергия вращательного движения в приближении квантового ротатора записывается как

Ej = kBv J (J + 1), где J — вращательное квантовое число полного момента, Bv — вращательная постоянная, k — постоянная Больцмана. Каждый вращательный уровень имеет вырождение по вращательному квантовому числу, равное (2J + 1).

В пределах колебательной полосы вращательные линии образуют структуру, называемую ветвями колебательных полос, число которых бывает разным. Выделяют три основных типа ветвей: Q-ветвь образуется при вращательных переходах с AJ = 0, R-ветвь образуется при AJ = +1. В-вствь образуется при AJ = —1.

Каждая молекула, находящаяся на верхнем возбужденном уровне, может испустить фотон с энергией К ш с вероятностью А_ш (коэффициент Эйнштейна для спонтанного излучения). Полное число таких молекул составляет n2V, где П2 — плотность населенности верхнего возбужденного вращательного уровня. Соедовательно, полная мощность излучения, генерируемого молекулами с плотностью П2 в объёме V в интервале частот Аш, выражается как

/у Аш = n2V Аш Кш, где Аш — заданный спектральный интервал (шаг частотной сетки).

Энергия излучаемого фотона определяется разностью полных энергий верхнего и нижнего квантовых состояний молекулы, включающих электронную, колебательную и вращательную составляющие:

Кш = Ее2 + ЕУ2 + EJ2 — Ее1 — ЕУ1 — EJ1, где индексы «2» и «1» соответствуют верхнему и нижнему энергетическим уровням соответственно.

Согласно распределению Больцмана, плотность населённости верхнего энергетического уровня выражается как

1                              Ее.,

^Е У 2    ^E J 2

- kT y   kT j

П2 = ng2(2J2 + 1) exp — — Z                \ kTe где п — общая населенность всех уровней молекулы, д2 — статвес верхнего электронного уровня, J2 — вращательное число верхнего уровня, z — статсумма для молекулы; Te, Ту, Tj — электронная, колебательная и вращательная температуры. Согласно правилам отбора для вращательных переходов, допустимы изменения квантового числа: J2 — Ji = —1, 0,1.

Полная статсумма z представляется в виде произведения электронной (z_e), колебательной (zy) и вращательной (zj) составляющих:

^z = Z^v = £ . exp (-g) £ exp , y ) £Щ + 1) (-g ) .

По закону Кирхгофа объемное излучение связано с коэффициентом поглощения как q^ Аш = 4rV кш В ш Аш, где Вш = 4^332 enu/kT i ^ функция равновесного излучения Планка в частотном представлении.

Приравнивая выражение для полного объемного излучения к мощности спонтанного излучения, получаем выражение для коэффициента поглощения:

^к ш

= П2А_Ш Нш

4г В_ш Аш

(Ю)

Для молекул необходимо учитывать полную энергетическую структуру, включающую электронные, колебательные и вращательные степени свободы. Обычно у молекул учитывается десяток электронных уровней, несколько десятков колебательных уровней и несколько сотен вращательных уровней. В результате такого многоуровневого строения спектр молекулы содержит порядка ~ 105 спектральных линий. Коэффициент Эйнштейна можно записать с индексами переходов как

Аш = Ae2y2J2^eiyiJi, где ei — нижний электронный уровень молекулы, VyJi — колебательное и вращательное квантовые числа, характеризующие состояние молекулы на нижнем уровне; e2, V2 J2 ~ аналогичные параметры для верхнего возбуждённого уровня.

Коэффициент Эйнштейна для молекулярных переходов может быть факторизован с учетом фактора Хёнля - Лондона, который определяет относительную интенсивность вращательных линий:

Ae2y2J2 ^eiyiJi = Ae2y2^e1y1Hj2^j1, где Hj2^j1 — фактор Хёнля - Лондона, определяющий вероятность вращательного перехода J2 ^ J1, Ae2y, ,eiy1 — усреднённые по вращательной структуре коэффициенты Эйнштейна. Факторы Хёнля - Лондона удовлетворяют условию нормировки:

£ H.h -J = ¹

Для атомов применяется аналогичный молекулярному подход расчета коэффициентов поглощения, однако благодаря отсутствию колебательной и вращательной структур (имеется только электронная структура уровней), вычисления существенно упрощаются. В качестве статсуммы берется только электронная статсумма. А формула для плотности населенности верхнего возбужденного уровня выражается как

П2 =

- пд2 exp z

(—к1)’

где п — общая населенность всех уровней атомов.

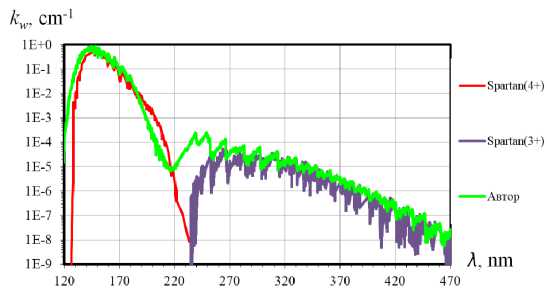
Рис. 5. Сравнение коэффициентов поглощения для СО

Коэффициент Эйнштейна А_ш для атомов дан только для электронных переходов, то есть А_ш = А_е 2 ^_е1. Выражение для коэффициента поглощения для атомов будет таким же, как и полученный в (10) для молекул, но с учетом прописанных выше изменений.

В данной работе при моделировании атомарного излучения учитывается высокая интенсивность спектральных линий, что в общем случае требует использования профиля Фойгта для корректного описания их формы. В [2, 3] представлена детальная теория профиля Фойгта. Этот профиль комплексно учитывает доплеровское, естественное и штарковское уширения. Однако в рамках настоящего исследования применено упрощённое описание, основанное на усреднении атомарных линий по спектральным интервалам.

На рис. 5 представлено сравнение спектральных зависимостей коэффициента поглощения для двух электронных переходов молекулы СО, полученных различными методами. Зелёная кривая соответствует расчёту по разработанному в данной работе алгоритму, в то время как красная и фиолетовая кривые отражают результаты моделирования двух характерных электронных переходов 3+ и 4+ в программном комплексе SPARTAN для моделирования излучения плазмы в неравновесной термодинамике.

8.    Результаты расчета излучения на поверхность спускаемого аппарата

Параметры набегающего потока брались по VIRA-30 (Venus International Reference Atmosphere) и представлены в табл 1.

Таблица!

Параметры набегающего потока (траектория ДМ)

t, с	Н, км	Ию, м/с	Мю	Re ю	РюУЮ, а™	Но, кДж/кг	Рю, Па	Тю, к
25	95.64	10382	49.73	2.84е+5	0.271	54006	8.269	168.8
30	90	9105	43.56	1.31е+6	1.00	41565	39.94	169.4
33	87.19	7550	35.36	2.03е+6	1.30	28655	76.6	175.5

Расчеты лучистых потоков на поверхность десантного модуля проводились для трех траекторных точек: 87 км, 90 км, 95 км. Были взяты именно эти траекторные точки, так как они являются самыми теплонапряженными. Траекторное движение десантного модуля осуществлялось под нулевым углом атаки.

Для расчёта распределения лучистого потока по поверхности десантного модуля «Венера-Д» использовались следующие исходные данные:

• Геометрия:

• —    Двумерная структурированная сетка носовой части десантного модуля.

• —    Трёхмерная структурированная расчётная сетка ударного слоя.

•    Термодинамические параметры: —    Локальные концентрации всех компонентов газа в ударном слое. —    Пространственные распределения:

* поступательной температуры ( ТД,

* средней колебательной температуры молекул (Ту),

* электронной температуры ( Т'_е = Ту для молекул),

* вращательной температуры ( Tj = Tf_r для молекул).

•    Спектроскопические данные:

• —    Полный набор электронных уровней для атомов и молекул:

* для атомов и молекул — энергии электронных уровней и их статвеса.

• —    Параметры переходов:

• *    информация по всем электронно-колебательным переходам для молекулярных компонентов,

• *    информация по всем электронным переходам для атомарных компонентов.

• — Соответствующие коэффициенты Эйнштейна.

По формуле (8) были проведены расчеты лучистых потоков, суммированных по длинам волн, на каждую ячейку сетки поверхности десантного модуля на трех траекторных точках: 87 км (рис. 6), 90 км (рис. 7), 95 км (рис. 8). Были получены три картины распределения потока по поверхности десантного модуля.

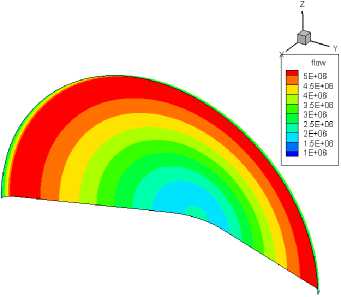
Рис. 6. Распределение лучистых потоков па высоте Н = 87 км, [Вт/м2]

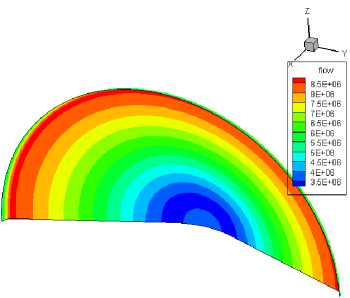
Рис. 7. Распределение лучистых потоков па высоте Н = 90 км, [Вт/м2]

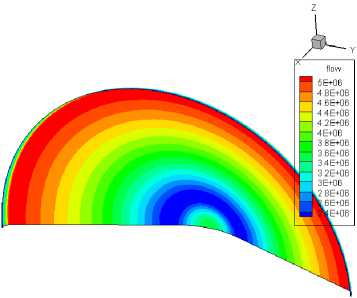
Рис. 8. Распределение лучистых потоков па высоте Н = 95 км, [Вт/м2]

В критической точке лобового щита температуры имеют локальный максимум, т.к. ударная волна является прямой. Далее, отступая от критической точки, ударная волна становится косой и температура в ударном слое падает, поэтому лучистый тепловой поток тоже падает. Однако, так как толщина ударного слоя растет к закруглению лобового щита, перед закруглением тепловой лучистый поток растёт и принимает максимальное значение, превышающее значение в критической точке.

Также если сравнивать картины распределения лучистых потоков по поверхности ДМ на всех трех траекторных точках, то можно заметить, что они имеют разную степень немонотонности. Это связано с падением скорости при уменьшении высоты и с тем, что толщина ударного слоя растёт с увеличением высоты из-за влияния вязких эффектов, одновременно также увеличивается размер зоны релаксации (колебательной температуры и концентраций компонентов).

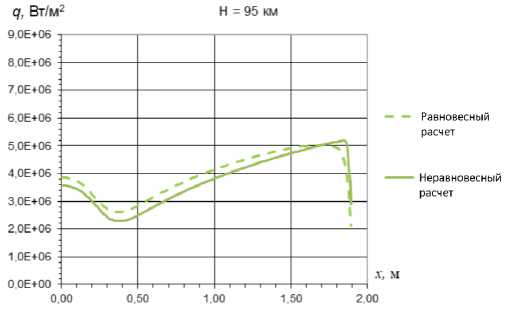
В данной работе было также рассмотрено равновесное приближение. Неравновесный расчет является более точным, так как в нем учитывается конечная скорость реакций, происходящих в ударном слое. Однако он является намного более трудоемким, чем равновесный расчет. В равновесном расчете температуры по всем степеням свободы берутся равными поступательной и для определения коэффициентов поглощения используются многогрупповые модели, усредненные по спектральным интервалам [4]. На рисунках 9, 10 и 11 представлено сравнение распределения лучистых потоков, рассчитанных в данной работе в равновесном и в неравновесном приближениях, на всех трех рассматриваемых траекторных точках (87, 90 и 95 км). Графики построены по линии симметрии поверхности спускаемого аппарата.

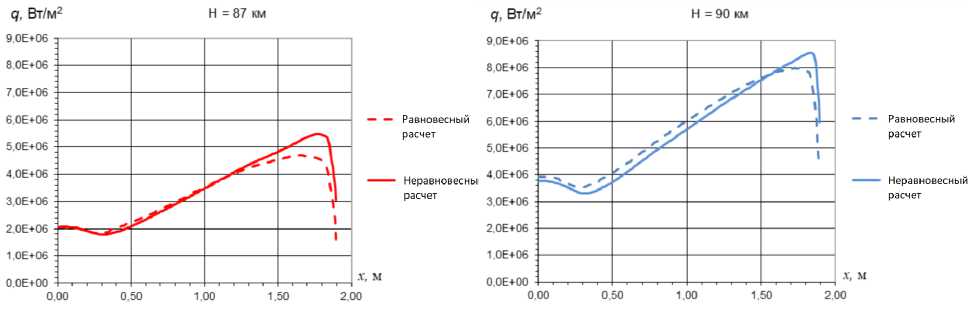
Рис. 9

Рис. 10

9. Заключение

Выполнено моделирование лучистых тепловых потоков для полной поверхности десантного модуля при входе в атмосферу Венеры в условиях термодинамического неравновесия, в отличие от предыдущих исследований, рассматривавших толвко окрестноств критической точки [9]. Результаты моделирования подтвердили, что условия атмосферы Венеры, включающие высокие температуры и давление, создают значительные термические нагрузки на спускаемый аппарат. Также было проведено сравнение равновесного и неравновесного подходов к расчету лучистых потоков в данной постановке задачи. Полученные графики демонстрируют удовлетворительную близость друг к другу для каждой траекторной точки, что позволяет рассматривать равновесную модель как физически обоснованное упрощение для данной постановки задачи, обеспечивающее значительное снижение вычислительных затрат.

Полученные результаты могут служить основой для дальнейших исследований в области аэродинамики и радиационной газовой динамики, а также способствовать разработке новых технологий для будущих космических миссий на Венеру.