Численное моделирование механоэлектрической обратной связи в деформированном миокарде

Нарушение сердечного ритма является одним из самых распространенных сердечно-сосудистых заболеваний. Изучение причин возникновения этого опасного состояния может способствовать его своевременному предупреждению и лечению.

С макроскопической точки зрения сердечная мышца может рассматриваться как две проводящие среды, заполняющие внеклеточное и внутриклеточное пространство и взаимодействующие через мембрану. Благодаря волокнисто-слоистой организации сердечная ткань обладает значительной анизотропией. Значения проводимости в разных направлениях различаются на порядок [1]. Целостность внутриклеточного пространства как проводящей среды обеспечивается щелевыми соединениями.

Электрическая стимуляция запускает рост концентрации ионов кальция в сердечной клетке, что в свою очередь приводит к сокращению сердечной мышцы (электромеханическое сопряжение). Сопровождающие работу сердца большие деформации оказывают сильное воздействие на процесс электрического возбуждения (возникает механоэлектрическая обратная связь). Можно выделить следующие типы механоэлектрической обратной связи: изменение проводимости миокарда; возникновение дополнительных трансмембранных токов (активируемых деформацией ионных каналах).

К механоэлектрической обратной связи тесно примыкает влияние деформации на сократительный аппарат мышечной клетки. Этот тип механочувствительности обеспечивается следующими клеточными процессами: изменением размера перекрытия между тонкими и толстыми филаментами в саркомере; изменением чувствительности сократительного аппарата к ионам кальция; переходом, связанным с освобождением и захватом ионов кальция в саркомере. Первые два процесса совершаются быстро и оказывают влияние на сокращение миокарда в течение сердечного цикла. Третий процесс относится к медленным и отражается на режиме сокращений в последующих циклах [2]. Первые два процесса представлены в большинстве моделей электромеханического сопряжения [3–6]. Влияние кинетики ионов кальция можно найти в работах [7, 8]. Поскольку механочувствительность тесно связана с процессом электромеханического сопряжения и учитывается в соответствующих моделях, в основной части данной работы она не будет рассматриваться.

При исследовании проводимости деформируемой сердечной ткани возможны два подхода [9]: в одном (наиболее распространенном) миокард полагается анизотропной жидкостью, в которой проводимость в направлении любой из материальных осей не зависит от деформации, происходит только поворот тензора проводимости вместе с материальными осями. Во втором подходе миокард представляется как пространственная решетка резисторов, для которой сопротивление между любыми двумя точками не меняется при деформации. Каждому из этих подходов соответствует свой носитель: у первого — это цитоплазма, у второго — щелевые соединения. В книге F.B. Sachse [9] предложен подход, включающий оба типа носителя, при этом вводится некоторый параметр, изменяющийся в пределах от нуля до единицы, и его крайние значения соответствуют этим случаям.

В представляемой работе используется модель изменения внутриклеточной проводимости миокарда при его деформации, построенная на основе микроструктурной модели из работы [10]. В упомянутой модели сердечная ткань имеет вид периодической решетки, где клетки являются прямоугольными призмами, заполненными изотропной проводящей жидкостью, а проводимость щелевых соединений учитывается через граничные условия на сторонах призм. Далее с помощью метода гомогенизации и вычисления общего тока через периодическую структуру значения внутриклеточной проводимости вдоль и поперек волокна выражаются через размеры клетки, параметры периодичности решетки, электрические свойства миоплазмы и щелевых соединений. Кроме того, в [10] показано, что внеклеточная проводимость слабо зависит от самих линейных размеров клетки и обусловливается в основном отношением размеров клетки к соответствующим параметрам периодичности структуры (долей внеклеточного пространства). Поэтому следует ожидать, что внеклеточная проводимость почти не связана с деформациями.

Если деформация миокарда в материальных осях представляет собой растяжение–сжатие, то зависимость макропроводимостей от деформации может быть получена с помощью довольно простых обобщений модели из [10], учитывающих слоистую структуру миокарда при подстановке измененных размеров в выражения для внутриклеточной проводимости. Для более общего случая, когда главные оси деформации не совпадают с материальными осями, связанными с волокнисто-слоистой структурой миокарда, при рассмотрении миокарда в этих материальных осях в нем присутствуют сдвиги. Аналитическое решение на основе модели [10] также может быть получено, но только при использовании метода гомогенизации в виде, представленном в работе [11].

При выводе зависимостей проводимостей от деформации были сделаны следующие предположения: цитоплазма представляет собой изотропный электролит с удельной проводимостью, не зависящей от деформации; проводимости щелевых соединений постоянны; деформация клетки тождественна деформации среды. Эта модель может быть обобщена с целью учета анизотропии миоплазмы, связанной с ее микроструктурой. Подробно вывод зависимости проводимости от деформации приведен в работах [12, 13].

В деформируемом миокарде могут активироваться трансмембранные каналы и, как следствие, возникать дополнительные источники электрического возбуждения, что может повлечь за собой сердечную аритмию. Существует большое число каналов, разнообразных по механизмам передачи нагрузки друг другу и реакции на нее [2, 14–16]. Разработанные в настоящее время модели в недостаточной мере учитывают пространственный характер деформации. Как правило, активация каналов зависит от их удлинения в направлении волокна, что для быстро активируемых деформацией каналов, расположенных на мембране мышечной клетки, не очевидно.

В данной работе построена модель активации каналов при сложном деформировании при следующих предположениях: каналы равномерно распределены по боковой поверхности клетки; каналы реагируют на локальное увеличение площади участка мембраны [17, 18]; формула, в которой используется удлинение вдоль волокна, верна для случая одномерного растяжения в этом направлении.

• 2.    Миокард как проводящая среда

С макроскопической точки зрения сердечная мышца может рассматриваться как две неоднородные анизотропные проводящие среды — внеклеточная и внутриклеточная, которые заполняют пространства, взаимодействующие через мембрану. Каждая из этих двух сред характеризуется своим тензором проводимости. Построенная на этих предположениях модель называется бидоменной и имеет вид [1]

• V .( D^ Vm ) + V.( D^ Ve ) = xIm + x Its + Is ,(1)

• V .(( D + De )V Ve ) + V.( D,V Vm ) = I„ + I»(2)

при граничных условиях n .(D V Ve ) = -n .(D V Vm ) ,(3)

n .(De V Ve ) = 0.(4)

Здесь: V и V e — внутриклеточный и внеклеточный потенциалы; V_m = V - V_e — трансмембранный потенциал; D и D_e — внутриклеточный и внеклеточный тензоры проводимости; I_m — трансмембранный ток; х — площадь клеточной мембраны на единицу объема; I s — трансмембранный источник тока, связанный, например, с действием активируемых деформацией каналов; I s и I_es — внешние источники тока, подводимого к внутриклеточной и внеклеточной средам, соответственно; n — вектор нормали к клеточной мембране.

Трансмембранный ток может быть представлен как сумма емкостного тока, пропорционального скорости изменения трансмембранного потенциала, и тока I _on , обусловленного движением ионов через мембрану:

I m = C m dd T + ^^O n ( V m ’ Г ) ' (5)

Здесь: C_m — емкость клеточной мембраны; r — вектор внутренних переменных, изменение которых во времени t описывается системой дифференциальных уравнений вида:

^ - R ( Vm , Г ) = 0.(6)

Если предположить, что тензоры проводимости внутриклеточного и внеклеточного пространств подобны:

De =AD„ то модель сердечной мышцы значительно упрощается и преобразуется к виду

• V .( Dm V Vm )=X Im + XIB + 4(8)

при граничных условиях

П ■(Dm V Vm ) = 0.(9)

Такая модель называется монодоменной, здесь D m = ( а/( 1 + Л ) ) D i — ее приведенный тензор проводимости.

В случае изотропной среды, для которой условие подобия вне- и внутриклеточного пространств выполняется автоматически, результаты, полученные с помощью бидоменной и монодоменной моделей, в точности совпадают. Что касается анизотропных моделей сердечной ткани, то для них, при надлежащем выборе параметров, результаты, описывающие распространение волны возбуждения, различаются незначительно [18]. В данной работе проводимости монодоменой модели в материальных осях будут вычисляться, согласно [18], как среднее гармоническое соответствующих внутриклеточных и внеклеточных проводимостей:

^ m =C i G e K^Ci ^+C e ) "                                         ⁽¹⁰⁾

Однако бидоменная модель становится необходимой в тех случаях, когда принимается во внимание сам процесс возбуждения от внешних факторов и/или когда требуется сравнение с реально измеренным внеклеточным потенциалом [19]. Обзор таких проблем можно найти в [20, 21]. Одним из наиболее ярких примеров, в котором бидоменная модель себя проявляет, — это образование виртуальных электродов [22]. Оказывается, что при подведении к миокарду электрического тока в малой области вокруг электрода могут формироваться области деполяризации и гиперполяризации. Их появление, с одной стороны, может приводить к возбуждению спиральных волн [23], а с другой, — может быть использовано в процессе дефибрилляции [24, 25]. Что характерно, виртуальные электроды возникают только в том случае, когда условие подобия (7) не выполняется. При этом для исследования процесса развития возбуждения необходимо решать полную систему (1)–(6). Однако при малой силе возбуждающего тока для определения первоначальной конфигурации виртуальных электродов достаточно решения линеаризованной статической бидоменной задачи:

V. ( D ? V m ) + V- ( D ^ V_e ) = X G 0 V m +x I ts + I s ,                         (11)

V. ( ( D i + D e ) V V e ) + V. ( D V V m ) = I s + I s •                            (12)

Здесь:    V m = V m - V_rest   — отклонение трансмембранного потенциала от потенциала покоя;

G ₀ = ( d l ion /д V m )    — линеаризованная в окрестности потенциала покоя проводимость мембраны.

V V rest

При выполнении соотношения (7) задача (11), (12) становится вырожденной:

V. ( D m V V m ) =X G 0 V m +X I_G +^

| ][ is

1 + Л J

¹ । a es . 1 + Л J

Уравнение (13) не демонстрирует возникновение виртуальных электродов, но имеет аналитическое решение [26] и может быть использовано при проверке адекватности конечно-элементных программ.

• 3.    Проводимость деформированного миокарда

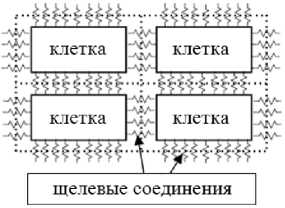
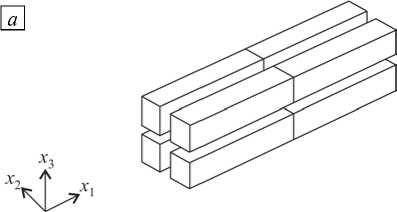
Вывод макропроводимостей проводился на основе микроструктурной модели [10]. В этой работе сердечная ткань рассматривалась как периодическая решетка, где клетки являются прямоугольными призмами, заполненными изотропной проводящей средой, а проводимость щелевых соединений учитывалась через граничные условия на сторонах этих призм (Рис. 1). Считалось, что в направлении волокна клетки прилегают друг к другу, в поперечных направлениях между ними существуют промежутки. Значения внутриклеточной проводимости вдоль и поперек волокна выражались через размеры клетки, параметры периодичности решетки, электрические свойства миоплазмы и щелевых соединений с помощью метода гомогенизации и вычислении величины общего тока через периодическую структуру.

б

Рис. 1. Периодическая клеточная структура миокарда в материальных осях: общая схема ( а ), пространственное расположение ( б )

В [10] также показано, что внеклеточная проводимость слабо зависит от самих линейных размеров клетки и определяется в основном отношением размеров клетки к соответствующим параметрам периодичности структуры (то есть долей внеклеточного пространства). Поэтому следует ожидать, что внеклеточная проводимость будет слабо обусловливаться деформацией.

Если в материальных осях деформация представляет собой растяжение–сжатие, то зависимость макропроводимостей от деформации может быть получена с помощью довольно простых обобщений модели, в которых учитывается слоистая структура: разные в 2-х поперечных направлениях проводимости щелевых соединений, размеры клетки и параметры периодичности. При выводе зависимости проводимостей от деформации в этом случае принимаются следующие предположения:

• - цитоплазма есть изотропный электролит с удельной проводимостью ст с , не зависящей от деформации;

  – проводимости щелевых соединений постоянны;

  – деформация клетки, деформация внеклеточного пространства и деформация среды одинаковы.

Применение к этим уравнениям (по аналогии с работой [10]) метода гомогенизации, а также вычисление общего электрического тока через периодическую структуру в направлениях материальных осей x 1 , x ₂ и x ₃ приводит к следующим соотношениям для макропроводимостей в соответствующих направлениях:

w c 2 w c 3 С ¹

°1 = ° c---------I 1 —;----- wp 2 wp 3 I   1 + K1

w c 3 I 1

°2 = °c ----I 1 — wp 3 (

^{1 +} h_c 2 ^K 2

„         wc 2 I ,

° 3    ° c      I ¹

w p 2 (

—

^{1 +} h c 3 ^K 3

Здесь: h_{c 2} = w_{c 2}/ l ; h_{c 3} = w_{c 3} /I ; K 1 = ( g 1 l )/( ° _cw_{c 2} w_{c 3} ) ; k ₂ = g ₂ /( ° _cw_{c 3} ) ; k ₃ = g ₃ /( ° _cw ₂ ) ; l — длина клетки; w c ₂ , w c ₃ — поперечные размеры клетки; w_{p 2} , w_{p 3} — параметры периодичности решетки; g 1 , g ₂ , g ₃ — полные проводимости щелевых соединений на соответствующих сторонах призм, моделирующих клетки.

Подставив в соотношения (14) размеры клетки, изменившиеся в процессе деформации:

l = L X 1 ,     w_{c 2} = W_{c 2}Х₂ ,    w_{c 3} = W_{c 3} X ₃ ,

где L , W_{c 2} , W_{c 3} — первоначальные размеры, X 1 , X ₂ , Х ₃ — удлинения ткани в материальных осях, получаем искомые зависимости макропроводимостей:

° 1

.XA'

-   + -0 л

° c 1    ° g 1     ^X 1 р

° 2

I 1      1    X 1 X ₃ '

-   + ~0 'л

(° c 2    ° g 2    ^X 2 J

° 3

I 1      1    X 1 X ₂ '

-   + ~0 ' л

₍ ° c 3    ° g 3    ^X 3 р

.

Здесь ° gi — проводимости щелевых соединений, ° g

— их значения в недеформированном состоянии.

б

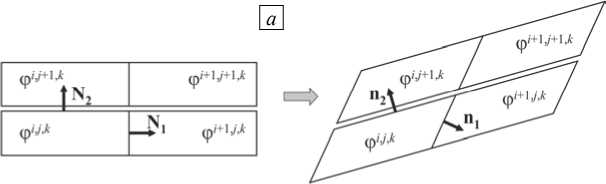
Рис. 2. Общий вид периодической клеточной структуры недеформированного и деформированного миокарда

В более общем случае, когда главные оси деформации не совпадают с материальными осями, связанными с волокнисто-слоистой структурой миокарда, в миокарде присутствуют сдвиги относительно материальных осей. В результате периодическая структура, которая в недеформированном состоянии была прямоугольной, при деформировании становится косоугольной (Рис. 2). Нормали в отсчетной ( N j ) и текущей ( n j ) конфигурациях связаны как n j da = J F ^-T ' N j dA (формула Нансона), соответствующие удельные проводимости щелевых соединений, приведенные к поверхности, — как у j da = Г j dA . Здесь F — тензор градиента деформации.

С учетом сказанного уравнения проводимости для периодической структуры запишутся как [12]

—°cУф1’j’k (l, x2, x3)' П1 = Y1 (ф*’j’k (l, x2, x3) — Ф*+1,j’k (0, x2, x3)),(17)

—°c Уф1’j’k (x,, Wc2, x3)' n2 = Y2 (ф1’j’k (x), Wc2, x3) — ф1,j+1,k (x1,0, x3)),(18)

—°cVф1,j,k (x1, x2, Wc3)' П3 = Y3 (ф1,j,k (x1, x2, Wc3) — ф1,j,k+1 (x1, x2,0)),(19)

(Уф1-j• k (l, x2, x3) — Уф141-7-k (0, x2, x3))' n1 = 0,(20)

(Уф1'j'k (x1, Wc2, x3) — Уф1'j+1,k (x1,0, x3))' n = 0 ,(21)

(Уф1’7’k (x1, x2, Wc3) — Уф1’7’k+1 (x1, x2,0))' n3 = 0 ,(22)

где ф ¹ ’ j ’ k — внутриклеточный потенциал ( i , j ) клетки на слое k .

Подставляя в (17)–(22) формулу Нансона, соотношения для проводимостей щелевых соединений в недеформированном и деформированном состояниях и применяя метод гомогенизации в виде, предложенном в работе [11], можно получить формулу для вычисления тензора макропроводимостей [12]:

^ c^Vc         С^-1 /Г- 1   - 1

d ik = у  ⁽⁵ ik + F ji M jl F Ik ) ,                                            ⁽²³⁾

Vp где Vc — объем клетки, Vp — объем ячейки периодичности, 5ij — символ Кронекера,

	- C 111 -к 1	-C - 1 12	-C -1 Л 13
M =	- 1 21	- C 221 -к 2	-C - 1 23	.                                       (24)
	-C - 1 ^     ^31	-C - 1 32	- C 3 - 31 -к 3 ?

Здесь: к i = ( Г i l )/( о _CJ ) ; к 1 =к 1 , к ₂ = h c ₂ к ₂ , к ₃ = h c ₃ к ₃ ; C — тензор меры деформации Коши-Грина.

В формуле (24) C i - ¹ означает ij -ю компоненту тензора C ^{- 1}, а не величину, обратную C ij .

В матричном виде тензор макропроводимостей может быть представлен как тензор, обратный сумме обратных тензоров проводимости цитоплазмы и щелевых соединений:

d-1 = 0, (d-1 + d1), где

d c =^ c I, d g =° C Fd g 0FT являются приведенными тензорами проводимости цитоплазмы и щелевых соединений, dg0 — тензор проводимости щелевых соединений в недеформированном состоянии.

Соотношения (23)–(27) выводились при предположении изотропии проводимости миоплазмы. Анизотропия проводимости миокарда в этом случае является результатом только сопротивления щелевых соединений. Однако, благодаря внутренней структуре клетки, содержащей параллельные нитевидные структуры — миофибриллы, эффективная проводимость самой миоплазмы может быть анизотропной. Рассматриваемая модель может быть обобщена с целью учета анизотропии миоплазмы, если в ней заменить (43) на выражение:

d _c = R d 0 R ^T.

Здесь d⁰ — тензор проводимости цитоплазмы в начальных осях, R — матрица поворота осей анизотропии.

Подробно вывод зависимости проводимости от деформации приведен в работах [12, 13].

• 4.    Активируемые деформацией каналы

При деформировании миокарда в нем могут активироваться трансмембранные каналы и, как следствие, возникать дополнительные источники электрического возбуждения, что может вызвать сердечную аритмию. Существует большое число каналов, разнообразных по механизмам передачи им нагрузки от ткани и реакции на нагрузку. Разработанные в настоящее время модели в недостаточной мере учитывают пространственный характер деформации. В них, как правило, активация каналов зависит от удлинения в направлении волокна, что для быстро активируемых деформацией каналов, расположенных на мембране мышечной клетки, не очевидно.

Активируемый деформацией ток I_SAC вычисляется как произведение зависящей от деформации функции активации L ( X ) , проводимости активируемых деформацией каналов G SAC и разности между трансмембранным потенциалом V и обратным потенциалом V_r [16]:

I sac = L ( X ) G sac ( V - V_r ) .

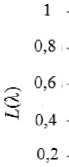
о

О 0,5        1         1,5        2

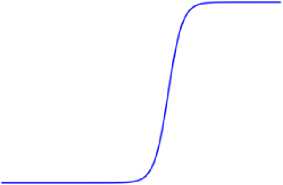
Рис. 3. Общий вид функции активации

Значения G_SAC и V_r индивидуальны для каждого типа канала. Функция активация имеет область значений в интервале от нуля до единицы, а в случае сжатия равна нулю. Общий вид этой функции показан на рисунке 3, а далее приводится пример ее записи:

L ( ^X ) =

1 + exp ( ^- a ( ^X-X m ) ) ,

не так. В данной работе исследуется

где а и X _m — эмпирические параметры.

При деформации клетки вдоль волокон все каналы, располагающиеся на ее боковой поверхности, находятся в равных условиях; при произвольной деформации это возможность обобщения потенциала (28) для сложного

деформирования при следующих предположениях:

– каналы равномерно распределены по боковой поверхности клетки;

– каналы реагируют на локальное увеличение площади участка мембраны [17, 18];

– формула, в которой используется удлинение вдоль волокна, верна при одномерном растяжении вдоль

волокна.

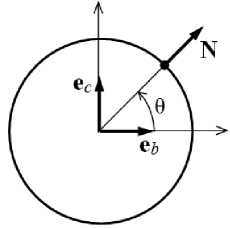
Рассмотрим фрагмент мышечной клетки в материальных осях, представленный, как цилиндр, ориентированный вдоль направления волокна (Рис. 4). Здесь ось a направлена вдоль волокна; b — в плоскости, касательной мышечному слою, перпендикулярно волокну; c — перпендикулярно слою. Тогда нормаль N в произвольной точке боковой цилиндрической поверхности мышечного волокна выразится как

N = e b cos 9 + e c sin 9 .

Здесь: e _b , e _c — орты осей b и c ; 9 — угол между нормалью и e _b .

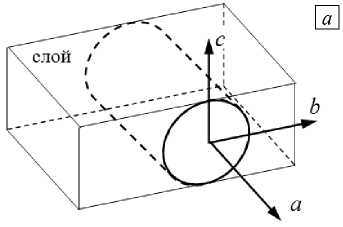
Рис. 4. Фрагмент мышечного волокна (клетки): положение материальных осей ( а ) и нормали к боковой поверхности в поперечном сечении ( б )

б

С помощью формулы Нансона можно определить локальное изменение площади мембраны:

J = da = J F - T - N = J N - F ^{- 1} F ^{- T} - N = JJ N - C ^{- 1} - N .

^A dA           ²

Подставляя (29) в (30), получаем зависимость локального изменения площади мембраны от компонент тензора меры деформации Коши–Грина в осях a , b и c :

J = da = J Jr ^{- 1} cos² 9 + C ^{- 1} sin² 9 + 2 C "1 cos 9 sin 9 = C cos² 9 + | C sin² 9 + 2 | C cos 9 sin 9 =

A dA           bb              cc                bc                        bb                 _cc                  b _c

= V( C aa C cc - ^C« ) cos² 9 + ( C aa C bb - C c ) sin² 9 + 2 ( C ^b C ^c - C_aaC bc ) cos 9 sin 9 .

Здесь: x = a , b , c ; y = a , b , c ; C xy и C - — компоненты тензоров C и C ¹ в материальных осях; | C| — соответствующие алгебраические дополнения матрицы тензора C .

Рассмотрим одноосное растяжение X вдоль волокна: X a = X , X b = X c = X ^0,5. В этом случае тензор меры деформации Коши–Грина имеет вид:

^Xa 0 0 Л x2 0 01 C = 0 X 2 0 = 0 X-1 0 10 0 X2, 10 0 X-1 а локальное изменение площади мембраны постоянно и равно

J. = da = VX 2 X^{- 1} cos² 9 + X 2 X^{- 1} sin² 9 = X ^0,5.                              (32)

A dA

Таким образом, в (28) можно заменить L ( X ) на L ( J ² ) .

При произвольном деформировании локальное изменение площади мембраны J_A зависит от координаты 9 . Тогда вместо (28) нужно использовать формулу, являющуюся результатом осреднения L ( J A ) по угловой координате 9 :

I sac = L ( C ) G sac ( V - V_r ) ,

где

^{2 п}

L ( C ) = — J l ( J A ( C , 9 ) ) d 9 ,                                  (34)

^{2 n} 0

а J_A ( C , 9 ) вычисляется согласно (31). В качестве L ( J A ) используется функция L ( X ) из (28).

• 5.    Результаты

Для одноосного растяжения проведено сравнение результатов, полученных по модели, принятой автором, и по модели, предложенной в [9]. На рисунке 5 показано изменение параметра q — отношения продольной внутриклеточной проводимости при растяжении вдоль волокна к продольной внутриклеточной проводимости недеформированного миокарда. Видно, что обе модели хорошо согласуются при удлинениях в интервале от 0,8 до 1,2 (в области, выделенной на рисунке серым цветом). Для поперечной проводимости имеет место доминирование щелевых соединений.

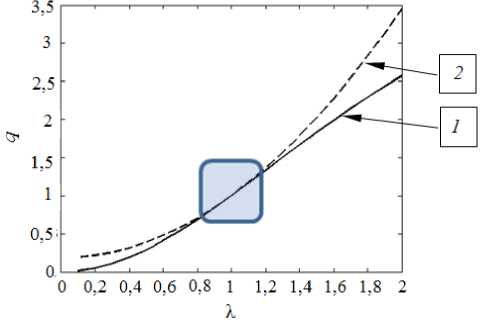
Рис. 5. К сравнению моделей проводимости деформированного миокарда: кривая 1 отвечает модели, принятой автором данной работы, 2 – модели из книги Sachse [9]

Было исследовано распространение волны возбуждения в прямоугольной области при удлинении X = 1,4 вдоль горизонтальной оси, соответствующей направлению волокна. Источник первоначального возбуждения располагался в середине левой границы прямоугольной области. В задаче решалась монодоменная система (6), (8) при граничных условиях (9) с помощью численного алгоритма, основанного на методе расщепления [1] и программно реализованного на базе конечно-элементной библиотеки

Таблица 1. Продольная проводимость при деформации

Вид модели	Тип проводимости
	внутриклеточная	приведенная согласно монодоменой модели
Решетка резисторов	1,96	1,24
Модель, принятая автором	1,24	1,09

FEniCS [27]. Результаты показаны в таблице 1, где даны отношения проводимости деформированной и недеформированной сердечной ткани, и на рисунке 6. Влияние деформации оказывается сильно «разбавленным» внеклеточной проводимостью. В силу этого представленные на рисунке 6 результаты моделирования демонстрируют незначительные отличия.

Рис. 6. Распространение волны возбуждения в прямоугольной области, заполненной возбудимой средой как квазижидкость ( а ), решетка резисторов ( б ), согласно модели, принятой автором ( в )

Следующий пример иллюстрирует более тонкие эффекты. Рассматривалось возникновение областей деполяризации и гиперполяризации (образование виртуальных электродов) при точечном катодном возбуждении внеклеточной среды в двумерной прямоугольной области. Это явление имеет место в том случае, когда условие подобия (7) не выполняется, что характерно для реального миокарда. Тензор внеклеточной проводимости близок к шаровому, а компоненты тензора внутриклеточной проводимости могут отличаться на порядок. В качестве меры отклонения этих тензоров для двумерных задач может быть использован параметр из [28], равный нулю при условии, что тензоры внутриклеточной (индекс i ) и внеклеточной (индекс e ) проводимостей двух сред подобны:

e = 1 -

⁽ ° e, /° ey ) К К )

Точное решение этой задачи может быть получено только тогда, когда тензоры вне- и внутриклеточной проводимости подобны, то есть при отсутствии виртуальных электродов [29]. Вследствие этого для оценки влияния деформации на конфигурацию виртуальных электродов использовано приближенное решение [8]. Значения параметра e , вычисленные при различных зависимостях проводимости от деформации, приведены в таблице 2. Соответствующие конфигурации виртуальных электродов показаны на рисунке 7. Влияние деформации в присутствии виртуальных электродов оказывается более значительным.

Таблица 2. Изменение параметра отклонения от подобия при деформации

Квазижидкость	Решетка резисторов	Модель, принятая автором
0,596	0,853	0,768

Рассмотрено также возникновение активируемых деформацией токов при одноосном растяжении X поперек волокна (в направлении оси b ). В этом случае тензор меры деформации Коши–Грина имеет вид:

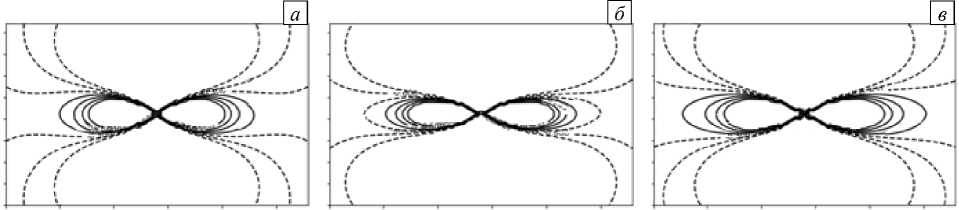
Рис. 7. Виртуальные электроды при точечном катодном возбуждении в области с возбудимой средой, рассматриваемой как: квазижидкость ( а ), решетка резисторов ( б ), согласно данной модели ( в ); сплошные линии соответствуют областям деполяризации, штриховые – областям гиперполяризации

fx^{- 1}

к

C = 0

X ²

к

х^{- 1}

/

а локальное изменение площади мембраны, согласно (48), следующее:

J A ( 9 ) = X^{- 1} X^{- 1} cos² 9 + X^{- 1} X ² sin² 9 = X^{- 2} cos² 9 + X sin² 9 .

На рисунке 8 показаны распределения по угловой координате локального изменения площади межклеточной мембраны и соответствующих значений функции активации при использовании функции активации вида, представленного на рисунке 3. Видно, что значительная часть мембраны находится в состоянии сжатия, и поэтому большая часть каналов не активирована. В этом случае отношение активируемых деформацией токов I_{SAC , b} и I_{SAC , a} при растяжении поперек и вдоль волокна равно:

Г = I SAC , b^SAC , a = L b/ L a = 0,3531.

Здесь L_a и L b — значения L ( C ) при растяжении миокарда, соответственно, вдоль и поперек волокон.

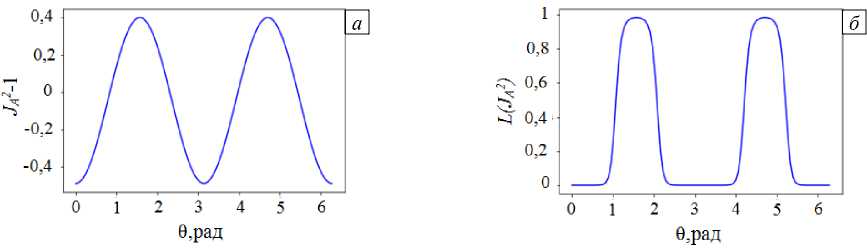
Рис. 8. Распределения по угловой координате в активируемых деформацией каналах при поперечном растяжении локального изменения площади мембраны ( а ), функции активации ( б )

• 6.    Заключение

Выделены следующие типы механоэлектрической обратной связи: изменение проводимости миокарда и возникновение дополнительных трансмембранных токов (активируемые деформацией ионные каналы).

Тензор внутриклеточной проводимости может быть представлен как тензор, обратный сумме обратных тензоров проводимости цитоплазмы и щелевых соединений. При исследовании распространения волны возбуждения влияние деформации оказывается сильно «разбавленным» внеклеточной проводимостью. При исследовании более тонких эффектов, таких, например, как образование виртуальных электродов (когда внеклеточная и внутриклеточная среды выступают более индивидуально), влияние деформации сказывается сильнее.

Построена модель активации каналов в условиях сложного деформирования при следующих предположениях: каналы равномерно распределены по поверхности клетки; каналы реагируют на локальное увеличение площади участка межклеточной мембраны; формула, в которой используется удлинение вдоль волокна, верна для одномерного растяжения вдоль волокна. Эта модель позволяет рассматривать активацию каналов не только при растяжении вдоль волокна, но и в произвольном направлении.

Более детальное моделирование связи механических и электрических процессов дает возможность глубже вникнуть в причины возникновения нарушений ритма сердца и способствует своевременному предупреждению и лечению этих опасных для человека состояний.

Исследование выполнено при финансовой поддержке РФФИ и Пермского края в рамках научного проекта № 19-41-590002 р_а.