Численное моделирование миграции фильтрационных вод от объектов размещения твердых коммунальных отходов через грунтовые защитные сооружения

Одним из самых важных негативных воздействий объектов размещения отходов на окружающую среду является попадание образующихся в них фильтрационных вод (фильтрата) в подземные и поверхностные воды и грунтовый массив их основания. Фильтрат определяется как высокотоксичная жидкость, включающая в себя тяжелые металлы, органические загрязнители, аммиачный азот и иные компоненты [1 –4] . Он образуется при взаимодействии отходов с просачивающимися в тело полигона атмосферными осадками [5] . Поэтому актуальны различные способы, во-первых, сбора стоков и обработки перед сбросом в водоем, канализационную систему, на полигон или свалку, во-вторых, предотвращения попадания фильтрата за пределы рабочего тела массива отходов. В [6] проведен обзор современных технологий очистки фильтрата. Рассмотрены разные виды обработки этой жидкости, включая биологические и физико-химические методы, а также их комбинации [7 –9] . Сделан вывод, что отдельные биологические или физико-химические методы не могут обеспечить удовлетворительную эффективность очистки фильтрата. Максимальный эффект очистки достигается при использовании комбинации двух или более физикохимических обработок, а также при комбинации биологического и физико-химического способов.

Эффективным способом снижения вредного воздействия на экологию загрязненных фильтрационных вод служит их рециркуляция — вторичное использование в качестве сырьевых ресурсов. При рециркуляции фильтрата снижается общий объем токсичной жидкости за счет, например, ее испарения [10] . Работа [11] знакомит с технологией утилизации фильтрата методом перевода его в твердый продукт — литификат, который приобретает сорбционные свойства. В [12, 13] рассмотрены различные технологии очистки свалочного фильтрата посредством мембранных технологий, методов электрохимии и другого.

Обнаружение путей миграции свалочного фильтрата представляется очень важным. Создание для этих целей математических моделей и их применение — один из способов решения этой проблемы. Моделирование таких систем, как полигоны твердых коммунальных отходов (ТКО), является сложной задачей. Трудности обусловлены рядом неопределенностей, связанных с оценкой параметров модели, которая должна адекватно

Статья опубликована в открытом доступе по лицензии CC BY 4.0

изображать биологические, химические и физические процессы, происходящие на свалках. Для проверки предлагаемых моделей требуется большое количество полевых данных. В [14] осуществлен обзор математических моделей, предназначенных для имитации образования и распространения фильтрата на полигонах ТКО, а также обсуждаются будущие потребности и потенциальные улучшения существующих моделей.

В работах [15, 16] изучались процессы миграции загрязняющих веществ от полигона ТКО, расположенного в водоохранной зоне озера Селигер (Тверская область, Российская Федерация). Для определения параметров математического моделирования проводились полевые и лабораторные исследования в районе расположения свалки. Предложены модели, которые описывают физико-химические процессы миграции веществ в почвогрунтовой толще. Результаты вычислительных экспериментов и аналитических расчетов согласуются с натурными данными, что дало основание рекомендовать предлагаемые математические модели для прогнозирования миграции загрязнений от полигона.

Для изучения последствий воздействия человека на окружающую среду разработаны различные программные продукты. Моделирование инфильтрации образующейся свалочной жидкой субстанции через наслоения отходов с учетом природно-климатических условий на полигоне «Новые Черкассы» (г. Уфа, Российская Федерация) выполнена в [17] с использованием программы HELP [18] . Там же осуществлена имитация движения загрязненной жидкости, которая просачивается в подстилающий грунт, с помощью программы HYDRUS [19] . Результаты моделирования на основе данных за 10 лет выявили, что на полигоне образуется повышенное количество фильтрата, обусловленное возрастом полигона и отсутствием защитных мер по предотвращению инфильтрации загрязненной жидкости в почву. Расчеты показали, что за период эксплуатации полигона «Новые Черкассы» токсичные массы распространились за его пределы более чем на 7 км.

Стоит отметить, что не только свалки ТКО представляют опасность для гидросферы и здоровья человека, но и объекты размещения отходов производства. Так, в работе [20] с помощью пакета ANSYS Fluent проведено прямое трехмерное моделирование процесса инфильтрации высококонцентрированных рассолов из хранилища жидких отходов, находящегося в Верхнекамском месторождении калийных и магниевых солей (Пермский край, Российская Федерация), в окружающую породу. Разработанный комплекс физических моделей достоверно описывает гидродинамические процессы, связанные с эксплуатацией крупного хранилища, и может быть успешно применен для прогнозирования положения границ загрязнения грунтовых вод в прилегающих к хранилищам породах. Пакет ANSYS Fluent также успешно применяется для моделирования потоков вулканической лавы, которые могут иметь катастрофические последствия как для окружающей среды, так и для жизни человека [21] .

Имеющиеся численные и математические модели распространения фильтрата строятся, как правило, в рамках двумерного подхода с учетом динамики загрязнения по горизонтальным направлениям. Движение фильтрата в толщу грунтовых пород по трем направлениям выполняется в рамках либо модельных, либо лабораторных ситуаций. В настоящей работе исследовалась миграция фильтрата через защитные сооружения старой свалки, функционирующей более трех десятков лет. Основным природоохранным сооружением, препятствующим прониканию фильтрационных вод за пределы объекта размещения ТКО является противофильтрационная дамба. Подобные дамбы полигонов ТКО во время эксплуатации периодически ремонтируются и восстанавливаются, поскольку происходит их разрушение в силу естественных причин. Дамба рассматриваемого полигона восстановлена в 2017 году. Для прогнозного моделирования миграции фильтрационных вод использованы данные натурных измерений, проведенных в 2017 году.

• 2.    Характеристики полигона ТКО

Исследуемый полигон эксплуатируется более тридцати лет. На его территории ежегодно производится анализ компонентов окружающей природной среды в рамках программы экологического мониторинга за качеством атмосферного воздуха, почвы, подземных и поверхностных вод, радиационного излучения. Полигон располагается на склоне водораздела, обращенном в сторону малой реки, протекающей в 300 м от него на северо-востоке. Склон имеет общий уклон в северо-восточном направлении, то есть к пойме реки. По периметру полигон окружен осушительной траншеей глубиной до 2 м и обвалован защитной дамбой трапецевидной формы с параметрами: высота до 6 м, ширина основания до 12 м. На дамбе местами присутствуют следы временных водотоков. Фильтрат с полигона растекается по противофильтрационному основанию и скапливается в двух понижениях: прудах-отстойниках. Пруд-отстойник с фильтратом, расположенный с северо-западной стороны находится в контакте с телом полигона только с одной стороны, с других сторон его берега образует защитная дамба. Прилегающая к дамбе территория представляет собой неровную, холмистую поверхность, поросшую луговой растительностью, кустарником, мелколиственными породами деревьев. В северной части, за дамбой и осушительной траншеей наблюдаются переувлажненные участки. С северо-западной стороны от дамбы на расстоянии 13 м находится озеро. Изыскания показали, что появление понижений связано как с обильными осадками, так и с притоком по основанию дамбы и под ним жидкости с площадки с отходами. В связи с этим возникло предположение о возможном распространении фильтрата из пруда-отстойника.

На рисунке 1 изображен геологический профиль рассматриваемого участка (вертикальное сечение от поверхности в глубину с изображением подстилающих пород и порядка их напластования). Координаты основных точек приведены в системе отсчета, начало которой расположено у основания дамбы со стороны пруда-отстойника. Расчетная область имеет линейный размер 10 м в горизонтальном направлении и 23 м в вертикальном.

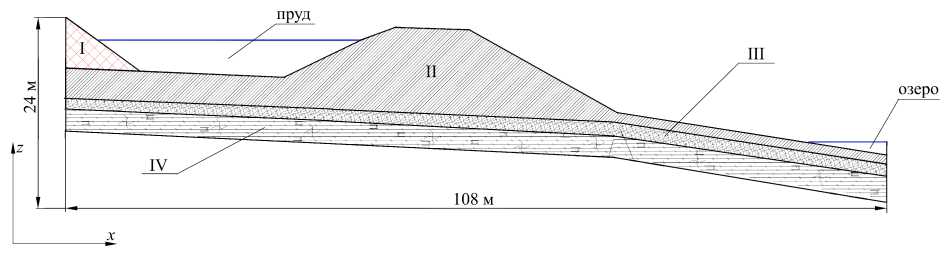
Рис. 1. Расчетная область – вертикальное сечение участка, содержащего часть насыпного грунта, пруд-отстойник, дамбу и озеро (сечение проходит через середину пруда–отстойника); на геологическом разрезе площадки полигона показаны присутствующие породы: I – насыпной грунт, II – суглинок, III – алевролит, IV – аргиллит

Как видно из рисунка, основание площадки полигона ТКО до первого водоупорного горизонта представляет сложение из трех слоев горных пород: суглинка, алевролита и аргиллита. Суглинок — дисперсная связная осадочная порода, состоящая преимущественно из песчаных и пылеватых частиц со значительным содержанием глинистых частиц, концентрация которых определяет свойства породы. Мощность суглинков лежит в пределах 4.3 м. Из суглинка сложена защитная дамба. Алевролит — сцементированная осадочная горная порода, образуется из дисперсных осадочных пылеватых грунтов (лёссов, лёссовидных грунтов). Аргиллиты — это зацементировавшиеся глинистые частицы, подверженные выветриванию, размоканию в воде, быстрой потере своей структуры, морозному пучению в обнажениях (мощность до 5.8 м).

На поверхности площадки располагаются свозимые на полигон отходы. Они образуют техногенные отложения, включающие насыпные неоднородные, неслежавшиеся и слежавшиеся, уплотненные и рыхлые грунты. По составу грунты, сложенные из бытовых отходов и отходов производственной и хозяйственной деятельности, состоят из полиэтилена (20–95%), строительного мусора (15–30%), текстиля (10–20%), макулатуры (8–20%), пластика (9–15%), древесины (8–20%), стекла (7–15%), металла в виде тросов, проволоки, кусков арматуры (7–15%), минерального грунта ( ∼ 10%), строительного мусора (10–20%) и прочего (6–15%).

• 3.    Математическая модель распространения фильтрата

  • 3.1.    Управляющие уравнения

Численное моделирование распространения фильтрата из пруда-отстойника выполнено при помощи пакета вычислительной гидродинамики ANSYS Fluent с использованием ламинарной модели течения в пористой среде. Задача решалась в рамках нестационарного изотермического подхода. Для перехода от непрерывной расчетной области (Рис. 1) к дискретной сгенерирована пространственная сетка, состоящая из четырехсторонних элементов. Движение фильтрата описывалось моделью Бринкмана, которую авторы ранее использовали в работе [20] .

Уравнения движения в тензорной форме записывались так:

^a^ ⁺ f i >=0-∂t ∂x i

d / 1    \ d /1      \ dp d \ ^ (d vi \ 1 g v+dXj (.m2 pVi Vj)=-dX"+dXj [m'dj) J- K Vi+pgi i где t — время, m и K — пористость и проницаемость пористой среды, ρ — плотность загрязненной жидкости, vi — компоненты вектора скорости (i = 1, 2, 3), g — кинематическая вязкость жидкости, gi — ускорение свободного падения. Зависимость плотности от концентрации примеси c полагалась квадратичной: P = P0 + Ac+Bc2, где p0 = 999.993 кг/м3, A = 667.8, B = -0.1229. Считалось, что тяжелая примесь не создает неустойчивой стратификации по плотности при скоплении фильтрата вблизи дна пруда-отстойника.

Уравнение переноса примеси имело вид:

∂

— (mpc)+ V^ (p v c) = -V J . ∂t

Здесь J — диффузионный поток примеси, определяемый выражением

J = -pDmVc, где Dm — заданный коэффициент молекулярной диффузии.

При проведении вычислений использовался метод конечных объемов. Для выполнения пространственной дискретизации уравнений применялась схема точности 2-го порядка. Временная эволюция моделировалась по явной схеме 2-го порядка аппроксимации. Концентрация примеси бралась в весовых процентах (вес%), и могла варьироваться от 0 до 1 вес%.

• 3.2.    Граничные условия

Задача (1) – (4) решалась при физических характеристиках пород, подстилающих площадку полигона ТКО, представленых в таблице, и разных условиях на границах расчетной области (Рис. 1) :

– на нижней границе (первый водоупор) использовались условия прилипания и нулевого потока массы:

∂c vx = Vy =vz = 0,  —=0;                                 (5)

∂ n

– на входе в каждый слой задавалась скорость в соответствии с характерным для породы коэффициентом фильтрации (см. Табл.). Вектор скорости потока фильтрата имел перпендикулярное входной границе направление V = { V, 0,0 } ); концентрация c принималась равной C ₀ — фоновой концентрации загрязняющего вещества в воде:

V x = V,  V y = 0,  V z = 0,   c = C o ;

– верхней границей служила свободная поверхность жидкости в отстойнике. Она полагалась недеформируемой; на ней считались отсутствующими нормальная компонента скорости, касательные напряжения и поток примеси:

, \ n dVx dVz       dvy dvz

(vn) = 0,  --I— = 0,  --h-— = 0,

∂x  ∂x      ∂x  ∂x∂ zx  zy

– аналогичные условия ставились на боковых поверхностях;

– условия на выходе (индекс out) заключались в выполнении баланса массы со входом (индекс in):

j> pv_mdS -

S in

I pV out dS = 0.

S out

Кинематическая вязкость принималась равной j = 9.34 • 10 ⁷ м ² /с , коэффициент молекулярной диффузии — D = 1.0 Л0 ^-9 м ² /с.

В качестве начальных данных использовались: C ₀ — фоновая концентрация загрязняющего вещества во всем расчетном объеме полигона и v x = V — скорость основного течения, равная скорости на входе в породные слои. Физические характеристики пород, подстилающих площадку полигона ТКО, представлены в таблице.

• 4.    Результаты численного эксперимента

На твердых стенках расчетной области выполнялись условия прилипания и непроницаемости для вещества. Поверхности жидкости в пруде-отстойнике и в озере за дамбой полагались свободными от касательных напряжений.

Численное моделирование распространения фильтрата проводилось для геометрии, показанной на рисунке 1. Водонасыщение техногенного слоя отходов (тела полигона) за счет осадков учитывалось в течение всего расчетного времени. Рассматривалось поведение фильтрата с концентрацией сухого остатка (dry residue)

Таблица. Физические характеристики пород в основании полигона ТКО

Материал	Коэффициент фильтрации, м/сут	Пористость m	Проницаемость K , м 2	Сопротивление горных пород, 1/м 2	Скорость на входе V , м/с	Концентрация c , вес%
Насыпной грунт	0.6	0.4	1.06·10 - 12	9.42·10 11	6.9·10 - 6	0.0047
Суглинок	0.0065	0.702	1.15·10 - 14	8.69·10 13	7.52·10 - 8	0.000342
Алевролит	0.008	0.481	1.42·10 - 14	7.06·10 13	9.26·10 - 8	0.000342
Аргиллит	0.024	0.542	4.25·10 - 14	2.35·10 13	2.78·10 - 7	0.000342

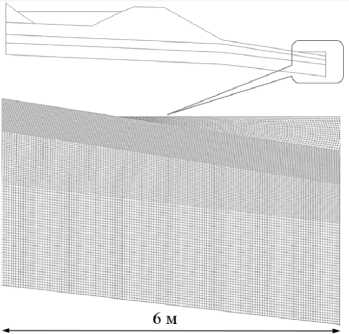
Рис. 2. Фрагмент расчетной сетки, отвечающий озеру за дамбой и окрестности слева от него

C dr = 4700 мг/л. Сухой остаток характеризует общее содержание примесей в воде как растворенных, так и взвешенных, без газов и летучих веществ.

Скорость течения загрязненной воды в слоях породы определялась по характеристикам, взятым из архивных данных полевых измерений 2017 года. Проницаемость и пористость сред представлены в таблице. Уклон поверхности водоупора в районе полигона считался равным 0.02. Начальная концентрация примеси полагалась однородной по всем слоям и равной фоновой концентрации, начальная скорость считалась нулевой. Исследовался процесс распространения фильтрата через суглинистое дно пруда-отстойника на участке заданной площади в ходе длительной эксплуатации полигона. Расчеты проводились для значений физических параметров и концентрации сухого остатка в фильтрате, измеренные также в ходе изыскательных работ 2017 года. На рисунке 2 показана расчетная сетка (в разрезе), состоящая из прямоугольных элементов, сетка содержит 143336 узлов.

Расчеты выполнены в предположении, что, вследствие водонасыщения за счет осадков, тело полигона (техногенный слой) является источником фильтрата, непрерывно поступающего в пруд-отстойник со скоростью V = 6.83 · 10 ^-6 м/с. Эта скорость найдена на основе измеренного коэффициента фильтрации тела полигона. Рассматривался фильтрат, характеризующийся концентрацией сухого остатка C dr = 4700 мг/л, что соответствует значению, задаваемому в расчетах как параметр начального состояния (0.0047 вес%) на входе в породные слои. Фоновая концентрация примеси составляет 250 мг/л или 0.00025 вес%. Временная динамика распространения фильтрата из пруда-отстойника показана на рисунках 3 и 4. Рисунок 3 демонстрирует картины течения фильтрата от полигона до озера за дамбой в зависимости от времени. Рисунок 4 содержит поля концентрации примеси в разные моменты времени после попадания в озеро высоконцентрированного фильтрата.

Основное направление распространения фильтрата наблюдается в горизонтальном направлении, при этом каждая из пород, подстилающих полигон, характеризуется проницаемостью и пористостью, равнозначными по вертикальному и горизонтальному направлениям, то есть в пределах своего слоя среды являются изотропными. Изначально фильтрат просачивается в толщу дамбы (Рис. 3а – г ), затем стекает по естественному уклону основания полигона. За неделю после начала движения фильтратом заполняется край дамбы, обращенный в сторону озера (Рис. 3в ). Через три недели непрерывной фильтрации в полностью увлаженной пористой среде фильтрат попадает в слой алевролита (Рис. 3г ). После этого заполнение фильтратом пространства в вертикальном направлении интенсифицируется. Через 2.5 месяца фильтрат вместе с грунтовыми водами распространяется в слое аргиллита. После смешения с грунтовыми водами загрязненная жидкость проходит в три раза большее расстояние по горизонтали, нежели до момента попадания в слой аргиллита (Рис. 3е ).

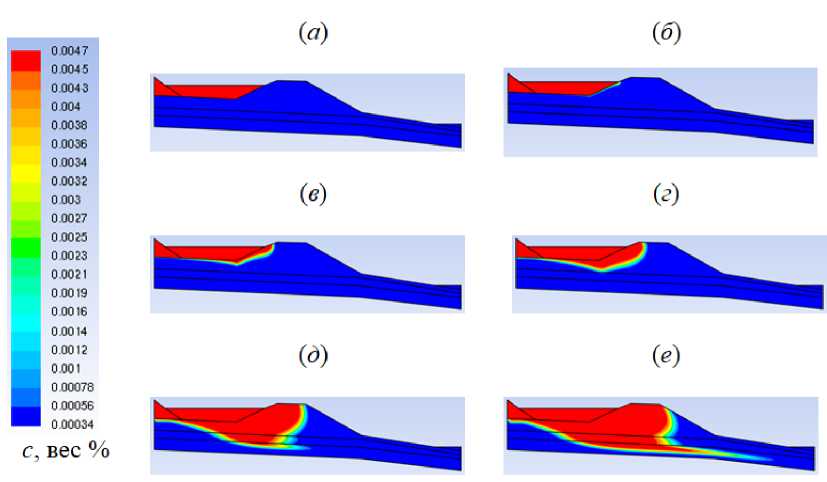
Рис. 3. Картины вычисленного поля концентрации примеси через разные периоды времени после начала истечения фильтрата из пруда-отстойника: через 1 ч ( а ), через 1 сут (24 ч) ( б ), через неделю (7 сут) ( в ), через три недели (21 день) ( г ), через два месяца (61 день) ( д ), через три месяца (92 дня) ( е )

В течение 3 месяцев дамба практически полностью пропитывается фильтратом. При этом в озеро за дамбой фильтрат попадает через его дно (Рис. 4) . На рисунке 4б , г , е показана область вблизи озера за дамбой. Концентрация примеси в озере начинает увеличиваться спустя 4 месяца от момента истечения фильтрата из пруда-отстойника. Просочившийся в водоносный горизонт с грунтовыми водами фильтрат растекается за пределы полигона. Со временем концентрация примеси в озере растет и выходит на насыщение (Рис. 5) .

Расчеты проведены в предположении постоянной максимальной водонасыщенности тела полигона, когда пористая среда полностью заполнена водой с примесью. В природных условиях влажность пород в верхних горизонтах меняется в зависимости от времени года и погоды. Так, весной или после обильных осадков она повышается. Максимальная влажность в течение года в регионе местонахождения полигона наблюдается в общей сложности около одного календарного месяца. С учетом этого фильтрат достигнет максимальной концентрации в озере за дамбой примерно через 4–5 лет при условии максимально измеренного уровня осадков. Данные натурных измерений предыдущих лет подтверждают этот результат. Фильтрующая способность дамбы должна подвергаться регулярному мониторингу. При насыщении дамбы фильтратом необходимо обновление экранирующих сооружений. Поэтому важно знать, за какой период времени происходит насыщение экранных сооружений эксплуатируемого объекта.

• 5.    Заключение

ТКО на полигоне подвержены процессам разложения, в результате которых органические и неорганические растворимые соединения при взаимодействии с атмосферными осадками переходят в раствор. Фильтрат, образующийся в теле полигона при длительной эксплуатации, представляет особую опасность для окружающей среды, так как является токсичным раствором с концентрацией загрязняющих веществ, значительно превышающей предельно допустимые нормы. Фактором отрицательного воздействия фильтрата, образующегося в свалочных наслоениях, на компоненты природной среды и на человека служит его проникание в грунтовые и, в последующем, в поверхностные воды. В средней полосе Российской Федерации каждый гектар, занятый под складирование ТКО, продуцирует ежегодно около 1 тыс. м ³ высоко концентрированного фильтрата. Его утилизация включает отведение, системы сбора и очистки.

На территории рассмотренного полигона загрязненная жидкость по дренажной системе стекает в пруд-отстойник. Расчет выполнен для объекта, эксплуатируемого более тридцати лет. Численно исследован процесс перетекания фильтрата через дно накопителя в слои подстилающих пород. Получены оценки времени установления стационарного профиля концентрации, времени продвижения примеси до ближайшего водоема

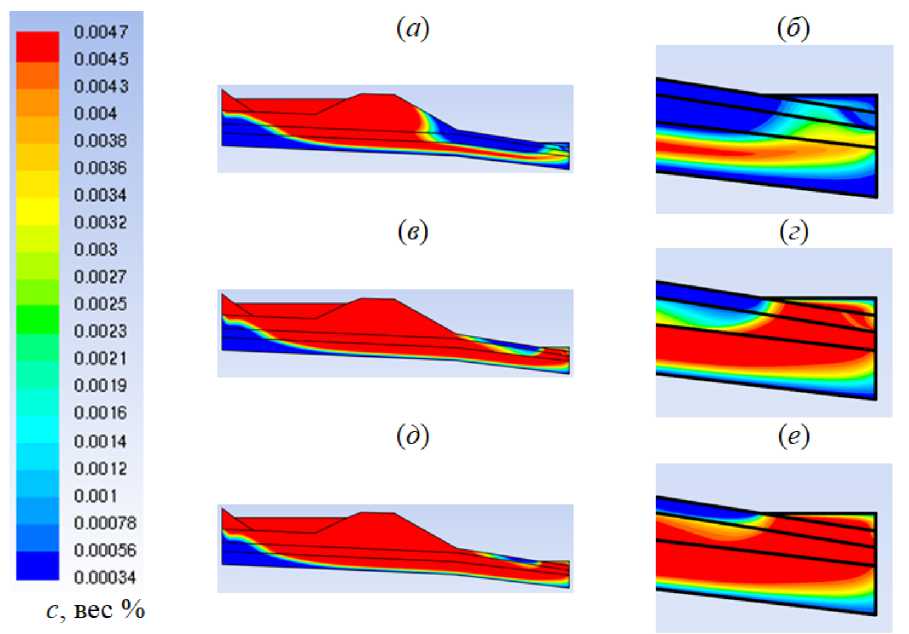
Рис. 4. Общий вид ( а , в , д ) и увеличенные фрагменты ( б , г , е ) картин распределения концентрации фильтрата после достижения им озера за дамбой: через 121 сут ( а , б ), через 180 сут ( в , г ), через 200 сут (6.5 месяца) ( д , е ) от момента начала движения из пруда-отстойника

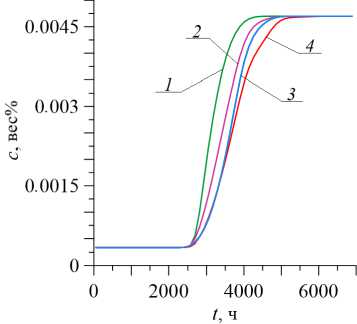
Рис. 5. Временная динамика концентрации в озере за дамбой в точках над уровнем дна, [м]: 0.1 (линия 1 ), 0.5 ( 2 ), 1 ( 3 ), 1.5 ( 4 )

(озера за дамбой, которой обвалована площадка полигона) и значения концентрации в точке поступления в водоем без учета и с учетом слабой адсорбции загрязнений в грунте. С помощью численного моделирования прослежены основные стадии процесса распространения примеси, по результатам вычислений построены картины концентрации в разные моменты времени. Оценена фильтрующая способность дамбы, защищающей природную среду от попадания в нее фильтрата ТКО. Показано, что в предельном случае максимального количества осадков фильтрат достигнет озера за дамбой через 4–5 лет.

Исследование выполнено за счет гранта Российского научного фонда (проект № 23-11-00214)