Численное моделирование накопления повреждений и развития усталостной трещины в упругих материалах

Исследованию процессов накопления повреждений во взаимосвязи с развитием трещин в последние десятилетия уделяется большое внимание [1–4]. Одним из эффективных путей решения задач данного типа является использование численных методов, например метода конечных элементов (МКЭ). Применение МКЭ для описания роста трещины обычно предполагает оперативную перестройку конечно-элементной сетки по мере развития трещины. Это позволяет избежать паразитного влияния топологии конечно-элементной сетки на траекторию развития трещины, так как первоначально построенная сетка по мере продвижения трещины теряет способность

адекватно описывать новое распределение напряжений и деформаций. Однако применимость такого подхода ограничена классом задач, где не рассматривается связь распространения трещины с предысторией накопления повреждений в материале.

При исследовании и моделировании усталостных трещин, распространение которых тесным образом связано с информацией о предыстории повреждений в микроструктуре материала, перестроение сетки без привлечения дополнительных сложных процедур неприемлемо, так как оно приводит к стиранию информации о деградации структуры.

Настоящая работа посвящена формулировке и реализации принципов построения фиксированной сетки конечных элементов, которая позволяет решить эту проблему. Благодаря моделированию всего процесса развития усталостной трещины на одной сетке конечных элементов удается, с одной стороны, естественным образом сохранять информацию об уровне поврежденности, предшествующем разрушению элемента, а с другой стороны, минимизировать влияние сетки на траекторию усталостной трещины. Разработана оригинальная структура КЭ сетки, отвечающая предложенным принципам и проведена ее верификация.

2.    Разработка структуры сетки конечных элементов

Возникновение и развитие очагов разрушения, подрастание усталостных трещин в пластине с отверстием при циклическом нагружении исследуется с помощью конечноэлементной модели, в которой конечные элементы рассматриваются как элементы структуры материала, способные аккумулировать поврежденность. Такой подход позволяет явным образом моделировать развитие очагов разрушения. Для демонстрации особенностей задачи используются регулярные конечно-элементные сетки с различными топологиями. Процесс усталостного разрушения моделируется как накопление повреждений в конечных элементах c использованием правила Палмгрена–Майнера [5]:

d = n- ,                                                                    (1)

TN

где d — поврежденность элемента; n_t = n ( S i ) — количество циклов, «пробег», при размахе (удвоенной амплитуде) интенсивности напряжений S i , N i = N ( S i ) — число циклов до разрушения, долговечность элемента при напряжении S i (эта величина является характеристикой прочности элемента сетки в зависимости от напряжений).

Долговечность N ( S_i ) определяется формулой Баскена [6]:

N ( S ) = C / S m ,                                                                    (2)

в которой С и m — характеристики материала, определяемые из эксперимента.

Выбор формулы Баскена в качестве критериальной обусловлен тем, что, отражая главное — зависимость долговечности от напряжений, она достаточно проста, легко программируема при конечно-элементных расчетах, часто используется для аппроксимации в инженерных расчетах и принята во многих международных стандартах [7–8].

Подстановка (2) в (1) дает поврежденность в каждом конечном элементе:

d = T Пт = (1/ C ) T nS-' . _iN_{i              i}

а

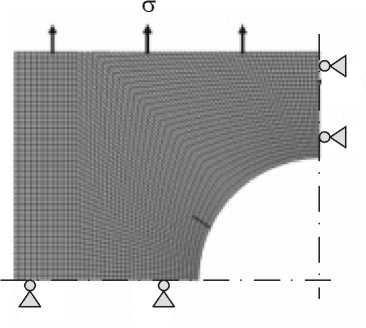
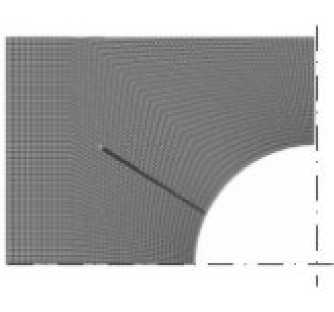
Рис. 1. Расчетная схема пластины с начальной трещиной ( а ) и рост начальной трещины ( б )

б

Разрушение элемента происходит, когда поврежденность становится равной единице, d = 1; оно моделируется уменьшением его жесткости на несколько порядков. Развитие дефекта (трещины) моделируется как последовательное разрушение элементов.

Этот сценарий реализован для решения задачи о росте начальной трещины в тонкой прямоугольной пластине с центральным отверстием под действием циклической нагрузки. Поля напряжений определяются в рамках линейной теории упругости. На предварительном этапе задача решается с применением стандартной регулярной конечно-элементной сетки, состоящей из четырехузловых четырехугольных элементов.

На рисунке 1 показана сетка в начальном состоянии пластины с надрезом, находящемся в стороне от плоскости симметрии, и конечное состояние, соответствующее ускоренному росту трещины в условиях циклического растяжения пластины.

Рисунок свидетельствует, что траектория трещины полностью подчиняется конфигурации сетки, а не следует площадкам главного растягивающего напряжения. Попытки измельчения сетки перед вершиной трещины при сохранении ее регулярного характера не изменяют траектории трещины. Такое поведение трещины, имитируемой последовательным уменьшением жесткости элементов сетки вследствие накопления повреждений, объясняется тем, что максимальные напряжения и, соответственно, интенсивное накопление повреждений реализуются в элементе, располагающемся на продолжении трещины. При регулярном типе сеток такой элемент всего один, и, следовательно, отклонение траектории от прямолинейной, определяемой конфигурацией сетки, не может произойти.

Очевидно, что для минимизации влияния топологии сетки на распространение трещин необходимо добиться рассредоточения локального поля напряжений и повреждений перед вершиной трещины. Сформулируем требования, которые следует предъявить к конечно-элементным сеткам, чтобы осуществить эту идею.

• 2.1.    Обеспечение возможности свободного поворота траектории трещины

согласно локальным полям напряжений и повреждений

Реализация данного требования сводится к необходимости наличия в вершине дефекта области из треугольных элементов, расположенных таким образом, чтобы иметь всего одну общую точку с вершиной дефекта. В этом случае возникает возможность поворота трещины в «истинном» направлении, то есть в соответствии с локальными полями напряжений (и повреждений).

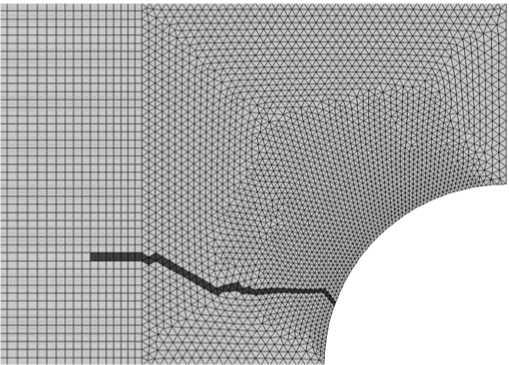
Рис. 2. Рост начальной трещины на треугольной сетке

Отметим, что создания произвольной сетки из треугольных элементов недостаточно для возможности поворота трещины в «истинном» направлении. На рисунке 2 приведена траектория распространения трещины в задаче, аналогичной представленной на рисунке 1, но с использованием сетки из треугольных элементов.

Характер распространения трещины, представленный на рисунке 2, свидетельствует, что простого применения треугольных элементов также недостаточно, так как распространение трещины всё равно происходит только в направлении элемента, находящегося на продолжении трещины, то есть имеющего с вершиной две общие точки. Отличие от прямоугольной сетки состоит лишь в том, что расположение элемента — продолжения трещины относительно направления распространения трещины, может изменяться в силу нерегулярности треугольных сеток, изменяя тем самым и направление распространения трещины. Причем это изменение направления связано исключительно с сеточными явлениями и может происходить вопреки физике процесса. На рисунке 2 это подтверждается изменением горизонтальной траектории распространения трещины, связанным исключительно с изменением топологии сетки.

Поэтому в вершине дефекта необходимо не только наличие треугольных элементов, но и их специальное расположение.

Поскольку заранее предсказать положение вершины трещины затруднительно, возможность ее поворота может обеспечиваться путем создания во всей рассматриваемой области равноотстоящих друг от друга «блоков» из треугольных элементов. Тогда между этими «блоками» траектория может быть и прямолинейной, а в самих «блоках» может происходить определение направления распространения. При достаточно близком взаимном расположении «блоков» получаемая траектория, навязанная конечно-элементной сеткой, не будет существенно отличаться от «истинной» траектории.

• 2.2.    Изотропность сетки

Сетка должна быть изотропной во избежание появления какого-либо выделенного направления, что может привести к сильному влиянию топологии сетки на траекторию распространения трещины. Добиться изотропности сетки можно двумя противоречащими друг другу способами: построением сетки с высокой степенью

Рис. 3. Ячейка предложенной конечно-элементной сетки симметрии расположения элементов или построением сетки с высокой степенью хаотичности расположения элементов. Построение высокосимметричной сетки (в идеале изотропной) полностью контролируется пользователем, так как разбиение осуществляется фактически «вручную» и гарантирует получение требуемой симметрии. Хаотичная же сетка строится автоматически на основании встроенных в вычислительный комплекс алгоритмов. При этом не гарантируется, что в какой-то области разбиения не возникнет сетка с преимущественным направлением, которое окажет сильное влияние на траекторию распространения трещины. Поэтому при решении задачи со случайным распределением прочностных свойств в материале невозможно отделить изменение траектории, вызванное «нехаотичностью» сетки в данной области, от изменения траектории, вызванного неравномерностью распределения прочностных свойств. Данное соображение свидетельствует в пользу увеличения степени симметрии расположения элементов как инструмента для создания изотропных сеток, пригодных для решения данного класса задач.

На основании вышеизложенных принципов проведен поиск вариантов конечноэлементной сетки, отвечающей сформулированным требованиям. В результате данного поиска предложена сетка, ячейка которой представлена на рисунке 3.

Ячейка состоит из «блоков-кругов», в центре которых расположены треугольные элементы, обеспечивающие «свободу» выбора направления подрастания трещины. Идея состоит в том, что в центре «блока-круга» осуществляется выбор направления роста под влиянием поля напряжений и накопленного повреждения в элементах (сопротивление усталости элементов может быть случайной характеристикой, отражающей особенности эволюции дислокационной структуры и ориентации скольжения), а затем подрост трещины происходит до следующего блока. Таким образом, траектория распространения трещины представляет собой ломаную линию, которая при малых размерах ячеек сетки слабо отличается от «истинной» траектории.

Предложенная ячейка обладает совместностью с компонентами регулярных сеток и высокой степенью симметрии, что говорит об изотропности сетки и отсутствии «главного» направления; последнее снижает паразитное влияние топологии сетки на траекторию трещин.

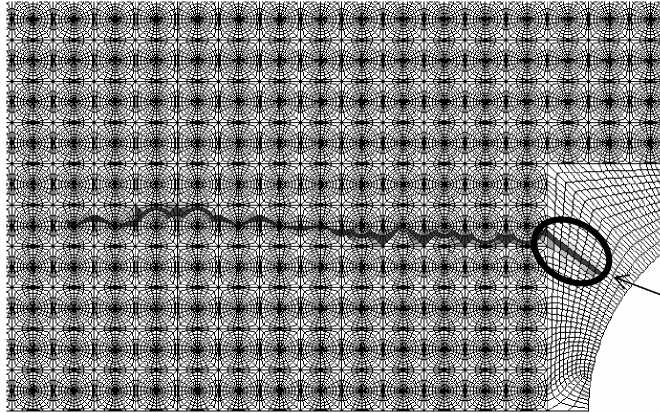
Применение предложенной сетки в задаче о росте начальной трещины (Рис.1, а) при различных направлениях циклического нагружения показано на рисунках 4, 5. Характер распространения усталостной трещины адекватен физике процесса — трещина распространяется перпендикулярно действию приложенной нагрузки. Отметим, что начальная трещина на рисунке 5 оказывается «спящей», а усталостная трещина развивается вследствие накопления повреждений естественным образом из области концентрации напряжений.

На рисунке 6 показана траектория трещины при одновременном двухосном циклическом нагружении с одинаковыми амплитудами по обеим осям. Ломаный характер траектории распространения трещины из начального надреза выявил необходимость дальнейшей модификации рассматриваемой сетки. Несмотря на то, что общее направление распространения трещины отвечает приложенной нагрузке, рост трещины происходит только по границам ячеек. Это делает полученную траекторию излишне ломаной. Поэтому необходимо обеспечить возможность поворота траектории, если трещина проходит по границе предлагаемых ячеек конечно-элементной сетки.

начальная трещина

Рис. 4. Распространение усталостной трещины в случае одноосного нагружения (вертикально ориентированное циклическое нагружение)

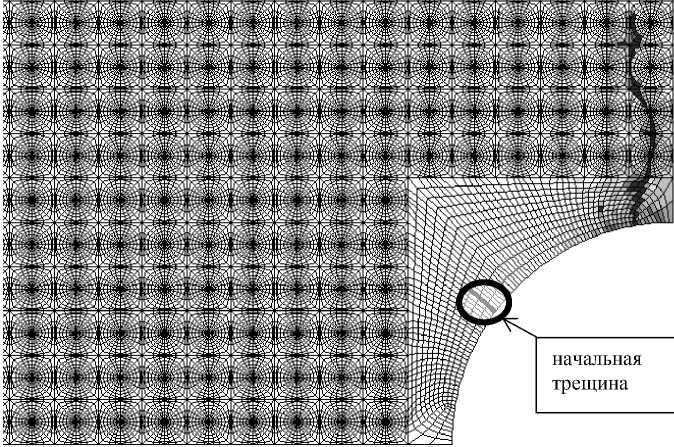
начальная трещина

Рис. 5. Распространение усталостной трещины в случае одноосного нагружения (горизонтально ориентированное циклическое нагружение)

начальная трещина

Рис. 6. Распространение усталостной трещины в случае двухосного циклического синфазного растяжения

Принципы построения ячеистой сетки используются в следующей ее модификации, сочетающей достоинства предыдущего варианта с уменьшением выявленного влияния конфигурации сетки. Фрагмент модифицированной версии сетки представлен на рисунке 7.

Вид данной ячейки свидетельствует, что предлагаемая топология сетки является двухуровневой. Первый уровень состоит из больших «блоков-кругов», в центре которых расположены треугольные элементы, позволяющие поворачивать траектории распространения дефекта. Второй уровень образуют малые «блоки-круги», в центре которых также расположены треугольные элементы. Назначение второго уровня заключается в том, чтобы трещина была способна изменить направление подрастания даже при развитии по границе больших «блоков-кругов».

Следовательно, эта версия ячеистой конечно-элементной сетки должна обеспечить плавность поворота при сохранении «естественного» выбора направления подрастания трещины при нахождении ее вершины в любой точке сетки. Эта конструкция сетки должна значительно снизить влияние топологии на полученную траекторию распространения и уменьшить ее отличие от «истинной» траектории.

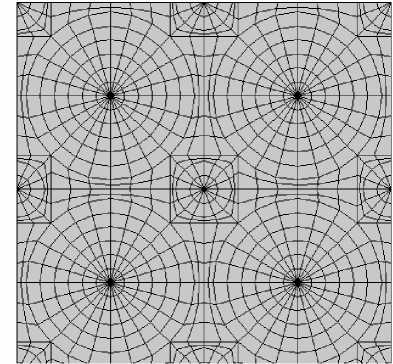
Рис. 7. Ячейка модифицированной конечно-элементной сетки

^SgS. s№^-^-^?®^^.^№£?^

0<<0,2

0,2 <  d <0.4

i^^e 0.4 <<0.6

I^^H 0.6 <<0.8

^^B 0,8 < < 1,0

а                              б

Рис. 8. Начальное распределение дефектов ( а ), траектория распространения дефектов ( б )

Палитра поврежденности элементов:

Рассмотрим конечно-элементное решение задачи о развитии случайным образом распределенных начальных дефектов в материале под действием циклических нагрузок с использованием «двухуровневой» ячеистой сетки. Направление приложенной циклической нагрузки — вертикальное.

Результаты представлены на рисунке 8 и демонстрируют преимущества решения задачи накопления повреждений и развития начальных дефектов в условиях циклического нагружения на зафиксированной сетке. Можно поэтапно проследить образование очагов поврежденности вблизи начальных дефектов, накопление повреждений и развитие дефектов с образованием «макролидера». Имеется возможность оценки размеров очагов поврежденности, а также степени поврежденности материала на каждом этапе нагружения.

Траектория трещины («макролидера») ( d = 1) показывает возможность поворота траектории, если этого требуют локальное напряженно-деформированное состояние и «история» накопления повреждений. В данном случае причинами отклонения траектории трещины от прямолинейной, очевидно, являются влияние накопленных повреждений в поле, где происходит подрост трещины, а также развитие дефекта в нижней части пластины. Пример показывает, что модификация ячейки позволяет добиться существенного снижения влияния топологии сетки на траекторию трещины. Следует также отметить «плавность» изменения траектории как результат использования модифицированной сетки, представленной на рисунке 6.

3.    Верификация предложенной сетки

Точность предложенной двухуровневой ячеистой сетки проверяется на значениях коэффициентов интенсивности напряжений (КИН). Для этого значения КИН, вычисленные МКЭ на основе предложенной сетки, сравниваются со значениями, найденными также МКЭ, но с использованием сингулярных элементов, и со значениями, взятыми из справочной литературы.

В качестве верификационной рассматривается задача об одноосном растяжении пластины конечных размеров с центральной сквозной трещиной. На рисунке 9 представлена расчетная схема задачи. В силу симметрии рассматривается четверть пластины с соответствующими условиями на границах. Трещина показана в правом нижнем углу.

Значения геометрических параметров: длина трещины — 2 l = 4 мм, размеры пластины — 2 а = 2 b = 28 мм. Приложенное внешнее растягивающее напряжение — σ = 1 MПa, размеры ячейки первого уровня в предложенной сетке — 2×2 мм.

Согласно справочнику [9], значение КИН K_I ^Мур для данной задачи имеет вид:

1/2

К ^Мур = G^l • F I ( a ), a = l/b , F I ( a ) = 1 sec yl .

В случае использования предложенной сетки значение КИН определяется в результате экстраполяции к вершине трещины [10]:

К, етка = lim о 41П ,

I        r ^ 0

где r — расстояние от вершины трещины; о = о ( r ) — значение напряжений в элементах на продолжении трещины.

В случае использования сингулярных элементов значение КИН K_I ^синг вычисляется с помощью встроенной в программный комплекс процедуры, основанной на методе узловых перемещений.

Для рассматриваемой задачи имеют место следующие значения КИН:

• -    из справочника [9] — КМур = 80,3 кПа^м¹/²;

• -    КЭ-модель с сингулярными элементами — К™^нг = 81,6 кПа^м¹/²;

• -    КЭ-модель на основе предложенной сетки — к^с,етка = 78,5 кПа^м¹/².

4.    Заключение

Относительная разница результатов составляет 2,5%, что свидетельствует о приемлемой точности результатов, полученных с помощью предложенной версии сетки.

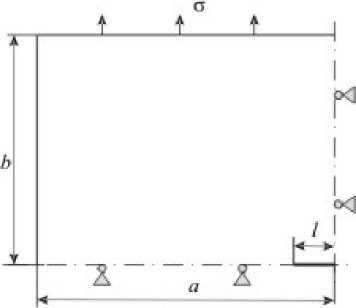
Рис. 9 . Схема пластины с трещиной

Разработана двухуровневая конечно-элементная сетка на основе сформулированных принципов построения сетки конечных элементов для решения задачи исследования взаимосвязи процессов накопления повреждений и развития усталостной трещины.

Проведена верификация предложенной сетки с целью оценки чувствительности траектории трещины к топологии сетки и точности расчета КИН при ее использовании. Показано, что отклонение величины коэффициента интенсивности напряжнений от справочных данных составляет менее 3%.

Продемонстрировано, что двухуровневая ячеистая сетка обеспечивает моделирование подрастания трещины в соответствии с локальным полем напряжений и полем повреждений в элементах (структуры материала). Влияние топологии сетки может быть приемлемым при дальнейшем развитии модели усталости поликристаллической структуры.

В результате получен эффективный инструмент для конечно-элементного моделирования накопления повреждений и развития усталостной трещины в материале. Моделирование учитывает связь кинетики распространения усталостных трещин в упругом материале с информацией о текущем накоплении поврежденности в рассматриваемой области в процессе циклического нагружения.

Работа выполнена при поддержке Программ фундаментальных исследований Отделения энергетики, машиностроения, механики и процессов управления РАН «Трибологические и прочностные свойства структурированных материалов и поверхностных слоев», проекта, финансируемого Sandia National Laboratories (США, Livermore), Российского фонда фундаментальных исследований (проект № 07-01-00525) и Правительства Санкт-Петербурга.