Численное моделирование нелинейных процессов накопления повреждений при циклических нагружениях

Анализ результатов экспериментальных исследований малоцикловой усталости [1, 2] показывает, что процесс накопления повреждений является существенно нелинейным и его нелинейность возрастает с уменьшением амплитуды деформации (напряжения). Мерой нелинейности процесса накопления повреждений является степенная зависимость числа циклов N от повреждения ω ( N = N_f ω ⁿ , n ≥ 0, где N_f — число циклов до разрушения).

При нестационарных (нерегулярных, многоблочных) режимах циклического нагружения история нагружения оказывает существенное влияние на усталостную долговечность. Экспериментальными исследованиями [3] при двухблочном нагружении установлено, что при переходе с большей амплитуды на меньшую происходит уменьшение суммарной долговечности по сравнению с долговечностью, полученной согласно правилу линейного суммирования повреждений, а при переходе с меньшей на большую — увеличение суммарной долговечности. Таким образом, наблюдается нарушение правила линейного суммирования повреждений.

Совместное математическое моделирование упругопластических процессов и нелинейных процессов накопления повреждений при произвольных режимах циклического нагружения как пропорциональных (простых), так и непропорциональных (сложных) возможно только на основе эволюционных уравнений деформирования и накопления повреждений, так как напряженно-деформированное состояние и повреждение в этом случае являются функционалами процесса нагружения. Примерами таких уравнений служат эволюционные уравнения, построенные на основе современных моделей термопластичности [4, 5]. Данные модели относятся к классу теорий течения при комбинированном упрочнении, а в качестве энергии, отвечающей за процесс накопления повреждений в них, принимается энергия, равная работе

микронапряжений на поле пластических деформаций. Ответственность микронапряжений (остаточных микронапряжений) за процесс накопления повреждений впервые отмечена в работе [6], экспериментальное обоснование этого утверждения содержится в работе [7], а кинетическое уравнение, описывающее работу микронапряжений на поле пластических деформаций (критерий работы микронапряжений), впервые рассмотрено в работах [8, 9] при теоретическом исследовании малоцикловой усталости конической оболочки при теплосменах; здесь также критерий работы микронапряжений впервые апробирован при непропорциональном (сложном) неизотермическом нагружении.

2.    Математическое моделирование процессов деформирования и накопления повреждений

Для описания процессов деформирования и накопления повреждений обратимся к двум направлениям теории пластичности: теории упругопластических процессов на основе общей математической теории пластичности А.А. Ильюшина [10, 11] и теории течения при комбинированном упрочнении на основе концепции микронапряжений В.В. Новожилова [12]. В теории первого направления деформации не делятся на упругую и пластическую, а в теориях второго направления такое разделение присутствует. В работах [13, 14] на основе уравнений второго направления [5] получены аппроксимации функционалов пластичности теории упругопластических процессов, относящейся к первому направлению. Главной особенностью варианта теории упругопластических процессов из [13, 14] является использование, во-первых, дополнительных уравнений для внутренних переменных и, во-вторых, двух состояний — упругого и пластического, но без разделения деформации на упругую и пластическую.

В варианте теории упругопластических процессов [13, 14] вводится понятие поверхности нагружения — поверхности, которая выпукла со стороны упругой области и может смещаться и изотропно расширяться (сужаться): |S - A| - C B ( 5 ) = 0. Здесь S — вектор напряжений [10, 11]; A — вектор смещения центра поверхности нагружения (вектор микронапряжений); C B ( 5 ) — скаляр, отвечающий за размер (радиус) поверхности нагружения; s — длина дуги траектории деформаций. Поверхность нагружения вводится для того, чтобы разделить упругое и пластическое состояния.

Упругое состояние имеет место, когда изображающая точка напряженного состояния находится внутри поверхности нагружения или вектор приращения деформаций d Э направлен внутрь поверхности нагружения, то есть

|S - A| <  C B ( 5 ) U ( S - A ) • d Э <  0. (1)

В этом случае уравнения, моделирующие деформирование и накопление повреждений в рамках рассматриваемого варианта теории упругопластических процессов, будут выглядеть следующим образом:

dS

--= 2 G , dsds dA = 0, ds d?. 0.

ds

Среда пребывает в пластическом состоянии, когда изображающая точка напряженного состояния находится на поверхности нагружения и вектор приращения деформаций направлен в сторону выпуклости поверхности нагружения, то есть

IS - a| = CB (5) n (S - A)• dЭ > 0,(5)

и уравнения варианта теории упругопластических процессов запишутся как

— = Nd! + N э + N s ,

ds   ds dA

~r = gB -r+ g3 Э + g A A, dsds

d to

a- 1

— = ato

ds

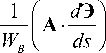
^a О A I |^A - ^EA ^Э| ) n " .

К уравнениям (1)–(9) следует добавить уравнение, связывающее шаровые составляющие тензоров напряжений ( с ) и деформаций ( б ):

g = 3 K б .

Для функционалов пластичности N , N_Э и N_A имеют место следующие аппроксимации [13, 14]:

N = g B - g A C B ^{( 5 )+ d}C B ^{( 5} ) ,     ^NЭ = g э ,     N A = g A ,                      ⁽¹¹⁾

ds gB = Ea +P a G a ,    дэ =в a Ea ,    gA =-в a .                          (12)

В уравнениях (5)-(12) приняты обозначения: E A , в A , с A , W B — параметры анизотропного упрочнения и энергия разрушения (материальные параметры среды, определяемые на основе базового эксперимента); K , G — упругие параметры; C B ( 5 ) — функция изотропного упрочнения; a и n _a — функция и параметр нелинейности процесса накопления повреждений (при n _a = 0 процесс накопления повреждений является линейным).

Уравнение (6) аналогично уравнению, принадлежащему А.А. Ильюшину [10, 11, 15] и полученному им для случая обобщенной плоской задачи. Здесь же уравнение следует из общих соотношений теории пластического течения [13, 14] при комбинированном упрочнении [5] без введения каких-либо ограничений на вид задачи, что делает возможным его применение не только для плоской задачи. Следует отметить, что исходные соотношения теории пластического течения при комбинированном упрочнении [5, 16, 17] применимы для произвольных процессов сложного нагружения как по плоским, так и пространственным траекториям, что обосновывается сравнением результатов расчетных и экспериментальных исследований на широком спектре конструкционных сталей и сплавов и программ сложных нагружений [16, 17]. Уравнение (6), будучи достаточно простым вариантом теории упругопластических процессов, весьма перспективно для адекватного описания произвольных плоских и пространственных процессов сложного нагружения.

Полученная система уравнений (1)–(12) представляет собой задачу Коши с тривиальными начальными условиями, для численного решения которой используется метод Рунге-Кутты четвертого порядка точности.

3.    Базовый эксперимент

Расчетно-экспериментальный метод определения (идентификации) материальных функций по данным базового эксперимента изложен в работах [5, 13, 14]. Согласно этому методу для определения материальных функций достаточен минимальный набор данных базового эксперимента, включающий: – упругие параметры, которые определяются традиционными методами;

– диаграмму растяжения до деформации 0,05–0,1, построенную в координатах S ₁, Э ₁ векторов напряжений и деформаций;

– данные циклического нагружения при постоянном размахе деформации 0,02–0,03: число циклов до разрушения (появление макротрещины длиной 1 мм) и стабилизированную циклическую диаграмму (петлю пластического гистерезиса) также в координатах S ₁ , Э ₁ ;

– число циклов до разрушения при двухблочном циклическом нагружении в условиях как увеличения, так и уменьшения размаха деформации.

Для нержавеющей стали 304 на основе экспериментальных данных [18] получены следующие материальные функции: G = 769000 МПа; C B = 120 МПа; E A = 3500 МПА; в A = 200; с A = 140 МПа; W B = 2600 Дж/см³; n _a = 1,5, а для стали AISI 304 функции находились по данным работы [19]; при этом значения материальных функций оказались такими же, как для стали 304, исключение составила энергия разрушения — W B = 3700 Дж/см³.

4.    Нелинейные процессы накопления повреждений

Для осуществления численного интегрирования уравнений (1)–(12) (решения задачи Коши) необходимо перейти от параметра нагружения s (длины дуги траектории нагружения) к параметру нагружения t (времени) и разрешить все уравнения относительно первой производной по t . Тогда при задании траектории деформаций (случай жесткого нагружения) будут определены вектор деформации и его производные по времени, то есть становятся известными правые части дифференциальных уравнений. Численное интегрирование полученной системы уравнений производится на основе метода Рунге-Кутты четвертого порядка точности.

Расчетные исследования малоцикловой усталости нержавеющей стали 304 проведены при пропорциональном симметричном жестком циклическом нагружении как при постоянной амплитуде

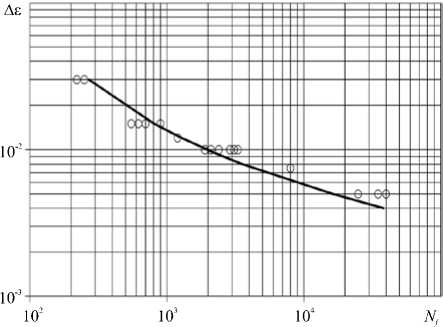
Рис. 1. Кривая малоцикловой усталости стали 304

деформации, так и при ее блочном изменении. На рисунке 1 сплошной линией показана расчетная кривая малоцикловой усталости, а светлыми кружками — экспериментальные данные [18].

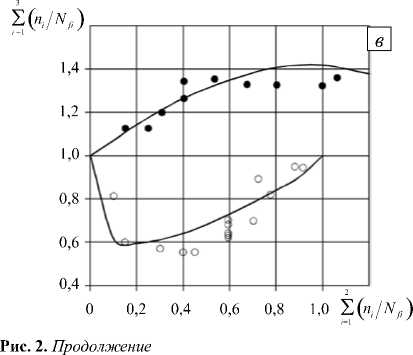
Нелинейный процесс накопления приведен на рисунке 2. Результаты расчетов накопления повреждений при различных амплитудах деформации одноблочного циклического нагружения (Рис. 2, а) свидетельствуют, что с уменьшением амплитуды деформации нелинейность процесса возрастает, а с увеличением амплитуды деформации нелинейность ослабевает и процесс накопления повреждений стремится к линейному виду.

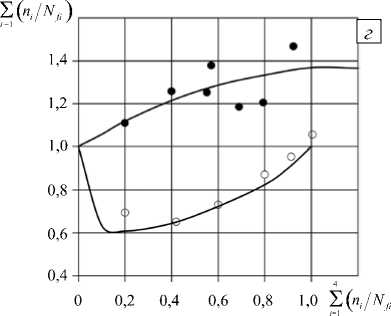
Нарушение правила линейного суммирования повреждений при многоблочном изменении амплитуды деформации следует из результатов, приведенных на рисунках 2, б, в, г, соответственно, при двухблочном, трехблочном и пятиблочном изменении амплитуды деформации. Здесь Nfi — число циклов до разрушения при размахе деформации i -го блока; ni — число

m циклов нагружения на i -м блоке; ni Nfi — повреждение на i -м блоке; ∑ni Nfi — повреждение на m i=1

блоках (разрушение при ω=1 ). Результаты расчетов изображены сплошными линиями, а результаты экспериментов [18] кружками, темными при возрастании размаха деформации (0, 005 → 0, 015 , Рис. 2, б; 0,005→0,01→0,015, Рис. 2, в;   0,005→0,008→0,01→0,012→0,015, Рис. 2, г) и светлыми при убывании размаха деформации ( 0, 015 → 0, 005 , Рис. 2, б; 0, 015 →0,01 →0, 005 , Рис. 2, в; 0, 015 →0, 012 →0,01 →0, 008 →0, 005 , Рис. 2, г). При многоблочном изменении амплитуды наблюдается существенное отклонение от правила линейного суммирования повреждений при удовлетворительном соответствии результатов расчетов и экспериментов.

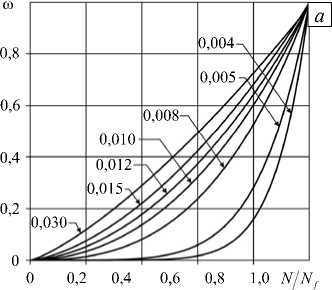
Рис. 2. Накопление повреждений при различных амплитудах деформации одноблочного циклического нагружения ( а ); суммирование повреждений при двухблочном ( б ); трехблочном ( в ); пятиблочном ( г ) изменении амплитуды деформации

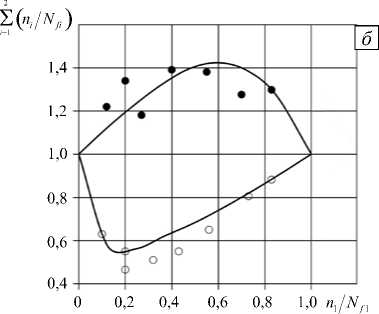
Расчетные исследования малоцикловой усталости нержавеющей стали AISI 304 проведены

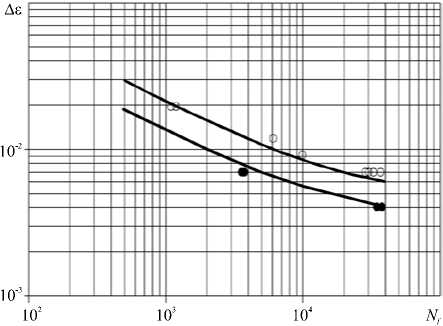
Рис. 3. Кривые малоцикловой усталости нержавеющей стали AISI 304

как при пропорциональном жестком циклическом нагружении, так и при непропорциональном (сложном) циклическом нагружении по траектории деформаций в виде окружности. Результаты расчетов изображены на рисунке 3 сплошными линиями, а результаты экспериментов [19] кружками — светлыми при пропорциональном нагружении и темными при непропорциональном (сложном) нагружении.

Наблюдается значительно больший повреждающий эффект от действия непропорционального нагружения по сравнению с пропорциональным — снижение долговечности происходит практически на порядок. Соответствие результатов расчетов и экспериментов удовлетворительное.

5.    Заключение

Численное моделирование нелинейных процессов накопления повреждений на основе рассмотренного прикладного варианта теории упругопластических процессов и кинетического уравнения накопления повреждений адекватно описывает произвольные процессы деформирования и накопления повреждений как при стационарных, так и нестационарных, а также пропорциональных и непропорциональных режимах циклических нагружений. Анализ полученных результатов говорит о повышении долговечности практически на 40% при возрастании размаха деформаций и снижении долговечности практически на 40% при убывании размаха деформаций в условиях многоблочных циклических режимов нагружения. Возрастание сложности процесса циклического нагружения приводит к снижению долговечности практически на порядок. Сравнение результатов расчетов и экспериментов говорит об их надежном соответствии.