Численное моделирование обтекания газовым потоком колеблющейся лопатки

Современная тенденция к росту загруженности рабочих лопаток компрессора турбореактивного двигателя приводит к повышению вероятности возникновения флаттера, который характеризуется резким увеличением амплитуд колебаний лопаток. В результате этого динамические напряжения в лопатках возрастают до недопустимо больших значений и в конечном итоге в течение нескольких минут приводят к усталостным поломкам как самих лопаток, так и лопаточных венцов, в которых они крепятся. Следовательно, проведение исследований с целью прогнозирования возможности возникновения такого опасного эффекта как флаттер является актуальным.

Традиционный подход к расчету флаттера лопаточных венцов основан на частотном анализе [1, 2], в котором колебания лопатки представляются гармонической функцией времени, учитывающей постоянный угол сдвига фаз колебаний соседних лопаток. Но частотный анализ игнорирует влияние потока газа на колебания лопаток. Такое воздействие учитывают методы интегрирования связанной задачи аэроупругости [3, 4 ].

Предлагаемый в данной работе подход также принимает во внимание обратную связь и основывается на гипотезе, согласно которой существенной является только первая собственная форма колебаний с соответствующей собственной частотой. Благодаря этому становится возможным разделить решение задачи на твердотельную

(определение собственных частот и форм) и газодинамическую составляющие. Обоснованность данной гипотезы подтверждается большим количеством соответствующих экспериментальных данных [5]. Гипотеза успешно используется в многочисленных работах для исследования аэроупругого поведения лопаточных венцов в трехмерном потоке идеального [6] и вязкого [7] газа. Основным достоинством предлагаемого подхода, по сравнению с решением сопряженной задачи, является относительная простота, а недостатком — возможность моделировать только установившиеся колебательные процессы.

2.    Постановка задачи

Производится двумерный расчет течения воздуха, набегающего под углом в = 66° со скоростью U на решетку рабочих лопаток, имеющих профиль первой стандартной конфигурации (Рис. 1) [2]. Лопатки совершают крутильные синфазные колебания (угол сдвига фаз колебаний соседних лопаток равен нулю) относительно середины своих хорд с частотой v = 15 Гц и амплитудой колебаний A = 2 ° . Поток воздуха моделируется как течение вязкого сжимаемого газа, используется к - £ модель турбулентности.

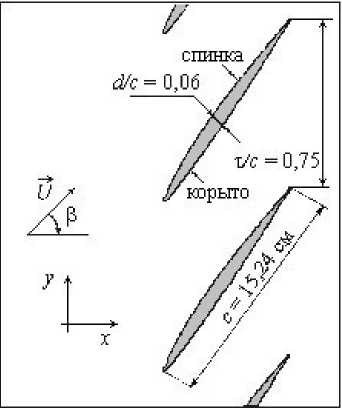
Рис. 1. Решетка рабочих лопаток с профилем первой стандартной конфигурации

На входе в расчетную область задаются полное давление (150000 Па) и температура (300 К) газа, на выходе — давление, среднее по площади выходного сечения (148350 Па). Поверхности лопаток считаются гладкими, адиабатичными и непроницаемыми. Значения параметров на границах расчетной области соответствуют значениям тестового случая 9, рассматриваемого в работе [2].

3.    Построение расчетной модели

Численное моделирование поставленной задачи проводится с помощью программного комплекса ANSYS CFX 11, реализующего метод контрольных объемов с использованием неявной схемы расчетов. Комплекс хорошо зарекомендовал себя в турбомашиностроении при решении многих задач газовой динамики как стационарного, так и нестационарного характера. Геометрия области решения создаётся системой Unigraphics NX 1.0 по координатам точек, взятым в [2].

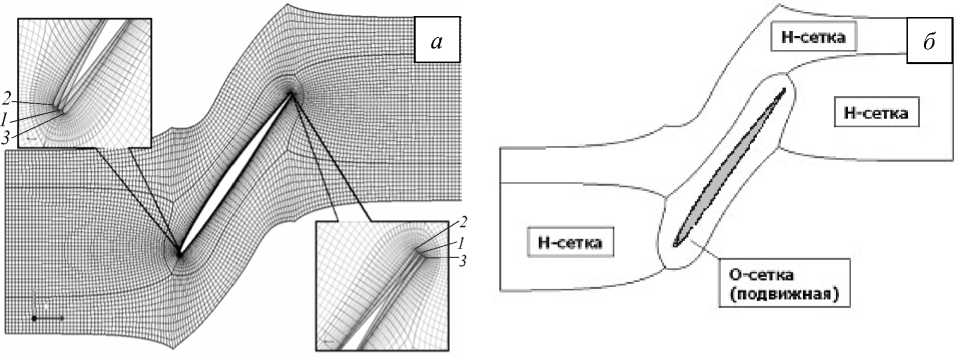
Рис. 2. Общий вид ( a ) и топология ( б ) расчетной сетки

При численном моделировании обтекания газом лопатки, совершающей колебания, одна из главных проблем заключается в необходимости построения подвижной расчетной сетки, согласующейся с границами области. При этом применение стандартной автоматической процедуры перестроения сетки, имеющейся в пакете ANSYS CFX, как правило, приводит к существенному снижению её качества, что отражается на точности получаемых результатов. Преодолеть эту особенность программного пакета можно следующим образом.

Так как амплитуда и частота колебаний лопатки являются заданными (см. постановку задачи), предлагается генерировать подвижную сетку до начала расчета на каждом шаге по времени, разделив процесс на два этапа: сначала строить сетку для нейтрального положения лопатки (Рис. 2, а , положение 1 ), затем определять отклонения координат узлов сетки в рассматриваемый момент времени от их значений в нейтральном положении. На рисунке 2, а также приведены расчетные сетки, отвечающие двум крайним положениям лопатки ( 2 и 3 ).

Структурированная расчетная сетка вокруг лопатки строится таким образом, что можно выделить 4 блока: из них три неподвижных («Н»-сетка) и один подвижный («О»-сетка) (Рис. 2, б ). Узлы «О»-сетки движутся по гармоническому закону:

N _m Г , X                                        , X                               -i

* ( n )                                          * ( n )

= x^ + X xsi, j • sin (n • 2nv-1) + xci, j • cos (n • 2nv-1) ,

s si

x i , j

n =1 ^L

где i , j — индексы узлов сетки; n — номер гармоники; N _а = 4 — число гармоник; xs /J , xc /J — коэффициенты, вычисляемые из решения линеаризованных уравнений Уинслоу (Winslow) [8].

Расчетная сетка строится с помощью программы MeshTools 1.1b, разработанной в Инженерном центре ОАО «НПО «Сатурн». Её размерность составляет 15400 узлов; вдоль межлопаточного канала располагается 150 ячеек, поперек — 40, по границе профиля лопатки — 160; толщина пристеночного слоя ячеек составляет 50 мкм.

Временной интервал, соответствующий одному периоду колебаний T = v ^{- 1} , разбивается на N = 100 промежутков (их число выбрано исходя из результатов предварительных расчетов). Таким образом, шаг по времени составляет A t = 6,540 ^{- 4} c. Для каждого момента времени t = k •A t ( к = 0,..., N ) записывается файл с координатами узлов расчетной сетки.

4.    Стационарный расчет

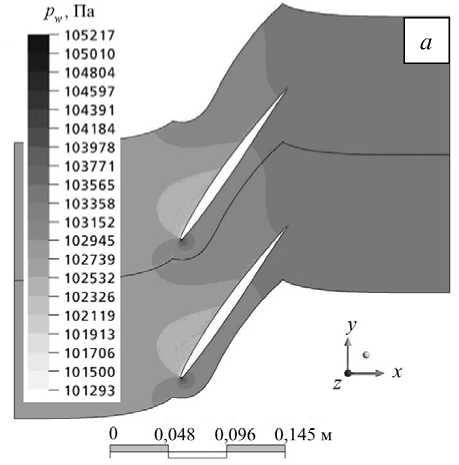
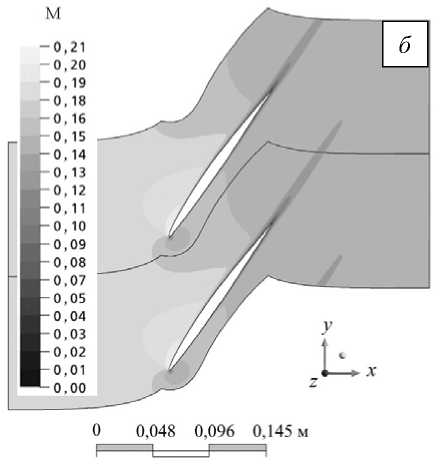
Построенная расчётная модель используется далее для получения стационарного решения задачи обтекания набегающим потоком вязкого газа неподвижной решетки лопаток. В качестве критерия сходимости принимается условие достижения максимальными невязками параметров течения значений ниже 10^-5. Распределение статического давления p_w и числа Маха M представлено на рисунке 3.

Р„Па [ 105217 105010 104804 104597 104391 104184 103978 103771 103565 И- 103358 ■ - 103152 1 - 102945 1- 102739 102532 102326 - 102119 101913 - 101706 - 101500 - 101293

0.048 0,096 0,145 м

а

-0,21 -0,20

-0,19 -0,18

-0.16 - 0,15 г 0.14

-0,12 -0.11 -0,10 0,09 1-0,08 1-0.07 1-0,05 1-0.04 1-0.03 1-0.02 1—0,01 *-0.00

0,048 0,096 0.145 м

б

Рис. 3. Распределение статического давления ( a ) и числа Маха ( б )

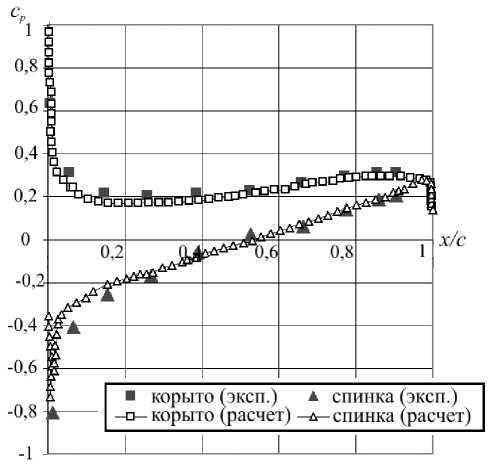
Рис. 4. Распределение коэффициента давления по профилю лопатки

По вычисленным значениям давления находится распределение по поверхности лопатки коэффициента давления:

c p

pw

=

^- Р 1

-

p ₁

где p_w — статическое давление в соответствующей точке поверхности лопатки;

p ₁ — среднее по площади входного сечения значение статического давления; P ₁ ^* — полное давление на входе. График распределения коэффициента давления по профилю лопатки, представленный на рисунке 4, свидетельствует о хорошем совпадении результатов расчета стационарной задачи с данными натурного эксперимента [2].

5.    Нестационарный расчет

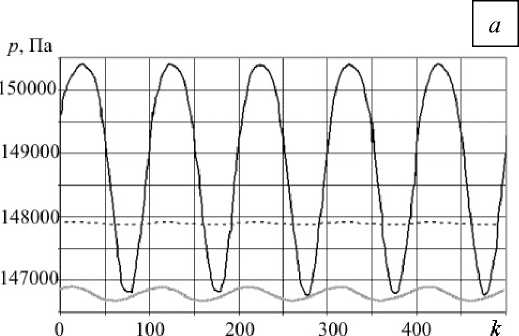
Нестационарный расчет проводится до момента установления периодического режима течения газа. Сходимость решения контролируется путем наблюдения за значениями параметров в характерных точках расчетной области: на входной кромке (точка mp1), в зоне следа за лопаткой (mp2) и в межлопаточном канале (mp3). График изменения давления в контрольных точках и расположение этих точек в расчетной области содержит рисунок 5.

|---mpl -••-mp2  ---mp3 |

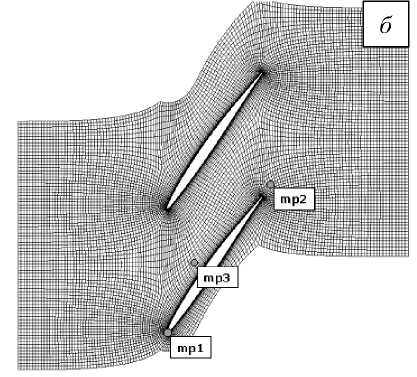
Рис. 5. Графики изменения давления в контрольных точках ( а ) и расположение контрольных точек в расчетной области ( б )

Величина невязки вычисляется по формуле:

5 ( k) =(p( k)- p^k k - N )V k>N, _mp_mp_m ,         ,

где p_m ^{( k )} — давление в контрольной точке m на k -й итерации; N — количество итераций на один временной период. Для полной сходимости потребовалось около 2-х периодов колебания профиля лопатки (Рис. 6).

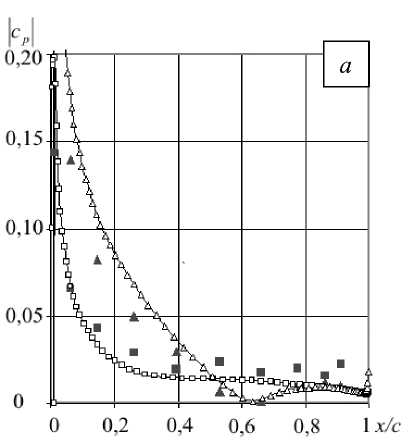
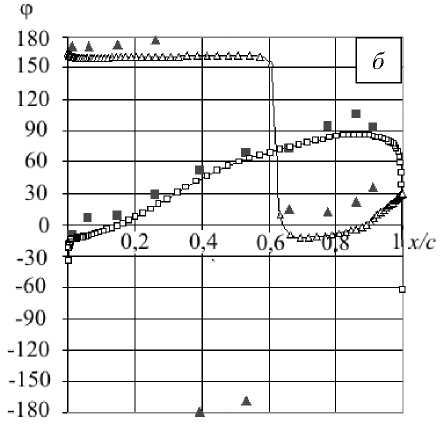
Изменение во времени значений коэффициента давления в точках поверхности лопатки аппроксимируется функцией

Acpj (t) = cpj(t) - cpj = |AcP |j •sin (2nvt + %■), где j — индекс узла на поверхности лопатки; cpj (t), cpj — текущее и среднее значения коэффициента давления в узле j; |Acp| , фj — соответственно модуль и фаза функции A cpj (t).

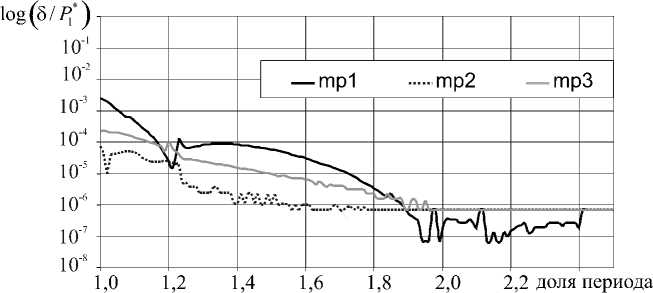
Рис. 6. График сходимости к периодическому решению

■ корыто (эксп.) а спинка (эксп.) -п—корыто (расчет) -^а— спинка (расчет)

Рис. 7. Распределение модуля ( а ) и фазы ( б ) коэффициента давления по поверхности лопатки

Сравнение результатов нестационарного расчета и данных эксперимента приведено на рисунке 7. Характер распределения расчетных значений модуля и фазы коэффициента давления по поверхности лопатки качественно совпадает с экспериментальным; количественно абсолютные значения соответствующих величин имеют незначительные отличия.

По результатам нестационарного расчета определяется работа в межлопаточном канале за один период колебаний:

газа

T

D = Jj ( F S - y S ) dSdt = 7,51 - 10 ’ 5 Дж ,

0S где FS — газовые силы, действующие на лопатку; vS — скорость движения поверхности лопатки; S — площадь поверхности лопатки. Положительное значение параметра D свидетельствует о «склонности» рассматриваемой лопатки к увеличению амплитуды колебаний за счет аэродинамических сил при заданном режиме работы. Однако окончательный вывод о вероятности возникновения флаттера можно получить, только имея данные об инерционных свойствах лопатки и коэффициенте конструкционного демпфирования .

6.    Оценка влияния параметров численного решения

С целью верификации полученных результатов проводится дополнительный, априори более точный, расчет, который выполняется при следующих параметрах численной реализации:

• 1)    расстояния от кромок лопатки до входного и выходного сечений увеличены вдвое;

• 2)    густота сетки увеличена в 2 раза в каждом направлении (Рис. 8);

• 3)    шаг по времени уменьшен в 2 раза;

  

  Рис. 8. Подробная сетка с увеличенными расстояниями до входного и выходного сечений

  
  
  
  
  
  
  
  
7.    Заключение

■ корыто —□— корыто I + корыто '

'эксперимент) * спинка исходный расчет) ^л— спинка ■ уточненный расчет) —о- спинка

'эксперимент) исходный расчет) 'уточненный расчет)

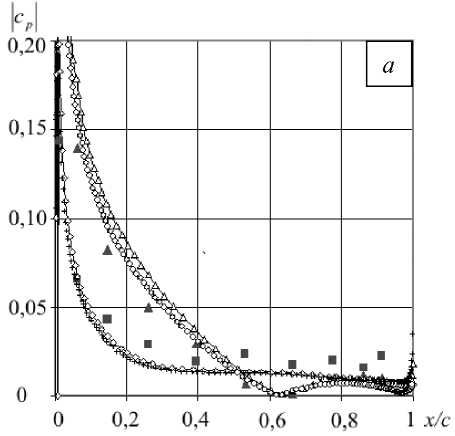
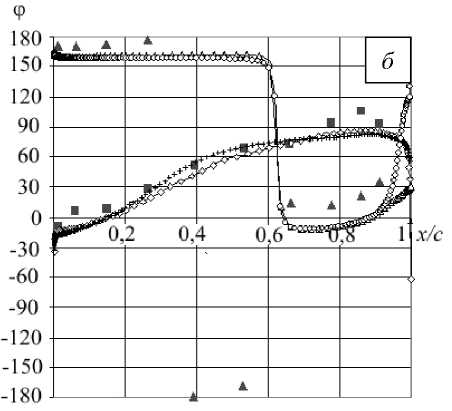
Рис. 9. Распределение модуля ( а ) и фазы ( б ) коэффициента давления поверхности лопатки

Полученные решения свидетельствуют, что уточненный расчет дает несущественное отклонение графиков модуля и фазы коэффициента давления в сравнении с описанным в предыдущем разделе нестационарным расчетом (называемым далее исходным) (Рис. 9). Следовательно, результаты исходного расчета устойчивы по отношению к выбору параметров численного решения.

Результаты решения задачи обтекания двумерной решетки профилей лопаток компрессора потоком вязкого газа, полученные по предлагаемой методике, удовлетворительно согласуются с данными эксперимента.

Предложенный подход может быть обобщён на случай трехмерной геометрии решетки и использован для оценки склонности лопаток компрессора газотурбинного двигателя к флаттеру.