Численное моделирование плоскопараллельного движения конических ударников в грунтовой среде на основе модели локального взаимодействия

и нарушение условий приложения модели при наличии затупления. Ранее [19] изучались силовые характеристики взаимодействия конических ударников с грунтом при ударе и наклонном проникании без учета трения. Было показано, что квадратичная по скорости МЛВ, удовлетворительно описывающая процесс внедрения конического ударника по нормали к поверхности грунта, с несколько большей погрешностью может употребляться и при наклонном внедрении. В данной работе для конических ударников с различным углом раствора и углом падения проводится сравнение сил сопротивления, траекторий движения центров масс и углов поворота, полученных в рамках квадратичной МЛВ, с аналогичными результатами компьютерного моделирования в полной трехмерной постановке при учете трения.

Для описания плоскопараллельного движения твердого конического тела, имеющего высоту h и радиус основания R , рассмотрим его сечение плоскостью, проходящей через оси неподвижной системы координат O rz , ось O z которой совпадает с осью симметрии тела, а ось O r перпендикулярна ей и проходит через центр основания конуса. Для плоской фигуры уравнения движения и вращения вокруг центра масс C (Рис. 1), согласно [28], имеют вид:

M w C = F ,     J C m = K ,

где M — масса тела; w _C и F — вектор ускорения центра масс и главный вектор сил, действующих на тело; ю — вектор угловой скорости вращения относительно оси, перпендикулярной плоскости движения и проходящей через центр масс; J _C и K — момент инерции и момент сил относительно этой же оси; точкой обозначено дифференцирование по времени. Введем также подвижную систему координат O'r'z' , связанную с телом и в начальный момент времени совпадающую с системой координат O rz.

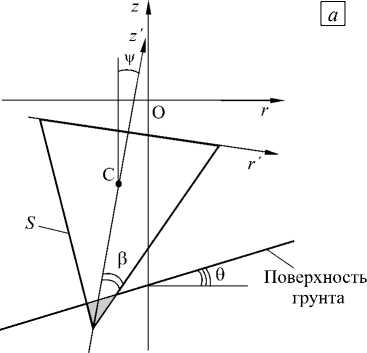
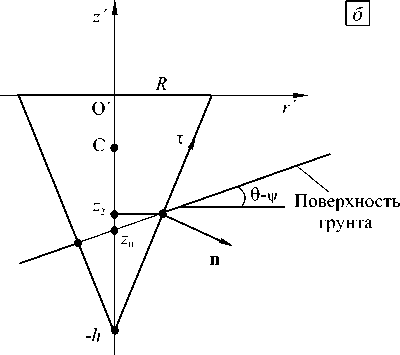
Рис. 1. Схемы к постановке задачи исследования движения конуса в грунтовой среде

Проектируя векторные равенства (1) на оси системы координат O ' r'z ' и учитывая соотношения w C = y C + ю х у C ( у C — вектор скорости центра масс [28]), получим:

M ( v _r ‘ -to v z ‘ ) = F_r, ,    M ( v_z , +ю v r ‘ ) = F_z, ,    J C to = J C V = K ,

где v r , , v_z , и F_r ' , F_z , — проекции векторов у C и F на координатные оси O r ' , O z ' ; ю — проекция вектора угловой скорости ю на ось, перпендикулярную плоскости движения ( ю _r, = ю _z, = 0), v — угол поворота вокруг центра масс.

В дополнение к подвижной системе координат O ' r ' z' введем локальную координатную систему, связанную с боковой поверхностью S проникающего тела и образуемую вектором внешней нормали n и касательным вектором τ (Рис. 1 б ) Компоненты главного вектора сил F и величину момента сил K в соотношениях (2) найдем, прибегнув к интегрированию контактных напряжений, возникающих на поверхности S :

z 2 ^ф ₂                                                                  z 2 ^ф ₂

F r - = J J r ( z ')( с n +о _т tg P ) cos ф d ф dz ' ,    F z - = J J r ( z ' )( -o n tg P + o_T ) d ф dz ' ,

• - h 0                                                            - h 0

z 2 ф ₂

K = J J r ( z ' ) [ ( r '- r C )( ^- G n tg P + G_I ) ^- ( ^z '- ^z C )( O n +G_T tg P ) ] cos ф d ф dz ' ,

- h 0

где r ( z ') — радиус окружности сечения конуса плоскостью z' = const; ф — угол, образующийся между радиусом r ( z ') и положительным направлением оси r' в поперечном сечении конического ударника с углом раствора 2 р ; g n и g_t — нормальные и касательные напряжения в элементе тела, определяемом углом ф и координатой z' ; r' , z' и r C , z C — координаты точки приложения вектора сил и центра масс соответственно.

Величины ф ₂, r ( z ') и z ₂ в (3), аналогично [29], рассчитываются по формулам

(               r                  z '- z o ₊ (а \          ^z о + h tg P tg ( ^0- v )

r =( h+z> tge, ф = “ 7( 0 полагаем ф2 = 2п, z2 = 0.

В соответствии с МЛВ считаем, что каждый элемент поверхности тела взаимодействует со средой независимо от других участков тела. Также принимаем, что нормальное напряжение представляется в виде квадратичной зависимости от скорости, а касательное напряжение является кусочно-постоянной функцией и описывается законом Кулона

^G n /р0 = ^- H ( v n ) ( A^ n + Bv n + C ) , ^G T =- sgn v т k f |^G n | ,                         ⁽⁴⁾

где H — функция Хевисайда; A , B и C — постоянные коэффициенты, зависящие от физикомеханических свойств среды, формы ударника и других составляющих; р ₀ — начальная плотность среды; v n и v _т — нормальная и касательная компоненты вектора скорости внедрения, имеющей место в сечении конуса плоскостью ф = const, проходящей через ось симметрии; k f — коэффициент трения. Если v n <  0, то g n = 0 , что соответствует отрыву среды от тела.

Величины сил в (3) при отсутствии отрыва потока и условии k_f = 0 обозначим верхним индексом 0, тогда, с учетом (4), получим следующие оценки:

F « ( 1 - k f tg p ) F r 0,      F « ( 1 + k f ctg p ) F_z °.                             (5)

Компоненты вектора скорости в локальной системе координат вычислим по формулам vn = (vr' -(z‘ -zC)to)cosфcosP-(vz +(r‘ -rC )tocosф)sinP ,   gT = Y + kp ;

v _T = ( v_r . - ( z' - z C ) to ) cos ф sin P + ( v z + ( r' - r C ) to cos ф ) cos P .

Для завершения описания движения необходимо конкретизировать способ задания параметров модели среды и МЛВ (4). Положим, что грунтовая среда упругопластическая, с линейными функциональными зависимостями gt = Y + kp ,   p = Kee,   c = a + X U,                              (6)

при этом g _t — ее предел текучести, p — давление, e — объемная деформация, c — скорость ударной волны, U — массовая скорость за фронтом ударной волны, K_e — модуль объемного сжатия, постоянные Y и k отвечают за сцепление и внутреннее трение грунта, величина a характеризует скорость распространения волны сжатия в грунте при малых давлениях, X — предельную сжимаемость грунта.

Параметры МЛВ, в соответствии с известным подходом [30], найдем из приближенного решения задачи расширения сферической полости [24, 31–33]. Для модели среды (6) это решение записывается следующим образом:

G = p c ² 5 ,     Р = Р ₀ /( 1 -S 3 ) ,     е = U/c ,    c = X ^1/3 U + a /3,

( Ц- 2)(2 ц- 1)

^{2 ц + 1} _с1-2ц ,\.

—У- ¹ ■ в ^{4 - 2 ц}1в ² - ( 1 +в^{- 2 ц} ) Y , Ц- 2 J ^v 'ц

ц = к/ ( 1 + 2/3 к ) , ц* 0, ц* 0,5,

где ст — напряжение на границе полости, U — скорость расширения полости, р — плотность грунта за фронтом ударной волны.

Аналитическое решение (7), полученное в предположении несжимаемости среды за фронтом ударной волны, учитывает динамическую сжимаемость и сопротивление грунта сдвигу в рамках модели (6). Чтобы сделать решение применимым в расчетах, в формуле (7) положим ст n = ст , v n = U . Коэффициенты A , B и C в заданном диапазоне изменения скоростей определим методом наименьших квадратов. Таким образом, движение тела во времени представляется решением задачи Коши для системы обыкновенных дифференциальных уравнений (2) относительно величин v r , , v z , , ю и V при следующих начальных условиях ( t = 0 ):

V r - = 0,     V z - =- V ),    ю = 0, V =0.                                  (8)

Задача Коши (2), (8) решалась численно, методом Эйлера, на отрезке времени [ 0, T ] с постоянным шагом A t . На каждом временном отрезке кратный интеграл (3) вычислялся путем последовательного интегрирования по переменным ф и z , после чего осуществлялось суммирование результатов по всем отрезкам, и получалась составная формула Симпсона.

В момент полного погружения тела в грунт подынтегральные выражения в (3), описывающие силу сопротивления и момент сил в подвижной системе координат O ' r ' z ' , являются полиномами степени не выше третьей относительно переменных ф и z . В силу этого формулы интегрирования четвертого порядка позволяют точно установить величины силовых характеристик в каждый момент времени при отсутствии отрыва потока среды от поверхности тела.

Тестирование численной методики решения системы уравнений (2)–(8) осуществлялось с использованием полученных ранее (см. [19]) аналитических выражений для компонент вектора силы и момента (без учета трения), которые применимы только с момента полного погружения тела до начала отрыва среды от тела. Расчеты проводились при следующих значениях параметров: a = 516,4 м/с; Х = 0,5; р ₀ = 2000 кг/м³; Y = 0,5 МПа; к = 1,0; V ₀ = 150м/с; k_f = 0,3 . Значения коэффициентов трехчленной МЛВ (4) при изменении скорости v n в диапазоне от 30 м/с до 100 м/с составили: A = 1,2; B = 0,95 V ; C = 0,034 V 00 [19].

Для верификации изложенной методики на основе МЛВ также рассматривалась задача проникания конического ударника в упругопластическую среду с учетом кулоновского трения. Задача имела полную трехмерную постановку и решалась с помощью коммерческого программного продукта LS-DYNA. Ударник моделировался как недеформируемое жесткое тело (*MAT_RIGID), грунт — как упругопластическая среда (*MAT_SOIL_AND_FOAM), поведение которой, согласно модели, описывалось как (см. [34]) ст T = 3 ( a ₀ + a 1 p + a ₂ p ² ) , p = K e e . Для приведения в соответствие этих выражений связи предела текучести с давлением и давления с объемной деформацией с принятыми линейными зависимостями (6) полагали, что a ₀ = Y ²/3 , а 1 = 2 kY /3, a ₂ = к ²/3 , K_e = р ₀ a ²/(1 + 2 к /3 ) .

Решение проводилось в постановке FSI (Fluid Structure Interaction), при которой уравнения движения ударника интегрировались в лагранжевой системе координат, а при получении уравнений для грунта использовалась эйлерова сетка. Взаимодействие ударника и упруго-пластической среды изображалось специальным типом контакта (CONSTRAINED_LAGRANGE_IN_SOLID).

В качестве тестовых примеров рассмотрено проникание под углом 9 = п/3 к свободной поверхности грунта конусов массой M = 40 г с углами полураствора в = л/6, п/4 и п/3 и начальной скоростью V 0 = 150 м/с. Конусы имели постоянный радиус основания R = 0,01 м, а их высота составляла h = Rig в . Координаты центра масс в подвижной системе координат O ' r’z’ равнялись r c = 0 , z_c = - h /4 , момент инерции — J_c = 3 M ( 4 R ² + h ² ) /80.

Погрешность решения задач в пакете LS-DYNA определялась из анализа решений на сгущающихся сетках, фрагмент такой (средней по величине) расчетной сетки приведен в [19]. Силы сопротивления, полученные в численных расчетах, имели осциллирующий в пределах 5-10% характер. Осредненные кривые решений для конкретного конуса, найденные на различных сетках, отличались друг от друга менее, чем на 5%, что было принято за оценку погрешности численных расчетов. Ранее в [19] получено, что погрешность МЛВ (4), (6), (7) при решении задач нормального проникания конуса с углом полураствора в = л/6 не превышает именно 5%. Таким образом, если далее будут возникать бóльшие отличия при описании наклонного проникания, то они не будут связаны с ошибками учета в МЛВ свойств среды проникания.

В процессе счета анализировалось влияние трения на компоненты интегральной силы взаимодействия ударника с грунтом. Компоненты главного вектора силы сопротивления в неподвижной системе координат O rz представлены на рисунке 2 в безразмерном виде. Угол полураствора ударника в и другие характеристики составляли: в = л/4, F* =p ₀V 0² n R 2/ 2, t* = V , h ** , h* = R/tg в + R tg 9 , где время t* соответствует моменту полного погружения тела в грунт (угловое движение в расчет не принималось).

На рисунке 2 кривые 1 , 2 согласуются с осевыми ( F_z ), а кривые 3 , 4 с радиальными ( F_r ) компонентами главного вектора силы сопротивления внедрению. Силы сопротивления внедрению, обозначенные сплошными линиями с номерами 1 , 3 , получены при учете трения Кулона ( k f = 0,3), штриховые линии с номерами 2 , 4 отвечают k f = 0. Наблюдается хорошее качественное совпадение результатов трехмерных расчетов (Рис. 2 а ) и расчетов в рамках МЛВ (Рис. 2 б ), изменение силы сопротивления при учете трения адекватно оценкам (5). Ошибка МЛВ в величине амплитуды сил может превышать 25%, а с учетом трения она становится еще больше.

На рисунке 3 представлены компоненты главного вектора силы сопротивления внедрению конусов с углами полураствора л/6 ( а ) и п/3 ( б) при ударе под углом п/3 к поверхности грунта при учете трения. Сплошными линиями обозначены результаты, полученные в трехмерных расчетах, штриховыми — согласно МЛВ. Кривые 1 , 2 соответствуют осевым компонентам вектора силы, кривые 3 , 4 — радиальным. Видно, что с ростом угла раствора конуса ошибка МЛВ возрастает.

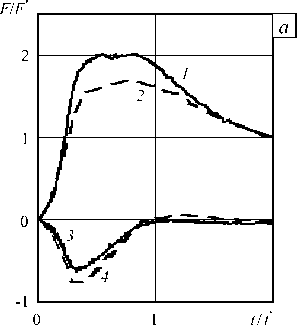
Рис. 2. Безразмерные осевые (кривые 1 , 2 ) и радиальные ( 3 , 4 ) компоненты главного вектора силы сопротивления внедрению, полученные в трехмерных расчетах ( а ) и по МЛВ ( б ) с учетом сил трения ( k f = 0,3 - сплошные линии) и без учета ( k f = 0 - штриховые линии) в задаче внедрения под углом п/3 к поверхности грунта конуса с углом полураствора п/ 4

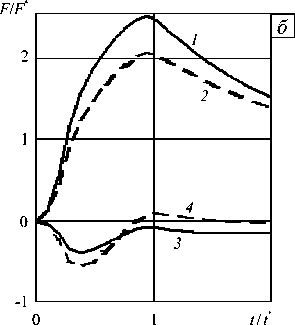
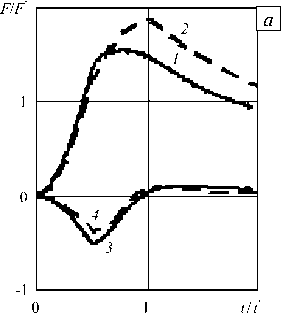
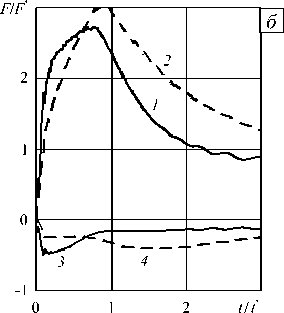
Рис. 3. Безразмерные осевые (кривые 1 , 2 ) и радиальные (кривые 3 , 4 ) компоненты главного вектора силы сопротивления внедрению конусов с углами полураствора п/ 6 ( а ) и п/3 ( б ) при ударе под углом п/3 к поверхности грунта при учете трения; сплошные и штриховые линии – соответственно результаты расчетов в трехмерной постановке и в рамках МЛВ

Как отмечалось ранее [23, 26, 27], с ростом угла раствора конуса ошибка применимости МЛВ к расчету силы сопротивления внедрению по нормали растет, что отмечается и при наклонном проникании (см. Рис 3 и также Рис. 2). Можно предположить, что радиальная компонента вектора силы будет удовлетворительно описываться и для конусов с углом раствора, меньшим п/6.

На рисунке 4 приводятся величины углов поворота вокруг центров масс конусов, имеющих углы полураствора Р = л/ 6, п) 4 и п/ 3 соответственно, в зависимости от безразмерного времени (величина t*

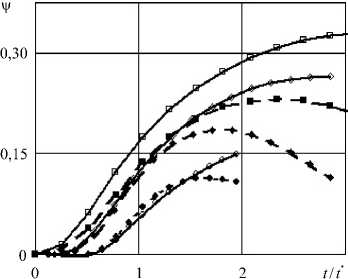
Рис. 4. Угол поворота конуса относительно центра масс в зависимости от безразмерного времени: точки, ромбы и квадраты соответствуют углам полураствора конусов р = п/ 6, п/ 4 и п/ 3; результаты расчетов в трехмерной постановке показаны светлыми маркерами о , о , □ ; по МЛВ -темными маркерами •, ♦ , ■

рассчитывалась отдельно для каждого угла полураствора конуса). Светлыми маркерами обозначены результаты, полученные в численных расчетах в трехмерной постановке, темными — полученные в рамках МЛВ. Отмечается нормализация положения конусов при погружении на глубину, бóльшую высоты конуса (положительное значение угла соответствует повороту против часовой стрелки), а также при этом конус с меньшей высотой имеет бóльший угол поворота. Сравнение результатов расчетов с учетом и без учета трения показало, что кулоновское трения приводит к некоторому увеличению максимального угла поворота, обратно пропорциональному углу раствора конуса. МЛВ качественно описывает эту тенденцию. Удовлетворительное количественное соответствие числовых данных, полученных по различным методикам, наблюдается только на ранней стадии внедрения, увеличение ошибки при использовании МЛВ происходит как с ростом р, так и с ростом глубины погружения.

На рисунке 5 а представлены безразмерные смещения центров масс конусов с углами полураствора Р = п/ 6, п/ 4 и п/ 3 в системе координат O rz . Видно, что преобладает движение в осевом направлении при малом относительном смещении в радиальном направлении.

На рисунке 5 б приведены безразмерные радиальные компоненты векторов скоростей центров масс (отнесены к величине начальной скорости в осевом направлении) в зависимости от безразмерного времени. Компоненты векторов скоростей в осевом направлении не приводятся, так как наблюдается достаточно хорошее совпадение кривых — падение скорости V_z от начальной величины V 0 при t/t* = 1 составляет 18-20%, а при t/t* = 2 находится в интервале 35-45% для всех рассматриваемых конических ударников (величина t/t* = 1 соответствует моменту контакта всей боковой поверхности конусов с грунтом).

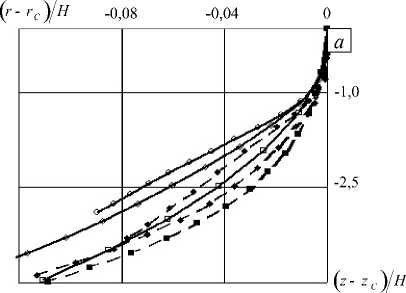
Рис. 5. Траектории движения центров масс конусов ( а ) и радиальные компоненты векторов скорости центров масс в зависимости от времени ( б ); точки, ромбы и квадраты соответствуют углам полураствора конусов р = п/6 , п/4 и п/3 ; результаты расчетов в трехмерной постановке показаны светлыми маркерами о , о , □ ; по МЛВ - темными маркерами •, ♦ , ■

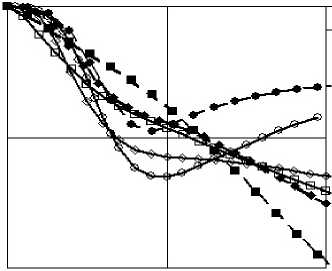
о                             1                         tit*

Таким образом, из полученных результатов следует, что квадратичная по скорости МЛВ, удовлетворительно описывающая движение по инерции конического ударника по нормали к поверхности грунта [19, 23, 26, 27], применима и для описания наклонного внедрения в интервале от tt ^* = 0 до момента контакта всей боковой поверхности конуса с грунтом ( ф* ~ 1). По сравнению с нормальным ударом наблюдается несколько бóльшая погрешность определения силовых и кинематических характеристик, что обусловлено ошибками вычисления нормального напряжения при заданном законе трения Кулона. Учет кулоновского трения приводит к увеличению максимального угла поворота ударника по сравнению с расчетами без трения, и МЛВ качественно описывает эту тенденцию.

Работа выполнена при финансовой поддержке Совета по грантам Президента РФ для ведущих научных школ (НШ-2843.2012.8) и РФФИ (проекты № 13-08-00531_а, 13-08-00658_а).