Численное моделирование процесса агрегации эритроцитов в эксперименте с микропипетками

Взаимодействие эритроцитов при агрегации происходит в среде, содержащей полимерные макромолекулы (декстран, белки плазмы крови – фибриноген и др.). Согласно исследованиям степень агрегации эритроцитов усиливается при различных патологиях (сахарном диабете, гипертензии, малярии и др.) [1, 2].

Предложены две модели, описывающие парную агрегацию эритроцитов в среде, содержащей полимерные макромолекулы: «мостиковая» и «обедненного слоя». Экспериментальные данные показывают, что происходит неспецифическая адсорбция белковых макромолекул на поверхности эритроцитов [3]. Мостиковая модель объясняет взаимодействие эритроцитов при их сближении образованием молекулярных мостиков. При этом силы взаимодействия эритроцитов уравновешивают электростатические силы отталкивания между слоями гликокаликса, покрывающего мембраны эритроцитов [4, 5].

Модель обедненного слоя предполагает, что при контакте поверхности эритроцита с раствором полимера потеря конфигурационной энтропии полимера не уравновешивается энергией адсорбции, и вблизи поверхности эритроцитов возникает обедненный слой, в пределах которого концентрация полимера ниже, чем в объемной фазе. Понижение концентрации полимера в обедненной зоне приводит к перемещению растворителя в объемную фазу и возникновению разности осмотического давления, вызывающего притяжение эритроцитов [5]. Агрегация частиц за счет осмотического давления в обедненном слое в коллоидных системах хорошо изучена и подтверждается

Калягина Надежда Вячеславовна, к.ф.-м.н., доцент кафедры прикладной механики, Москва экспериментально [6–9]. В ряде работ показано, что происходит агрегация фосфолипидных пузырьков [10, 11]. Теорию обедненного слоя подтверждает также тот факт, что агрегация эритроцитов зависит от гидродинамического радиуса Rh макромолекул окружающей среды [12]. Показано, что небольшие белки с гидродинамическим радиусом Rh ≤ 4 нм не индуцируют агрегацию. Многочисленные эксперименты показали, что полимеры среды с равными значениями гидродинамических радиусов, но с различными электрохимическими свойствами показывают сходное влияние на степень агрегации эритроцитов. Агрегация усиливается при увеличении гидродинамического радиуса полимеров среды свыше 4 нм, несмотря на снижение молярной концентрации макромолекул [12].

Изучена зависимость степени агрегации эритроцитов от концентрации полимерных молекул, таких как декстран: агрегация увеличивается с повышением концентрации декстрана и, достигнув максимума, степень агрегации снижается [13, 14]. Такая нелинейная зависимость не может быть объяснена мостиковой моделью. Объяснение механизма агрегации эритроцитов можно найти в работах, посвященных изучению осмотических эффектов в коллоидных растворах, содержащих полимерные молекулы [8, 15]. В этих работах показано, что агрегация коллоидных частиц может уменьшиться в том случае, если молекулярная масса и концентрация полимерных молекул достаточно велики. Эритроциты рассматриваются, как коллоидные частицы. Исходя из этого, на основе экспериментальных данных построена параболическая зависимость степени агрегации эритроцитов от молекулярной массы декстрана, которая достигает максимума при значении массы декстрана, равном 500 кДа [13]. Сила взаимодействия двух жестких коллоидных частиц d (рис. 1, [8]) вызывает некомпенсированное осмотическое давление Р полимерных молекул d , отсутствующих в узкой щели между коллоидными частицами. Сила притяжения коллоидных частиц равна произведению осмотического давления полимерных молекул на площадь их контакта. В случае эритроцитов полимерные молекулы адсорбируются на поверхности слоя гликокаликса эритроцитов, поэтому осмотическое давление Р ′ полимерных молекул в промежутке δ между контактирующими эритроцитами не равно нулю. В этом случае сила притяжения эритроцитов равна произведению разности значений осмотических давлений ( Р – Р ′ ) полимерных молекул на площадь контакта S эритроцитов. При небольших концентрациях раствора среды монотонное увеличение агрегации эритроцитов с ростом концентрации раствора макромолекул вызвано увеличением разницы осмотических давлений между обедненной зоной и объемной

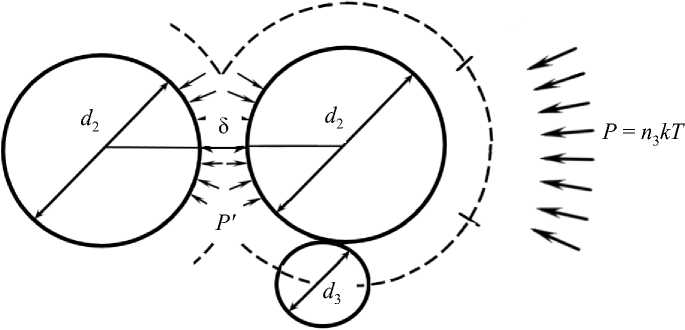
Рис. 1. Схема взаимодействия двух коллоидных частиц с диаметром d в среде полимерных молекул с диаметром d [8]

фазой. С дальнейшим увеличением концентрации макромолекул среды осмотическое давление полимерных молекул в обедненном слое Р ′ растет и выравнивается с осмотическим давлением объемной фазы полимерных молекул Р , что приводит к уменьшению разности осмотических давлений ( Р – Р ′ ) и в итоге – к снижению агрегации.

Эффект ингибирования процессов агрегации усиливается низкомолекулярными декстранами, которые эффективнее адсорбируются на поверхности гликокаликса [14]. Таким образом, модель обедненного взаимодействия является более предпочтительной для описания неспецифической агрегации эритроцитов по сравнению с мостиковой моделью.

Исследования показали, что повышенная вязкость крови, дисфункция эндотелия кровеносных сосудов и повышение давления у больных гипертонической болезнью обусловлены повышенной концентрацией фибриногена [16–18].

Согласно модели обедненного слоя при агрегации в зоне контактного взаимодействия возникают два типа напряжений: нормальные и касательные. Значения этих напряжений для таких многофункциональных объектов, как эритроциты, расчетно-теоретическим способом получить сложно, поэтому их значения целесообразно вычислять, используя эксперименты.

Cтатья посвящена разработке конечно-элементной механической модели нелинейного деформирования тонкостенных оболочек эритроцитов при образовании парного агрегата эритроцитов. Исследовано напряженное состояние зоны контакта, и определены значения контактных напряжений, возникающих при агрегации. Оценка нормальных напряжений притяжения двух эритроцитов выполнена путем сопоставления результатов расчета с результатами эксперимента, в котором агрегация эритроцитов изучалась методом микропипеточной аспирации [19]. Для оценки касательных сдвиговых напряжений использовано приближение Куэтта. Полученные расчетные значения напряжений сопоставлены со значениями, измеренными микрофлюидными методами. Параметры конечно-элементной механической модели эквивалентной оболочки эритроцита определены из двух экспериментов: растяжение эритроцита лазерным пинцетом и аспирация эритроцита гидравлической микропипеткой. Численное исследование напряженного состояния при агрегации эритроцитов позволит количественно оценить факторы, контролирующие процесс агрегации эритроцитов, а также получить значения нормальных и касательных напряжений, возникающих при агрегации эритроцитов в экспериментах, проводимых микрофлюидными методами. В этих экспериментах возможны разные конфигурации взаимодействующих эритроцитов, что влияет на величину сил агрегации или дезагрегации.

Метод расчета процесса агрегации эритроцитов

Расчет процесса агрегации эритроцитов выполнен методом конечных элементов (МКЭ). Механические характеристики оболочки эритроцита, необходимые для расчета, определяют два типа деформации: деформацию при постоянной площади поверхности, обусловленную жесткостью при сдвиге – μ , и изотропное растяжение, зависящее от жесткости при растяжении – K . Благодаря малой величине μ ( μ = 0,007 мН/м [19]) оболочка эритроцита легко меняет форму, при этом возможны большие деформации и перемещения, и зависимость между натяжениями и деформациями носит нелинейный характер [20]. Жесткость при растяжении превышает жесткость при сдвиге на несколько порядков величины, поэтому деформации растяжения малы.

Оболочка эритроцита состоит из двух слоев: липидного бислоя и примыкающего к нему слоя спектрина. Слой спектрина, представляющий собой сеть белковых молекул, имеет нелинейную зависимость деформации от величины натяжения. При малых нагрузках натяжение спектриновой сети незначительно, и жесткость при растяжении всей оболочки определяется жесткостью липидной мембраны (K = 140 мН/м)[21]. В режиме малых натяжений возможно проявление изгибных эффектов. При этом изгибная жесткость оболочки эритроцита равна изгибной жесткости липидной мембраны D = 0,19'10-12 мкН'м. Перечисленные механические характеристики учтены при расчете. В данной работе аппроксимация тонкостенной оболочки эритроцита выполнена осесимметричными конечными элементами с возможностью больших деформаций и перемещений.

Согласно работе [20], функция удельной упругой энергии деформации (упругий потенциал) имеет вид

F = рв + -Ка2, где а - параметр изменения площади, а = Х,Х2 -1; в - параметр изменения формы, в =

2λλ

( ^Х2 + ^Х2 )

- 1; Х и л. - главные кратности удлинений; р = 0,007 мН/м [19]. В

случае малых натяжений оболочки эритроцита площадь поверхности эритроцита не изменяется а = 0, а значения внутреннего осмотического давления q_n<  20 ^ 60 Па (см.

рис. 1). Значения упругого потенциала F вычислены по формуле

F = Рв.

Для описания деформированного состояния оболочки эритроцитов использовался потенциал Нео–Гука, заданный в одно-параметрической форме f ‘ = G ( х2+/.+х2 - з)2,                               (3)

где G - модуль сдвига G = ^р / h ; h - толщина эквивалентной оболочки. Значение упругой постоянной G в выражении (3) было определено с помощью численных экспериментов, в которых значения деформации эритроцита в зависимости от нагрузки сопоставлялись с экспериментальными значениями. Рассматривались эксперименты, в которых эритроцит деформировался малыми нагрузками при условии постоянства площади поверхности. Материал, обладающий упругим потенциалом Нео–Гука, является практически несжимаемым (коэффициент Пуассона равен ν = 0,5), поэтому выполняется условие XjX₂X₃ = 1. В случае деформирования эритроцита с постоянной площадью поверхности Х,Х₂ = 1, следовательно л₃ « 1, и выражение (3) принимает вид (2).

Определение упругой постоянной материала эквивалентной оболочки ЭРИТРОЦИТА G

Для определения параметра материала G в упругом потенциале Нео–Гука (3) были использованы два эксперимента: растяжение эритроцита лазерным пинцетом и аспирация с помощью микропипетки.

Растяжение оболочки эритроцита лазерным пинцетом

На рис. 2 показано, как происходит процесс растяжения эритроцита с использованием лазерного пинцета [22, 23]. Эритроцит помещают в раствор, осмотическое давление которого равно давлению внутри эритроцита, вследствие чего

Поперечный диаметр DT

Кремниевые микрошарики

Cпроектированный осевой диаметр DA Микрошарики закреплены на стекле и перемещаются с помощью микроскопа

а

Микрошарик в оптической ловушке б

Рис. 2. Растяжение эритроцита методом оптической лазерной ловушки: а – два кремниевых микрошарика диаметром 4,2 мкм присоединены к эритроциту (недеформированное состояние) (левый микрошарик приклеен к стеклу кюветы, в которой помещен эритроцит); б – деформированное состояние эритроцита [23]

мембрана эритроцита находится в недеформированном состоянии. К эритроциту присоединяют два кремниевых микрошарика диаметром 4,2 мкм. Один микрошарик жестко закреплен, другой, подвижный, захватывается лазерным пинцетом, и к нему прикладывается растягивающее усилие. В результате эксперимента получена зависимость растягивающего усилия от величины деформации (см. рис. 2).

Построение модели эритроцита выполнено оболочечными конечными элементами SHELL181 пакета прикладных программ ANSYS. Геометрическая модель эритроцита представлена 1/8 частью от исходной, ненапряженной формы оболочки эритроцита в виде дискоцита, форма которого (рис. 3) описывается выражением z0 = C2 (1 -p2)(C0 + C1P2 + C2P4), (4)

где p = r^, C = 0,86, Co = 0,01384083 , C = 0,2842917, C2 = 0,01306932, r0k гйк = 4,2 мкм; r0 - радиус параллельного круга [20]. Исходный диаметр дискоцита равен 8,4 мкм. Усилие, которое прикладывалось к модели, составляет четвертую часть от общего усилия, с которым растягивался эритроцит в эксперименте. При моделировании был выбран материал, обладающий Нео–Гуковским потенциалом (3).

Условия симметрии Условия симметрии

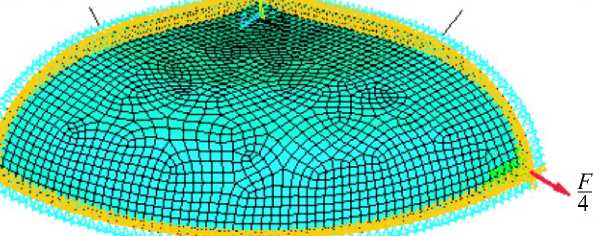
Условия симметрии

Рис. 3. Расчетная схема оболочки эритроцита, растягивающейся силой F

В результате расчета получено значение модуля сдвига G , равное 0,085 нН/мкм² (0,085 - 10^-4 дин/мкм²) для соответствующей эквивалентной оболочке толщиной 0,15 мкм. Жесткость при сдвиге для эквивалентной оболочки ц = G - h = 0,0128 мН/м (дин/см). Модуль упругости для эквивалентной оболочки E = 2(1 + v ) G = 3G , где коэффициент Пуассона v = 0,5. Жесткость при изгибе для эквивалентной оболочки равна D = Eh ³ /12 = 0,1 - 10^-12 мкН - м (0,1 - 10^-12 дин - см). Вычисленные значения осевого и трансверсального значений диаметров при найденных значениях G и D совпадают с экспериментальными [22] в пределах разброса экспериментальных данных (рис. 4, 5).

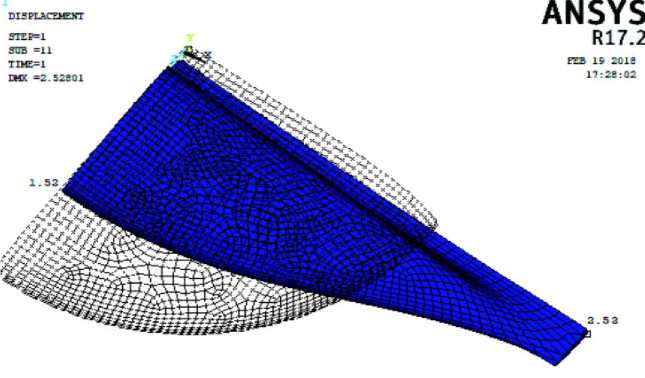
Рис. 4. Форма эритроцита, полученная при растяжении силой 100 пН. Перемещения относительно исходной формы даны в мкм

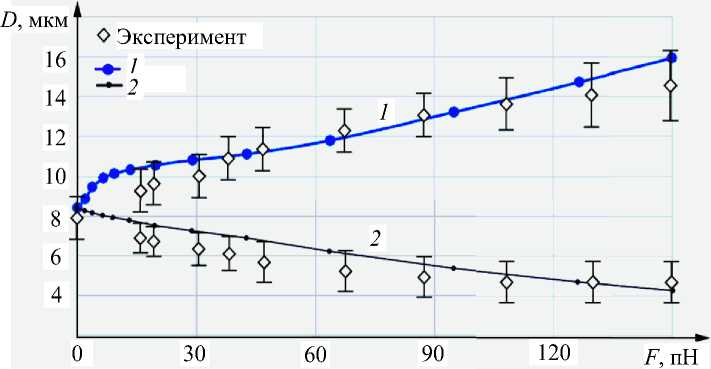
Рис. 5 График зависимости диаметров (1 – осевого DA; 2 – трансверсального DT) растянутого эритроцита от действующей силы;     – экспериментальные данные [22]

Расчет деформирования эритроцита при микропипеточной аспирации

В работе [19] жесткость при сдвиге ц эритроцита определяли методом микропипеточной аспирации путем всасывания ненапряженного эритроцита микропипеткой. К отверстию микропипетки с внутренним диаметром канала 1 мкм подсасывается эритроцит за счет отрицательного давления (EP). При определенном значении ДР он начинает втягиваться в канал микропипетки и образует «палец» (рис. 6). Измеряется ДР, длина втянутой части эритроцитаL и Rp - радиус канала пипетки. Возникшие меридиональные и окружные натяжения мембраны сосредоточены внутри пипетки и около ее устья, при этом их величина уменьшается обратно пропорционально квадрату расстояния от оси пипетки. Таким образом, в данном опыте с микропипеткой изучают собственные свойства мембраны вблизи конца пипетки независимо от внешней формы эритроцита. Для вычисления ДР в работе [20] предложена формула

Д Р = ^-

R P

2 L

R

—

1 I 1  2 L

1 + ln —

J     ^Rp

.

Построение модели эритроцита выполнено конечными элементами PLANE 183 – двумерными (2 D ) элементами объемного напряженно-деформированного состояния с восемью узлами ( ANSYS ). Геометрическая модель эритроцита представлена 1/2 от исходной (ненапряженной) формы оболочки эритроцита (рис. 7). К поверхности эритроцита внутри пипетки приложено отрицательное давление ДР . Контакт оболочки эритроцита с поверхностью пипетки осуществляется с помощью двумерных контактных элементов – типа контакта поверхности с поверхностью с тремя узлами CONTA 172, которые принадлежат деформируемой поверхности оболочки и двумерных ответных элементов TARGE 169, принадлежащих абсолютно жесткой поверхности микропипетки. Коэффициент трения о стенки микропипетки в программе задан равным нулю, так как в работе [20] показано, что эффекты трения практически

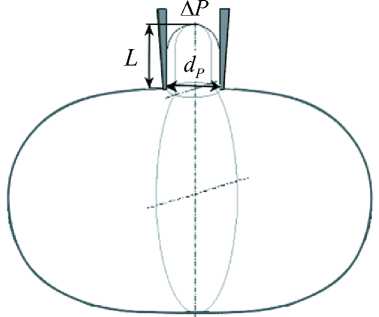
Рис. 6. Схема измерения длины втянутой части эритроцита, возникающей под действием всасывающего давления ДР

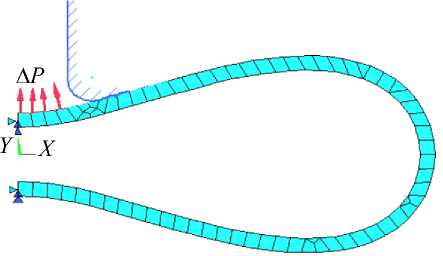
Рис. 7. Расчетная схема эритроцита, находящегося под действием отрицательного давления гидравлической микропипетки

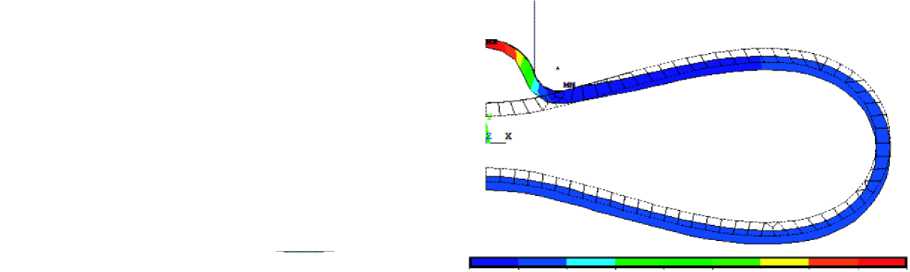
0  0,08 0,17 0,25 0,34 0,42 0,50 0,59 0,67 0,75

Рис. 8. Перемещения мембраны эритроцита (мкм) под действием всасывающего давления 40Па (400 дин/см ² )

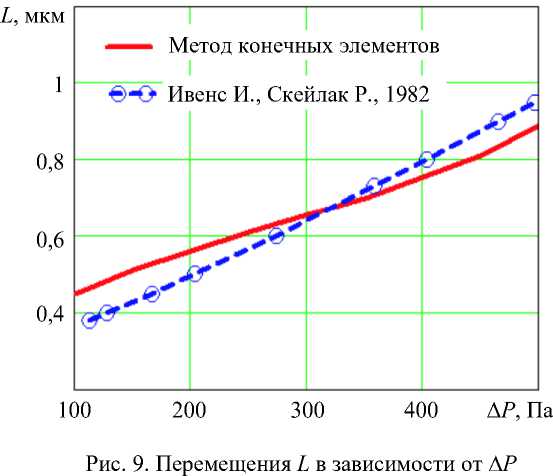
отсутствуют. В результате расчета получено значение модуля сдвига G , равное 0,085 ⋅ 10^–4 дин/мкм² (0,085 нН/мкм²) для соответствующей эквивалентной оболочки толщиной 0,15 мкм. С помощью составленной конечно-элементной модели была вычислена длина втянутой части оболочки эритроцита L под действием отрицательного давления Δ P (рис. 8). Значения зависимости L от Δ P совпадают с экспериментом и результатами вычислений по формуле (5) с точностью 5–10 % в случае, если эквивалентная оболочка толщиной 0,15 мкм имеет жесткость при сдвиге µ = G ⋅ h = 0,0128 мН/м (дин/см) (рис. 9).

Расчетная схема

Расчетная схема агрегации эритроцитов представлена на рис. 10. Расчет процесса деформирования оболочки эритроцита при микропипеточной аспирации выполнен методом конечных элементов (МКЭ) c помощью пакета прикладных программ ANSYS.

Разрешающие уравнения МКЭ могут быть получены минимизацией полной энергии системы П:

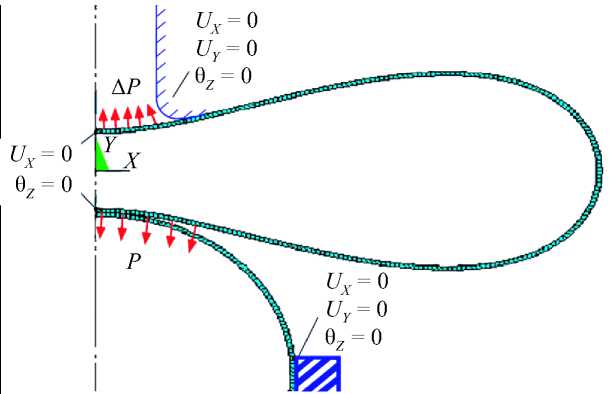
Рис. 10. Расчетная схема

δЭ=δU+δU -δV =0, где U – потенциальная энергия деформации; U – потенциальная энергия контактной зоны взаимодействия; V – работа внешних сил.

Приращение потенциальной энергии деформации системы контактирующих тел (оболочек эритроцитов) имеет вид

δ U = ∫∫∫ σδε dV ,

V где σ – вектор напряжений; ε – вектор деформаций; V – объем элемента.

В качестве конечных элементов оболочки эритроцита использованы гиперупругие конечные элементы c возможностью больших деформаций и перемещений. Контактная зона, охватывающая контактную поверхность, делится на ряд контактных элементов. Элемент представляет собой взаимодействие между поверхностным узлом одного тела с соответствующей поверхностью элемента другого тела. Приращение потенциальной энергии контактной зоны взаимодействия площадью S рассчитывается следующим образом:

8 U_K = JJ p 8 u_ndS + JJ t8 u_tdS ,

SS где u – величина контактного зазора в направлении нормали к поверхности, u – величина контактного зазора в тангенциальном направлении, P – контактное давление в направлении нормали к поверхности, которое равно нулю; p = 0, если ип > 0; PК = Knun, если ип < 0; Кп - матрица жесткости контактной поверхности; т -фрикционное напряжение.

Были вычислены формы участков оболочки ненапряженного эритроцита внутри и вне пипетки. Использованы экспериментальные данные: всасывающее давление Δ P = 20 Па (200 дин/см²), длина втянутой части эритроцита L = 0,5 мкм и радиус канала пипетки R = 1 мкм [19], радиус сферического эритроцита, сильно втянутого в пипетку, R = 3 мкм.

Согласно модели обедненного слоя в контактирующем слое возникают два типа напряжений:  нормальные и касательные. Нормальные напряжения являются результатом притяжения контактирующих поверхностей. Чем больше контактные напряжения притяжения, тем больше площадь агрегации эритроцитов. При задании контактного давления притяжения в зоне агрегации в пакете программ ANSYS используется технология Fluid Penetration Pressure. Расчет контакта производился методом итераций. Точки поверхности подвергались воздействию контактного давления, если контакт был открыт. Если контакт закрывался, то контактному давлению подвергались последующие точки. По мере увеличения зоны агрегации ненапряженный эритроцит наползал на жестко закрепленный, а его оболочка в зоне, примыкающей к зоне контакта, натягивалась. Процесс расчета завершался, когда энергия деформации уравновешивала работу агрегации.

Нормальные напряжения определялись путем сопоставления расчетного размера поверхности контакта с экспериментальным значением.

Оценка сдвиговых напряжений, возникающих при агрегации эритроцитов

Предположим, что движение слоя жидкости между контактирующими эритроцитами, помещенными в раствор макромолекул, происходит по закону Куэтта, тогда касательные напряжения τ можно также вычислить по формуле

τ = η u / h ,

где η – вязкость; u – скорость слоев жидкости; h – толщина прослойки жидкости между контактирующими эритроцитами.

Межклеточное расстояние между агрегированными эритроцитами, измеренное с помощью сканирующего микроскопа, примерно равно диаметру молекул декстрана [24]. Экспериментально установлено, что на поверхности гликокаликса (наружный слой эритроцитов) адсорбируются различные макромолекулы, в частности декстран [3]. Границы слоя жидкости между поверхностями становятся неровными, поэтому эффективную толщину слоя движущейся жидкости в первом приближении можно принять равной h = d – ( d – p ) = p , где d – диаметр молекулы декстрана с молекулярной массой 500 кДа, d = 29,4 ÷ 30 , 2 нм [25], р – глубина проникновения полимерных молекул в слой гликокаликса [13], р = 5 нм (рис. 11).

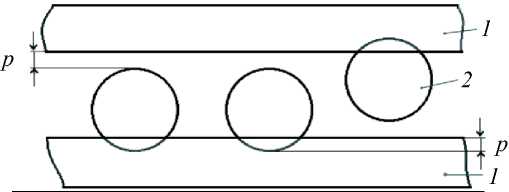
Рис. 11. Схематичное изображение слоев гликокаликса ( 1 ) с адсорбированными макромолекулами ( 2 )

Верхнюю границу значений касательных напряжений определяют критические сдвиговые напряжения, останавливающие агрегацию, экспериментальное значение которых равно примерно 0,25 Па для раствора декстрана с молекулярной массой 80 кДа [26]. В работе [27] были измерены параметры агрегации эритроцитов, где изучали процесс, при котором два эритроцита самопроизвольно «наползают» друг на друга после образования локального контакта без влияния сторонних сил. Была измерена скорость u спонтанной агрегации. По формуле (6) можно вычислить сдвиговые напряжения в растворе декстрана 500 кДа, которые составили τ = 0,06 ÷ 0, 07 Па при экспериментальных значениях η раствора NaCl, η = 1,0 ÷ 1,1 ⋅ 10 ^{- 3} Па·с [28], u = 0,3 мкм/с [24], h = р = 5,0 нм [13].

С помощью лазерных пинцетов были измерены параметры дезагрегации. Два эритроцита соединяли с помощью лазерных пинцетов в агрегат и измеряли силу, которую нужно приложить для разделения эритроцитов (рис. 12, а ). Она была измерена в зависимости от площади перекрытия S [27]. Экспериментально установлено, что эритроциты при дезагрегации движутся параллельно, поэтому силу взаимодействия можно вычислить по формуле

FD =τ S . (7)

Зависимость (7) следует из условия равновесия сил, действующих на эритроцит (рис. 12, а, б). Вычисленные по формуле (7) усилия дезагрегации эритроцитов FD в растворе декстрана с молекулярной массой 80 кДа составили FD80 = 2,5 пН при площади взаимодействия S = 10,0 мкм2 и при критическом сдвиговом напряжении τ=0, 25 Па, что близко к экспериментальному значению усилия дезагрегации эритроцитов FD в растворе декстрана с молекулярной массой 500 кДа FD500 = 2,0 пН [24] при той же площади взаимодействия S = 10,0 мкм2. Тогда критические сдвиговые напряжения для декстрана с молекулярной массой 500 кДа можно вычислить по формуле (7):

τ c 500 = FD 500 / S = 0,2 Па.

Иcходя из приведенных выше рассуждений можно предположить, что значение критического сдвигового напряжения, останавливающего агрегацию эритроцитов в растворе декстрана с молекулярной массой 150 кДа τ = 0,25, лежит в пределах 0,2 ÷ 0,25 Па. Сдвиговые напряжения при агрегации не превышают критических значений и составляют 0,06 ÷ 0, 07 Па.

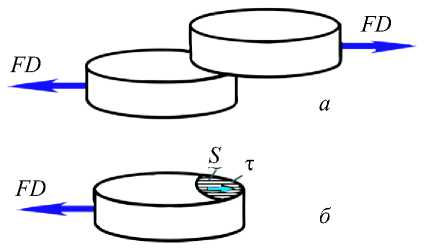
Рис. 12. Схема взаимодействия эритроцитов при дезагрегации ( а ); расчетная схема для силы дезагрегации ( б )

Допущения

При расчете были приняты следующие допущения:

– Закрепленный эритроцит имеет сферическую форму. При большом натяжении ( Т > 20 мкН/м) его упругие свойства определяются выражением (1), в котором µ = 0, а K = 500 мН/м.

– Согласно [20] трением между стенкой пипетки и оболочки эритроцита можно пренебречь.

– Касательные напряжения между поверхностями агрегирующих эритроцитов равны 0,07 Па.

Граничные условия

– В точках эритроцитов на оси симметрии – условия симметрии:

u = 0 – перемещения вдоль оси Х равны 0;

θ = 0 – угол поворота относительно оси z равен 0.

– Эритроцит сферической формы жестко закреплен в удерживающей пипетке, поэтому перемещения и угол поворота в этих точках равны нулю: u = 0, u = 0, θ = 0 (см. рис. 10).

– Точки пипетки закреплены: u = 0, u = 0, θ = 0 (см. рис. 10).

Результаты

С помощью построенной конечно-элементной модели был выполнен расчет напряженно-деформированного состояния парного агрегата эритроцитов под действием давления притяжения p и всасывающего давления Δ P со стороны пипетки на ненапряженный эритроцит. Вычисленная длина втянутой части оболочки ненапряженного эритроцита L = 0,5 мкм совпадает с экспериментальным значением

0,5 мкм в работе [19] при заданном A P = 20 Па (рис.13). Сферический эритроцит практически не деформируется. Под действием контактного давления притяжения P ненапряженный эритроцит притягивается к жестко закрепленному сферическому эритроциту. При P = 3 Па высота контактной зоны L = 1,35 мкм (см. рис. 13), что близко к экспериментальному результату 1,3 ^ 1,5 мкм [19]. Вычисленная в работе плотность упругой энергии деформации в зоне агрегации двух эритроцитов изменяется от 4,7 10^–3 мкДж/м² в точках на оси симметрии до 2,4 10^–3 мкДж/м² в крайних точках контактной зоны (рис. 14). Таким образом, среднее значение плотности упругой энергии деформации составляет 3,0 10^–3 мкДж/м², что соответствует результату

3,0 10–3 мкДж/м2 работы [19].

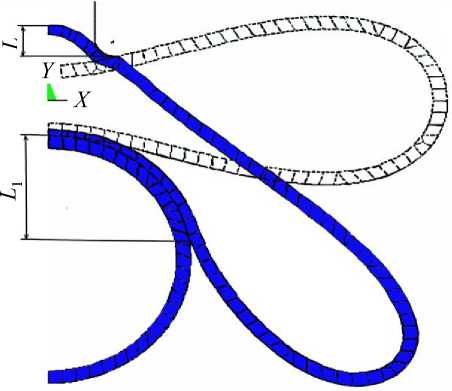
Рис. 13. Деформирование эритроцита при агрегации ( Р = 3 Па)

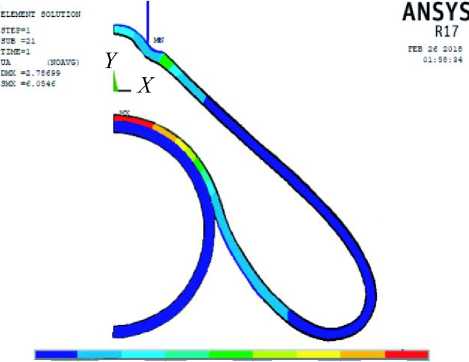
0 0,67 1,35 2,02 2,69 3,36 4,04 4,71 5,38 6,05

Рис. 14. Плотность упругой энергии деформации (мкДж/м2) (10–3 эрг/см2)

Обсуждение

Получено значение давления притяжения, возникающее при агрегации эритроцитов, P = 3 Па путем сопоставления результатов расчета деформированного состояния одиночных эритроцитов при образовании парного агрегата в трехпроцентном растворе декстрана с молекулярной массой 150 кДа с результатами эксперимента [19]. Согласно модели обедненного слоя давление притяжения имеет осмотическую природу и может быть вычислено согласно закону Вант-Гоффа П = RT A C, тогда разность концентраций A C , создающая P = 3 Па, равна 1,3 •IO^-6 моль/л. Полученное значение A C на два порядка ниже концентрации трехпроцентного раствора декстрана 150 кДа, равной 7,5·10^–4 моль/л для 3%-ного раствора.

Так как макромолекулы декстрана адсорбируются на поверхности гликокаликса, величина осмотического давления П уменьшается на величину осмотического давления этих адсорбирующихся молекул декстрана. В работах [29, 30] показано, что остальные виды взаимодействия: стерическое отталкивание и Ван-дер-Ваальсово взаимодействие (порядка 10^–2 мкДж/м²) несущественны, и ими можно пренебречь. При увеличении концентрации раствора макромолекул значение давления притяжения эритроцитов увеличивается, и, соответственно, увеличивается площадь контакта.

При агрегации эритроцитов, находящихся в растворе макромолекул в нативном состоянии, перемещение эритроцитов происходит параллельно площадкам контакта (см. рис. 12). При этом контактное давление притяжения не влияет на силу агрегации, которая равна произведению касательного сдвигового напряжения на величину площади контакта эритроцитов. При дезагрегации касательные сдвиговые напряжения возрастают до критических значений. При этом контактное давление притяжения и площадь контакта не изменяются, а следовательно, сила дезагрегации увеличивается по сравнению с силой агрегации, что наблюдалось в экспериментах [24].

Заключение

Разработана математическая модель агрегации двух эритроцитов с использованием численного метода конечных элементов. Выполнен анализ напряженного состояния, возникающего в площадке контакта двух эритроцитов при их агрегации. С помощью разработанной модели выполнен расчет формоизменения эритроцитов при агрегации в эксперименте с микропипетками.

Анализ напряженного состояния в зоне контакта эритроцитов при агрегации показал, что величина площади контакта зависит от величины нормальных напряжений притяжения: чем больше значения нормальных напряжений, тем больше площадь контакта. Величина нормальных напряжений притяжения эритроцитов составила порядка 3 Па в трехпроцентном растворе декстрана с молекулярной массой 150 кДа. Величина касательных напряжений вязкого сопротивления составила 0,06 ^ 0,07 Па в растворе декстрана с молекулярной массой 150 ^ 500 кДа. Усилие дезагрегации FD (или агрегации FA ) равно (рис. 15):

FD = PS cos а + т S sin а .

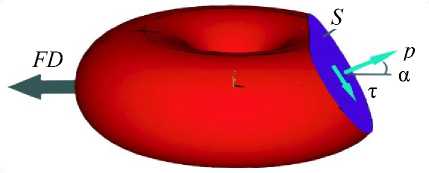
Рис. 15. Силовые факторы, действующие на эритроцит при дезагрегации: FD – сила дезагрегации; p – нормальные напряжения притяжения и τ – касательные сдвиговые напряжения, действующие в площадке контакта S

Благодарности

Автор выражает благодарность сотрудникам кафедры общей физики и волновых процессов МГУ им. М.В. Ломоносова и лаборатории лазерной биомедицинской фотоники к.ф.-м.н. А.В. Приезжеву, д.ф.-м.н. С.Ю. Никитину, А.Н. Семенову, А.Е. Луговцову, К. Ли за обсуждение работы.