Численное моделирование процесса обледенения в условиях крупных переохлажденных капель

Метеорологические условия обледенения могут стать причиной недопустимого ухудшения аэродинамических характеристик летательных аппаратов (ЛА). Несущие аэродинамические поверхности летательных аппаратов и поверхности управления воздушным судном подвержены воздействию обледенения. Одним из существенных параметров, определяющих интенсивность роста льда и его локализацию, является размер капель, выпадающих на обледеневающую поверхность. Поскольку в атмосферных облаках содержатся капли различного диаметра, то в качестве обобщенной характеристики спектрального распределения размеров капель принято использовать понятие среднего медианного диаметра MVD. Масса воды, содержащаяся в каплях диаметром больше MVD, равна массе воды, содержащихся в каплях диаметром меньше MVD. Как правило, существующие системы защиты ЛА от воздействия условий обледенения рассчитаны на предотвращение опасного обледенения при попадании в облака, содержащие мелкодисперсионные капли размером MVD = 20 мкм.

Однако, расследование катастрофы самолета ATR-72 близ Роузлоуна, штат Индиана, 31 октября 1994 года [1] , пробудило повышенное внимание к метеорологическим исследованиям, показавшим, что существующие в атмосферных облаках крупные переохлажденные капли (SLD — Supercooled Large Droplets) с размером MVD существенно выше 20 мкм (до 400 мкм) стали причиной обледенения, вызвавшего потерю управления. Наросты льда, возникающие в условиях SLD, могут привести к чрезвычайно серьезному ухудшению летно-технических характеристик самолета, включая: уменьшение угла сваливания, сопровождающееся увеличением скорости сваливания; снижение подъемной силы более чем на 60% и увеличение лобового сопротивления до 200%. Указанные явления могут критическим образом влиять на безопасность полетов, поэтому при проектировании противообледенительных систем необходимо использовать расчетные методы для предотвращения недопустимого ухудшения аэродинамических характеристик элементов летательного аппарата [2] .

Атмосферные облака SLD могут состоять как из переохлажденной измороси «freezing drizzle», так и из переохлажденного дождя «freezing rain». Динамика этих капель имеет свои особенности [3]. Капли большого размера SLD двигаются по баллистическим траекториям, вследствие чего их выпадение на аэродинамические поверхности происходит ниже по течению от областей, защищенных противообледенительными системами, что приводит к потенциально неконтролируемому процессу образования льда на незащищенных поверхностях. Динамику крупных капель необходимо учитывать при вычислительном моделировании обледенения при проектировании систем противообледенительной защиты и в процессе сертификации авиационной техники.

Таким образом, при разработке мер противообледенительной защиты нужно располагать расчетными инструментами, позволяющими оценивать эффективность защиты элементов авиационной техники от воздействия условий обледенения. Для этого необходимо моделировать процессы движения подобных капель в несущем воздушном потоке, процесс их взаимодействия с поверхностью ЛА и процесс формирования льда. Существующие программные комплексы, такие как ПК Ansys Fensap-Ice UR L 1 и ПК Flowvision URL компании ООО «ТЕСИС», обладают недостаточной точностью расчета ледяных наростов сложных форм. Кроме того, зарубежные ПК, такие как Ansys Fensap-Ice URL , требуют импортозамещения. С целью устранения существующего пробела в процессе моделирования крупных переохлажденных капель выполнено усовершенствование ПМ Кристалл [4] путем разработки математической модели обледенения в условиях SLD.

Решение поставленной задачи проводилось в следующих направлениях.

Во-первых, решение проблемы течения капель в несущем потоке до их взаимодействия со стенкой. Эта проблема включает в себя моделирование полей течений двухфазного дисперсного потока в постановке Эйлера и отработка методических проблем расчета величин коэффициентов улавливания капель для спектра размеров SLD. Данная проблема была решена путем использования ПМ Лазурит [5] , что позволило рассчитывать поля течений двухфазного дисперсного потока в постановке Эйлера и определять величины коэффициентов улавливания капель для спектра размеров капель, характерных для SLD.

Во-вторых, решение проблемы взаимодействия крупных капель с твердыми поверхностями объекта и ледяного нароста. Они включают в себя вопросы моделирования процесса формирования облака вторичных капель с учетом их термодинамического состояния, а также влияние этих капель на результирующий коэффициент улавливания и на процесс формирования льда.

1.    Метод расчета формирования льда в условиях крупных переохлажденных капель 1.1.    Термодинамическая модель нарастания льда

Описание термодинамических процессов обледенения в условиях SLD основывается на двух моделях: Мессинжера [6] и течения жидких водяных пленок SWIM (Shallow Water Icing Model) [7]. В работе [8] с использованием указанных моделей получена система дифференциальных уравнений переноса с источниковыми членами.

Уравнение сохранения массы

ρ _w

∂h _w

~t^ --+ — (u w h w )

— mimp   m ice   m es   m film sched

представляет собой баланс массовых скоростей потоков воды в контрольном объеме на поверхности льда:

ρw ∂∂htw — втекающих и вытекающих из контрольного объема, pw — (uwhw) — накапливающихся в контрольном объеме, mimp — выпадающих на поверхность капель, rnice — замерзающей воды, rnes — покидающих контрольный объем в результате испарения или сублимации, mf ilm sched — срывающихся с поверхности пленки. _

В уравнении (1)

ρw — плотность воды (кг/м3), hw — высота пленки воды (м), uw — средняя по сечению пленки скорость течения воды по поверхности льда (м/с), t — время (с).

Аналогично уравнение сохранения энергии записывается в виде:

∂h w C p,w T ρ w     ∂t

+ ^р w • ^(u w ^h w ^C p,w T )

Q kin + Q ice

Q imp

АЛЛ   Л

Q es Q rad   Q conv   Q film sched + Q

В уравнении (2) T — температура:

при T < 0 ° C — температура поверхности льда или сухой поверхности, при T > 0 ° С — температура водяной пленки или сухой поверхности, при T — 0 ° С — температура поверхности льда, водяной пленки или сухой поверхности.

Первый член в левой части уравнения (2) представляет собой изменение энтальпии воды, находящейся в контрольном объеме. Второй член левой части выражает разность энтальпий втекающей и вытекающей воды.

Указанные тепловые потоки уравновешиваются в правой части уравнения суммой следующих потоков:

Q ki _n — кинетической энергии выпадающих капель воды,

Q ice — фазового перехода (замерзание воды / плавление льда) и охлаждения льда,

Q _imp — охлаждения выпадающих капель воды,

Q _es — испаряющейся/сублимирующейся воды,

Q _rad — излучения,

Q _conv — конвекции,

Q f _{ilm sched} — охлаждения за счет срывающихся с поверхности пленки капель воды,

Q h _eat — поток тепла на дне контрольного объема.

Массовая скорость потока капель, остающихся на поверхности после выпадения на нее, находится из уравнения mimp  Utt • LWC ^drops

• 1 - m m0

где

U _∞ — скорость потока воздуха (м/с),

LWC — Liquid Water Content, водность потока, равная массовому содержанию воды в потоке воздуха (кг/м ³ ),

βdrops — коэффициент улавливания капель, mms — коэффициент потери массы, m0 — масса капель, претерпевших соприкосновение с поверхностью (кг/(м2с)), ms — масса капель, претерпевших отскок или расплескивание (кг/(м2с)).

Использование коэффициента улавливания капель β _drops позволяет рассчитать количество всех капель, претерпевающих столкновение с поверхностью льда. При этом не учитываются эффекты образования вторичных капель. При расчете обледенения в условиях SLD нельзя пренебречь эффектами, связанными с отскоками и расплескиванием капли в процессе ее взаимодействия с поверхностью. Последний член произведения в данном уравнении 1 — m s позволяет учесть массовую m 0

долю капель, остающихся на поверхности после столкновения и не претерпевающих отскок или расплескивание. Для расчета величины этого члена, характеризующего коэффициент потери массы, необходимо разработать соответствующие физические и математические модели.

• 1.2.    Физическая модель взаимодействия крупных капель с поверхностью

В работе [9] выполнен качественный анализ влияния различных эффектов динамики крупных капель на процесс численного моделирования процесса обледенения. Выполнена классификация этих эффектов на три категории (эффекты первого, второго и третьего порядка) на основе их влияния на процесс выпадения капель на стенку.

Эффекты первого порядка — это взаимодействие капли со стенкой, которое возникает, когда капля, столкнувшаяся со стенкой, вся или частично отскакивает обратно в несущий поток. Эффекты второго порядка включают распад капель, при этом капли подвергаются деформации под действием аэродинамических сил, распадаются на мелкие вторичные капли. Другие физические эффекты динамики крупных капель, такие как гравитационные эффекты и эффекты турбулентности, считаются эффектами третьего порядка и пренебрежимо малы.

Исходя из результатов указанного анализа, при разработке модели обледенения в условиях SLD рассматриваются эффекты первого порядка: взаимодействие крупной капли со стенкой.

Варианты взаимодействия крупных капель SLD с поверхностью объекта представлены на рисунке 1:

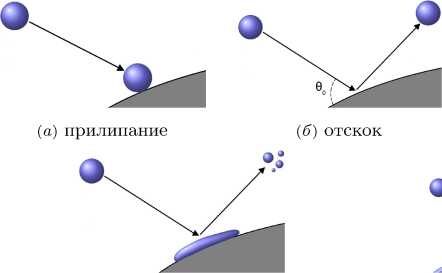
( г ) разбрызгивание и частичное прилипание к сухой поверхности

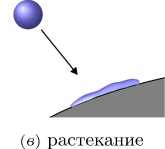
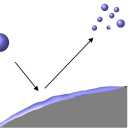
( Д ) разбрызгивание на смоченной поверхности

Рисунок 1. Варианты взаимодействия капли с поверхностью

Из рассмотрения вариантов, представленных на рисунке 1, следует, что не все выпадающие капли остаются на поверхности, поэтому следует уточнить величины коэффициентов улавливания путем корректного моделирования процесса их взаимодействия с поверхностью ледяного нароста.

• 1.3.    Математическая модель взаимодействия крупных капель с поверхностью

В соответствии с данными [10 , 11] режимы, представленные на рисун ке 1, задаются числом Вебера для капли

We = ρair · u2n,0 · MWD · 10-6 d                   σ, где

ρair — плотность воздуха (кг/м3), un,0 — составляющая скорости капли, нормальная к поверхности профиля (м/с),

MVD — средний медианный диаметр капли (мкм),

σ — коэффициент поверхностного натяжения воды (Н/м).

При W e _n ⩽ 2 реализуется прилипание капли к поверхности (рису нок 1а) и ее дальнейшее участие в процессе льдообразования.

При 2 < We n ^ 10 реализуется отскок капли (рисунок 1б, происходит ее участие в формировании вторичного потока частиц. Осаждение на поверхность отсутствует, результирующий коэффициент улавливания принимается нулевым.

Для расчета скоростных характеристик капли, претерпевшей отскок, используются следующие соотношения:

u t,s = 5

u t, 0      7,

u fu,n = un,s = - 0,993 - 1,76 · θ0 + 1,56 · θ02 - 0,49 · θ03 , un,0

где fu,t> fu,n — отношение тангенциальной и нормальной составляющих скоростей, связанное с отскоком частицы от твердой поверхности, ut,o, un,0 — тангенциальная и нормальная к поверхности составляющие вектора начальной скорости капли ud (м/с), uts, un,s — тангенциальная и нормальная к поверхности составляющие вектора скорости капли после удара ud,s (м/с),

θ ₀   — угол падения капли в радианах.

При W e n > 10 и K y ⩽ K y,crit — реализуется растекание капли по поверхности ( рисунок 1в) , то есть полное улавливание. K y — параметр разбрызгивания Ярина и Вейсса [12] вычисляется по формуле:

(3)              Ky = 3 3 / LWC \ 8   /    2     \ 16 2   ρair      · Oh-5Wen    , где

Oh =

µ air

√ ρ air · σ · M W D ·10 ^{- 6}

— критерий подобия Онезорге,

µ _air — динамическая вязкость жидкости (Па · с),

W e _n — число Вебера, построенное на компоненте скорости капли, нормальной к поверхности профиля.

При K y > K y_,cri_t происходит разбрызгивание или частичное прилипание капли, которое может реализовываться как на сухой (рисунок 1г) , так и на влажной (рисунок 1д) поверхности.

Варианты прилипание рисунок 1а и растекание рисунок 1в не представляют трудностей для расчета, поскольку не требуют корректировки коэффициента улавливания. Вариант отскока рисунок 1б приводит к обнулению коэффициента улавливания, но требует корректировки параметров отскочивших капель. Наибольшую трудность представляют варианты рисунок 1г и рисунок 1д, при которых происходит лишь частичное прилипание, а отскочившие капли образуют вторичный поток.

При взаимодействии с сухой поверхностью (рисунок 1г расчет количе- ства, массы и скорости вторичных капель выполняется с использованием модели Трухильо [13]. Указанная модель применима при расчете форм ледяных наростов в режиме «rime ice». Данный режим характеризуется полным замерзанием выпадающих капель и отсутствием пленки жидкой воды на поверхности ледяного нароста. Учет массы капель, разбрызгивающихся при ударе о поверхность аэродинамического профиля выполняется с применением коэффициента потери массы ϕ, который рассчитывается по формулам (4).

ф ( К _у ) = 3 ,8- ( 1 — e ^{0 , 85( K y K y},c^{rit )} ^ K y

ф ( К у ) = 0, при K y <  K y,c_nt = 17

при K y > K y,crit = 17

где параметр K y рассчитывается по формуле (3) .

Количество вторичных капель может быть определено с использованием эмпирической модели Трухильо [13] :

где

N =^f0,0437 [k ( ) — K crit

22 у [  \(u_d,n)J

44,92

)

K = Oh 5 • We n — параметр Коассали,

K _crit — критический параметр Коассали, который может быть рассчитан на основании уравнения (3) , где

Ky < Kcrit = 17, а n — единичный вектор нормали к поверхности в месте выпадения капли.

Параметр Коассали K связан с параметром разбрызгивания Ярина и

Вейсса K y формулой (3) K y =

3 ( lwc \ ⁸

2    ρ air

K 1⁵6 .

Зная количество вторичных капель (5) и величину потери массы (4) , диаметр вторичных капель может быть рассчитан из соотношения:

ds (Й

d 0 ,

где d 0 и d _s — диаметры первичных (выпадающих на поверхность) и вторичных (отскочивших от поверхности) капель, мкм.

Вектор средней скорости вторичных капель u d_,s (м/с) также определяется с использованием эмпирической модели Трухильо [13] следующим образом:

• (6)                 (u dsj ) = o,_{85 +} 0,0025 _Arctg (ud,^ ,

(u d ,t)                             ^{( u} d ^{,n )}

• (7)                 (ud^n) = 0,12 ₊ 0,002Arctg ⁽u ^{d ,t} ,

(u d ,n)                            (u d ,n)

где t — единичный вектор, направленный по касательной к поверхности в месте выпадения капли.

В уравнениях (6) , (7) угол падения капли, от которого зависит вторичная скорость капель, представлен в виде нормальной и тангенциальной составляющей.

Кроме взаимодействия капель с твердой сухой стенкой, указанного на рисунке 1г , на практике может реализовываться вариант рисунок 1д . Наличие на поверхности жидкой пленки воды, как отмечается в работе [10], оказывает значительное влияние на процесс разбрызгивания. Режим обледенения «glaze ice» наблюдается в условиях относительно высоких температур внешнего потока и характеризуется наличием жидкой пленки воды на поверхности льда.

В зависимости от условий обледенения, пленки воды могут иметь значительную толщину. Наличие жидкости на поверхности может играть существенную роль, поскольку разбрызганные капли могут увлекать жидкость из пристеночной пленки [10] , что наблюдалось экспериментально в работе [14] . При этом указывается, что масса разбрызганной моды может даже превосходить массу падающей капли. Для учета эффектов, связанных с выпадением капель на влажные поверхности, использована модель Саменфинк [15] . В данной модели разбрызгивание наступает при величине параметра S > 1, который определяется формулой:

Re d

S    24 • Lad,419 ’ где

Re d

La d ν d µ d

u n,s · d 0 ·10 ^{- 6}

=       _{ν d}      ,

= ρ d · σ · d 0 ·10 ^{- 6}

µ ² _d        ,

— кинематическая вязкость жидкости (Па · с), — динамическая вязкость жидкости (Па · с).

Следует заметить, что при расчете параметра S используется число Лапласа, построенное с использованием плотности и вязкости воды. Согласно рекомендациям работы [15] , это позволяет учесть эффекты расплескивания капель на влажной поверхности.

Характеристики вторичных капель определяются следующими формулами.

Диаметр вторичных капель d _s по отношению к диаметру первичных капель d 0 :

^{d s} = 1 - 0,03454 · S ^{0 , 175} · θ 0 ^{0 , 1239} · La ⁰ d^{, 265} .

d 0

Скорость вторичных капель u _s (м/с) по отношению к скорости первичных капель u d (м/с):

^{u s} = 0,08214 · S ^{- 0 , 3384} · θ 0 ^{0 , 2936} · δ ^{- 0 , 3113} · La ⁰ _d ^{, 1157} .

Угол отскока капель:

θ _s = 2,154 · S 1 , 0946 · θ ₀0 , 03389 · δ -0 , 1589 .

Нормальная u _n,s (м/с) и тангенциальная u t_,s (м/с) составляющие скоростей вторичных капель:

u n,s = u d,s ·sin ^{π · θ s} , 180

u t,s = u d,s

· cos

π · θ s 180 ^.

Коэффициент потери массы рассчитывается по формуле:

f m Sp = ^{m s} = 0,0866 · (S - 1) ^{0 , 3188} · θ 0 ^{0 , 1223} · δ ^{- 0 , 9585}

Количество образовавшихся вторичных капель рассчитывается по формуле (5) .

Представленные выше модели Трухильо и Саменфинк позволяют описать процесс разбрызгивания одиночной первичной капли размером d 0 , выпадающей на поверхность. Расчетный анализ реальных спектров размеров капель, получаемых после разбрызгивания в процессе стендовых испытаний или при полетах в атмосферных облаках, может быть выполнен двумя способами:

• (1 )    Во-первых, весь спектр капель разделяется на несколько диапазонов размеров [d ₀ ,i -1 ,d ₀ ,i ] и расчет разбрызгивания выполняется для каждого диапазона, а далее полученные результаты суммируются.

• (2)    Во-вторых, расчет может выполняться с использованием среднего медианного диаметра MVD определение которого дано во введении.

Дальнейшие анализы проводятся с использованием MVD.

Анализ моделей разбрызгивания, представленный в работе [9] , показывает, что обе модели Трухильо [13] и Саменфинк [15] показывают хорошие результаты при валидации с экспериментальными данными в диапазоне скоростей до 78 м/c. В соответствии с выводами данной работы предпочтение было отдано модели Трухильо на том основании, что данная модель демонстрирует примерно аналогичные результаты по разбрызгиванию для капель с размером MVD = 92 мкм и MVD = 236 мкм, и результаты могут быть экстраполированы за пределы экспериментальных данных (на диапазон повышенных скоростей). При возрастании скорости выпадающих капель величина коэффициента потери массы, рассчитанная с использованием модели Трухильо, постепенно снижается (кривая 1 на рисунке 2) , что не противоречит выводам работы [9] .

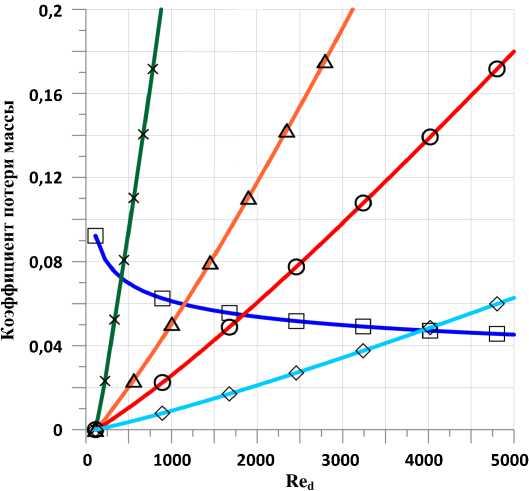
Рисунок 2. Коэффициент потери массы, рассчитанный по различным моделям

Саменфинк, высота пленки

10 мкм

50 мкм

100 мкм

300 мкм

Трухильо

При этом отмечено, что модель Саменфинк при указанном выше

298 А.В. Горячев, П.А. Горячев, Д.А. Горячев, М.В. Нуриев, А.А. Николаев, А.A. Рыбаков увеличении размеров капель демонстрирует более высокие величины потери массы, что по мнению авторов [9] не представляется реалистичным. Рисунок 2 показал, что расчетные величины коэффициента потери массы с использованием модели Саменфинк неограниченно возрастают при увеличении скорости капель. Из сопоставления характера кривых на нём следует, что результаты расчета с использованием модели Трухильо лучше соответствуют экспериментальным данным в области высоких скоростей капель.

С другой стороны, при снижении скорости потока капель (область Re d < 500 на рисунке 2) наблюдается значительный рост расчетных величин коэффициента потери массы, рассчитанных с использованием модели Трухильо. Это не соответствует экспериментальным данным, поскольку в этой области должно наблюдаться прилипание капель (рисунок 1а) или их растекание по поверхности (рисунок 1в) . В этой области результаты расчетов по модели Саменфинк на рисунке 2 представляются более реалистичными и более соответствующими экспериментальным данным.

Для преодоления указанных недостатков в данной работе предлагается объединение обоих моделей с использованием формулы:

m

• ⁽⁸⁾                       --- = minfmsp , Ф^(КУ)) .

2.    Особенности реализации ПМ Кристалл

m ₀

Графически данное объединение двух моделей представлено на рисун ке 2. Результирующая кривая, имеет экстремум в точке пересечения кривых f m _Sp и Ф(К _у ), что соответствует физическим особенностях процессов, протекающих по сценариям, приведенным на рисунке 1 . Использование формулы (8) позволяет учитывать особенности взаимодействия капель с сухими и смоченными поверхностями, моделировать эффекты прилипания и растекания капель при минимальных скоростях и избежать чрезмерного повышения коэффициента потери массы в широком диапазоне скоростей выпадающих капель.

Согласно уравнению (8) , коэффициент потери массы при разбрызгивании на графике рисунок 2 определяется минимумом из значений, полученных по модели Трухильо и значений, полученных по модели Саменфинк для различных толщин пленки воды на поверхности. Такой подход позволяет избежать чрезмерного возрастания разбрызгивания, предсказываемого как моделью Трухильо в области малых величин чисел Re d , так и моделью Саменфинк в области больших Re d .

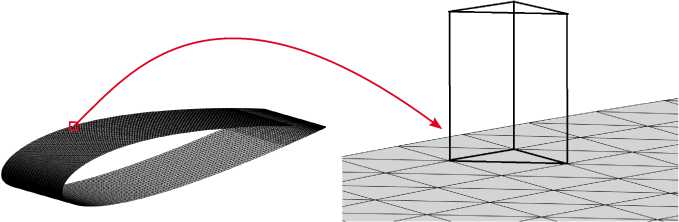
При решении уравнений (1) , (2) используется поверхностная неструктурированная расчетная сетка с треугольными ячейками, пример которой приведен на рисунке 3. Физические параметры привязаны к центрам ячеек.

( а ) сетка на обледенелой поверхности

,            (б) фрагмент поверхности сетки аэродинамического профиля с контрольным объемом над одной из треугольных расчетных ячеек

Рисунок 3. Пример поверхностной неструктурированной расчетной сетки

На рисунке 3а приведен пример сетки, построенной на обледенелой поверхности аэродинамического профиля. В областях поверхности профиля, где присутствует ледяной нарост, сетка строится на поверхности льда, а в областях, где лед отсутствует — на поверхности аэродинамического профиля. На рисунке 3б детально показан фрагмент сетки с контрольным объемом над одной из треугольных расчетных ячеек. Общее количество ячеек 27 926.

Каждая итерация вычислений состоит из двух основных фаз: расчет протекания потоков массы и тепла между смежными ячейками через ребра расчетной сетки (моделирование течения пленки по поверхности) и определение состояния ячеек сетки (вычисление физических величин внутри ячеек). Для расчета течения жидкой пленки по поверхности используется конечно-объемный метод с противопотоковой схемой Роу первого порядка [16, 17]. Для определения состояния ячейки на каждой итерации расчетов система, составленная из уравнений массового и теплового балансов, решается относительно толщины слоя льда hice (м) и переменных T , hw . Толщина слоя льда hice связана с массовой скоростью замерзающей воды mice через дискретизацию по времени mice = Pice^hice^ hice'i-1), где hice,i — толщина слоя льда на текущей итерации расчетов, hice,i-1 — толщина слоя льда на предыдущей итерации расчетов, At —шаг по времени. В зависимости от фазового состояния льда/воды в ячейке эту систему уравнений можно замкнуть, уменьшив количество переменных до двух [18].

Состояни я льда/ в оды определяются в зависимости от значения температуры T . Если T = 0 ^о С, то рассматривается состояние глазурного льда («glaze ice»), при котором на поверхности может одновременно присутствовать и лед, и вода. В этом случае задача сводится к решению с истемы их двух линейных уравнений относительно h w и h ice . Если T <  0 ^о С, то рассматривается состояние изморози («rime ice»), при котором пленка воды отсутствует, то есть h w = 0. Если T >  0 ^о С, то рассматривается состояние жидкой пленки («wet surface»), при котором отсутствует слой льда, то есть h ice = 0. Если в ячейке отсутствует и лед, и вода, то рассматривается состояние сухой поверхности («dry surface»). Для состояний «rime ice», «wet surface», «dry surface» систем а уравнений сводится к одному нелинейному уравнению относительно T . Состояние ячейки считается определенным корректно, если выполнены все условия совместности:

h w >  0

m ice >  0

h w T >  0

_tm _ice T <  0

Если при определении физических величин для какого-либо состояния хотя бы одно из условий совместности нарушается, то предпринимается попытка найти решение с использованием другого состояния, как это показано на рисунке 4 . Например, при неудачном решении для состояния «glaze ice» сначала предпринимается попытка поиска решения для состояния «rime ice», а затем для состояния «wet surface». Если решение не может быть найдено ни для какого состояния, то фиксируется аварийная ситуация.

Наиболее затратной по времени процедурой в процессе расчетов ПМ Кристалл является решение нелинейного уравнения с одной переменной. В процессе проведения расчетов формула этого уравнения не может быть записана явно, а некоторые члены уравнения не являются дифференцируемыми. Поэтому для решения использовался комбинированный метод, все условия совместности выполнены

хотя бы одно из условий совместности не выполнено

проверка состояния

«dry surface»

т — hw ^ 0 V hice / 0

I

h w = 0 A h ice = 0

выбор состояния по текущей температуре r ---

T <  0             T = 0         T >  0

пересчет состояния «rime ice»

пересчет состояния «glaze ice»

пересчет состояния «glaze ice»

пересчет состояния «rime ice»

пересчет состояния «wet surface»

пересчет состояния «wet surface»

ERROR

пересчет состояния «dry surface»

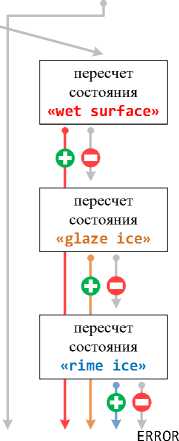
Рисунок 4. Последовательность поиска решения для разных состояний ячейки.

основанный на методе хорд с использованием отдельных итераций метода бисекций для избежания замедления сходимости или зацикливания [19] .

Для ускорения вычислений используется двухуровневое распараллеливание MPI+OpenMP. При распараллеливании вычислений по MPI декомпозиция расчетной сетки выполняется с помощью алгоритма Фархата, либо с помощью алгоритма пузырькового роста, начиная со случайных опорных ячеек [20]. Для улучшения масштабируемости используется механизм сокрытия издержек на межпроцессные обмены за основными вычислениями. Для этого ячейки каждого домена разбиваются на два подмножества: граничные ячейки — граничащие с границей домена, и внутренние ячейки — все остальные ячейки. На каждой итерации расчетов сначала обрабатываются граничные ячейки всех доменов, а затем межпроцессные обмены запускаются одновременно с обработкой внутренних ячеек доменов, как это показано на рисунке 5.

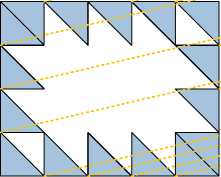
обработка граничных ячеек

обработка внутренних ячеек одновременно с межпроцессными обменами

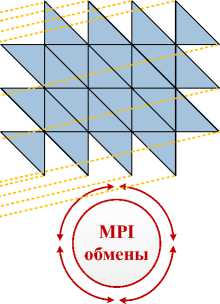
Рисунок 5. Организация межпроцессных обменов между доменами расчетной сетки.

При проведении одной итерации расчетов производится два основных цикла вычислений: цикл по всем ребрам расчетной сетки для пересчета протекания массового и теплового потоков и цикл всем ячейкам сетки для определения их состояний. При обработке ребра расчетной ячейки выполняется изменение консервативных величин инцидентных ему ячеек. Для устранения конфликтов по данным, потенциально возникающих при параллельной обработке ребер, множество ребер разбивается на множества неконфликтующих ребер путем построения реберной раскраски дуального графа сетки [21] .

После расчета высоты ледяных наростов в каждой ячейке выполняется перестроение расчетной сетки с учетом накопленного льда. В ПМ Кристалл используется набор различных методов перестроения расчетной сетки [22] , в том числе методы перестроения с представлением объема льда в ячейке с помощью треугольных призм и усеченных пирамид, многоуровневое итерационное перестроение поверхности, перестроение с сохранением объема льда в ячейках [23] .

3.    Результаты расчетов формирования льда в условиях крупных переохлажденных капель

Выбор надежных экспериментальных данных, полученных в условиях SLD, представляет собой сложную задачу, поскольку само моделирование подобных капель в условиях стенда практически трудно достижимо. Моделирование условий SLD предполагает, что капли воды большого диаметра (вплоть до 500 — 2000 мкм) должны иметь высокую скорость и отрицательную температуру, соответствующую параметрам воздушного потока, оставаясь при этом в жидком переохлажденном состоянии.

Данное метастабильное состояние может нарушаться при любом механическом воздействии (выпадение на твердую стенку или воздействие несущего воздушного потока), при этом капля переходит в устойчивое термодинамическое состояние с выделением энергии фазового перехода. После этого процесс замерзания содержащейся в ней воды протекает по стандартным сценариям, то есть ее замерзание происходит при понижении температуры ниже 0 ^o C.

Для недопущения дробления капель и замерзания форсунок впрыскивание воды в поток должно происходить при умеренных скоростях воздуха и при положительной температуре воды. Однако для недопущения дробления капель и замерзания форсунок впрыскивание воды в поток должно происходить при умеренных скоростях воздуха и при положительной температуре воды. На стенде должны быть созданы условия, при которых дальнейшее охлаждение капель и ускорение воздушным потоком не должно приводить к дроблению и выпадению на стенки канала, при этом сопровождаться их переохлаждением до отрицательных температур, не допуская замерзания.

Совместное удовлетворение перечисленных условий на практике сталкивается с рядом физических противоречий, поэтому реальные стенды не по всем параметрам удовлетворяют требованиям, предъявляемым к моделированию реального атмосферного крупнокапельного облака SLD. Среди доступных результатов испытаний элементов авиационной техники в условиях SLD, экспериментальные данные [24] , полученные в процессе разработки европейского проекта Ice Genesis, заслуживают наибольшего доверия.

Корректность оценивается по критериям, характеризующим тип образующегося ледяного нароста («rime ice» или «glaze ice»), наличие и места локализации рогообразных и иных ледяных форм, толщин льда в характерных областях нароста. Анализ форм ледяных наростов

304 А.В. Горячев, П.А. Горячев, Д.А. Горячев, М.В. Нуриев, А.А. Николаев, А.A. Рыбаков согласно этим критериям позволяет оценить локализацию мест выпадения капель и интенсивность их разбрызгивания, растекание жидкой воды по поверхности и скорость ее замерзания.

Для верификации описания предложенной моделью наиболее значимых физических явлений, сопровождающих процесс льдообразования в условиях SLD, выбраны 7 экспериментальных режимов с общими параметрами испытаний

• ^•    продолжительность испытания 450 мс,

• ^•    угол атаки аэродинамического профиля относительно набегающего потока 2 градуса,

• ^•    барометрическая высота над уровнем моря, на которой выполнялись испытания объекта 0 м,

• ^•    массовое содержание воды в потоке воздуха LWC = 0.3 г/м ³

и варьируемыми в соответствии с таблицей 1 значениями среднего медианного диаметра капель MVD, статической температуры во внешнем потоке OAT и скорости потока воздуха U _∞ .

Таблица 1. Варьируемые условия моделирования обледенения в условиях крупных переохлажденных капель SLD.

№	MVD (мкм)	OAT ( О С)	U ^ (м/с)
1	104	-10	65
2	180	-25	158
3	040	-25	158
4	104	-10	163
5	040	-25	63
6	180	-25	63
7	104	-25	63

Расчет форм льда выполнялся программным комплексом ПМ Кристалл [4] с использованием предлагаемой модели. На рисунке 6 представлено сравнение результатов расчета по предлагаемой модели с ПК Ansys FensapIce и с экспериментальными данными [24] , выполненными в условиях крупных переохлажденных капель SLD.

В таблице 2 представлены результаты анализа соответствия расчетных и экспериментальных льдообразований указанным критериям.

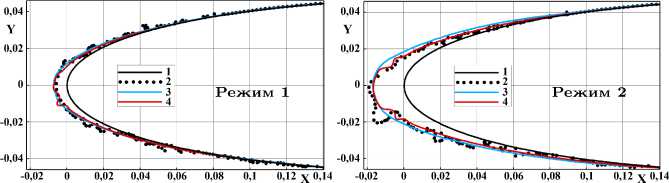
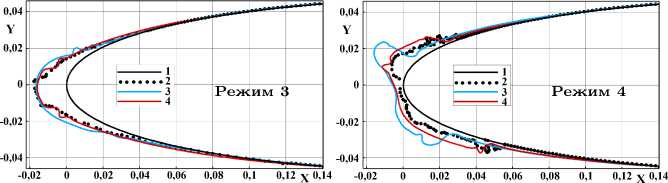
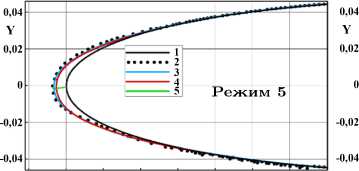
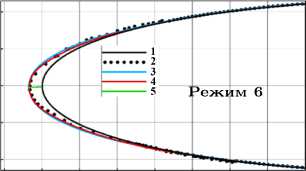
-0,02    0     0,02   0,04   0,06   0,08    0,1    0,12 X 0,14    -0,02    0     0,02   0,04   0,06   0,08    0,1   0,12 X 0,14

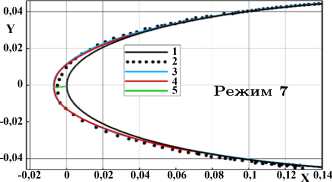
1 — профиль NACA 0012; форма льда, полученная: 2 — в эксперименте [24] , 3 — в расчете ПМ Fensap-Ice, 4 — в расчете по настоящей модели;

5 — сечение толщины льда в области передней критической точки; толщина льда на границах «рога» или трапециевидного нароста:

Рисунок 6. Формы льда в режимах таблицы 1

Таблица 2. Сравнение расчетных форм ледяных наростов с экспериментальными данными [24] (F — результаты расчета по ПК Ansys Fensap-Ice, К — результаты расчета по предлагаемой модели)

Критерии сравнения результатов расчетов с экспериментальными данными	Номер режима в таблице 1
	1		2		3		4		5		6		7
	F	K	F	K	F	K	F	K	F	K	F	K	F	K
Типа нароста «rime ice»	+	+	+	+	+	+	-	-	+	+	+	+	+	+
Тип нароста «glaze ice»	-	-	-	-	-	-	+	+	-	-	-	-	-	-
Наличие рогообразных наростов	-	-	-	-	-	-	+	+	-	-	-	-	-	-
Погрешность (мм)      верхн. в локализации «рога» на поверхности профиля нижн.							03, 4 11,7	04, 4 01,3
Погрешность (мм)      верхн. в локализации «рога» на поверхности профиля нижн.							03, 4 11,7	04, 4 01,3
Толщина льда в области верхн. «рогов» (мм)           нижн.							21,3 13,1	12, 9 07, 8
Наличие трапециевидных выступов в передней части нароста	-	-	-	+	-	+	-	-	-	-	-	-	-	-
Погрешность (мм)      верхн. в локализации границ трапециевидных выступов на поверхности нижн. профиля                    .			5, 7 1,9		3, 7 0, 7
Толщина льда (мм) в области трапециевидных выступов погрешность относительно экспериментальных данных				16, 8 -4,8		16, 0 -2,6
Толщина льда (мм) в передней критической точке погрешность относительно экспериментальных данных	007, 3 +1, 6	007, 3 +1, 6	016, 8 -2,4	016, 8 -2,4	170 -0,1	015, 9 -1,2	004, 9 +3, 3	004, 4 +2, 8	006, 3 -0, 7	004, 9 -2,1	6, 7 000	6, 7 000	6, 7 +2	006, 6 +1, 9

306 А.В. Горячев, П.А. Горячев, Д.А. Горячев, М.В. Нуриев, А.А. Николаев, А.A. Рыбаков

Из анализа данных, представленного в таблице 2 следует, что оба программных комплекса корректно предсказывают тип образующихся ледяных наростов. в режимах 1–3, 5–7 образуются наросты типа «rime ice», для которых характерно замерзание капель в месте их выпадения, а в режиме 3 реализуется растекание воды по поверхности льда, при этом формируются наросты типа «glaze ice».

В режимах 5–7, характеризующихся наиболее низкими температурами и скоростями потока, получены гладкие ледяные наросты типа «rime ice», по форме соответствующие экспериментальным данным (рисунка 6) . Полученные формы характерны для условий обледенения, при которых происходит полное замерзание выпадающих капель без растекания воды по поверхности льда. Расчетная толщина льда в области передней критической точки соответствует экспериментальным данным с погрешностью до 2,1 мм. Аналогичные результаты по формам и размерам ледяных наростов получены с использованием ПК Ansys Fensap-Ice.

В режимах 1–3, характеризующихся более высокими температурами и скоростями потока, получены формы льда хорошо соответствующие экспериментальным данным по границам областей обледенения и толщинам льда в лобовой части ледяного нароста на рисунке 6. В расчетах получена более гладкие формы льда по сравнению с экспериментом, в котором наблюдалось образование крупных ледяных сталактитов, направленных навстречу потоку. Подобные формы образуются в процессе течения жидкости по поверхности льда, ее частичного срыва во внешний поток в виде капель и вторичного выпадения этих капель на поверхность. Однако, подобные явления протекать не могут, поскольку на указанных режимах реализуются условия обледенения типа «rime ice», при этом величина температуры на поверхности льда ниже 0 ^о С и отсутствует течение жидкой воды.

Указанное несоответствие можно объяснить недостаточным переохлаждением крупных капель, получаемых при испытаниях, поскольку их генерация в условиях стенда является крайне сложной задачей. Недоохлажденные крупные капли при выпадении на поверхность льда могут растекаться в виде жидкой пленки, образуя поверхность с ледяными сталактитами, наблюдавшимися в испытаниях. В наибольшей степени данное явление наблюдается для наиболее крупных капель, которые труднее всего поддаются переохлаждению. Максимальное образование сталактитов наблюдалось в режимах 1 и 2 на рисунке 6 , для которых величина MVD составляла 104 и 180 мкм, соответственно. В режиме 3 величина MVD = 40 мкм и образование сталактитов на рисунке 6 существенно меньше.

Аналогично результатам, полученным с использованием предлагаемой модели в режимах 1–3, наросты льда, рассчитанные с использованием ПМ Ansys Fensap-Ice, являются гладкими, с отсутствием крупных сталактитов (рисунок 6) .

Для нароста типа «glaze ice» (режим 4) оба расчета предсказывают формирование рогообразных наростов, а для «rime ice» (режимы 1–4, 5–7) — их отсутствие (таблица 2) .

Наиболее сложным случаем моделирования представляется режим 4, на котором реализуются условия обледенения типа «glaze ice». При этом величина температуры на поверхности льда равна 0 ^о С, и присутствует течение жидкой воды, которая постепенно замерзает с образование характерных «рогов». При использовании предлагаемой модели погрешности в предсказании места локализации «рога» и его толщины составляют для верхнего и нижнего рога 4,4 мм и 1,3 мм. Для ПК Ansys Fensap-Ice эти величины составляют, соответственно, 3,4 мм и 11,7 мм. Из сравнения числовых характеристик расчетных и экспериментальных форм ледяных наростов следует, что предлагаемая модель позволяет достаточно точно рассчитать массогабаритные характеристики ледяного нароста типа «glaze ice» в условиях SLD.

Характерной особенностью процесса обледенения в условиях SLD является образование трапециевидных выступов в передней части нароста, полученных в режимах 2 и 3. Однако в расчетах ПК Ansys Fensap-Ice полностью отсутствует трапециевидный выступ в районе лобовой части ледяного нароста.

В результате расчета по предлагаемой модели в режиме 3 была получена форма ледяного нароста с характерным трапециевидным выступом в области передней критической точки. Образование подобной формы, вероятно, объясняется зависимостью величины разбрызгивания крупных капель от угла их падения на поверхность льда. Предложенная модель позволяет достаточно точно рассчитать подобную форму.

Аналогичное явление наблюдается и в режиме 2 на рисунке 6. В расчете, аналогично с режимом 3, получена форма трапециевидного выступа, однако в испытаниях передний выступ значительно опущен вниз с образованием «рога» в нижней части. Данное явление объясняется недостаточным переохлаждением крупных капель, вследствие которого часть жидкости под воздействием воздушного потока и силы тяжести стекает вниз. При этом весь трапециевидный выступ, образующийся в расчете при полном замерзании капель, в эксперименте как бы стекает вниз.

Для образования трапециевидного выступа необходимо достаточное количество воды, которое обеспечивается на режимах 2 и 3 высокой скоростью потока (158 м/с) (рисунок 6) . В режиме 1 на рисунке 6 подобный выступ не успевает сформироваться вследствие недостаточного количества воды, поступающей из потока со скоростью 65 м/с.

Предлагаемая модель позволяет достаточно точно предсказать образование трапециевидных выступов в передней части ледяного нароста, их локализацию (погрешность от 0,7 до 1,9 мм) и толщину (погрешность от -4,8 до -2,6 мм). ПК Ansys Fensap-Ice не позволяет рассчитать появление данных ледяных образований (таблица 2) . В расчетах получены гладкие ледяные формы, характерные для наростов типа «rime ice», образующихся в условиях мелкодисперсного атмосферного облака жидких переохлажденных капель.

Сравнение толщин льда, полученных в области передней критической точки, представлены в последней строке таблицы 2. В режимах 1– 3, 5–7 расчеты, выполненные обоими программными комплексами, хорошо соответствуют экспериментальным данным. Отличие в толщинах составляет от -2,4 до 1,9 мм. В режиме 4 (нарост типа «glaze ice») расчетные толщины отличаются от экспериментальных на величины от 2,8 до 3,3 мм.

Проведенное сравнение результатов расчета форм льда в условиях SLD с использованием предложенной модели с результатами ПК Ansys Fensap-Ice позволяет выявить следующее. При моделировании наиболее гладких ледяных наростов типа «rime ice» (режимы 1, 5–7) оба расчета дают близкие результаты, корректно предсказывающие форму и толщину льда в области передней критической точки и в периферийных областях ледяного нароста. Предлагаемая модель позволяет значительно повысить точность расчета наиболее сложных ледяных форм типа «glaze ice» (режим 4 на рисунке 6) , снизить погрешность определения геометрических размеров «рогов» и мест их локализации на поверхности объекта.

Существенным преимуществом предлагаемой модели по сравнению с ПК Ansys Fensap-Ice является возможность расчета трапециевидных выступов в передней части ледяного нароста (режимы 2 и 3 на рисунке 6) , полученных в процессе испытаний. В отличие от рогообразных наростов типа «glaze ice», формирующихся в процессе течения жидкой воды по поверхности (режим 4 на рисунке 6 , на режимах 2 и 3 образуются трапециевидные выступы в передней части ледяного нароста типа «rime ice». При этом рост льда происходит в условиях полного замерзания выпадающих капель и отсутствия течения жидкости по поверхности. Формирование трапециевидных выступов происходит вследствие различия

310 А.В. Горячев, П.А. Горячев, Д.А. Горячев, М.В. Нуриев, А.А. Николаев, А.A. Рыбаков RU EN в разбрызгивании капель, выпадающих на различные участки поверхности льда. Предложенная модель позволяет корректно описать изменение распределения величины местного коэффициента потери массы по поверхности ледяного нароста, что подтверждается соответствием расчетов экспериментальным данным на рисунке 6. Таким образом, представленные результаты расчета имеют хорошее совпадение с экспериментальными данными и показывают преимущества применения модели в сравнении с другими современными программными комплексами. Предлагаемая модель позволяет выполнять расчет процесса обледенения элементов авиационной техники в широком диапазоне условий обледенения, включая условия жидких переохлажденных капель.

Заключение

Для описания нестационарного процесса формирования льда на поверхностях летательного аппарата в атмосферных условиях крупных переохлажденных капель (SLD) предложен метод, позволяющий повысить точность расчета форм, локализации ледяных наростов и температурного состояния обледеневающей поверхности.

Формирование ледяного нароста, описывается с использованием следующих математических моделей: течения жидких пленок на поверхности льда SWIM, а также модели осаждения и разбрызгивания крупных капель при ударе о поверхность льда. Предложено усовершенствование модели, позволяющее рассчитать процесс разбрызгивания как для сухих, так и для влажных поверхностей. Валидация предложенного метода выполнена путем сравнения результатов расчетов с имеющимися экспериментальными данными, полученными на модельном профиле NACA0012 условиях SLD. В процессе валидации продемонстрирована возможность расчета сложных форм ледяных наростов, включая трапециевидные выступы в передней части ледяных наростов, характерные для условий SLD. Данные расчетов показали лучшее соответствие с экспериментом по форме, размерам и локализации образующихся ледяных наростов по сравнению с результатами, полученными с использованием программного комплекса Ansys Fensap-Ice.