Численное моделирование продольных колебаний в диспергирующих средах

Пусть Q ограниченная область в R n , n_ е N с границей dQ класса С ” . В цилиндре Qx R + рассмотрим уравнение Буссинеска - Лява

(Я - А)и = б/(А - Я^и + /?(А - Я> + f( (и)(1)

с краевыми условиями и (x, t ) = 0, (x, t )е SQxR(2)

и условиями Коши и (x ,0) = и 0( x), и (x ,0) = u1( x)

или условиями Шоуолтера - Сидорова

(Я-А)( и ( x ,0) и ₀( x )) = 0, (Я-А)( и ( x ,0) u 1 ( x )) = 0,(4)

где а, в, X, X, X е R , /(и) - функция класса С”, и(x,t) - искомая функция, она может иметь различный физический смысл в зависимости от задачи. Уравнение (1) является более общим слу чаем уравнения д 2р    д2р        д3р        д4р

- c0    = mcpc     - mc0 —-—-, д t2     x х2         5 t2 Bx       d t2 6x 2

где p - плотность, c0 - скорость звука, т - время релаксации, первый член в правой части отвечает за затухание звуковой волны вследствие теплопроводности и вязкости, а второй регулирует дисперсионные эффекты [5]. Уравнение (5) описывает распространение гравитационно -гироскопических волн в диспергирующих средах, например поверхностно-акустические волны. Обозначим через о (А) = {Xk} множество собственных значений однородной задачи Дирихле для оператора Лапласа в области Q. При X, не принадлежащем о (А), задача (1), (2), (3) хорошо исследована и доказаны теоремы о существовании единственного решения, например [4]. В противном случае задача (1), (2), (3) является принципиально неразрешимой при произвольных начальных значениях и0(x), и1 (x), она была исследована в [6] с помощью метода фазового пространства. Задача (1), (2), (4) сводится в подходящим образом выбранных банаховых пространствах к задаче Шоуолтера - Сидорова

P(и(0) и0) = 0, P(и(0) и1) = 0,(6)

где p - некоторый спектральный проектор, а задача (1), (2), (3) - к задаче Коши и (0) = и 0, и (0) = и1

для уравнения соболевского типа

Аи = В1и4-В0 и + N (и).

Стоит заметить, что задача Шоуолтера - Си дорова является частным случаем начальноконечной задачи [1], [3]. Целью работы является исследование существования решения и численное решение задачи (1), (3), (4) при произвольных начальных значениях и0(x), и1 (x), а также численное исследование задачи (1), (2), (4), при Я, не принадлежащем о(А), методом Галеркина.

ЗАДАЧА ШОУОЛТЕРА – СИДОРОВА ДЛЯ УРАВНЕНИЯ БУССИНЕСКА – ЛЯВА

Задачу (1), (2), (4) сведем к абстрактной задаче (6), (8), для этого зададим пространства

U = { u ( x ) е W₂^M (Q) | u ( x,t )=0, u ( x,t ) е dQxR}

F = W 2 (Q).

Тогда операторы A, B1, B0 имеют следующий вид: A = (X - А), B1 = а(А - X), B0 = в(А - X1) и принадлежат пространству L(U,F) (линейных и ограниченных операторов). Оператор, определенный формулой N(и) = А/и) при l > n/2 - 2, принадлежит классу С” [4]. Обозначим через {ф^ множество соответствующих им собственных функций, ортонормированных в смысле скалярного произведения пространства L2(Q). Построим проектор P(•) = I - ^ < •, фк >фк, действую- k щий в пространстве U, и проектор Q, имеющий тот же вид, но определенный в пространстве F. Обозначим через U и F0 соответственно ker P

и ker Q . Тогда условия Шоуолтера – Сидорова (4) можно переписать в виде

I-^u (0)- u 0 , Фк >Фк =0, I-^<^{U (0})- u 1 , Фk >Фк =0 . kk

Редукция задачи (1), (2), (4) к задаче (6), (8) окончена.

В [2] доказано, что если λ не принадлежит σ(∆) или λ = λ '≠ λ'' , тогда пучок операторов B₁ и B₀ является полиномиально А -ограниченным, ∞ является устранимой особой точкой и выполнены все условия теоремы о существовании единственного локального решения абстрактной задачи (7), (8) [6].

Заметим, что в случае задачи Шоуолтера – Сидорова начальные условия задаются как проекции на образ оператора при старшей производной, который в случае, когда ∞ – устранимая особая точка А -резольвенты пучка B , совпадает с образом проектора P . Таким образом, начальные значения задачи Шоуолтера – Сидорова автоматически попадают в фазовое пространство заданного уравнения, в отличие от начальных значений в задаче Коши.

Следовательно, для задачи (1), (2), (4) справедлива

Теорема 1. Пусть l > n/2 – 2 , λ = λ' ≠ λ'' или λ не принадлежит σ (∆) и отображение (I – Q)(B 0 + N u ₀ ):U⁰→F⁰ является топлинейным изоморфизмом. Тогда для любых u₀, u₁ ∈ U существует единственное решение задачи (1), (2), (4) (задачи (1), (2), (3)).

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ КОЛЕБАНИЙ В ДИСПЕРГИРУЮЩИХ СРЕДАХ

На основе теоретических результатов был разработан и реализован алгоритм численного решения задачи Шоуолтера – Сидорова для уравнения Буссинеска – Лява (1) в среде Maple 15.0. Разработанная программа позволяет:

• 1.    Ввести коэффициенты α , β , λ , λ' , λ'' , функцию f ( u ), начальные данные u₀ ( x ) , u₁ ( x ) и длину отрезка.

• 2.    Вывести приближенное решение задачи Шоуолтера – Сидорова (Коши) для уравнения (1) с условиями Дирихле.

• 3.    Получить графическое изображение полученного приближенного решения.

• 4.    Построить фазовое пространство уравнения (1).

Решение задачи (1), (2), (4) будем искать в виде галеркинской суммы

u ( x , t ) ³ u k ( t ) k ( x ),                    (9)

n 1

где φ_k ( x ) – собственные функции оператора Лапласа.

Пример 1. Требуется найти численное решение задачи (1), (2), (3) при λ = λ' = λ'' = 0, α = β = 1, f ( u ) = u³, u ( 0,t ) = u ( π,t ) = 0, u₀ = sin( x ) - sin( 2x ) + 3 sin( 3x ), u₁ = 5 sin( x ) на отрезке [0, π ].

Решение. В полосе [0, π ]× R₊ рассмотрим задачу

u (0, t ) u ( , t ) 0,                    (10)

u ( x ,0) = sin( x ) - sin(2 x ) + 3sin(3 x ) , u(x ,0) = 5sin( x ) ,(11)

-A u = A u + A u + A( u ³).

Собственные функции φ_k однородной задачи

Дирихле для оператора Лапласа на отрезке [0, π ]

Г2

имеют вид J — sin(kx). Очевидно, уравнение (12) п является невырожденным. В этом случае фазовым пространством является пространство U. В силу (9) решение имеет вид

u

( u 1 ( t ) sin( x ) + u ₂ ( t ) sin(2 x ) + u ₃ ( t ) sin(3 x )) .

Подставив ũ ( x,t ) в уравнение (12) и умножив ска-лярно в смысле L₂([0, π ]) полученное равенство на функции φ_k , k = 1, 2, 3, получим систему нелинейных дифференциальных уравнений (13) для нахождения u_k ( t ).

5,01326 f - d^ u 2 ( t )

- 5,01326 ^f du ₂( t )p 5,01326 u ₂( t ) - 4,78732 u ₁( t ) u ₂( t ) u ₃( t ) -

- 4,78732 u ₂( t ) ( u ₃( t ) ) ² - 4,78732 ( u ₁( t ) ) ² u ₂( t ) - 2,39366 ( u ₂( t ) ) 3 ,

1, 25331 ^f d 2 u ₁( t ) ^ = - 1,25331 ^f d, u ₁( t )p 0,598414 ( u ₁( t ) ) ² u 3 ( t ) - 0,598414 u ₃( t ) -

- 1,25331 u ₁( t ) - 1,19683 u ₁( t ) ( u ₃( t ) ) 2 - 0,598414 ( u ₂( t ) ) 2 u ₃( t ) - 1,19683 u ₁( t ) ( u ₂( t ) ) 2

1 1,2798 ^f d ^ u 3 ( t ) j = - 1 1,2798 ^f du 3 ( t )p 1,79524 ( u 1 ( t ) ) ³ - 10,7715 u 3 ( t ) ( u 1 ( t ) ) ² -- 10,7715 ( u 2 ( t ) ) ² u 3 ( t ) - 5,38573 u 1 ( t ) ( u 2 ( t ) ) 2 - 1 1,2798 u 3 ( t ) - 5,38573( u 3 ( t )) 3 .

На рис. 1 изображен график приближенного решения задачи (10)–(12) с шагами ∆x = 0,003 и ∆ t = 0,2.

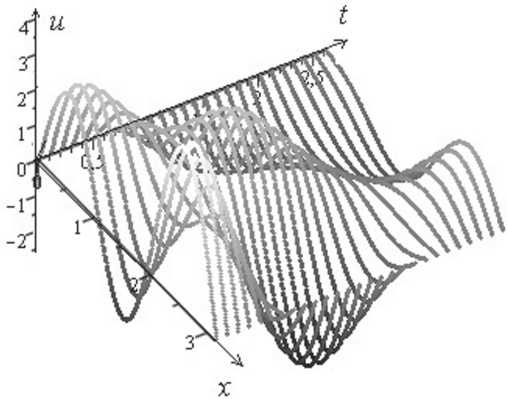
Рис. 1. График приближенного решения задачи (10)–(12)

Пример 2. Требуется найти численное решение задачи (1), (2), (4) при λ = λ' = -9, λ'' = 0, α = β = 1 , f ( u ) = u³ , u ( 0,t ) = u ( π,t ) = 0 , u₀ = sin( x ) - sin( 2x ) + 3 sin( 3x ), u₁ = 5 sin( x ) на отрезке [0, π ]. Решение. Задача (1), (2), (4) примет вид

(-9 -A) u = (A + 9) u + A u + A( u ³),       (14)

u (0, t ) = u ( n , t ) = 0,                (15)

( -9-A ) ( u ( x ,0 ) -sin x + sin2 x -3sin3 x ) = 0, ( -9-A ) ( u ( x ,0 ) -5sin x ) = 0 . (16)

Уравнение (14) является вырожденным. В силу (9) решение имеет вид

U(x X , t )

= J—( u 1 ( t ) sin( x ) + u ₂ ( t ) sin(2 x ) + u ₃ ( t ) sin(3 x )) X n

Проделав те же процедуры, что и в примере 1, получим алгебро-дифференциальную систему уравнений (17).

Алгебраическое уравнение определяет фазовое пространство уравнения (14). Решив систему из двух дифференциальных уравнений, подставив результат в алгебраическое уравнение, получим решение задачи (14)–(16).

- 10,0265 ^u, ( t ) = 10,0265 1 —u .( t ) 1 + 0,598414( u .( t ))² u ₃( t ) - 0,598414( u ,( t ))² u ₃( t ) I dt ²                       dt

- 1,19683 u 1 ( t )( u ₂ ( t ))² - 1,19683 u 1 ( t )( u ₃ ( t ))² - 2,50663 u 1 ( t ) - 0,598414( u 1 ( t ))³,

- 6,26657

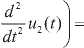
- 6,26657 1 ^—u ₂( t ) I - 6,26657 u ₂ ( t ) - 4,78732 u ₂ ( t )( u ₃( t ))² - (17) V dt )

- 4,78732( u 1 ( t ))² u ₂ ( t ) - 4,78732 u 1 ( t ) u ₂ ( t ) u ₃ ( t ) - 2,39366 ( u ₂ ( t ) ) ³,

0 = 10,7715 u 1 ( t )( u ₂ ( t ))² + 10,7715( u ₂ ( t ))² u ₃ ( t ) - 1,79524( u ₃ ( t ))³ + 12,5313 u ₃ ( t ) + + 5,38573( u ₃( t ))³ + 5,38573 u 1 ( t )( u ₂( t ))².

В таблице приведено численное решение алгебро-дифференциальной системы при начальных условиях u, (0) = ^2 , u2 (0) = -^|, zi, (0) = 5^, «2(0) = 0 .

Приближенное решение системы (17)

t	u 1( t )	u 2( t )	u 3( t )
0	1,253	-1,253	-0,152
0,1	1,853	-1,272	-0,070
0,2	2,408	-1,340	0,018
0,3	2,929	-1,482	0,081
0,4	3,429	-1,734	0,098
0,5	3,925	-2,154	0,045
0,6	4,439	-2,845	0,116
0,7	5,010	-3,998	-0,450
0,8	5,713	-6,042	-1,032
0,9	6,744	-10,228	-1,968
1,0	8,8407	-23,046	-3,618

На рис. 2 изображено фазовое пространство (16). На рис. 3 построено поточечно численное решение примера 2 с шагами ∆x = 0,002 и ∆ t = 0,1

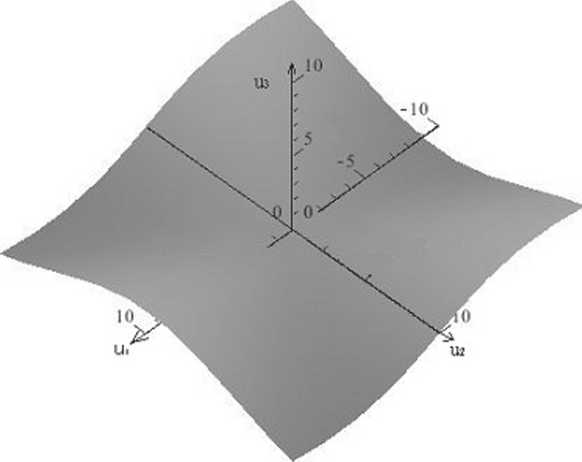
Рис. 2. Фазовое пространство уравнения (16)

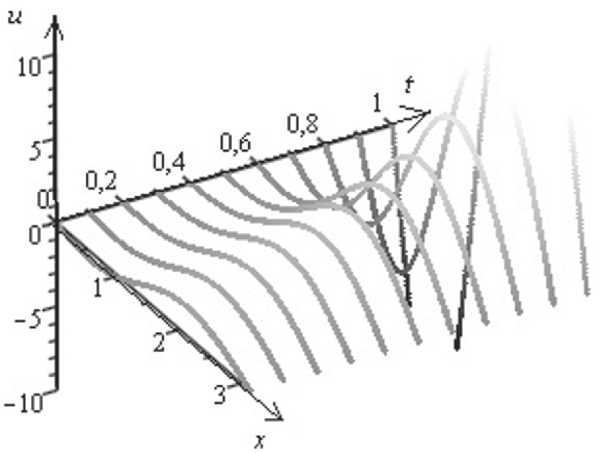
Рис. 3. График приближенного решения задачи (16)–(18)

БЛАГОДАРНОСТЬ

Выражаю благодарность Георгию Анатольевичу Свиридюку за поддержку и ценные советы.