Численное моделирование пространственных волновых движений в моментных средах

возможность существенно измельчать расчетные сетки, тем самым повышая точность решения.

Вопросы численного решения динамических задач в рамках моментной теории упругости рассматриваются в работах [1, 2]. В настоящей работе приводятся результаты анализа колебательных процессов, показывающие, что в моментных средах существует характерная резонансная частота, соответствующая частоте собственных колебаний вращательного движения частиц, которая связана только с инерционными свойствами частиц микроструктуры материала и не зависит от размеров исследуемой области и условий на ее границе.

1. Математическая модель

В модели моментной упругой среды, кроме поступательного движения, которое характеризуется вектором скорости v , рассматриваются независимые повороты частиц с вектором угловой скорости и , а наряду с тензором напряжений о , компоненты которого несимметричны, вводится несимметричный тензор моментных напряжений m . Полную систему уравнений модели образуют уравнения движения, кинематические соотношения и обобщенный закон линейной теории упругости [3, 4]:

р v = V•о + р g, j b = V- m - 2 о a + jq, Л = V v + и, Ml = Vto, ох (5: Л) 5 + 2 цЛ5 + 2 аЛ a, m = p (5: M) 5 + 2 у Ms + 2 a Ma.

Здесь р — плотность среды, j — суммарный момент инерции частиц в единице объема, g и q — векторы массовых сил и моментов, Л и M — тензоры деформаций и кривизн, X , ц , а , в , у и а — феноменологические коэффициенты упругости для изотропного материала, 5 — метрический тензор. Используются общепринятые обозначения и операции тензорного анализа: двоеточие означает двойную свертку, точка над символом — производную по времени, звездочка — транспонирование тензора. Верхними индексами 5 и a отмечены симметричная и антисимметричная составляющие тензоров. С антисимметричной составляющей, где это необходимо, отождествляется соответствующий ей вектор. В частности, в уравнения вращательного движения входит вектор тензора о a = ( о - о * ) / 2 .

Для оценки линейного параметра микроструктуры материала справедлива формула r = V5 j /(2 р ), основанная на модельном представлении о среде как о плотной упаковке ансамбля шарообразных частиц одинакового радиуса.

Для пространственного случая система уравнений (1) в декартовой системе координат имеет следующий развернутый вид:

Р v = о1 i,1 +о2i,2 +озi,3 +Р gi , a1 оп+ a2 (оkk +оll) = vi.i, a 3 о ik + a 4 о ki = vk, i -b l , a4 ^k + a3 о ki = vi, k + bl ,

^{j b} = m b-, 1 ^{+ m} 2 i , 2 ^{+ m} 3 i, 3 ^+о kl - ^о lk ^{+ j} q i , bl m ii + b 2 ⁽ m kk ⁺ m ll ) = ^b i , i , ^b 3 rh _a ⁺ b 4 rm ki =^b k , i ,

b 4 rh_a + ^b 3 rm _м = ^ь -, k .

Система (2) включает 24 уравнения относительно 24-х неизвестных функций. Нижние индексы после запятой служат для обозначения частных производных по соответствующим пространственным координатам. Также используются обозначения:

i , k , l = 1, 2, 3, i * k * l , k = i + 1 mod 3, l = k + 1 mod 3,

Х + ц             X          ц + а a-ц a1 =-------------, a 2 =--, a 3 =------, a 4 =------,(3)

ц (3 X + 2 ц)         2 ц (3 X + 2 ц)       4 ца 4 ца bi=P+^, b2 =₽, b3 = !+s, b4 =£zl. Y (3 в + 2 у)          2 y (3 в + 2 y)         4 Y£

Систему уравнений (2) можно переписать в матричном виде [1]:

AU = B1 U,1 + B2 U,2 + B3 U,3 + QU + G,(4)

где U — вектор-функция, составленная из компонент векторов скорости и угловой скорости, несимметричных тензоров напряжений и моментных напряжений

^U = ^{( v} 1 , v 2 , v 3 , ⁰ц, ° ₂₂, 0 33 , ^3 , ^ ⁰_М, ⁰_n, ° ₁₂, ⁰ ₂₁, rn 1 , w ₂, w ₃, m 11 , m ₂₂, m ₃₃, m ₂₃, m ₃₂, m ₃₁, m ₁₃, m ₁₂, m ₂₁).

Матрицы-коэффициенты A , B ¹ , B ² и B ³ симметричны, а Q антисимметрична, G — заданный вектор массовых сил и моментов. Матрица A положительно определена, если положительно определенными являются ее диагональные блоки:

f ^a 1    ^a 2 ^a 2 )

a ₂    a 1    a ₂

V ^a 2    ^a 2 ^a 1 7

f a 3 a 4 л v a 4 a 3 7

f b b ²

V ^2

b ² b ²'

b  b 2

b b и2 ux 7

bb ь3 7

V b 4 ^b3 7

Это условие ограничивает допустимые значения параметров среды:

3 X + 2 ц , ц , a > 0,     3 в + 2 y , Y , ^£ > 0.                                                 (7)

При выполнении неравенств (7) потенциальная энергия упругой деформации представляет собой положительную квадратичную форму, а система (4) является гиперболической по Фридрихсу [5]. Ее характеристические свойства описываются уравнением

det( c A + n1 B1 + n 2 B2 + n 3 B3) = 0,     n2 + n 22 + n 33 = 1, положительные корни которого — скорости продольных волн cp , поперечных волн cs , волн кручения cm и волн вращательного движения cm, равны cp

Х + 2ц _ /ц + а , c s = Л

Р

Р

С

m

в + 2 Y

j

Y + s

j

Полную систему левых собственных векторов образуют 12 векторов, соответствующих ненулевым собственным числам ± c p , ± c s , ± c_m и ± c _m , среди которых ± c s и ± c _m являются двукратными, и 12 векторов для c = 0.

Для гиперболической системы (4) корректно поставлена краевая задача с начальными данными U(x, 0) = U0 (x) и диссипативными граничными условиями, выполнение которых для любых двух вектор-функций U и U обеспечивает выполнение в точках границы неравенства

( U - U )( n 1 B ¹ + n 2 B ² + n ₃ B ³)( U - U ) <  0.

В развернутой форме это неравенство выглядит так (по повторяющимся индексам k , I = 1, 2, 3 производится суммирование):

⁽ v i ^- V )( 6 _и - о _и ) n + ( to / ^- to / ⁾⁽ m_kl ^- т_ы ) n <  0.

К диссипативным, в частности, относятся граничные условия в скоростях и в напряжениях, которые в рамках модели моментной среды формулируются следующим образом:

v = v , _ю = ю , ° ki n k = p i , m ki n k = q . ⁽¹²⁾

Здесь p и q — заданные на границе векторы внешних усилий и моментов. Если на границе области не выполняются условия согласования между граничными и начальными значениями заданных функций или если эти функции разрывны, то образуются разрывы решения — ударные волны, для определения которых служит система уравнений сильного разрыва

( cA + n 1 B ¹ + n ₂ B ² + n ₃ B ³)[ U ] = 0, (13)

где [ U ] — скачок решения при переходе через фронт разрыва, c — скорость движения фронта в направлении вектора нормали n . Судя по этой системе, ударные волны малой амплитуды в моментной среде могут распространяться только со скоростями (9), и на фронтах волн скалярные произведения левых собственных векторов на вектор U остаются непрерывными.

При численном исследовании задач важную роль играют искусственные граничные условия, которые связаны с симметрией напряженно-деформированного состояния и позволяют многократно уменьшить объем вычислений. Эти условия следуют из инвариантности системы уравнений относительно простых преобразований, переводящих искусственные границы (например, плоскости симметрии) в себя. Заметим, что вектор угловой скорости to по существу является тензором второго ранга, а тензор моментов m — тензором третьего ранга. Формулы понижения ранга для них имеют вид:

to1   to32 ,     to2   toi3 ,     to3   to2i ,     mii   mi32 , m22   m213 , m33   m32i , m23 = m221,  m32 = m313,  m31 = m332 ,  m13 = m121 ,  m12 = m113 ,  m21 = m232 .

Следовательно при преобразовании, например, зеркального отражения x ₂ ^ - x ₂

меняются знаки величин to 1 , to ₃, m 11 , m ₂₂, m ₃₃, m ₃₁ и m ₁₃, в тензорных компонентах которых индекс 2 встречается только один раз. Эти величины на плоскости x ₂ = 0

оказываются равными нулю.

С целью решения пространственных задач об упругих волнах, вызванных действием сосредоточенного импульсного источника, в [2] приводятся граничные условия симметрии для различных типов нагружения. Если на поверхности полупространства х1 > 0 действует нормальная нагрузка оп =-p1 8(x) 5(t), сосредоточенная в начале координат, то плоскости x2 = 0 и x3 = 0 являются плоскостями симметрии. Система уравнений (2) инвариантна при зеркальном отражении x ^-x2, что на плоскости x2 = 0 обозначает равенство нулю компонент тензоров, меняющих свой знак:

v 2 = 0,   о ₂₁ о _-; = 0,   0) 1 0 3 = 0,   m ₂₂ = 0.                                            (15)

Плоскость x3 = 0 переходит в себя при зеркальном отражении x3 ^ -x3, поэтому на ней v3 = 0,  о31 = о32 = 0,  о1 =02 = 0,  m 33 = 0.                                       (16)

Если в точке x = 0 действует сосредоточенная касательная нагрузка ог = -p2 5(x) 5(t), то плоскость x3 = 0 является плоскостью симметрии, а x2 = 0 — плоскостью антисимметрии. Преобразование x2 ^ - x2, при котором плоскость x2 = 0 переходит в себя, меняет знак решения на противоположный: U ^ - U . Следовательно, на этой плоскости v1 = v3 = 0, о22 = 0, ю2 = 0, m 21 = m 23 = 0.                                          (17)

На плоскости x 3 = 0 выполняются условия (16).

При действии сосредоточенного момента m11 = - qx 5(x) 5(t), закручивающего частицу вокруг оси x1, оба зеркальных отражения x2 ^ -x2 и x3 ^ -x3 меняют знак решения: U ^ -U . Поэтому на плоскости антисимметрии x2 = 0 выполняются условия (17), а на плоскости x3 = 0 — аналогичные условия v1 = v2 = 0,  о33 = 0,  ю3 = 0,  m 31 = m32 = 0.

Если на границе действует сосредоточенный вращательный момент m ₁₂ = - q ₂ 5 ( x ) 5 ( t ), то преобразование зеркального отражения x ₃ ^ - x ₃ меняет знак решения, а x ₂ ^ - x ₂ — нет. Следовательно, на плоскости симметрии x ₂ = 0 выполняются условия (15), а на плоскости антисимметрии x ₃ = 0 — условия (18).

Можно показать, что граничные условия (15)–(18) являются диссипативными, поэтому их постановка обеспечивает корректность задачи.

Более общая математическая модель среды с микроструктурой, механические свойства которой меняются в зависимости от знака напряжений, учитывающая упругие связи между частицами и пластические деформации частиц, приводится к вариационному неравенству [1]

( Ё - V )( AI J - B ¹ V 1 - B ² V₂ - B ³ V 3 - QV - G ) > 0 ( V , V е F ) . (19)

Здесь вектор-функция V включает в себя компоненты векторов скорости и угловой скорости, тензоров напряжений и моментных напряжений, а в вектор-функцию U вместо истинных напряжений входят компоненты тензоров условных напряжений и условных моментных напряжений. Тензоры условных напряжений вычисляются по линейному закону Гука из системы уравнений (1). Вектор-функции V и U связаны между собой уравнениями

V = ^ U + (1 -^ ) U ^п ,

U = - V --2 V .

^      2

Здесь ξ — отношение модулей упругой податливости при растя жении и сжатии, U ^π — проекция U на конус K по евклидовой норме | U | _A = UAU , K — выпуклый конус напряжений, допускаемых критерием прочности, F — выпуклое и замкнутое множество, заданное критерием пластичности.

• 2.    Плоские волны

В одномерном случае, когда искомые функции зависят только от времени и одной из пространственных переменных, например, от x ₁ , система уравнений (2) распадается на четыре независимые подсистемы, описывающие: плоские продольные волны

Р ^v 1 = ^dm , ^d 11 = ⁽ ^ + ² Ц ) 4,1 , а 22 = ^d 33 = Х V ₁₄ ;

крутильные волны

• j ω ₁ = m _11,1 +σ ₂₃ -σ ₃₂, σ ₃₂ =-σ ₂₃ = 2 αω ₁, m ц = ( в + 2 y ) « 1,1 , m 22 = m 33 = в“ 1,1 ;

  
  

поперечные волны (волны сдвига) с вращением частиц р v2 = o121, d 12 = (ц + а) v21 - 2 ам,. d 21 = (ц-а) v21 + 2 аю3,

j (b ₃ = m₁₃₁ +d ₁₂ -d ₂₁, ^/m ₁₃ = ( Y + ⁸ ) ® ₃₁, ^m ₃₁ = ( Y — ^£ ) ^ю ₃₁.

Еще одна подсистема получается из (23) заменой индексов; она также описывает поперечные волны.

Общее решение подсистемы (21) выражается формулой Даламбера, в соответствии с которой продольные волны, как и в классической теории упругости, распространяются со скоростями ±cp и не обладают дисперсией. Подсистема крутильных волн (22) сводится к телеграфному уравнению относительно угловой скорости: b 1 = cmM111 - 4ам1 / j. Не зависящее от x1 решение телеграфного уравнения описывает равномерное колебательное вращение частиц среды с периодом колебаний T=π j/α. Анализ показывает, что на фронтах волн кручения возбуждается волнообразное вращательное движение частиц с характерной длиной волны, приблизительно равной произведению cm T. В работе [1] выполнен численный анализ уравнений поперечных волн (23) на основе конечноразностной схемы Неймана–Рихтмайера. Расчеты проводились для задачи об импульсном воздействии на упругую среду периодической системы Λ -образных импульсов касательного напряжения. Результаты показали, что при фиксированном времени угловая скорость, а также моментные напряжения представляют собой осциллирующие функции с характерной длиной волны cs T.

Согласно общей теории гиперболических систем, возмущения распространяются в рамках модели упругой среды с конечными скоростями (9). При этом возмущения, соответствующие поперечным волнам, автоматически порождают волны вращательного движения, и наоборот, возмущения вращательного движения приводят к поперечным волнам. На таких волнах, как и на крутильных, возникают осцилляции решения, что является основным качественным отличием модели моментной среды Коссера от классической линейной теории упругости. Другое отличие состоит в том, что в моментной среде имеется собственная частота акустического резонанса материала, не зависящая от размеров исследуемой области, которая проявляется при определенных условиях возмущения.

Действительно, в случае однородного напряженного состояния из системы (23) вытекает классическое резонансное уравнение j ё > 3 = - 4 а о ₃ + 2 а х , из которого следует, что если угол сдвига χ ( t ) изменяется по гармоническому закону с частотой ν _* = 1/ T , равной частоте собственных колебаний вращательного движения, то амплитуда угловой скорости частиц неограниченно растет. Данное уравнение описывает поведение бесконечного тонкого плоского упругого слоя, нижняя поверхность которого неподвижна, а верхняя движется по заданному закону.

В качестве примера рассматривался равномерный циклический сдвиг вязкоупругого слоя конечной толщины H . Как обычно, вязкость использовалась в качестве сглаживающего механизма. Процесс сдвига описывался уравнениями (23), в которых, в соответствии с теорией вязкоупругости Больцмана, произведения параметров среды на кинематические характеристики деформирования заменялись свертками соответствующих этим параметрам ядер релаксации на те же самые характеристики. Граничные условия задачи записывались в виде:

v | = v e ^{2 π i ν t} , ω | = 0, v | = 0, ω | = 0 (24)

2 x ₁ = 02 3 x ₁ = 0 2 x ₁ = H 3 x ₁ = H

(ось x ₁ направлена внутрь слоя). Система решалась спектральным методом: после применения преобразования Фурье из нее получалась система обыкновенных дифференциальных уравнений для амплитуд

4 π ² ν ² ρ v ₂ + ( µ + α ) v _2,11 - 2 αω _3,1 = 0,

4(π2ν2j-α)ω3 +(γ + ε) ω3,11 +2αv2,1 =0, решение которой строилось в явном виде с учетом граничных условий (24). Амплитуда касательного напряжения определялась через решение системы уравнений (25) по формуле: 2 п i v<3n = (ц + а) v2 1 - 2а со3. Для проверки достоверности результатов осуществлялось численное решение задачи на основе аппроксимирующей систему (25) спектрально-разностной схемы. Расчеты проводились методом матричной прогонки и на достаточно мелких сетках привели к практически неотличимым результатам. Расчетные феноменологические параметры среды подбирались по экспериментальным данным серии работ для тяжелой нефти в породе при достаточно низкой температуре, когда материал находится в твердой фазе (см. [6]).

На рисунке 1 приведены амплитудно-частотные зависимости для касательного напряжения на нижней поверхности вязкоупругого слоя. Рисунок 1, а относится к среде Коссера, на рисунке 1, б изображена такая же зависимость для обычной безмоментной вязкоупругой среды. Аналогичные графики для идеальных, невязких сред имеют систему резонансных пиков с бесконечными амплитудами.

Из сравнения графиков видно, что в моментной среде имеется дополнительная резонансная частота 23 кГц, близкая к частоте вращательного движения частиц, которая не зависит от толщины слоя. Это подтверждается большим количеством численных экспериментов для различных толщин. Как оказалось, изменение H приводит к смещению периодической системы основных резонансных частот, примерно равных νk=kcs/(2H) (k = 1, 2, ...), но при этом пик, соответствующий частоте ν*, остается неподвижным.

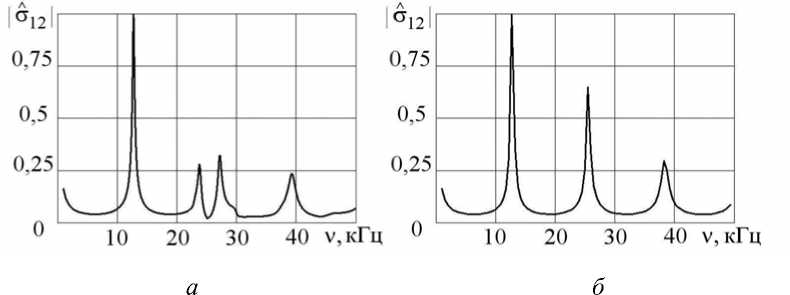
Рис. 1 . Характерные спектральные кривые касательного напряжения для континуума Коссера ( а ) и безмоментной вязкоупругой среды ( б )

Аналогичные расчеты для пенистого полиуретана не показали столь же заметного на фоне основных частот пика на резонансной частоте этого материала, имеющей тот же порядок, что и для тяжелой нефти. Это объясняется существенно более низкими моментными свойствами, выраженными в числовых значениях параметров j и α . Как оказалось, в материалах с низкими моментными свойствами резонанс вращательного движения частиц можно возбудить, например, за счет периодического изменения вращательного момента на границе слоя.

• 3.    Вычислительный алгоритм

• 4.    Результаты расчетов

Для модели моментного континуума Коссера и ее нелинейного обобщения на среды, по-разному сопротивляющиеся растяжению и сжатию, разработан параллельный алгоритм численной реализации на многопроцессорных суперкомпьютерах [1, 2]. Алгоритм решения линейной системы основан на методе двуциклического расщепления по пространственным переменным. Одномерные системы уравнений на этапах расщепления решаются с помощью явной монотонной ENO (Essentially NonOscillatory ) схемы типа «предиктор — корректор» с использованием кусочно-линейных сплайнов, разрывных на границах ячеек. Сплайны строятся на основе специальной процедуры предельной реконструкции [7], позволяющей повысить точность численного решения. Такая расчетная схема обладает свойством монотонности [8], поэтому она, в отличие от многих более простых схем, пригодна для исследования обобщенных решений в задачах об ударных, импульсных и сосредоточенных воздействиях.

Нелинейная система (19)–(20) реализуется с помощью метода расщепления по физическим процессам и приводит в каждой ячейке расчетной области к вариационному неравенству, описывающему пластическое деформирование материала с использованием специальных алгоритмов корректировки напряжений [1].

Создан комплекс параллельных программ для решения плоских и пространственных задач динамики моментной среды. Программирование выполнено на языке Fortran по технологии SPMD с использованием стандартной библиотеки передачи сообщений MPI. Универсальность программ достигается за счет специальной упаковки переменных каждого вычислительного узла кластера в одномерные массивы большой размерности. Распараллеливание вычислений осуществляется на этапе расщепления задачи по пространственным переменным. При решении одномерных систем уравнений обмен данными между вычислительными узлами происходит на шаге «предиктор» разностной схемы по обычной технологии законтурных ячеек. Каждый процессор сначала обменивается с соседними процессорами граничными значениями своих данных, а затем пересчитывает искомые величины в соответствии с разностной схемой. Расчетная область распределяется между узлами кластера по принципу равномерной загрузки.

Из соображений минимизации количества пересылок используются различные варианты разбиений — 1D, 2D или 3D. Для организации контрольных точек при счете каждый процессор формирует двоичные файлы прямого доступа, суммарный размер таких файлов на одном и том же шаге по времени может значительно превышать объем оперативной памяти отдельного процессора. Разработана процедура сжатия файлов, содержащих результаты вычислений, поскольку размер файлов может быть очень большим и для их транспортировки по сети потребуются значительные ресурсы. Графический вывод результатов осуществляется с помощью специальных программ, предназначенных для обычного персонального компьютера.

Тестирование алгоритма и комплекса программ выполнялось путем сопоставления результатов расчетов с точным решением двумерной задачи о распространении поверхностных волн Рэлея в среде Коссера [9], а также с точными решениями, описывающими одномерные движения среды с плоскими волнами. Расчеты собственных колебаний в моментной среде в двумерной постановке на основе разработанного алгоритма проведены в работе [1]. В статье [2] представлены результаты численного решения пространственной задачи Лэмба о мгновенном действии сосредоточенных сил и моментов на поверхности полупространства. На сейсмограммах, построенных по результатам расчетов в системе обработки геофизических данных SeisView, идентифицированы четыре типа волн — продольные, поперечные, крутильные и вращательные волны, распространяющиеся со скоростями (9). Расчеты пространственных задач подтвердили основное качественное отличие волнового поля в моментной среде Коссера от поля в классической теории упругости, которое заключается в появлении колебаний вращательного движения частиц на фронтах волн. Проведены сравнительные расчеты с различными значениями масштаба микроструктуры среды, в которых установлена прямая пропорциональная зависимость периода собственных колебаний от этого масштаба.

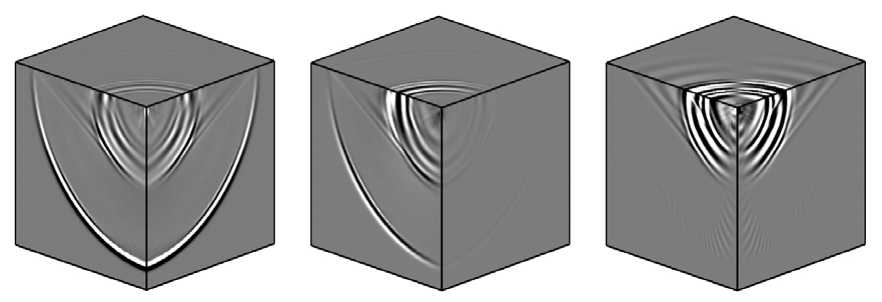
На рисунке 2 приведены поверхности уровня напряжений и момента в задаче Лэмба о действии сосредоточенной нормальной нагрузки σ ₁₁ =- p ₁ δ ( x ) δ ( t ) в угловой точке верхней границы расчетной области. Видны падающие продольные и поперечные волны, конические поперечные волны и поверхностные волны Рэлея. Расчетная область, с учетом условий симметрии, представляет собой четверть полупространства. В действительности расчеты проводились на кубе со стороной 1 см для синтетического полиуретана. Рисунки соответствуют моменту времени t = 3,3 мкс. Используемая

а                         б                          в

Рис. 2. Поверхности уровня напряжений σ11 (а), σ12 (б) и момента m23 (в) для задачи Лэмба в расчетах равномерная разностная сетка состояла из 200×200×200 ячеек. На более грубых сетках невозможно выполнить расчеты с приемлемой точностью, поскольку размер ячеек становится сравнимым с параметром микростуктуры среды. На искусственно введенных гранях куба ставились условия симметрии и неотражающие граничные условия, которые моделировали беспрепятственное прохождение волн. Расчеты выполнялись на 64-х узлах кластера, каждым из вычислительных узлов решалась часть задачи на подсетке размерностью 50×50×50 ячеек. Для расчета 200 шагов по времени потребовалось примерно 18 часов машинного времени.

На рисунке 3 изображены схема нагружения и сейсмограммы угла поворота частиц в плоскости x ₁ x ₂ вдоль трассы, проходящей через точку приложения нагрузки по оси x ₂ , для задачи Лэмба (Рис. 3, б ) и задачи о периодическом воздействии сосредоточенной нагрузки σ ₁₁ =- p ₁ δ ( x ) sin(2 πν t ) с частотой ν , равной собственной резонансной частоте ν_∗ (Рис. 3, в ). Сравнивая сейсмограммы по числу колебаний, можно заметить, что соответствующие длины волн практически совпадают.

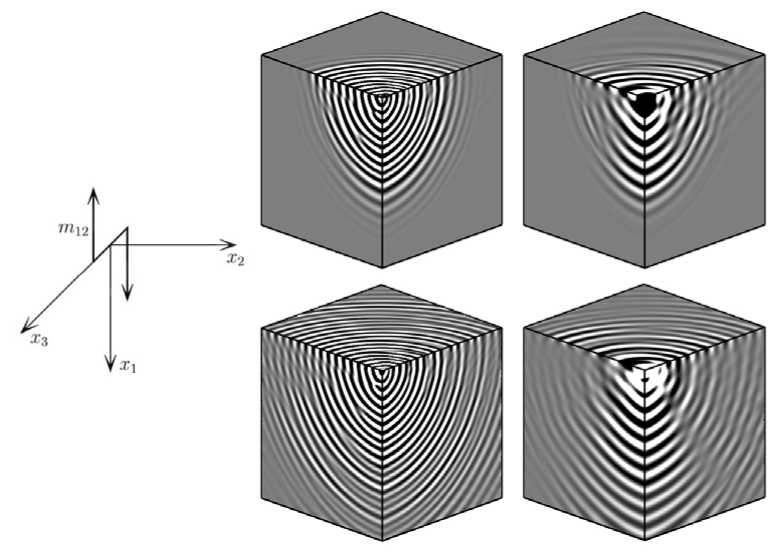
Далее представлены результаты решения задачи о действии сосредоточенного вращательного момента m ₁₂ =- q ₂ δ ( x ) sin(2 πν t ), изменяющегося периодически по времени. Рисунок 4 содержит схему нагружения, а также поверхности уровня угловой скорости ω ₂ для нерезонансной ( ν= 1,5 ν_∗ ) и резонансной ( ν =ν_∗ ) частот в различные моменты времени. Поверхности уровня соответствуют одному и тому же диапазону значений ω ₂ . Судя по рисунку, максимальная амплитуда колебаний угловой скорости достигается в точке приложения нагрузки, а длина волны существенно зависит от частоты. Сравнение показывает, что при частоте внешнего воздействия ν_∗ (Рис. 4, в ), равной собственной частоте вращательного движения частиц, происходит рост амплитуды со временем и более плавное затухание колебаний с удалением от точки приложения нагрузки, характерное для акустического резонанса.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 08-01-00148), Междисциплинарного интеграционного проекта Сибирского отделения РАН № 40 и Комплексной программы фундаментальных исследований Президиума РАН № 2 «Интеллектуальные информационные технологии, математическое моделирование, системный анализ и автоматизация».

а                            б                           в

Рис. 3. Схема нагружения ( а ) и сейсмограммы падающих волн в случае импульсного ( б ) и периодического ( в ) воздействий

а                        б                       в

Рис. 4 . Схема нагружения ( а ) и поверхности уровня угловой скорости м 2 для нерезонансной ( б) и резонансной ( в ) частот в различные моменты времени (вверху - t = 6,5 мкс, внизу - t = 13 мкс)