Численное моделирование распада топливной плёнки в низкоперепадной форсунке высокоресурсного авиационного двигателя

Интерес к исследуемой задаче обусловлен стоящей перед АО «ОДК–Авиадвигатель» необходимостью разработки подходов, позволяющих получать характеристики аэрозоля в керосиновых камерах сгорания с низкоперепадными форсунками. Эта проблема возникла в связи с переходом от высокоперепадных топливных форсунок, которые, в частности, использовались на двигателе ПС-90А [1], к низкоперепадным.

Распад плёнки в высокоперепадных центробежных форсунках определяется их геометрией и кинетической энергией, которую топливу сообщает насос. В силу того, что топливо является несжимаемой жидкостью, на основе экспериментальных данных можно построить зависимости характеристик форсунки от перепада давления, а не от его абсолютного значения. В низкоперепадных же форсунках большая часть энергии передаётся топливу от воздуха, плотность которого в камере сгорания в условиях крейсерского режима равна 13 кг/м3. Вследствие этого на экспериментальных установках, в которых давление на выходе из низкоперепадной форсунки в области распыла топлива нельзя повышать от атмосферного значения до 3 МПа, можно получать данные, которые дают только качественное представление о распыле топлива

в условиях работающего авиационного двигателя. Исследования, проведённые на подобных установках [2–6], позволили создать классификацию режимов распада топливной плёнки в низкоперепадной форсунке [5, 6]. Однако остается невыясненным вопрос, как эти результаты соотносятся с распылом топлива на крейсерском режиме, для изучения которого к настоящему моменту времени экспериментальные стенды ещё не созданы.

Альтернативой реальным экспериментам являются виртуальные, в которых для моделирования распыла топлива используется метод объёма жидкости. В высокоперепадных форсунках этот метод применялся для получения таких характеристик, как длина нераспавшейся плёнки [7], коэффициент расхода топлива [8, 9], угол раствора конуса распыла [8], профили и векторные поля течения в форсунке [9–11], скорости и диаметры капель [12]. Сравнение результатов расчётов и экспериментов осуществлялось в [8, 10–12], причём в [8, 10] удалось достичь приемлемого соответствия части исследуемых характеристик. Анализ распыла топлива методом объёма жидкости в случае низкоперепадных форсунок в [13–16] проводился при условии задания на выходе из форсунки давления, равного атмосферному. В [14, 16] вычислялась окружная неравномерность распыла топлива на грубых расчётных сетках, а в [13, 15] определялись скорости и диаметры капель на мелких сетках. В работе [16] сопоставление результатов расчёта с экспериментальными данными носило качественный характер. В [13, 15] получено приемлемое количественное соответствие.

Для того чтобы представить процесс распыла топлива в низкоперепадной центробежной форсунке на крейсерском режиме, проведена серия расчётов: в трёхмерной постановке на двух расчётных сетках с максимальными линейными размерами ячеек 100 и 50 мкм и на пятиградусном секторе форсунки на трёх расчётных сетках с максимальными линейными размерами ячеек 25, 12,5 и 6,25 мкм; в осесимметричной постановке на четырёх сетках с максимальными линейными размерами ячеек 6,25, 3,125, 1,5625 и 0,78125 мкм [17]. Сеточной сходимости, которая требуется для признания результатов надёжными [18], удалось достичь лишь при расчёте в осесимметричной постановке [17]; эти результаты и описываются в настоящей статье. Цель работы состояла в том, чтобы найти качественное соответствие между тем сценарием процесса распада, который установлен из расчёта, и классификацией, описанной в [5]. Геометрия исследуемой центробежной форсунки разработана сотрудниками АО «ОДК–Авиадвигатель» и защищена патентом РФ, выданным в 2018 году.

2.    Постановка задачи и метод решения

Рассмотрим течение в низкоперепадной центробежной форсунке, в которой отсечём часть, содержащую шнеки и завихрители. В результате получим осесимметричную геометрию, показанную на рисунке 1. На основании мгновенного распределения скоростей в форсунке исследуемое течение можно условно разделить на пять зон: течение рядом с внутренней поверхностью внешнего завихрителя воздуха (зона 1 ), застойная зона ( 2 ), закрученный поток газа из центрального канала ( 3 ), зона смешения потоков ( 4 ) и зона обратных токов ( 5 ).

Профили скоростей (см. Рис. 2), отвечающие границам A и B на рисунке 1, взяты из расчёта распыла керосина в полной трёхмерной постановке на грубой расчётной сетке с ячейками размером 100 мкм и с их двукратным дроблением на границах раздела [19]. На границе С зададим давление 3476140 Па. Объёмную долю керосина на входе (граница B) определим согласно условию:

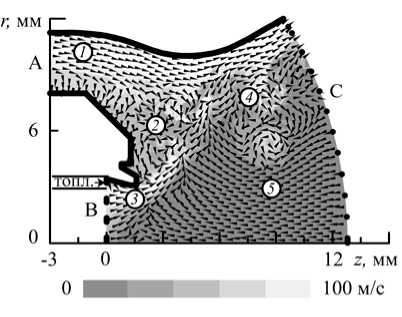
Рис. 1. Геометрия задачи и мгновенное поле скоростей в форсунке (оттенки серого цвета показывают распределение модуля вектора полной скорости, стрелки – направления её радиальной и аксиальной компонент)

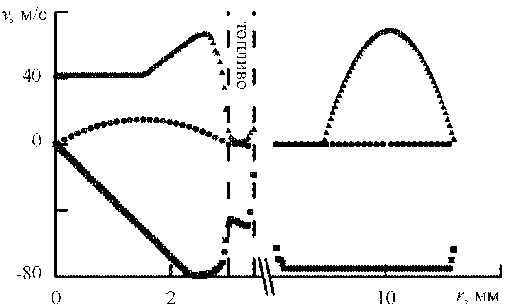
Рис. 2. Зависимости аксиальной (треугольники), радиальной (кружки) и азимутальной (квадраты) компонент скорости на входе в расчётную область

1, r >  3,045,

0, r < 3,045, где r — радиальная координата, измеряемая в миллиметрах. Через вход A керосин не подается, поэтому его объёмная доля на этой границе обнуляется. Плотности керосина и воздуха считаем равными 788 и 13,2 кг/м3, а их вязкости — 0,001003 и 1,7894 10-5 кг/(м·с) соответственно. Коэффициент поверхностного натяжения примем следующим: 0,027 Н/м.

Описанная задача исследовалась методом объёмов жидкости в двухмерной (осесимметричной) постановке с не равной нулю азимутальной скоростью. В рамках этого подхода численно решается система уравнений в частных производных, состоящая из уравнений для импульса смеси:

—pv + V- (pvv) = -Vp + V- [n(Vv + (Vv)T)] + F,

и для объёмной доли жидкости а :

д „ ,— а +V- (av) = 0, dt

где p — плотность, v — скорость, p — давление, п — динамическая вязкость смеси, F — сила поверхностного натяжения, V — оператор набла, T — знак операции транспонирования.

Уравнения, связывающие физические параметры смеси с физическими параметрами составляющих её компонентов, имеют вид:

p = ap w + (1 -a)p g, П = ап w + (1 -а)п g,

где p w и p _g — плотности керосина и воздуха, п w и п g — динамические вязкости керосина и газа.

Для представления силы поверхностного натяжения применим модель непрерывных поверхностных сил:

2p kVa F = о-------,

p g +p w

k = V- n ,     n ^Va ,

I Va|

где о — коэффициент поверхностного натяжения.

Далее при численном решении для дискретизации уравнений использовались схемы первого порядка (First Order Upwind и First Order Implicit), для исключения ситуации, когда неоднородное решение из-за дискретизации может вести себя как однородное, прибегали к методу PRESTO (PREssure STaggering Option) [20]. Для согласования полей скоростей и давления применялся полунеявный метод для уравнений со связью по давлению (Semi-Implicit Method for Pressure-Linked Equation, SIMPLE). Градиенты вычислялись с помощью подхода Least Squares Cell-Based Gradient, для реконструкции границы раздела фаз использовался метод PLIC (Piecewise Linear Interface Calculation) [21], который также иногда называется Geo-Reconstruct. Расчёт проводился в модуле коммерческой лицензионной программной системы конечно-элементного анализа.

3.    Первичный распад плёнки и волны на её поверхности

Результаты моделирования поведения топливной плёнки демонстрирует рисунок 3. Он свидетельствует, что возникновение волн связано с развитием неустойчивости Кельвина– Гельмгольца. Этот вид неустойчивости обусловливается скачком скоростей на границе раздела. Отметим, что согласно рисунку 2, для неустойчивости Кельвина–Гельмгольца характерны две моды: аксиальная и азимутальная. Примерно двукратное превышение перепадом аксиальной скорости на границе раздела керосин/воздух перепада азимутальной составляющей указывает на то, что аксиальная мода — главная, и она в значительной степени будет определять размер сгустков керосина. Наложение осевой симметрии приводит к тому, что азимутальная мода подавляется, и в расчёте моделируется развитие только главной моды неустойчивости. Если бы удалось учесть эволюцию азимутальной моды, то волна была бы направлена не точно по оси O z , а под небольшим углом к ней.

Неустойчивость Кельвина-Гельмгольца в центробежных форсунках может приводить к разным видам первичного распада плёнки. Например, ускоренный поток воздуха сдирает капли с поверхности пленки. Этот тип распада численно исследовался в [22]. Оказалось (см. Рис. 3), что в низкоперепадной форсунке неустойчивость Кельвина–Гельмгольца не успевает развиться в степени, достаточной для реализации подобного сценария. Другой вид первичного распада плёнки состоит в том, что после срыва с кромки движение плёнки в радиальном направлении приводит к её истончению; при этом области между пучностями, возникшими из-за развития неустойчивости Кельвина–Гельмгольца, быстрее истончаются до нулевой толщины; как следствие, пучности превращаются в сгустки керосина. Именно так происходит первичный распад плёнки в низкоперепадной форсунке.

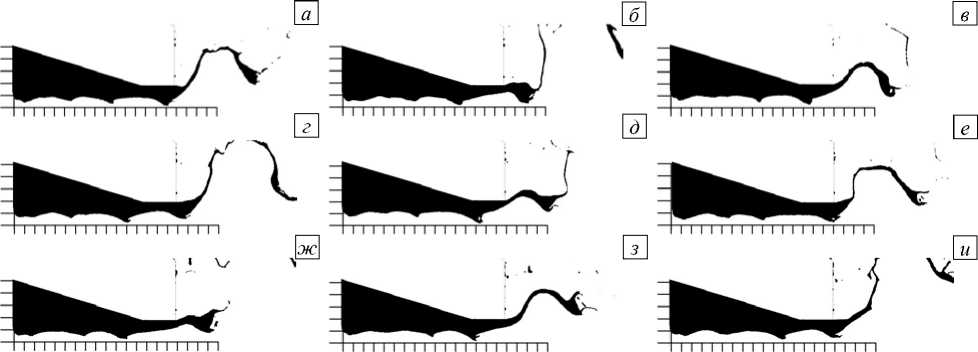
Рис. 3. Поведение плёнки керосина во времени с шагом 12 мкс ( а )–( и ) при расчётной сетке с ячейкой 1,5625 мкм; расстояние между рисками по обеим осям 100 мкм

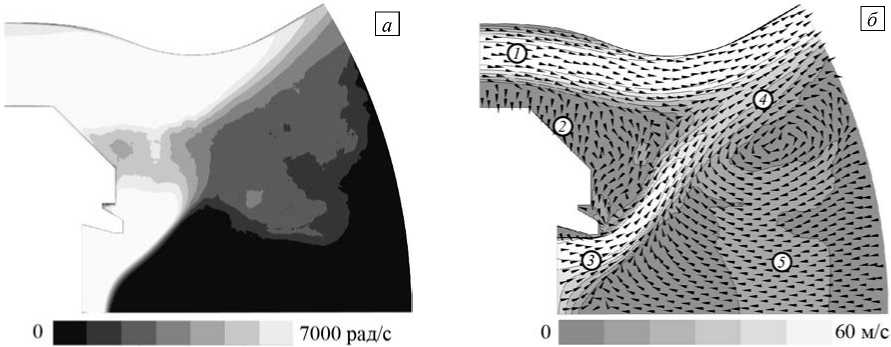
Рис. 4. Усредненные по времени поле угловой скорости (а) и векторное поле Nvr2+ vz2 радиальной и аксиальной компонент скорости (б) (поле показано оттенками серого цвета, а стрелками – направления компонент)

Кроме двух описанных сценариев, возможны и другие; часть из них не осуществима из-за наличия застойной зоны (зона 2 , Рис. 4). Её образование является индивидуальной особенностью исследуемой форсунки и приводит к нейтрализации влияния на первичный распад, оказываемого течением рядом с внутренней поверхностью внешнего завихрителя воздуха (зона 1 ). При отсутствии застойной зоны плёнка оказалась бы зажатой между двумя потоками воздуха, и это привело бы к появлению дополнительных сценариев распада плёнки, обусловленных разницей в скоростях течений из центрального канала (зона 3 ) и внешних завихрителей воздуха.

Распад плёнки, в котором присутствует влияние исключительно закрученного течения из центрального канала, исследовался в [5]. Хотя эксперименты в [5] проводились на воде при нормальных условиях на выходе из низкоперепадной форсунки, режим, обозначенный в [5] как распад перфорированной жидкой плёнки (perforated sheet breakup), качественно соответствует тому, что наблюдается в расчёте. В [5] он характеризуется образованием ячеистой структуры (тонких жидких плёнок, разделённых пучностями) и перфорацией тонкой жидкой плёнки. Несмотря на качественное согласование режимов, имеется существенное количественное отличие: в расчётной структуре обнаруживается всего 1–2 ячейки, в то время как на полученных из эксперимента фотографиях видно значительно бо́льшее их количество. Это можно интерпретировать так: описанные в [5] режимы при увеличении скорости в центральном канале переходят друг в друга без скачков, а в следующем режиме плёнка распадается в непосредственной близости от кромки. Отсюда можно сделать вывод о том, что в расчёте реализуется режим, который является переходным от перфорирования жидкой плёнки к её распаду на сегменты (в [5] — segmented sheet breakup).

После распада плёнки сгустки керосина двигаются двумя группами: первая из них образует внешний конус распыла — А, вторая — внутренний — Б (см. Рис. 5). Из рисунка 6 можно сделать вывод, что истончение плёнки между пучностями приводит к отрыву от неё крупных элементов, которые уносятся потоком газа из центрального канала (зона 3 , см. Рис. 4 б и Рис. 6). Таким образом формируется внутренний конус распыла, переносящий 80% массы керосина.

При разрушении плёнки помимо крупных элементов возникают и мелкие. Часть из них оказывается в застойной области, вдали от потока из центрального канала. Здесь элементы двигаются по инерции и смещаются в радиальном направлении до тех пор, пока не оказываются захвачеными течением рядом с внутренней поверхностью внешнего завихрителя воздуха (зона 1 , Рис.4 б ). В результате этого образуется второй конус распыла (конус A, Рис. 5).

Отметим, что бо́льшая часть показанных на рисунке 5 траекторий относится к области, в которой реальная картина движения керосина не отражается, так как его сгустки распались уже на отдельные капли. Тем не менее, разлёт капель по двум направлениям определяется особенностями разрушения плёнки и наблюдается не только в двухмерном, но и в трёхмерном расчёте [17].

Рис. 5 . Распределение усредненной по времени объёмной доли керосина для расчётной сетки с ячейкой 0,78125 мкм

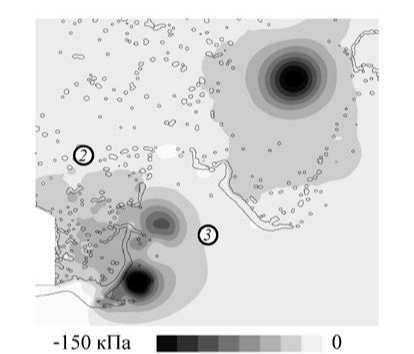
Рис. 6. Распределение мгновенных значений дифференциального давления относительно давления, заданного на выходе из расчётной области с показанными границами раздела

Рис. 7. Найденное в расчёте положение плёнки в форсунке для воды и воздуха при нормальных условиях на выходе из форсунки в разные моменты времени с шагом 20 мкс ( а )–( г ); на ( г ) точками показано нормированное положение плёнки в эксперименте [23]; расстояние между рисками по обеим осям 1 мм

Реализация описанного выше режима распада плёнки в решаемой задаче обусловлена параметрами воздуха и жидкости. Если задать эти параметры такими же, как в [5], то будет иметь место режим, изображённый на рисунке 7, который в [5] называется распадом, вызванным волной (wave-assisted breakup). Характеризующая его волна быстро нарастает при удалении от кромки плёнкообразующей поверхности. Отметим, что при таких значениях параметров жидкости и газа возникновение второго конуса распыла в расчёте не выявлено.

Результатам вычислений, показанным на рисунке 7, отвечает газовое число Рейнольдса

Re g = p g V z D i/ n g = 20800,

(средняя аксиальная скорость газа — v _z ~ 52 м/с, диаметр центрального канала — D_i ~6 мм), и число

Вебера

We w = P ¹² h w ^ = 220

(средняя аксиальная скорость керосина — v _z ~ 12 м/с, толщина плёнки — h_w ~ 110 мкм). В [23] авторы, они же авторы работы [5], приводят фотографию эксперимента по распылу воды для Re g = 19687 и We _w = 216 . Эти значения достаточно близки к значениям, взятым в расчёте. Форма поверхности плёнки с фотографии приведена на рисунке 7 г . Можно видеть, что в эксперименте также наблюдается характерная нарастающая волна. Таким образом, при близких значениях чисел Рейнольдса и Вебера и в расчёте, и в эксперименте реализуется распад, вызванный волной.

Следует отметить, что на рисунке 7 полученные экспериментально координаты положения плёнки были нормированы на величину h_wh_e , где h_e ~ 650 мкм — толщина плёнки в эксперименте. Необходимость выполнения этого была обусловлена тем, что в расчёте толщина отличалась от экспериментальной, а длина нераспавшейся плёнки считалась пропорциональной этому параметру [24]. Разница в углах распыла (Рис. 7) в значительной степени также связана с отличием постановок задачи в расчёте и эксперименте. В частности, для оценки влияния толщины плёнки на угол раствора конуса распыла а можно использовать формулу из теории Танасава и Кобаяси [25]:

k           D 2

а = 2 arc tan ,       , k =----•----, l-k2       D 2 + h где D — диаметр центрального канала, h — толщина плёнки. Теория была построена в приближении потенциального течения для высокоперепадных форсунок, и поэтому она даёт завышенные значения в исследуемом случае: а/2 = 52° — для форсунки из эксперимента, и а/2 = 74° — для форсунки из расчёта. Тем не менее, эти значения подтверждают то, что разница в углах, приведённых на рисунке 7, обусловлена разными постановками задачи. Но, несмотря на отличия, порождающие количественные несоответствия, близость безразмерных параметров — чисел Рейнольдса и Вебера — приводит и в расчёте, и в эксперименте к одинаковым режимам распада плёнки.

4.    Сеточная сходимость

Стандарт Американского общества инженеров-механиков для валидации и верификации в вычислительной гидродинамике [18] рекомендует проводить также исследование сеточной сходимости. В рамках этого в [17] показано, что сеточной сходимости по среднему заутеровскому диаметру в рассматриваемой задаче можно достичь только на сетке с размером ячейки из диапазона 1,5625–3,125 мкм.

Из рисунка 8 можно сделать вывод, что при размере ячейки, бо́льшем 3,125 мкм, в системе не появляется волна, связанная с развитием неустойчивости Кельвина–Гельмгольца, которая определяет первичный распад плёнки при течении через топливную форсунку. При этом качественное изменение поведения поверхности плёнки исчезает только при уменьшении размера ячейки сетки до 1,5625 мкм. Значит, можно сделать вывод, что именно необходимость правильного описания первичного распада в результате развития неустойчивости Кельвина–Гельмгольца привела к тому, что сеточной сходимости по заутеровскому диаметру в [17] удалось добиться только на сетке с ячейкой 1,5625–3,125 мкм.

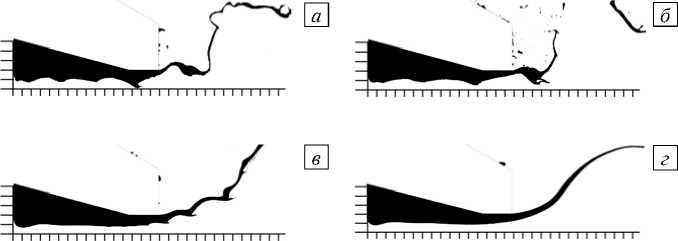
Рис. 8. Поведение плёнки керосина для расчётной сетки с ячейкой разного размера, мкм: 0,78125 ( а ); 1,5625 ( б ); 3,125 ( в ); 6,25 ( г ); расстояние между рисками по обеим осям 100 мкм

5.    Заключение

Изучен распад плёнки при одном из режимов, создаваемых в низкоперепадной центробежной форсунке в условиях, которые близки к реализующимся на крейсерском режиме работы авиадвигателя. Исследованный в форсунке режим характеризуется образованием застойной зоны, которая нивелирует влияние течения из внешних завихрителей на первичный распад плёнки. Классификация режимов распада плёнки после её срыва с кромки для подобного многофазного течения была проведена в [5] экспериментально на установках, в которых нельзя повышать давление на выходе из форсунки от атмосферного значения до 3 МПа.

Установлено, что развитие неустойчивости Кельвина–Гельмгольца приводит к распаду топливной плёнки по сценарию, который качественно отвечает режиму с перфорированием жидкой плёнки при переходе его в режим распада плёнки на сегменты в соответствии с классификацией из [5].

Обнаружено, что, в отличие от распада топливной пленки, полученного в [5], в низкоперепадной форсунке он сопровождается отбросом части сгустков керосина в радиальном направлении.

Показано, что размер ячейки, при котором в решаемой задаче достигается сеточная сходимость, обусловлен следующим: при его бо́льших значениях на поверхности топливной плёнки не развивается неустойчивость Кельвина–Гельмгольца.