Численное моделирование распространения полуэллиптической трещины усталости на основании оценки накопления повреждений

В элементах конструкций, подвергающихся действию переменных нагрузок, могут содержаться начальные трещиноподобные дефекты — полости в сварных соединениях, коррозионные язвы и другие. Трещины усталости, источниками которых являются эти дефекты, могут привести к катастрофическому разрушению конструкции.

Для оценки остаточного ресурса элементов фюзеляжа самолета, сварных соединений судов, трубопроводов и других конструкций в инженерной практике широкое распространение получил метод конечных элементов. Подобные расчеты [1], как правило, производятся в рамках линейно-упругой механики разрушения (ЛУМР), и при этом моделируется развитие трещины, имеющей правильную эллиптическую форму [2, 3]. Однако фронт трещины сохраняет эллиптичность далеко не всегда, что подтверждается экспериментом [4]. Согласно устоявшейся методологии допускается наличие начальной трещины, вычисляются значения коэффициентов интенсивности напряжений (КИН) в нескольких точках фронта, а затем для заданного числа циклов при помощи интегрирования уравнения Пэриса определяются приращения трещины в направлениях, соответствующих этим точкам, и выстраивается новый контур фронта. Эффектом неполного раскрытия трещины обычно пренебрегают ввиду сложности его учета.

Между тем, некоторые исследования показывают, что константы уравнения Пэриса могут зависеть от направления интегрирования, следовательно, прогноз фронта становится некорректным [5, 6], оценки долговечности слабо согласуются с экспериментальными данными. Также осложняется применение КИН из-за различия напряженных состояний в различных точках фронта: например, во внутренней точке полуэллиптической трещины наблюдается плоская деформация, в то время как в наружных точках — плоское напряженное состояние

В связи с ограниченностью возможностей ЛУМР конкурирующим инструментом в вопросе представления пространственных трещин усталости может стать механика поврежденной среды. Эффективность прогнозирования положения фронта трещины и скорости его продвижения при помощи моделирования накопления повреждений была подтверждена недавними исследованиями [7, 8]. Например, в [9] анализ распространения полуэллиптической трещины базировался на оценке накопления повреждений и использовании малоциклового критерия разрушения Коффина. Расчет повреждения производился в двух главных направлениях роста трещины. Однако при постановке задачи были использованы не только данные малоцикловых испытаний, но и интерполяционные формулы определения значений КИН для полуэллиптической трещины в растягиваемой пластине, полученные в [5].

В данной работе предлагается подход к описанию распространения двумерных трещин, основанный на конечно-элементном моделировании (КЭМ) накопления повреждений и деформационном критерии разрушения. Отвечающая ему методика обладает рядом преимуществ перед методикой, общепринятой в ЛУМР. Во-первых, благодаря ей появляется возможность рассматривать трещины, провоцируемые любым начальным дефектом, при неустановившемся фронте трещины, или даже при отсутствии исходной трещины. В качестве причины возникновения трещины может выступать, например, различие в сопротивлении материала усталостному разрушению на уровне микроструктуры. Поэтому начальная фаза распространения трещины и фаза устойчивого подрастания считаются единым процессом, управляемым постепенным накоплением повреждений. Во-вторых, использование деформационного критерия позволяет изучать распространение трещины при развитой пластической деформации. В-третьих, можно принимать во внимание накопленное повреждение в пределах постоянно эволюционирующей области пластической деформации.

Впервые идея применения накопления повреждений при оценке развития трещин усталости была сформулирована достаточно давно [10, 11], однако лишь недавно она была распространена на случай пространственных трещин. В отличие от предшествующего исследования [8], в настоящей работе рассмотрены изменение податливости материала при накоплении повреждений и эффект раскрытия трещины.

2.    Методика моделирования накопления повреждений

В соответствии с разработанным подходом область распространения трещины разбивается на конечные элементы одинаковых размеров. Предполагается, что эти «элементы материала» (далее элементы) представляют собой некоторое число зерен с приблизительно одинаковой ориентацией плоскостей скольжения. Поведение элемента перед вершиной трещины представляется упрощенно как деформирование образца при одноосном напряженном состоянии [12]. Процесс развития трещины усталости заключается в последовательном разрушении элементов согласно закону накопления повреждений и выбранному критерию разрушения. Разрушение элемента имитируется искусственным уменьшением его жесткости на несколько порядков по сравнению с жесткостью окружающего материала. Соответственно, размер элемента является шагом приращения длины трещины в конкретной точке фронта. Так как формирование фронта трещины подчинено конфигурации сетки, представленный подход может применяться только для моделирования трещин с заранее заданным направлением подрастания. Моделирование продвижения трещины посредством удаления конечных элементов широко распространено при анализе хрупкого и квазихрупкого разрушения, гораздо реже — при знакопеременном нагружении для трещины усталости [7].

Упругопластическое поведение материала элементов описывается обобщенной циклической кривой, получаемой из стандартных испытаний образцов при одноосном напряженном состоянии (Рис. 1) [13]. Используется модель кинематического упрочнения материала и критерий пластичности Мизеса.

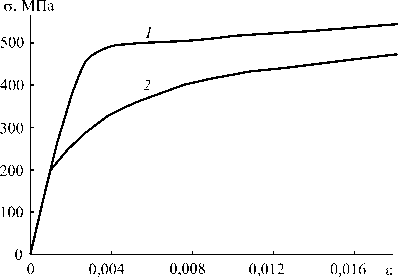
Рис. 1. Монотонная (линия 1 ) и обобщенная циклическая ( 2 ) кривые деформирования стали BS 4360 50D [13]

В качестве критерия разрушения элементов берется деформационный критерий Коффина– Мэнсона, учитывающий вклад в процесс разрушения микропластической деформации, что является актуальным при многоцикловой усталости [14]:

Аб = Аб p + Аб e = CN-а + BN-в,         (1)

где Аб , Абp, Абe — размахи, соответственно, полной, пластической и упругой деформации в направлении, перпендикулярном фронту трещины; N — число циклов до разрушения образца, определяемое обычно по искажению «восходящей» части циклической кривой и резкому увеличению его податливости при возникновении трещины;

C = 0,622 , а = 0,618, B = 0,006 , в = 0,14 — параметры исследуемого в данной работе материала — стали

BS 4360 50D [13].

На начальном шаге расчета анализируется поле деформаций элементов, лежащих в области распространения трещины, и выделяются те из них, в которых развивается пластическая деформация. Эти элементы могут лежать в вершине начального выреза, а при его отсутствии ― в области концентрации напряжений; тогда индикатором начала разрушения может служить изначально введенная неоднородность в сопротивлении переменному нагружению. Затем с помощью деформационного критерия (1) устанавливается число циклов до разрушения каждого элемента Ni , и из них выбирается наименьшее значение n1 , соответствующее наиболее напряженному элементу. Для всех элементов вычисляется накопленное на начальном шаге повреждение согласно выбранному закону накопления повреждений. У наиболее напряженного элемента его значение становится равным единице:

Са =

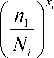
где x i — параметр нелинейности. В случае x i = 1 накопление повреждений является линейным. Количественная оценка параметра нелинейности будет приведена в 4-м разделе.

После начального шага рассчитывается обновленное напряженно-деформированное состояние и определяется число циклов до разрушения следующего элемента с учетом повреждения, накопленного им на начальном шаге. Когда трещина достигает некоторого элемента и повреждение становится критическим, этот элемент выключается из работы, действующие на него усилия перераспределяются между окружающими элементами. Итоговое значение повреждения «элемента материала» является суммой повреждений, накопленных им за все предшествующие циклы. Закон суммирования повреждений может иметь нелинейную форму, например, предложенную С. Марко и В. Штарки [15]:

и

ij

I      iamal            -хр            ,

j I Nj J

где n_j — число циклов до разрушения наиболее «слабого» элемента на j -м шаге подрастания трещины, обусловленное его накопленным повреждением; Nⁱ_j — число циклов до разрушения i -го элемента на j -м шаге подрастания трещины, вычисляемое с помощью деформационного критерия разрушения (1).

В связи с развитием повреждения «элементы материала» у вершины трещины утрачивают способность сопротивляться нагрузке, снижаются их упругие характеристики, изменяется циклическая диаграмма деформирования, что подтверждается испытаниями образцов при крайне малоцикловой усталости [16]:

E , = (1 - d , ) E . (3)

Увеличение податливости материала (3), связанное с его разрыхлением, по-видимому, характерно лишь для сильно поврежденных областей у вершины трещины. При таком состоянии, предшествующем разрушению, накопление повреждений в материале может происходить с увеличивающейся интенсивностью. Изучение явления накопления повреждений в областях с различной интенсивностью деформирования требует дальнейших экспериментальных исследований.

Элементы описанной методики учета накопления повреждений подсказаны работами [9–12] и другими. В этих исследованиях, однако, не использовался метод конечных элементов. К тому же поле деформаций у вершины трещины описывалось приближенно, а оценка роста трещины производилась только при плоском напряженном состоянии.

3.    Моделирование эффекта раскрытия трещины

Известно, что в пределах некоторой части цикла трещина остается закрытой даже при пульсирующем растяжении. Вероятно, впервые это обнаружил В. Элбер, проводивший испытания тонких алюминиевых пластин при различных коэффициентах асимметрии нагружения [17]. Развитие повреждения, по-видимому, не может происходить в течение той части цикла, когда трещина закрыта. Некоторая доля размаха деформации (нагрузки) оказывается «неэффективной», не способствующей развитию разрушения. В данной работе влияние неполного раскрытия трещины описывается с помощью корректирующего параметра раскрытия U , идентичного предложенному Элбером:

Аб eff = UАб .

Экспериментальное определение параметра U для полуэллиптических трещин вызывает значительные сложности из-за труднодоступности внутренних точек фронта. Кроме того, на параметр раскрытия оказывает влияние значительное число второстепенных факторов таких, как депланация фронта, шероховатость поверхностей берегов, образование продуктов окисления у вершины трещины, которые трудно поддаются моделированию.

Как правило, при конечно-элементном методе нахождения параметра раскрытия трещины в плоской задаче считается, что трещина открывается в тот момент, когда в противоположных узлах берегов, ближайших к вершине трещины, напряжения становятся положительными. Однако в работе [18] показано, что такой подход неточен, и для идентификации «точки раскрытия» достаточно отслеживать изменение знака узловой силы в направлении, перпендикулярном плоскости трещины в ее вершине (Рис. 2 a ). Применимость этого соображения и к процессу закрытия полуэллиптических трещин установлена в результате численного изучения контакта берегов трещины. Вычисленные значения параметра раскрытия трещины оказались несколько завышенными по сравнению с экспериментальными [19].

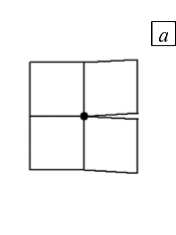
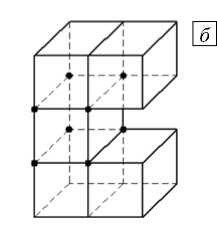
Рис. 2. Положение определяющих узлов для вычисления параметра раскрытия трещины

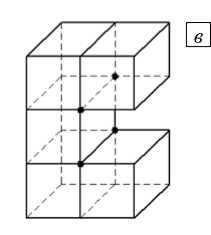
Когда вершина пространственной трещины моделируется в виде прямоугольника, по-видимому, возможно нахождение момента закрытия трещины по изменению знака среднего напряжения в направлении, перпендикулярном плоскости фронта, в узлах элемента, лежащего либо перед вершиной (Рис. 2 б ), либо только в узлах вершины трещины (Рис. 2 в ). Для проверки этого предположения выполнен расчет параметров раскрытия двух полуэллиптических трещин размерами a и c (соответственно глубина и половина ширины) в компактном образце в двух характерных точках (1-я — самая глубокая точка, ей отвечает индекс a ; 2-я — одна из двух симметричных точек на поверхности образца, ей отвечает индекс c ); в таблице для сравнения приведены соответствующие экспериментальные значения.

Таблица. Параметры раскрытия трещины

Номер трещины	Размеры трещины, мм	Положение точки	Эксперимент [20]	Число определяющих узлов в модели
				8	4
			Значение параметра раскрытия трещины
1	a = 3,8 c = 4	Внутри, U a	0,83	0,92	0,88
		На поверхности, U c	0,73	0,75	0,73
2	a = 6,2 c = 8	Внутри, U a	0,87	0,90	0,86
		На поверхности, U c	0,76	0,75	0,71

Результаты показали, что предпочтительным является определение параметра раскрытия трещины по изменению знака среднего перпендикулярного фронту напряжения в четырех узлах вершины трещины. Хорошее соответствие вычисленных значений экспериментальным данным свидетельствует о первостепенном влиянии пластичности на неполное раскрытие трещины. Полученные небольшие расхождения в пределах 6% могут быть вызваны спецификой механизма раскрытия трещины, а также недостаточным объемом экспериментальных данных.

4.    Результаты моделирования

Предложенный подход, основанный на КЭМ накопления повреждений с учетом эффекта раскрытия трещины, применен для исследования развития полуэллиптической трещины в компактном образце (Рис. 3). В соответствии с экспериментальными данными, трещина распространялась от начального электроэрозионного надреза размером 1,88 х 2,6 мм [20]. Образец подвергался постоянной циклической нагрузке, близкой к пульсирующему растяжению ( P min = 1,3 кН; P max = 25 кН). При достижении трещиной ширины 4 мм производилось однократное догружение, которое выразилось в увеличении амплитуды наибольшего значения действующей нагрузки в два раза (в дальнейшем перегрузка), которое не учитывалось при моделировании, амплитуда нагружения считалась постоянной.

В программную систему ANSYS 14.5 включалась разработанная конечно-элементная модель (Рис. 4), подробно детализирующая область развития трещины в образце. Размер элементов у вершины трещины соответствовал толщине начального надреза — 0,2 мм. По мере роста трещины анализировалось напряженно-деформированное состояние элементов у вершины трещины; последовательно оценивалось разрушение элементов по рассчитанному значению эффективного размаха деформации (4) и деформационному критерию разрушения (1).

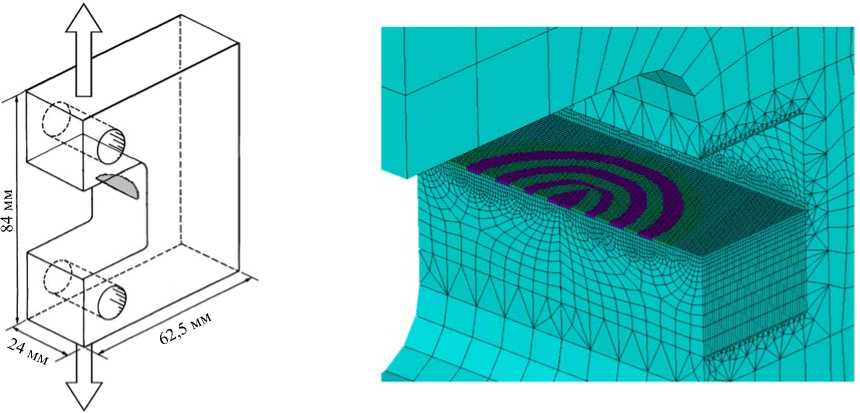
Рис. 3. Компактный образец с полуэллиптической Рис. 4. Вид конечно-элементной дискретизации расчетной трещиной [18] области и эволюция фронта трещины

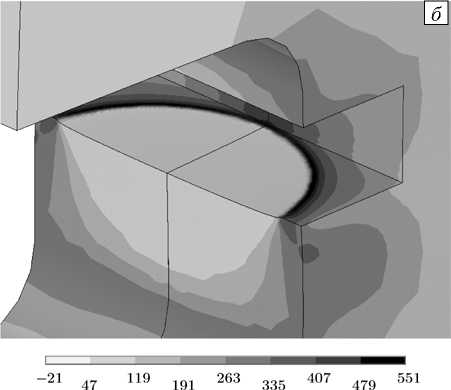
Установленное численно поле наибольших главных напряжений в разрезе по плоскости фронта трещины у начального надреза (Рис. 5 а ) показывает, что развитие трещины начинается в центральной части надреза. На заключительной стадии роста трещины наибольшие напряжения увеличиваются примерно в два раза (Рис. 5 б ), между фронтом трещины и боковыми поверхностями образца образуются зоны значительных пластических деформаций.

Предполагалось, что накопление повреждений имеет нелинейный характер, описываемый соотношением (2). Значение x_i определялось на момент перегрузки на основании сопоставления числа циклов, полученного экспериментально и путем вычислений. Скорость роста трещины до перегрузки хорошо согласуется с экспериментальными данными при значении x i = 0,5, поэтому для параметра нелинейности в отсутствие перегрузки условно было выбрано именно это значение при дальнейшем описании накопления повреждений. По-видимому, параметр нелинейности следует находить из эксперимента на стандартных образцах при изменяющейся по мере испытания амплитуде нагружения.

Полученная эволюция контура фронта хорошо согласуется с экспериментальными данными — в начале роста наблюдаются резкое выравнивание фронта и стремление к предпочтительной полуэллиптической форме (Рис. 4).

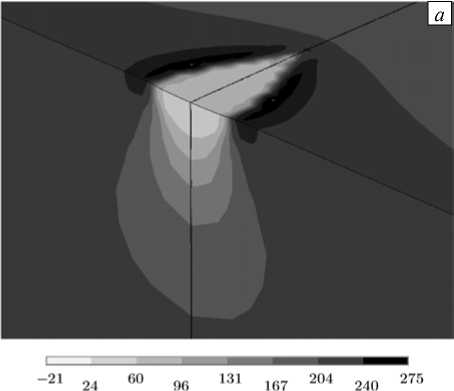
Рис. 5. Распределение наибольших главных напряжений, МПа: в окрестности начального надреза ( a ), в окрестности вершины трещины ( б )

Известно, что перегрузка способна вызывать значительные остаточные напряжения, которые влияют на дальнейшее распространение трещины. Возникающие остаточные напряжения сжатия перед вершиной трещины задерживают ее подрастание; темп роста восстанавливается после релаксации этих напряжений (Рис. 6, темные маркеры). Ярко выражено влияние перегрузки и на соотношение размеров трещины (Рис. 7, светлые маркеры). В статье [20] приводится прогноз развития трещины при отсутствии перегрузки (Рис. 7, пунктирная линия). Зависимость размеров трещины, полученная при КЭМ накопления повреждений без учета перегрузки, имеет монотонный характер (Рис. 7, квадратные маркеры), что согласуется с прогнозируемой зависимостью (Рис. 7, пунктирная линия).

По мере роста трещины градиенты изображенных зависимостей размеров трещины от числа циклов позволяют сделать вывод об изменении скорости ее распространения в разных направлениях (Рис. 6). Очевидно, что перегрузка тормозит продвижение трещины в обоих направлениях, поэтому график становится практически горизонтальным. Это замедление наблюдается в течение примерно 300 000 циклов, после чего влияние остаточных напряжений ослабевает, и градиент вновь начинает интенсивно расти. Поэтому зависимость, полученная по результатам КЭМ без перегрузки, не содержит горизонтального участка. Однократная перегрузка приводит к увеличению времени распространения трещины примерно на 30%.

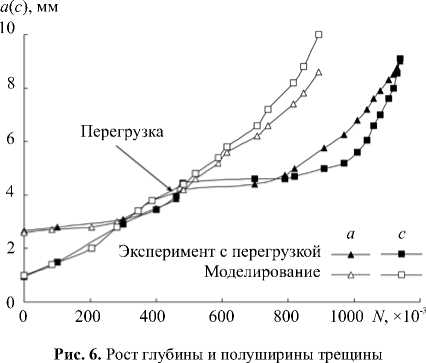
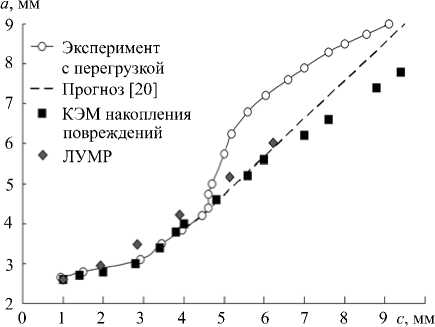
Рис. 7. Зависимость глубины трещины a от ее полуширины c

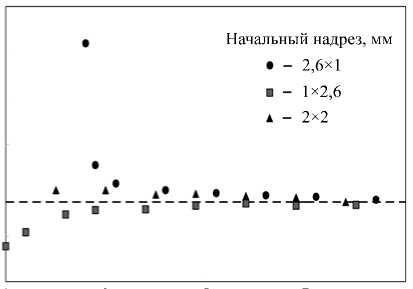
Многие экспериментальные исследования показывают, что при распространении полуэллиптической трещины после некоторой начальной стадии соотношение ее размеров стабилизируется [3, 21, 22]. Поэтому конфигурация начального надреза практически не оказывает влияния на эволюцию фронта, который довольно быстро выравнивается. Этот эффект проиллюстрирован на примере трещин в компактном образце при двух различных надрезах (Рис. 8). Как видно из рисунка 9, соотношение размеров трещин быстро достигает значения ≈ 0,87 и в дальнейшем изменяется слабо.

Рис. 8. Вид контура фронта с ростом трещины

а /с, мм 3,0

2,5

2,0

1,5

1,0

0,5

а, мм

Рис. 9. Соотношение размеров трещины по мере ее роста

5.    Оценка эволюции фронта трещины в рамках ЛУМР

Анализ развития трещин усталости традиционно производится с использованием аппарата ЛУМР и, как правило, с оценкой значений КИН в заданных точках контура фронта трещины. При плоском начальном надрезе сложной формы для получения корректной эволюции фронта необходимо рассмотреть множество направлений развития трещины. Однако, если предположить, что фронт трещины сохраняет свою эллиптическую форму, достаточно ограничиться двумя направлениями — вглубь и по поверхности. Для основных направлений непрерывно по мере роста трещины оцениваются значения размахов эффективных КИН — ⁽A K ) ff , соответствующих моде нормального раскрытия за один цикл нагружения. Развитие трещины может быть описано системой дифференциальных уравнений Пэриса:

^ = C ^ ) f -l = C (^ )f -

где C = 1-48 - 10 ^s - m = 2-86 — параметры материала — стали BS 4360 50D [20].

Нагружение части образца, содержащего трещину, сочетает растяжение и изгиб, поэтому в соответствии с принципом линейной суперпозиции и определением эффективного КИН по Элберу [17]

( ^Ka ) f = U ( A K T + A K .B )- ( A K - ) ff = U - ( A K ^ + A K -b )-

K,- l max

U. =                   (l = a; c) - l K - K lmax где Kmax , Kmin , Kop — КИН, соответственно, максимальный и минимальный в цикле, а также в момент раскрытия трещины. Параметры раскрытия трещины в данном расчете приближенно считались постоянными (Ua = 0-85 - Uc = 0-745 ), поскольку в эксперименте выявлено, что в точках на поверхности эффект раскрытия более выражен, чем во внутренних, а характеризующие его параметры по мере роста трещины изменяются незначительно (см. Табл.); значения размахов КИН, отвечающих растяжению (индекс T ) и изгибу (индекс B ) пластины конечных размеров с поверхностной полуэллиптической трещиной, находились по интерполяционным формулам, полученным с помощью метода конечных элементов (с погрешностью менее 5%) [23]:

AcrVn a           [ a ]   .. a ]

AKT =--T---- M, + МЛ — + MJ —  g, f,fw-

T                          1        2                 3             g 1^J / W ^-

E ( k )               V t ) v t )

' Г              7    2                 1

A^ в n a             । a । i a ।

^ K B = ^H ryzJ ^{M 4 + M 5} I J I ^{+ M 6} I J I g 2 f ’ 2 ^fW ’

E(k) [ V t) V t) _

П2 !    7      2"\

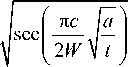
где

I a ।      2

E ( k ) =     1 - 1 —- sin ф d ф — полный эллиптический интеграл второго рода; f_w =

2W о у V c )

При этом коэффициенты зависят: M1-6 — от отношения c/a ; H и g 1,2 — от c/a, aft и ф; f ф1,2 — от c/a и ф; параметрический угол ф отсчитывается от поверхности надреза на образце, перпендикулярной плоскости фронта трещины (0<ф<п); в соответствии с данными эксперимента параметры t = 37 мм, W = 12 мм; размахи номинальных напряжений, вычисленные на основании балочной теории, составляют AcT = 26,7 МПа, AcB = 136,3 МПа (области концентрации напряжений у скруглений компактного образца находятся на значительном расстоянии от области развития трещины (см. Рис. 3) и, как показывает КЭМ, практически не оказывают влияния на рассматриваемые напряжения).

По формулам (6) могут отыскиваться значения размахов КИН в любом направлении развития трещины.

В данном расчете использовались углы ф = л/2 (соответствует (AKa)f — эффективному размаху во внутренней точке) и ф = 0 (соответствует (AKc)f — размаху в наружных точках).

В системе уравнений (5) правые части при подстановке геометрических размеров и параметрических углов представляются в виде функций от a , c , что допускает численное решение системы уравнений с граничными условиями, определяемыми начальными размерами трещины a ₀ = 1 мм, с ₀ = 2,6 мм.

Практически решение системы (5) производилось с помощью программы Mathcad 14. Полученные функции размеров трещины от числа циклов дают возможность оценить последовательность полуэллиптических фронтов трещины. Однако зависимость a ( c ), в силу ограничений применимости интерполяционных формул ( c/W <  0,5), может быть построена только до момента, когда полуширина трещины достигает 6 мм. Эволюция контура фронта, вычисленная в границах ЛУМР с учетом принятых допущений (неизменность параметра раскрытия трещины по мере ее роста, полуэллиптическая форма начального надреза, постоянство констант уравнения Пэриса, точность интерполяционных формул) удовлетворительно согласуется как с данными расчета на основе КЭМ накопления повреждений, так и с экспериментальными данными (Рис. 7). Исходя из возможностей ЛУМР допустимо только частичное моделирование развития трещины, в то время как КЭМ накопления повреждений позволяет следить за ростом трещины вплоть до ее выхода на боковые поверхности образца при развитой пластической деформации материала.

6.    Заключение

В работе выполнено моделирование развития полуэллиптической трещины усталости от начального надреза в стальном компактном образце. Его результаты подтвердили обнаруживаемое в эксперименте резкое стремление фронта трещины к полуэллиптическому контуру в начальной фазе роста. Для оценки развития трещины применялась методика, основанная на КЭМ накопления повреждений, учитывающая эффект раскрытия трещины. При описании циклических свойств материала использовался деформационный критерий разрушения и обобщенная циклическая кривая, получаемые в результате испытаний при одноосном напряженном состоянии. Развиваемая авторами методика позволяет принимать во внимание нелинейный характер накопления повреждений, а также увеличение податливости материала из-за развития повреждения.

При КЭМ пространственной трещины допустимо предположение о том, что трещина открывается в момент, когда среднее значение напряжения в направлении, перпендикулярном фронту трещины, в узлах ее вершины становится положительным (как и в случае плоской задачи). Параметры раскрытия трещины, полученные с учетом этого допущения, для принятых размеров и формы конечных элементов хорошо согласуются с экспериментальными данными. Небольшие отклонения могут быть объяснены недостаточным объемом экспериментальных данных и сложным механизмом раскрытия трещины. Помимо преобладающего воздействия на раскрытие трещины остаточных напряжений, вызванных пластичностью, сюда следует включить окисление берегов трещины и изменяющуюся шероховатость поверхности, влияние которых на процесс раскрытия трещины пока не полностью изучено экспериментально.

Проделанная с целью сопоставления оценка развития трещины в рамках ЛУМР показала, что при корректном определении параметров раскрытия трещины расчет с включением в уравнения КИН дает возможность удовлетворительно прогнозировать эволюцию фронта трещины. Однако по мере приближения трещины к боковым поверхностям образца возрастают пластические деформации, исчезает сингулярность напряжений у вершины трещины, что приводит к некорректным оценкам положения и формы фронта трещины, а следовательно, и долговечности. С помощью численной процедуры моделирования накопления повреждений, в отличие от ЛУМР, наблюдение эволюции фронта трещины осуществимо до поздней стадии развития и при значительных пластических деформациях.

Продемонстрировано, что в условиях деформирования, сочетающих растяжение и изгиб, конфигурация начального надреза мало влияет на развитие трещины. На поздних этапах роста соотношение размеров полуэллиптической трещины асимптотически стремится к фиксированному значению.

Для углубленного понимания характера накопления повреждений в областях с различной напряженностью, а также для оценки влияния поврежденности на изменение податливости материала необходимы дальнейшие экспериментальные исследования.

Работа выполнена при финансовой поддержке РФФИ (проект № 12-08-00943-а).