Численное моделирование роста статической культуры клеток при десорбции факторов роста в порах биореактора

Рост клеточной культуры в пористых скаффолдах зависит от архитектуры пор и распределения факторов роста, включая их десорбцию их пористой матрицы. Математическое моделирование позволяет количественно оценивать влияние геометрии каналов и граничных условий на морфологические и механические характеристики клеточной культуры. Представлена математическая модель роста клеточной ткани в порах скаффолда различной геометрии с учетом десорбции факторов роста из стенок пористой матрицы. Рассмотрены три конфигурации каналов: прямой, синусообразный и градиентнопериодический. В основе модели лежит вершинная модель, позволяющая отслеживать морфометрические, механические и энергетические характеристики каждой клетки во времени. Проведен сравнительный анализ ключевых показателей: темпов роста ткани, среднего фактора формы клеток, нормированной средней площади клетки, потенциальной энергии и распределения максимальных касательных напряжений. Показано, что форма канала существенно влияет на экстремальные значения механических характеристик при сходных средних показателях. Синусообразная геометрия канала приводит к повышенным пиковым значениям энергии, а также более вытянутую морфологию клеток. Прямые каналы обеспечивают более высокие темпы роста на ранних этапах. Градиентнопериодическая форма канала демонстрирует промежуточные значения по темпам роста и ключевым показателям. Полученные выводы могут служить основой для оптимизации архитектуры пористых носителей в тканевой инженерии с целью управления механической нагрузкой и морфологией клеток. Разработанная математическая модель позволяет прогнозировать морфологические и механические отклики клеточной культуры при изменение геометрии пор, что расширяет возможности целенаправленного проектирования скаф-фолдов.

Рост клеточной культуры в структуре скаффолдов является важной задачей в тканевой инженерии и зависит от множества факторов, которые включают топологию пористой матрицы [1], её пористость и проницаемость [1; 2], скорость и структуру потока питательного раствора [2], тип выращиваемых клеток [3; 4] и многие другие. Современные подходы к проектированию скаффолдов учитывают необходимость создания многомасштабной архитектуры, обеспечивающей как механическую поддержку, так и биохимические сигналы для клеток [5]. В данной работе мы фокусируем внимание на эффекте локального высвобождения факторов роста

0000-0002-3229-2330

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

[4] из стенок пористой матрицы. Этот подход к управлению клеточного роста появился недавно и активно внедряется сейчас в технологические процессы. Контролируемая система доставки, встроенная в микроструктуру скаффолда, позволяет стимулировать пролиферацию и активацию клеток именно в зонах контакта ткани со скелетом конструкции [6; 7].

При изучении развития тканей в скаффолдах используют как экспериментальные, так и численные методы, позволяющие анализировать влияние геометрии, механических свойств материала и биохимических стимулов на поведение клеток. Так как большинство процессов в скаффолдах протекают в режиме «черного ящика», особенно важную роль в исследованиях играет математическое моделирование, которое позволяет верифицировать гипотезы, предсказывать динамику роста тканей и оптимизировать характеристики скаффолдов еще на этапе их проектирования. Комбинирование экспериментальных данных с вычислительными моделями позволяет создавать более точные прогностические инструменты для тканевой инженерии [8]. Существует несколько классов моделей. Вершинные модели ( vertex models ), где каждая клетка представлена многогранником (в двумерном случае – многоугольником), а динамика вершин определяется энергетическим функционалом, учитывающим давление внутри клетки, ее площадь, периметр, межклеточные напряжения и др. [9; 10]. Эти модели позволяют учесть соседские перестройки, деления и делaминaцию, обладают гибкостью для адаптации под разные биомеханические условия и относительно легко интерпретируются с биологической точки зрения. Встречаются и модернизированные вершинные модели. Так, в работе [11] представлена вершинная пузырьковая модель. Авторы построили модель с учетом кривизны клеточных границ и представили алгоритм ее моделирования. Клеточно-центровые модели ( cell center models ), где клетки моделируются как агенты с центрами и потенциалами взаимодействия, часто используемые для описания миграции, хемотаксиса, роста и пролиферации. В работе [12] для моделирования ткани был использован подход epi-scale . Такой подход описывает клетку из набора частиц, которые составляют ее внешнюю оболочку и внутреннюю часть. Возникает необходимость прописывать потенциал взаимодействия для всех частиц, внутренних и внешних. Это усложняет разработку модели, но позволяет описывать клетку на различных пространственных масштабах. Сравнивая результаты моделирования работ [12] с недавней работой [13], где при моделировании используется классическая вершинная модель, можно заключить, что результаты моделирования качественно и количественно соответствуют друг другу. Континуальные или гибридные модели, основанные на уравнениях диффузии, реакции и механике сплошных сред. Такие модели эффективны на макроуровне, но плохо описывают индивидуальные клеточные взаимодействия. Модели, основанные на методах молекулярной динамики

[14], в которых клетки представлены как сферы (в двумерном случае – окружности). Основным недостатком таких моделей перед вершинными моделями является наличие пустого пространства между клетками.

Вершинные модели дают подробную картину клеточного уровня, но являются вычислительно дорогими при большом числе клеток [15; 16]. Континуальные модели менее затратны вычислительно, но упускают клеточный детейлинг. Гибридные модели представляют баланс между точностью и масштабом, но сложны в реализации и настройке параметров.

Рост ткани стимулируется десорбцией факторов роста (например, bFGF , EGF , BMP ), которые включают в биомиметические материалы или микросферы, закрепленные на поверхности скаффолда [17]. Их высвобождение может регулироваться временем, пространственной локализацией, химическими и физическими параметрами носителя [7; 18]. Например, онкальные исследования показывают, что EGF , иммобилизованный на поверхности, сохраняет биологическую активность и стимулирует миграцию эпителиальных клеток и пролиферацию в условиях in vitro и in vivo [18].

Несколько исследований демонстрируют важность геометрии пор и доставки факторов роста. Исследование Yilgor et al . [19] показывает, что остеоиндуктивное действие BMP -2 и BMP -7 в скаффолдах повышало костеобразование и регенерацию дефектов у животных, особенно в зонах с открытыми пористыми структурами. Исследование [20] с использованием эластиновых трубок и bFGF : десорбция bFGF стимулировала in vivo -проникновение клеток, образование микрососудов и подавляла кальцификацию, что важно для сосудистых конструкций. Работа [21] с нанофибровыми скаффолд-матрицами: изученное влияние размера пор на проникновение клеток и активацию роста in vivo показывало, что более крупные поры (> 300 мкм) способствовали проникновению костных клеток, тогда как зоны с плотными порами (6–20 мкм) больше подходили для фибробластов. Современные исследования показывают, что оптимальная архитектура скаффолда должна варьироваться в зависимости от типа целевой ткани и специфических требований к механическим свойствам и массопереносу [22].

Несмотря на существующие экспериментальные подходы, интеграция механики взаимодействия ткани, геометрии скаффолда и пространственно-временного распределения факторов роста остаются недостаточно исследованными на клеточном уровне. Вершинная модель представляет собой мощный инструмент для описания клеточной архитектуры, механических взаимодействий и влияния физиологических стимулов, таких как десорбция факторов роста. Именно поэтому комбинированный подход на базе вершинной модели, дополненный десорбцией и диффузионными процессами факторов роста, имеет большой потенциал для системного анализа роста клеточной культуры в разнообразных по форме порах скаффолда.

Разнообразие моделей (вершинные, клеточноцентровые, континуальные) позволяет выбирать подходящий метод в зависимости от целей исследования. Подход вершинной модели особенно перспективен для описания клеточной динамики, формы, давления и механических взаимодействий. Десорбция и контролируемый выпуск факторов роста из стенок скаффолда играет ключевую роль в стимулировании тканевого роста, что подтверждено в многочисленных in vivo -исследованиях. Однако почти отсутствуют модели, сочетающие детальную геометрию пор, биомеханику клеток и кинетику факторов роста. Это пробел, который мы заполняем в данной работе.

Как известно, клеточная культура, растущая в скаффолдах, не обладает свободной подвижностью, которая обычно присуща мезенхимальному фенотипу клеток [23]. Последние обычно появляются под влиянием ткани, которая отдает специальную команду отдельным клеткам к активным действиям, чтобы решить определенную задачу. Например, закрыть рану или повысить иммунитет организма. Раковые клетки также относятся к мезенхимальному фенотипу, но ровно по обратной причине – они стараются выбраться из-под контроля здоровой ткани и активно перемещаются в поисках подходящих условий для роста опухоли. Культура, которая формируется в скаффолде, не является еще полноценной тканью, поэтому активности не проявляет. В этом смысле ее фенотип ближе к эпителиальному.

Эпителий представляет собой компактный слой высокоорганизованных клеток, прикрепленных к базальной мембране и лишенных межклеточного вещества. Благодаря плотной упаковке и выраженной полярности, клетки взаимодействуют друг с другом посредством молекул адгезии и формируют сплошной барьер, отделяющий внутреннюю среду организма от внешней. Эти клетки не обладают свободной подвижностью, что определяет их эпителиальный фенотип, противоположный мезенхимальному, при котором клетки теряют контакт с соседями и становятся способными к миграции – например, в процессе канцерогенеза или регенерации ран.

Форма, положение и поведение клеток определяются балансом сил внутри ткани. Одним из ключевых источников внутренних механических напряжений является цитоскелет [24], в частности актиновая кора, которая создает натяжение на мембранах клеток и способствует их взаимодействию как друг с другом, так и с внеклеточным матриксом. При этом эпителий может подвергаться механическим воздействиям извне: со стороны базальной мембраны, внеклеточного матрикса или соседних тканей.

С целью моделирования механики и динамики такой ткани мы используем двумерную вершинную мо- дель, в которой каждая клетка описывается как многоугольник, а вершины (отмечены зелеными точками на рис. 1) этих многоугольников определяют ее форму и положение [25–27]. Из всех возможных правильных покрытий плоскости наиболее подходящим в биомеханическом смысле является шестиугольная упаковка – она минимизирует механическую энергию и обеспечивает наилучшее приближение к круглой форме. Эффективность вершинных моделей для описания морфогенетических процессов подтверждается их успешным применением в различных биологических контекстах [28].

В основе модели лежит предположение, что поведение клеток в ткани определяется стремлением всей системы минимизировать потенциальную энергию U ( t ). Суммарная энергия ткани описывается как сумма вкладов от всех клеток:

N ( t )

U ( t ) = E

n ( A ( t )- A0 )2 +

+ m P ² ( t ) +

n ⁽ t )                                  .

+-E( Ut)-1о )2 + j=1

n ⁽ t )                                      .

+ фЕ( aj ( t )- a0 )

j = 1

Потенциал (1) впервые был введён в работе [29] и затем проверен на задачах морфогенеза [13; 26; 27]. Каждое слагаемое имеет физический смысл и отражает специфический тип клеточного взаимодействия или ограничения, обусловленные тканевой архитектурой.

Первое слагаемое отвечает за сопротивление клеток изменениям своей площади. Биофизически это соответствует внутреннему гидростатическому давлению, под-

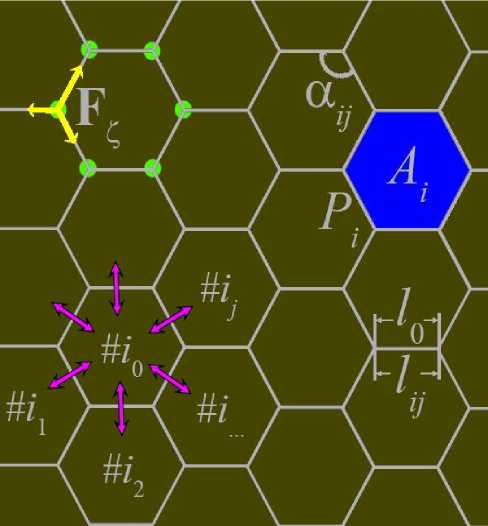
Рис. 1. Схематическое представление клеток математической модели держиваемому цитоплазмой и ограниченному клеточной мембраной. Клетка стремится сохранять объем, а в двумерной модели – площадь A0. Отклонение от «эталонной» площади A0 приводит к увеличению потенциальной энергии, что стимулирует возврат к равновесию. Параметр η определяет жесткость объемного сжатия клетки и коррелирует с упругостью клеточной мембраны и механическими свойствами цитоскелета.

Второе слагаемое моделирует контрактильную активность кортикального актина, расположенного под мембраной клетки. Сила, создаваемая этим актиновым кольцом, действует по периметру клетки, способствуя ее округлению. Чем выше коэффициент μ, тем сильнее клетка стремится минимизировать длину своей границы. Биологически это связано с активностью сократительных белков, таких как миозин II, которые обеспечивают сжатие клеточной мембраны.

Третье слагаемое отвечает за стремление клеточных ребер (границ между клетками) сохранять длину, близкую к эталонному значению l 0 . С позиции биологии, это связано с прочностью адгезионных контактов между клетками, в частности, с плотностью кадгериновых соединений. Удлинение или укорочение ребер приводит к нарушению межклеточной адгезии и требует энергетических затрат. Параметр σ определяет жесткость адгезионного контакта.

Четвертое слагаемое регулирует отклонение углов клеточного многоугольника от идеального значения α0 = 2π / 3, характерного для шестиугольной упаковки. Биофизически оно связано с сохранением формы клетки и равномерной передачей механических напряжений по всем направлениям. Большие отклонения от равномерной геометрии могут указывать на локальные перегрузки или деформации в ткани. Коэффициент φ определяет степень угловой жесткости клетки и может зависеть, например, от состояния цитоскелета или плотности межклеточных контактов.Все четыре слагаемых взаимодействуют и обеспечивают баланс между механической стабильностью и адаптивностью ткани. Такая энергетическая модель позволяет точно описы- вать локальные деформации, клеточные перестройки и реакции на внешние воздействия.

Эволюция ткани реализуется через перемещение вершин клеток под действием механических сил (отмечены желтыми стрелками на рис. 1), возникающих из градиента потенциальной энергии:

F = -

d U ( t ) d R

В условиях высокой вязкости клеточной среды инерционными эффектами можно пренебречь, поэтому уравнение движения узлов формулируется в аристотелевской форме:

V - kF.. H (I F - F o ) . (3)

где: k – коэффициент подвижности; H – функция Хэви-сайда; F 0 – критическое значение силы, ниже которого вершина остается неподвижной.

Для моделирования пролиферации вводится стохастический механизм деления (рис. 2), зависящий от числа вершин в клетке:

n ( t ) - 6

p d. ⁽ t ) = p о q .

где p 0 и q – параметры модели.

Деление инициируется при достижении клеткой определенной геометрической конфигурации. Алгоритм деления включает:

• 1.    Поиск самого длинного и противоположного ему.

• 2.    Добавление новых вершин в центры этих ребер.

• 3.    Образование нового ребра между ними.

• 4.    Обновление топологии.

Еще один важный механизм – это интеркаляция.

Это процесс клеточной перестройки, при котором соседние клетки изменяют топологические связи, перераспределяя свои границы. В результате происходят локальные изменения формы и плотности клеток, что позволяет ткани адаптироваться к внешним и внутренним воздействиям без увеличения общего числа клеток.

Интеркаляция играет ключевую роль в таких процессах, как: удлинение тканей (конвергентное удлине-

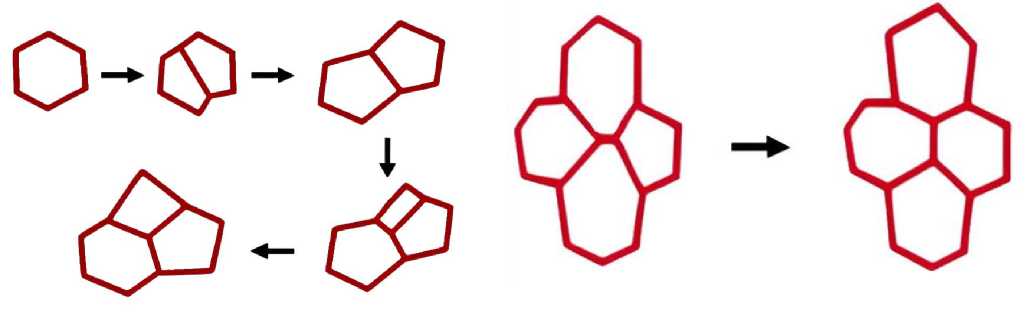
Рис. 2. Схематическое представление процесса деления клеток

Рис. 3. Схематическое представление процесса интеркаляции клеток

ние в эмбриогенезе), зарастание ран, перераспределение клеток при морфогенезе органов, адаптация к механическим нагрузкам. Она обеспечивает гибкость и пластичность ткани, сохраняя при этом ее целостность.

В модели интеркаляция реализуется при выполнении геометрического условия: если длина ребра l ij между двумя соседними клетками становится меньше некоторого критического значения d int . Это указывает на локальное накопление напряжения или «избыточность» данного ребра. Тогда выполняется топологическое перестроение ( T 1-переход):

• 1.    Короткое ребро удаляется.

• 2.    Его вершины перестраиваются, формируя новое ребро, ориентированное перпендикулярно к прежнему.

• 3.    Пересчитываются соседства и обновляется топология клеточного графа.

• 4.    Клетки обмениваются соседями: одна пара клеток теряет общий контакт, другая приобретает.

Этот процесс схематически представлен на рис. 3 и происходит мгновенно по достижению критической длины между клетками.

В ткань вводится диффузионное поле химического фактора (например, кислорода или сигнальных молекул), распространяющееся по соседним клеткам и поглощаемое ими. Обмен химическими сигналами схематически обозначен розовыми стрелками на рис. 1. Процесс описывается системой уравнений:

J (t) = (C(t)- C (t)) 8I, (t) ,(5)

dC (t)   n", ,

= ZJ( t)-в C( t),(6)

dt         j=1 j где δ – коэффициент диффузии, β – скорость деградации вещества, Ci (t) - концентрация в i-й клетке.

Концентрация может влиять на механические свойства клеток, например:

n = n ( C ( t ) ) ; н = н ( C ( t ) ) ;  ° = ° ( c ( t ) ) ,    (7)

что позволяет учитывать хемомеханическую обратную связь. Моделирование взаимосвязи между химическими сигналами и механическими свойствами тканей представляет собой активно развивающееся направление в вычислительной биологии [31].

Разработанная нами математическая модель обладает широкими возможностями для анализа динамики клеточной культуры в масштабах отдельных клеток. Ее ключевое преимущество заключается в том, что она позволяет детально отслеживать полную эволюцию состояния каждой отдельной клетки в составе моделируемого ансамбля от начальной конфигурации и вплоть до конечного момента расчета. В процессе моделирования сохраняется информация о геометрии клетки, ее механических характеристиках, истории делений, топологических перестроек и изменениях концентраций химических факторов, что открывает возможность для комплексного анализа взаимодействия биомеханиче- ских и биохимических процессов. Число клеток, которое может быть включено в расчет, ограничивается только объемом доступных вычислительных ресурсов, что делает модель масштабируемой и применимой для задач различного уровня сложности – от небольших локальных фрагментов ткани до протяженных областей с тысячами элементов. По классификации данная модель относится к классу дискретных многоагентных систем, построенных на основе вершинного подхода (vertex model). Этот метод сочетает в себе достаточную строгость математического описания и гибкость настройки под конкретные биофизические условия. Несмотря на относительную концептуальную простоту формализма, модель способна с высокой точностью воспроизводить широкий спектр ключевых явлений клеточной динамики: рост и деление клеток, их перестройки посредством интеркаляции, а также межклеточный обмен химическими сигналами, влияющими на механические свойства ткани. Благодаря такому сочетанию универсальности и точности разработанная Модель может служить эффективным инструментом для изучения закономерностей морфогенеза, оптимизации     характеристик     биоинженерных конструкций и прогнозирования поведения тканей в различных экспериментальных и биомедицинских сценариях.

Результаты математического моделирования

В данном разделе представлены результаты численных экспериментов по моделированию роста статической клеточной культуры в порах скаффолда различной геометрии. Целью моделирования являлось выявление влияния формы канала на кинетику роста, морфологические характеристики клеток и распределение механических напряжений в ткани. Следует отметить, что комплексное изучение взаимосвязи геометрии носителя и клеточного ответа представляет значительный интерес для современной тканевой инженерии [32].

Рассматривались три варианта геометрии пор: прямой, синусообразный и градиентно-периодический каналы. Уравнение (8) описывает форму прямого и синусообразного канала:

y = ± d • ( 1 + e • sin ⁽ K • x )) ,               (8)

где d = 4,5 и ε = 0,5 постоянные величины, а K = 0 для прямого канала и K = 0,25 для синусообразного канала.

Градиентно-периодическая форма канала была задана уравнением (9):

[ cos ( 1,5 n Kx ) sin ( 0,15 n ) +

+ cos ( 0,15 n ) sin ( 1,5 n Ky ) +                   (9)

• + cos ( 1,5 n Ky ) sin ( 1,5 n Kx ) ] 2 - 0,37 < - 0,25,

где K = 0,045.

Во всех вариантах вдоль стенок канала присутствует источник факторов роста, задаваемый уравнением:

Ю dC

= ( C o - C fg ( t ) ) • ( - 0,01 t + 15 ) - a C fg ( t ) ,  (10)

dt где Cо - эталонная концентрация фактора роста на границе, а - коэффициент потребления факторов роста клетками ткани, множитель (-0,011 + 15), отражающий уменьшение интенсивности источника со временем.

Кроме того, на левой границе канала действовал дополнительный источник химического сигнала, интерпретируемый как постоянная подача питательного вещества в статическом биореакторе. В момент времени t = 0 в системе присутствует одна шестиугольная клетка, расположенная вблизи левой границы. Механические и биохимические параметры клеток во всех сценариях одинаковы (таблица), меняется только форма пор. Полученные нами начальные условия и S -образная кинетика роста качественно согласуются с экспериментальными наблюдениями за ограниченным ростом клеточных слоёв in vitro [33]. Важность пространственного градиента факторов роста для направленного морфогенеза дополнительно подтверждается исследованиями in vivo [34].

На рис. 4-6 представлена эволюция ткани в каналах прямоугольной, синусообразной и градиентнопериодической формы через равные промежутки времени. Из представленной на рис. 4-6 динамики видно, что наиболее быстрые темпы роста ткани в каналах прямоугольной и градиентно-периодической формы. Это наблюдение подтверждается графиком, представленным на рис. 7, где показана зависимость изменения количества клеток во времени N(t). Из графика видно, что во всех случаях наблюдается характерная S-образная динамика роста: на начальном этапе (первые 250 единиц времени) рост числа клеток невысокий, что соответствует фазе адаптации ткани к условиям среды.

Механические и биохимические параметры модели

μ	η	σ	φ	A 0	l 0	α 0
0,0	4,0	1,0	1,0	3^3 / 2	1,0	2п / 3

k	F 0	p 0	q	d int
0,5	0,1	5 • 10 -5	1,4	0,15

δ	β	C 0	α
1,0	0,04	20,0	0,04

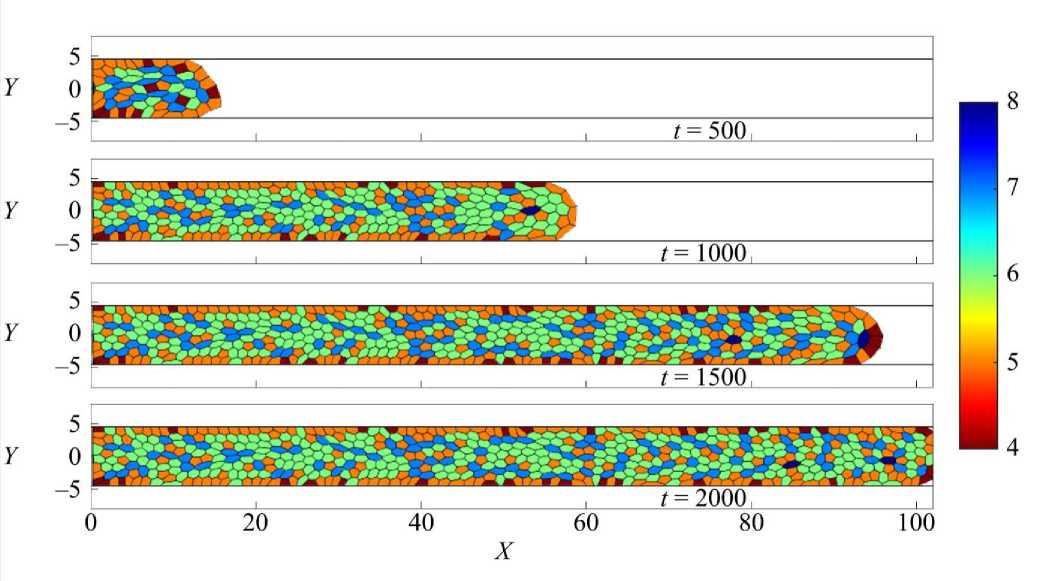
Рис. 4. Результаты численного расчета заполнения прямоугольной поры скаффолда клеточной культурой. Кадры сверху вниз соответствуют последовательным моментам времени. Цветовая шкала показывает распределение клеток по числу сторон. Область заполнения определена уравнением (8) с параметром K = 0

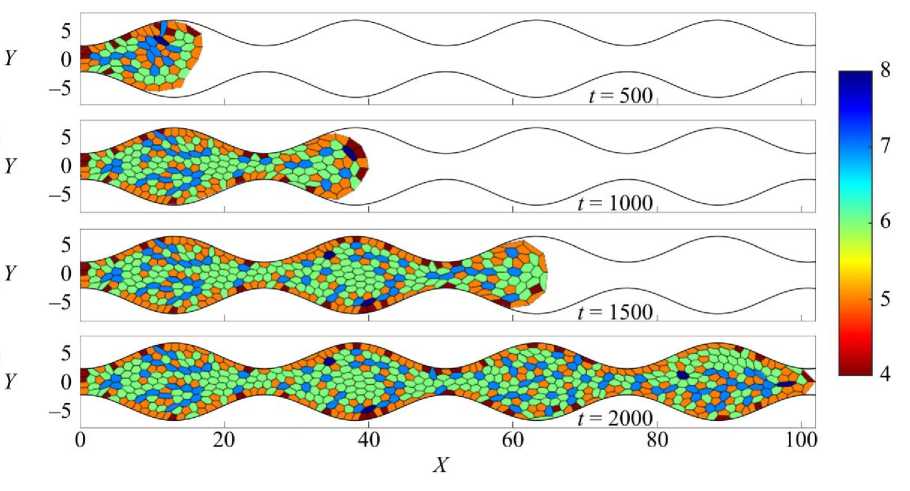
Рис. 5. Результаты численного расчета заполнения синусообразной поры скаффолда клеточной культурой. Кадры сверху

вниз соответствуют последовательным моментам времени. Цветовая шкала показывает распределение клеток по числу сторон. Область заполнения определена уравнением (8) с параметром K = 0,25

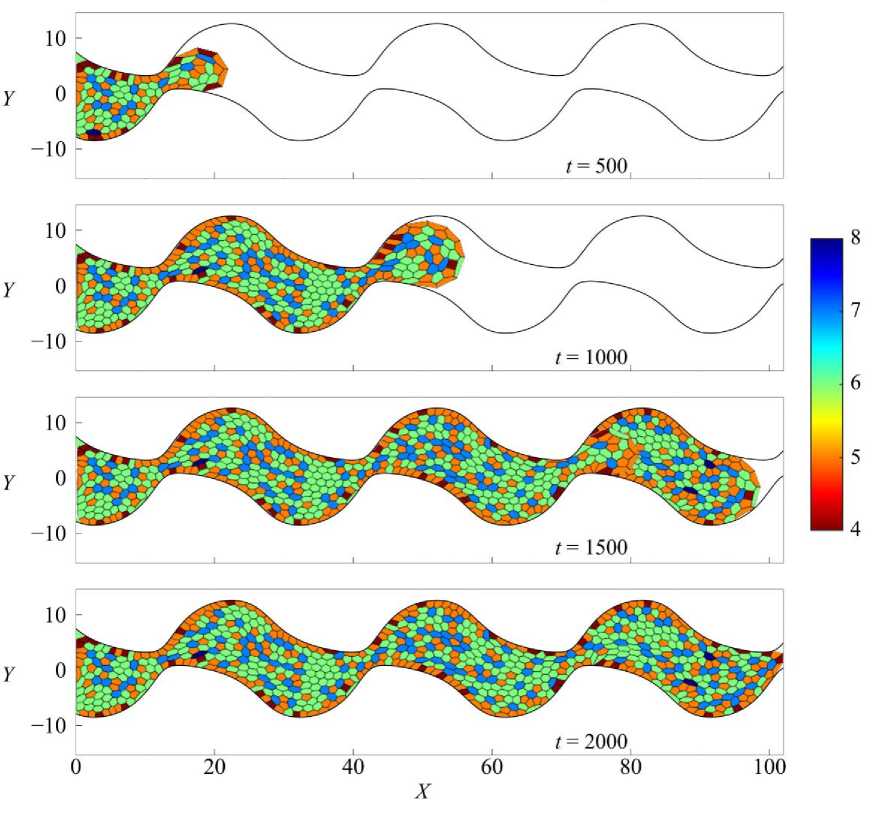
Рис. 6. Результаты численного расчета заполнения градиентно-периодической поры скаффолда клеточной культурой. Кадры сверху вниз соответствуют последовательным моментам времени. Цветовая шкала показывает распределение клеток по числу сторон. Область заполнения определена уравнением (9) с параметром K = 0,045

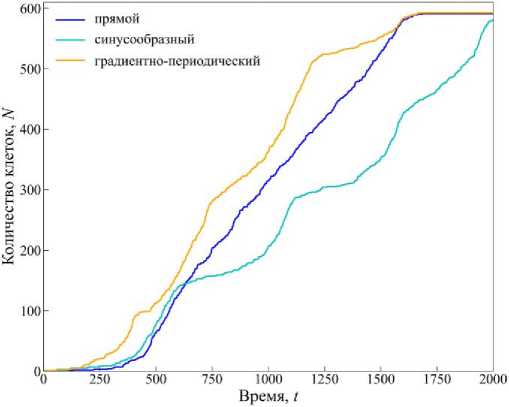
Рис. 7. График зависимости изменения количества клеток со временем N ( t ). Время указано в произвольных единицах

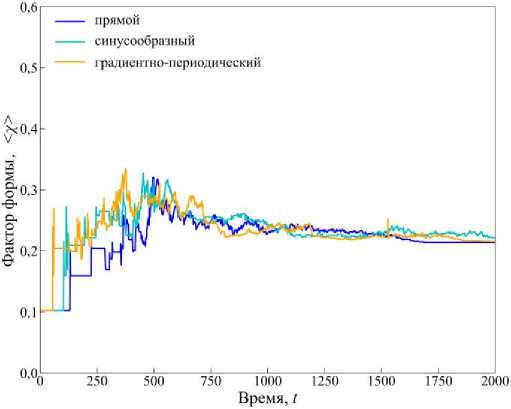
Рис. 8. График изменения среднего значения фактора формы <х( t )>. Время указано в произвольных единицах

Далее следует активная экспоненциальная фаза, где скорость пролиферации максимальна. В завершающей стадии темп роста замедляется, что отражает заполнение пространства поры и ограничение ресурсов. Сравнительный анализ кривых на рис. 7 показывает, что в прямом канале (синяя кривая) рост клеточной ткани идет наиболее равномерно и достигает максимального количества клеток в момент времени t = 1500. Это можно объяснить отсутствием сложных геометрических препятствий для распространения ткани и равномерным распределением факторов роста по всей длине канала.

Подобные эффекты, связанные с влиянием геометрии канала на транспорт и распределение веществ, отмечаются и в других работах, например, в обзоре [35], посвящённом микроканальным системам. В синусообразном канале (голубая кривая) наблюдается более медленный рост, особенно после момента времени t = 500, что связано с изменяющейся шириной канала, создающей участки с локальными концентрационными и механическими градиентами. В градиентнопериодическом канале (оранжевая кривая) темпы роста на всем промежутке времени самые высокие, но по мере заполнения свободного пространства темпы сходятся с темпами роста в прямом канале. Замедление роста ткани можно интерпретировать как эффект сложной структуры стенок, формирующей неравномерное распределение питательных веществ и факторов роста. Таким образом, геометрия пор существенно влияет на кинетику роста культуры, причем простая линейная конфигурация канала создает наиболее благоприятные условия для быстрого заполнения пор.

Обсудим подробнее морфометрические параметры клеток (средний фактор формы, нормированная площадь) и механические показатели ткани (распределение максимальных касательных напряжений и энергия на одну клетку). Рассмотрение этих параметров позволит сопоставить качественные наблюдения с количествен- ными данными и выявить связь между геометрией канала и особенностями роста ткани.

График на рис. 8 иллюстрирует изменение среднего арифметического значения фактора формы <χ> от времени для трех рассматриваемых геометрий пор. Фактор формы для каждой клетки рассчитывается следующим образом:

P 2 ( t ) l ( t ) =   ■        ^{- 1},                   (11)

4пД (t)

где P i ( t ) - периметр и A i ( t ) - площадь клетки. Минимальное значение x ' ( t ) = 0 соответствует идеально круглой клетке, увеличение x ■ отражает удлинение или искажение формы. Для правильного шестиугольника этот параметр имеет значение /₀ ~ 0,103.

Анализ графика показывает, что в каждом типе канала значение <χ(t)> возрастает примерно в 3 раза за первые 500 единиц времени. Такое поведение параметра связано с тем, что система начинает эволюцию с одной шестиугольной клетки. Ее деление приводит к появлению двух пятиугольных клеток, что резко увеличивает параметр . Значения параметра флуктуируют на начальном этапе эволюции из-за небольшого числа клеток в системе. А на протяжении остального времени значение <χ(t)> постепенно уменьшается, ^ 0,2. Поэтому будем рассматривать динамику изменения этого параметра с момента времени t = 500. В прямоугольном канале на протяжении всего процесса роста ткани значение параметра <χ(t)> устремляется ближе всего к минимальному, что указывает на более изотропную и стабильную форму клеток (см. рис. 8, синяя кривая). Вероятно, равномерное механическое окружение способствует поддержанию близкой к кругу конфигурации. Наши вычисления фактора формы хорошо согласуются с подходом, применяемым в вершинных моделях для анализа морфоло- гии тканей [9; 36]. В синусообразном канале параметр <χ(t)> демонстрирует наибольшие отклонения от значения в прямом канале в последние 500 единиц времени (см. рис. 8, голубая кривая). Это можно связать с неравномерным распределением механических напряжений в местах сужения и расширения канала. Подобная анизотропия формы клеток в ответ на геометрические ограничения наблюдалась в экспериментах с микроканаль-ными устройствами [37]. В градиентно-периодическом канале параметр <х( t )> принимает промежуточные значения (см. рис. 8, оранжевая кривая). Вероятно, сложная геометрия пор в данном случае приводит к локальным механическим перегрузкам и вынужденной деформации клеток при их делении и уплотнении. Динамика кривых на рис. 8 также показывает, что по мере заполнения свободного пространства поры ткань стремится к стабилизации своей структуры. Значения <х( t )> во всех трех случаях выходят на стационарный уровень, однако конечные значения зависят от конфигурации канала.

На другом графике (рис. 9) показано изменение фактора формы х( t) для начальной клетки. Наблюдение именно за начальной клеткой позволяет проследить, как изменяется ее геометрия в процессе роста ткани и изменения локального механического окружения. В прямом канале (см. рис. 9, синяя кривая) х( t) колеблется около значения, близкого к хо, что указывает на сохранение формы клетки, близкой к кругу, несмотря на рост и взаимодействие с соседями. В синусообразном канале (см. рис. 9, голубая кривая) значение х(t) остается наибольшим на протяжении всего моделирования, что говорит о значительных и устойчивых деформациях начальной клетки, вызванных периодической и неоднородной геометрией пор, создающей переменные механические нагрузки. А в градиентнопериодическом канале (см. рис. 9, оранжевая кривая) значение параметра х(t) выше, чем в прямом, и демонстрирует более выраженные колебания, что свя- зано с периодическим изменением локального напряженного состояния при заполнении изогнутых участков канала. Таким образом, форма начальной клетки, находящейся в системе с момента инициализации, служит индикатором того, насколько сильно геометрия канала способна влиять на локальную стабильность клеток.

График на рис. 10 отражает изменение нормированной средней площади клеток во времени для трех типов каналов. Под нормированной понимается средняя площадь клеток, деленная на эталонную площадь A ₀ правильного шестиугольника, принятого в модели.

В прямом канале (см. рис. 10, синяя кривая) нормированная площадь быстро стабилизируется близко к значению 0,6 A ₀. В синусообразном канале (см. рис. 10, голубая кривая) стабилизация происходит медленнее, но конечное значение нормированной площади такое же, как и в канале прямоугольной формы. Более медленная стабилизация < A ( t )> обусловлена периодической формой канала. В градиентнопериодическом канале (см. рис. 10, оранжевая кривая) наблюдается наиболее быстрое стремление параметра < A ( t )> к значению 0,6 A 0 .

Но в ходе эволюции клеточной культуры значение < A ( t )> совершает флуктуации, которые с течением времени уменьшаются, что обусловлено геометрией канала. Наиболее быстрая стабилизация < A ( t )> соответствует оптимальной упаковке и равномерному распределению механических напряжений.

График на рис. 11 отражает изменение энергии, приходящейся на одну клетку U 1 ( t ). Видно, что в начальный момент времени в каждом типе канала энергия увеличивается одинаковыми темпами. Но с момента достижения в системе 50 клеток изменение параметра U 1 ( t ) для каждого канала расходится. В прямоугольном канале U 1 ( t ) продолжает монотонно возрастать

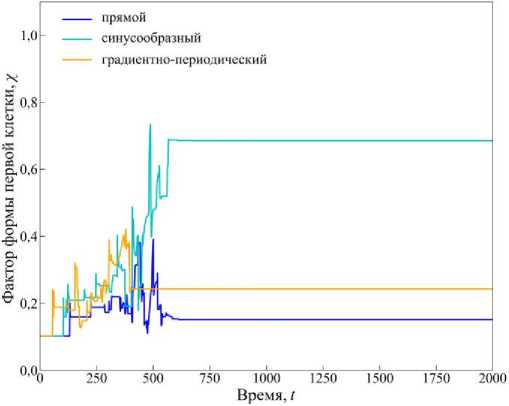
Рис. 9. График изменения фактора формы х( t ) для начальной клетки. Время указано в произвольных единицах

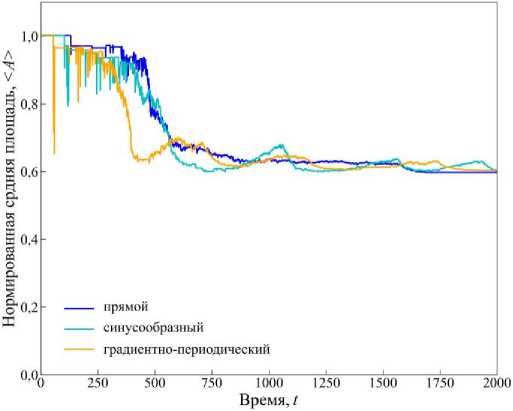
Рис. 10. График изменения нормированной средней площади < A ( t )>. Время указано

в произвольных единицах

(см. рис. 11, синяя кривая). В синусообразном канале рост    U i ( t )  прекращается на некоторое время

(см. рис. 11, голубая кривая). Это связано с тем, что клеточная ткань развивается в узком месте синусообразного канала, где темпы роста ткани замедляются (см. рис. 7, голубая кривая). После прорастания ткани через узкое место канала значение U 1 ( t ) начинает быстро расти, достигая максимального - U 1 ( t ) = 13,1. Затем наблюдается уменьшение этого параметра до значения U 1 ( t ) = 9,9 после которого снова U 1 ( t ) увеличивается с постепенным затуханием амплитуды и стремлением этого параметра к медианному значению U 1 ( t ) = 12. Такое скачкообразное поведение параметра U 1 ( t ) напрямую связано с формой канала скаффолда. А в градиентно-периодическом канале    U 1 ( t )

начинает сразу резко возрастать до медианного значения U 1 ( t ) = 11,6 (см. рис. 11, оранжевая кривая). Затем наблюдается аналогичный сценарий поведения U 1 ( t ) как и в случае синусообразного канала, но с небольшим ростом к медианному значению (см. рис. 11, оранжевая прямая).

Наиболее интересным параметром является распределение максимальных касательных напряжений клеточной ткани в конечный момент времени. Данный параметр позволяет оценить не только значения напряжений, которые возникают в клеточной культуре, но и области  канала, в  которых возможно их накопление. Данная информация является особенно полезной при  разработке  пористых матриц  для выращивания ткани. Рассмотрим каждую форму канала подробнее.

Для того чтобы оценить максимальные касательные напряжения в упругопластической системе, необходимо вычислить собственные значения Х 1 и Х₂ тензора напряжений Коши для каждой клетки. Тензор напряжений о i для каждой i -й клетки рассчитывается по данным координат вершин клетки R ij = ( x ij , y ij ) и силам F ij = ( F ijx , F ij ), действующим на эти вершины, по следующей формуле:

где I - единичная матрица. Подставив (13) в характеристическое уравнение (14) и раскрыв определитель, получим квадратное уравнение:

X ² - (а + а )Х + (а а - а а ) = 0,       (15)

xx       yy               xx yy        xy yx           ,

корни которого:

λ1,2

σ xx

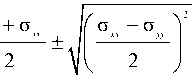
+ а а xy yx ,

и будут собственными значениями Х 1 и Х₂ тензора напряжений о i .

Добавим пару слов о интерпретации собственных значений. Если Х 1 , Х₂ > 0, то будут наблюдаться растяжения в клетке по двум осям, если Х 1 , Х₂< 0, то в клетке наблюдается сжатие по двум осям, а если Х 1 и Х 2 имеют разные знаки, то в этом случае будут наблюдаться сдвиговые деформации. Тогда максимальные касательные напряжения в клетках ткани можно определить следующим образом:

τ max

Х 1 - Х 2

n ( t )

° .=— й R j — R • и .

2 A i   j = 1

Здесь A i - это площадь клетки, R ij - координаты вершины клетки, R i - координаты центра клетки, суммирование ведется по всем вершинам клетки-многоугольника. Поскольку у нас двумерная задача, то тензор о i будет иметь вид матрицы 2*2:

σ

σ xx

σ xy

σ yx

σ yy

,

где а^ и а^ - нормальные напряжения вдоль осей x и у , а а и а - касательные напряжения. Собственные значения Х 1 и Х₂ можно найти, решив характеристическое уравнение вида:

det ( а - X I ) = 0,                  (14)

На рис. 12 представлены карты максимальных касательных напряжений для каждой формы канала в конечный момент времени ( t = 2000).

Для того чтобы провести детальную и объективную количественную оценку пространственного распределения локальных зон, в которых наблюдаются повышенные механические нагрузки внутри ткани, нами был создан специализированный программный инструмент, реализованный на языке программирования Python . Разработка предназначена для автоматизированной обработки карт максимальных касательных напряжений, полученных на основе численного моделирования роста ткани в порах скаффолда, и последующего выделения областей с экстремальными значениями этих напряжений, а также их количественной характеристики.

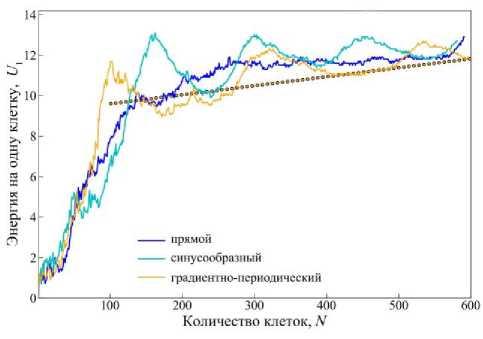
Рис. 11. График изменения энергии на одну клетку U 1 ( t ). Точечная оранжевая линия отражает скользящее среднее значение U 1 ( t ) для градиентнопериодического канала, начиная с момента t = 100

Программный модуль построен таким образом, чтобы минимизировать влияние субъективного фактора при интерпретации данных и обеспечить воспроизводимость анализа. Последовательность выполнения операций включает несколько взаимосвязанных этапов:

• 1.    Загрузка и предварительная обработка: автоматическое считывание изображений, содержащих распределение максимальных касательных напряжений, и их подготовка к последующему анализу.

• 2.    Пороговая сегментация: бинаризация изображения с использованием заданного относительного или абсолютного порога, что позволяет выделить только те участки ткани, где значение напряжений превышает выбранный уровень.

• 3.    Выделение связных областей: идентификация отдельных пятен, представляющих собой локальные зоны концентрации напряжений, и определение их границ.

• 4.    Вычисление характеристик пятен: вычисление площади каждой выделенной области, координат ее центра масс.

• 5.    Визуализация результатов.

Применение данного инструмента позволяет количественно охарактеризовать зоны концентрации касательных напряжений. Это, в свою очередь, открывает возможность численного сравнения τ max конфигураций каналов, выявляя особенности их влияния на распределение механической нагрузки в ткани.

Можно заметить, что в прямом канале (рис. 12, а ) напряжения распределены более менее однородно.

В центре наблюдается скопление локальных пиков касательных напряжений τ max (см. рис. 12 справа). В синусообразном канале (рис. 12, б ) локальные максимумы касательных напряжений τ max совпадают с участками сужения канала. Это очень хорошо видно из карты областей с максимальными касательными напряжениями τ^red > 0,8 τ max (см. рис. 12, справа). Также стоит отметить, что области с максимальными касательными напряжениями τ max в синусообразном канале имеют большие размеры, чем в канале прямой формы. Концентрация механических напряжений в зонах геометрических неоднородностей является известным феноменом в биомеханике тканей и отмечается, в том числе, при исследовании клеточного ответа на топографию субстрата [38]. В градиентно-периодическом канале (см. рис. 12, в ) касательные напряже ния τ max распределены крайне неоднородно. Выделяются локальные участки с высокими значениями, расположенные преимущественно в местах геометрической сложности пор (см. рис. 12, справа). Это свидетельствует о концентрации касательных нагрузок в узких и искривлённых сегментах канала. А области с максимальными касательными напряжениями τ^red > 0,8 τ max в данном типе канала имеют самые большие значения, чем в каналах упомянутых выше. Выявленные закономерности распределения напряжений имеют важное значение для прогнозирования долговечности тканеинженерных конструкций, поскольку циклические механические

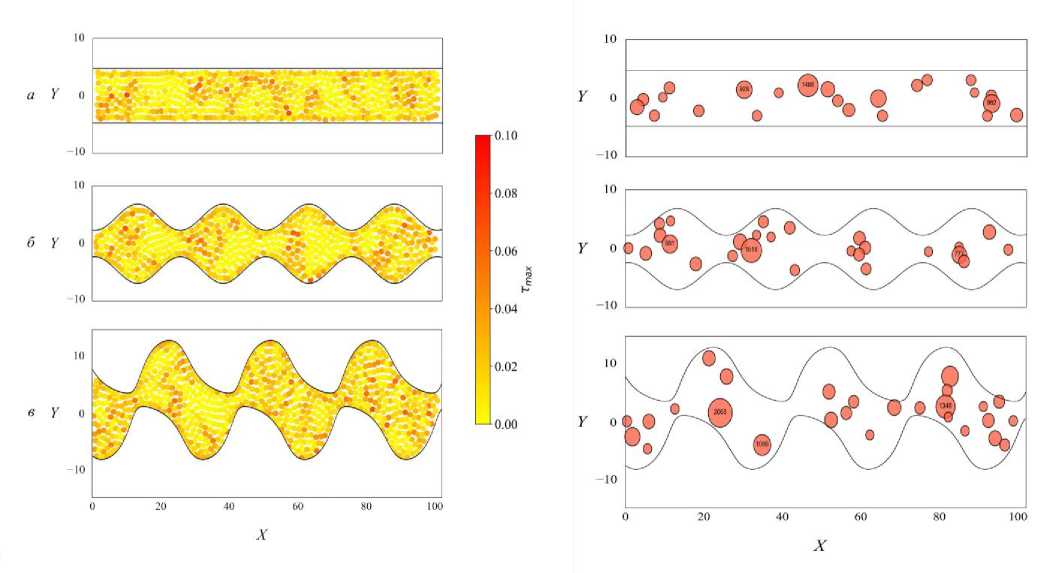
Рис. 12. Слева: карты максимальных касательных напряжений в клеточной культуре в конечный момент времени ( t = 2000) для каждого типа канала: а – прямой; б – синусообразный; в – градиентно-периодический. Каждая точка соответствует центру тяжести клетки. Цветовая шкала показывает значение максимальных касательных напряжений τ max . Справа: карты областей с максимальными касательными напряжениями τ^red > 0,8 τ max

в каналах соответствующей формы. Подписаны три самые большие области, значения приведены в пикселях

нагрузки могут индуцировать ремоделирование внеклеточного матрикса [39].

В данной работе предложена и исследована математическая модель роста клеточной культуры в порах статического биореактора в условиях десорбции факторов роста. Разработанная модель основана на вершинной модели и учитывает широкий спектр факторов, включая геометрические и химические свойства клеток. Математическое моделирование роста клеточной культуры с учетом десорбции факторов роста из стенок скаффолда обеспечило детальное воспроизведение морфометрической и механической динамики.

Полученные результаты показывают, что геометрия пор скаффолда оказывает комплексное влияние как на скорость роста культуры, так и на морфологические характеристики отдельных клеток. Прямой канал обеспечивает наилучшие условия для быстрого увеличения числа клеток и сохранения их формы, близкой к изотропной, что указывает на минимальные локальные механические и геометрические ограничения. Более сложные конфигурации, такие как синусообразные и градиентно-периодические каналы, замедляют рост ткани в статических биореакторах. Также форма канала

• 1.    Design of lattice structures for trabecular-bone scaffolds: comparative analysis of morphology and compressive mechanical behavior / Y. Pirogova, M. Tashkinov, I. Vindokurov, N. Elenskaya, A. Tarasova, A. Shalimov, V.V. Silberschmidt // Biomechanics and Modeling in Mechanobiology. – 2025. – Vol. 24, no. 5. – P. 1535–1564.

• 2.    Numerical analysis of permeability of functionally graded scaffolds / D. Bratsun, N. Elenskaya, R. Siraev, M. Tashkinov // Fluid Dynamics & Materials Processing. – 2024. – Vol. 20. – P. 1463–1479.

• 3.    Research advances on biomaterials for the delivery of growth factors to regulate wound repair / T.T. Weng, C.H. Cai, C.M. Han, X.G. Wang // Zhonghua Shao Shang Yu Chuang Mian Xiu Fu Za Zhi. – 2022. – Vol. 38. – P. 691–696.

• 4.    Growth factor and its polymer scaffold-based delivery system for cartilage tissue engineering / L. Chen, J. Liu, M. Guan, T. Zhou, X. Duan, Z. Xiang // Internaional Journal of Nanomedicine. – 2020. – Vol. 15. – P. 6097–6111.

• 5.    Hollister, S.J. Scaffold translation: barriers between concept and clinic / S.J. Hollister, W.L. Murphy // Tissue Engineering Part B: Reviews. – 2011. – Vol. 17. – P. 459–474.

• 6.    Growth factor release from tissue engineering scaffolds / M.J. Whitaker, R.A. Quirk, S.M. Howdle, K.M. Shakesheff // Journal of Pharmacy and  Pharmacology.  –  2001.  –

  Vol. 53. – P. 1427–1437.

• 7.  Hu, J. Nano-fibrous tissue engineering scaffolds capable of

  growth factor delivery / J. Hu, P.X. Ma // Pharmaceutical Research. – 2011. – Vol. 28. – P. 1273–1281.

• 8.    Implementing Computational Modeling in Tissue Engineering: Where Disciplines Meet / J.N. Post, S. Loerak-ker, R.M.H. Merks, A. Carlier // Tissue Engineering Part A. – 2022 – Vol. 28. – P. 542–554.

• 9.    Vertex models of epithelial morphogenesis / A.G. Fletcher, M. Osterfield, R.E. Baker, S.Y. Shvartsman // Biophysical Journal. – 2014. – Vol. 106. – P. 2291–2304.

• 10.    Брацун, Д.А. Биомеханические модели живой ткани / Д.А. Брацун, И.В. Красняков, А.Д. Брацун // Российский журнал биомеханики. – 2023. – Т. 27, № 4. – С. 50–71.

• 11.    Ishimoto, Y. Bubbly vertex dynamics: A dynamical and geometrical model for epithelial tissues with curved cell shapes / Y. Ishimoto, Y. Morishita // Physical Review E. – 2014. – Vol. 90. – P. 052711.

• 12.    Multiscale computational study of the mechanical regulation of cell mitotic rounding in epithelia / A. Nematbakhsh, W. Sun, P.A. Brodskiy, A. Amiri, C. Narciso, Z. Xu, J.J. Zartman, M. Alber // PLoS Computational Biology. – 2017. – Vol. 13. – P. e1005533.

• 13.    Красняков, И.В. Математическое моделирование ранних процессов морфогенеза эпителиальных тканей / И.В. Красняков, К.В. Костарев, Д.А. Брацун // Российский журнал биомеханики. – 2024. – Т. 28, № 1. – С. 88–100.

• 14.    Effect of substrate heterogeneity and topology on epithelial tissue growth dynamics / M. Mazarei, J. Astrom, J. Westerlund, M. Karttunen // Physical Review E. – 2023. – Vol. 108. – P. 054405.

• 15.    Krasnyakov, I. Cell-based modeling of tissue developing in the scaffold pores of varying cross-sections / I. Krasnyakov, D. Bratsun // Biomimetics. – 2023. –

• 16.    Active vertex model for cell-resolution description of epithelial tissue mechanics / D.L. Barton, S. Henkes, C.J. Weijer, R. Sknepnek // PLoS Computational Biology. – 2017. – Vol. 13. – P. e1005569.

• 17.    Егорихина, М.Н. Скаффолды как системы доставки биологически активных и лекарственных веществ / М.Н. Егорихина, П.А. Мухина, И.И. Бронникова // Комплексные проблемы сердечно-сосудистых заболеваний. – 2020. – Т. 9. – С. 92–102.

• 18.    Design of epidermal growth factor immobilization on 3D biocompatible scaffolds to promote tissue repair and regeneration / T. Bavaro, S. Tengattini, R. Rezwan, E. Chiesa, C. Temporini, R. Dorati, G. Massolini, B. Conti, D. Ubiali, M. Terreni // Scientific Reports. – 2021. – Vol. 11. – P. 2629.

• 19.    An in vivo study on the effect of scaffold geometry and growth factor release on the healing of bone defects / P. Yilgor, G. Yilmaz, M.B. Onal, I. Solmaz, S. Gundogdu, S. Keskil, R.A. Sousa, R.L. Reis, N. Hasirci, V. Hasirci // Journal of Tissue Engineering and Regenerative Medicine. – 2013. – Vol. 7. – P. 687–696.

• 20.    Kurane, A. In vivo cellular repopulation of tubular elastin scaffolds mediated by basic fibroblast growth factor / A. Kurane, D.T. Simionescu, N.R. Vyavahare // Biomaterials. – 2007. – Vol. 28. – P. 2830–2838.

• 21.    In vivo cell migration and growth within electrospun porous nanofibrous scaffolds with different pore sizes in a mouse pouch model / D.C. Markel, T. Bou-Akl, B. Wu, P. Pawlitz, X. Yu, L. Chen, T. Shi, W. Ren // Journal of Functional Biomaterials. – 2025. – Vol. 16. – P. 181.

• 22.    In vitro biomimetic engineering of a human hematopoietic niche with functional properties / P.E. Bourgine, T. Klein, A.M. Paczulla, T. Shimizu, L. Kunz, K.D. Kokkaliaris, D.L. Coutu, C. Lengerke, R. Skoda, T. Schroeder, I. Martin // Proceedings of the National Academy of Sciences. – 2018. – Vol. 115. – P. E5688-E5695.

• 23.    Kalluri, R. The basics of epithelial-mesenchymal transition / R. Kalluri, R.A. Weinberg // Journal of Clinical Investigation. – 2009. – Vol. 119. – P. 1420–1428.

• 24.    Heisenberg, C.-P. Forces in tissue morphogenesis and patterning / C.-P. Heisenberg, Y. Bellaiche // Cell. – 2013. – Vol. 153. – P. 948–962.

• 25.    Красняков, И.В. Математическое моделирование инвазивной карциномы в условиях анизотропии химических полей:  почкование и миграция раковых клеток /

  И.В. Красняков // Российский журнал биомеханики. – 2022. – Т. 26, № 3. – С. 45–58.

• 26.    Красняков, И.В. Исследование процессов переупаковки клеток в эпителиальных листах in silico: часть I. Одноосное растяжение ткани /И.В. Красняков, М.Д. Бузмаков // Российский журнал биомеханики. – 2025. – Т. 29, № 1. – С. 105–118.

• 27.    Красняков, И.В. Исследование процессов переупаковки клеток в эпителиальных листах in silico: часть II. Развитие

  ткани в условиях различных границ / И.В. Красняков, М.Д. Бузмаков // Российский журнал биомеханики. – 2025. – Т. 29, № 3. – С. 11–30.

• 28.    Alt, S. Vertex models: from cell mechanics to tissue morphogenesis / S. Alt, P. Ganguly, G. Salbreux // Philosophical Transactions of the Royal Society B: Biological Sciences. – 2017. – Vol. 372. – P. 20150520.

• 29.    Krasnyakov, I. Mathematical modeling of evolution of cell networks in epithelial tissues / I. Krasnyakov // Quantitative Biology. – 2024. – Vol. 12, Issue 3. – P. 286–300.

• 30.    Alignment of cellular motility forces with tissue flow as a mechanism for efficient wound healing / M. Basan, J. Elgeti, E. Hannezo, W.J. Rappel, H. Levine // Proceedings of the National Academy of Sciences. – 2013. – Vol. 110. –

  P. 2452–2459.

• 31.    Recho, P. Theory of mechanochemical patterning in biphasic biological tissues / P. Recho, A. Hallou, E. Hannezo // Proceedings of the National Academy of Sciences. – 2019. – Vol. 116. – P. 5344–5349.

• 32.    Hutmacher, D.W. Scaffold-based tissue engineering: rationale for computer-aided design and solid free-form fabrication systems / D.W. Hutmacher, M. Sittinger, M.V. Risbud // Trends in Biotechnology. – 2004. – Vol. 22. – P. 354–362.

• 33.    Active wetting of epithelial tissues / C. Perez-Gonzalez, R. Alert, C. Blanch-Mercader, M. Gomez-Gonzalez, T. Ko-lodziej, E. Bazellieres, J. Casademunt, X. Trepat // Nature Physics. – 2019. – Vol. 15. – P. 79–88.

• 34.    Mammoto, T. Mechanical control of tissue and organ development / T. Mammoto, D.E. Ingber // Development. – 2010. – Vol. 137. – P. 1407–1420.

• 35.    Павар, С.А. Применение бифуркации и рекомбинации микроканалов для микрофлюидных приложений: литературный обзор / С.А. Павар, В.К. Чоукси // Российский журнал биомеханики. – 2023. – Т. 27, № 2. – С. 30–46.

• 36.    Motility-driven glass and jamming transitions in biological tissues / D. Bi, X. Yang, M.C. Marchetti, M.L. Manning // Physical Review X. – 2016. – Vol. 6. – P. 021011.

• 37.    Geometric control of cell migration / B. Chen, G. Kumar, C.C. Co, C.C. Ho // Scientific Reports. – 2013. – Vol. 3. – P. 2827.

• 38.    Collective cell durotaxis emerges from long-range intercellular force transmission / R. Sunyer, V. Conte, J. Escribano, A. Elosegui-Artola, A. Labernadie, L. Valon, D. Navajas, J.M. Garcia-Aznar, J.J. Munoz, P. Roca-Cusachs, X. Trepat // Science. – 2016. – Vol. 353. – P. 1157–1161.

• 39.    Latorre, M. Mechanobiological stability of biological soft tissues / M. Latorre, J.D. Humphrey // Journal of the Mechanics and Physics of Solids. – 2019.  – Vol. 125.  –

• 40.    Vining, K.H. Mechanical forces direct stem cell behaviour in development and regeneration / K.H. Vining, D.J. Mooney // Nature Reviews Molecular Cell Biology. – 2017. – Vol. 18. – P. 728–742.

существенно влияет на экстремальные значения морфометрических и механических характеристик растущей ткани, при этом средние значения во времени остаются близкими. Синусообразные каналы создают условия для повышенных пиков давления и энергии, что важно учитывать при проектировании скаффолдов в тканевой инженерии.

Также форма канала существенно влияет на экстремальные значения морфометрических и механических характеристик растущей ткани, при этом средние значения во времени остаются близкими. Синусообразные каналы создают условия для повышенных пиков давления и энергии, что важно учитывать при проектировании скаффолдов в тканевой    инжене рии. Полученные данные согласуются с современными представлениями о важности пространственного распределения механических напряжений для тканевого гомеостаза [40].

Работа вносит вклад в понимание механизмов морфогенеза и регенерации тканей. Разработанная математическая модель может быть применена для решения широкого круга задач, связанных с исследованием механических и химических взаимодействий в многоклеточных системах. Перспективы дальнейших исследований включают разработку более детализированных моделей, учитывающих влияние внешних стимулов, а также их экспериментальную валидацию.

Vol. 8. – P. 562.

P. 298–325.

Финансирование. Исследование выполнено за счет гранта Российского научного фонда № 25-11-00338,

Конфликт интересов. Авторы заявляют об отсутствии конфликта интересов.

NUMERICAL MODELING OF STATIC CELL CULTURE GROWTH DURINGGROWTH FACTOR DESORPTION IN BIOREACTOR PORES

I.V. Krasnyakov, M.D. Buzmakov, D.A. Bratsun

Perm National Research Polytechnic University, Perm, Russian Federation

ARTICLE INFO