Численное моделирование самосогласованной динамики поверхностных и грунтовых вод

DOI:

Подземные воды имеют важное значение при решении практических задач, связанных с определением гидрологических режимов пойменных территорий междуречий и речных долин, водохранилищ и озер, а также других природных и гидротехнических водных объектов. К настоящему времени динамика грунтовых вод и фильтрационных течений хорошо изучена как на основе экспериментальных данных, так и с использованием хорошо известных и апробированных математических моделей (с результами можно ознакомиться, например, в работах [1; 5; 6; 10; 12; 13; 16; 17; 19; 22; 25]). На основе этих моделей разработаны методики (см., например, [18]) по расчету стационарных и нестационарных уровней грунтовых вод, а также расходов и скорости фильтрационных течений, используемых при проектировании гидротехнических сооружений и определения границ зон подтопления в окрестности водных объектов для задач кадастрового учета. Как правило, аналитические формулы, используемые в этих методиках, основаны на решениях линеаризованных уравнений, являющихся некоторыми приближениями исходной нелинейной модели динамики грунтовых вод, что, в свою очередь, приводит к увеличению погрешности расчетов, ограничению класса решаемых задач по геометрии водных объектов и структуре течения, а также требует больших временных затрат при выборе параметров моделей и нормировочных коэффициентов.

В настоящее время важным и мощным инструментом изучения гидродинамических течений в природных и технических системах наряду с физическим экспериментом и аналитическими методами исследования математических моделей является вычислительный эксперимент, основанный на численном решении уравнений гидродинамики хорошо апробированными методами и применении параллельных технологий для повышения производительности расчетов [3; 4; 11; 14; 21; 24; 26].

Целью данной публикации является разработка эффективной методики расчета зон затопления и подтопления на сложном рельефе местности с произвольной геометрией нестационарных водных объектов, основанной на прямом численном интегрировании уравнений нелинейной динамики поверхностных и грунтовых вод. В части 1 описана математическая модель динамики поверхностных и грунтовых вод, а в части 2 — численный алгоритм и структура параллельного вычислительного модуля программного комплекса «EcoGIS-Simulation». Результаты тестовых расчетов в одномерной и двумерной постановках представлены в части 3.

1.    Математическая модель1.1.    Динамика поверхностных вод

Моделирование динамики поверхностных вод осуществляется с учетом всех основных физических и метеорологических факторов: источников воды; рельефа суши и дна водоемов; свойств подстилающей поверхности — придонного трения, инфильтрации (впитывание воды в грунт); внутреннего вязкого трения и ветрового воздействия; вращения Земли — силы Кориолиса; испарения воды. Эти факторы позволяет учитывать модель мелкой воды, основанная на системе уравнений Сен-Венана:

эн

— + V ± (Яu) = q,

д(d^u) + V± (Яu ® u) = —gHV±n + Яf , где b(x, y) — функция рельефа местности; H(x,y,t) = n(x,y,t) — b(x,y) — толщина слоя поверхностной воды; п — уровень свободной водной поверхности; u(x,y,t) = {их,иу} — вектор скорости течения поверхностного слоя жидкости; g — ускорение свободного падения; V± = {д/дх,д/ду} — дифференциальный оператор набла в плоскости (x,y). Величина q = q(s) — q^) — q(e-y) + q^ определяет скорость притока/оттока жидкости за счет действия источников/стоков в поверхностном слое воды, где q(s)(x,y,t) — скорость притока воды через гидротехнические сооружения и за счет осадков; q(m^)(x,y,t) — функция стока из-за просачивания (инфильтрации) в грунт; q(e^) — темп потери воды из-за испарения; q^“p) — скорость высачивания (подъема) грунтовых вод на поверхность. В общем случае для суммарной удельной силы, действующей на слой жидкости в модели мелкой воды, имеем:

f = f _A + f v + f Q + f w + f , (3)

где f _A — сила придонного трения; f _v — сила вязкого турбулентного трения; f _Q — сила Кориолиса; f _w — сила воздействия атмосферных потоков (ветра); f . = qu . /Я — сила воздействия источников/стоков воды q, втекающих/вытекающих в поверхностный слой жидкости со скоростью u . . Более подробное описание удельных сил из (3), действующих на поверхностные воды и используемых в данной работе, дано в [20; 21; 27].

1.2.    Метод расчета динамики грунтовых вод

Важной характеристикой, используемой при описании динамики грунтовых вод, является пористость грунта ψ , которая определяет объем пор в единице объема грунта, то есть ф = 1 — Y s , где Y _s = Q _d /Q _s — относительный объем твердых частиц в единице объема грунта; Q _s — плотность твердых частиц; Q _d — плотностью скелета (сухого) грунта, численно равная массе единицы объема грунта без учета воды в его порах. Наряду с величиной ф используют и коэффициент пористости к _р = ф /(1 — ф ). Уровень грунтовых вод будем характеризовать величиной n _g (x,y, t) = H _g (x,y,t) + b _g (x,y), где

H _g (x,y,t) — толщина слоя грунтовых вод над рельефом слабопроницаемых грунтов Ь д ( ^Х ,у).

В общем трехмерном случае для описания динамики грунтовых вод используется математическая модель движения жидкости в пористой среде, которая, в свою очередь, основана на уравнениях механики многофазных сред [5; 13]:

d( a i y i )

dt

+ V ( a _i y _i v _i ) = 0,

d (a ^ Q^ + ^ ( a t Q i V i ® V i ) = —a i V p i + а ^ у ^ д + V F ij + a i P i Av i ,       (5)

dt

з где а — объемное содержание г-й фазы с плотностью yi и давлением pi; g = {0, 0, —д} —

Pi vj — Vi вектор ускорения силы тяжести; Fij = ai —         сила межфазного взаимодействия между г-й и j-й фазой; р — динамическая вязкость г-компоненты среды; I — характерный размер области г-й фазы, который для пористой среды соответствует характерному размеру пор; вг — некоторый коэффициент, смысл которого выяснится ниже.

Если ограничиться рассмотрением модели многофазной среды, состоящей из двух компонент г = 1 — жидкость (вода) и г = 2 — неподвижный недеформируемый пористый скелет грунта, то v 1 = v, v ₂ = 0, а 1 = ф , а ₂ = 1 — а 1 = Y s , У 1 = у, Р 1 = Р, Р- 1 = Р- , 1 1 = I, в 1 = в - Тогда для такой двухкомпонентной среды из системы (4)-(5) можно получить уравнения, описывающие динамику жидкости в пористой среде:

^7^ + V ( ф уv) = 0,                         (6)

^^f^ + V ( Ф Уv ® v) = —Ф^ Р + Ф уд — ф"^ V + Фp Av. д t                                              в I

В пределе Ф ^ 1 из (7) получаем стандартное уравнение движения в приближении однокомпонентной гидродинамики, так как в этом случае размер пор I ^ то .

Поскольку для фильтрационных потоков в пористых грунтах характерная скорость течения мала ( | v | ∼ 0.01–1 м/сут), то в уравнении (7) можно пренебречь левой частью по сравнению с правой. Кроме того, из-за малости характерного размера пор I можно также пренебречь и последним членом в правой части (7) по сравнению с силой межфазного взаимодействия. С учетом этих предположений из уравнения (7) получим выражение для скорости жидкости в пористой среде:

в 1

v = —р ( v p — уд).

По определению скорость фильтрации u _g связана со скоростью жидкости (скоростью частиц жидкости) в пористой среде v следующим соотношением: u _g = ф v. Учитывая эту связь и выражение (8), для скорости фильтрации будем иметь:

u g =

-

к

( V p ^— уд), ^µ

где к = фв1 = _ — коэффициент проницаемости, зависящий только от свойств ед пористого скелета, а кф — коэффициент фильтрации, который определяется экспериментально. Соотношение (9) — хорошо известный закон Дарси, связывающий скорость фильтрации жидкости через пористую среду с напором или градиентом давления.

Таким образом, если определить скорость жидкости в уравнении непрерывности (6) с учетом (8) и (9), то получим уравнение диффузионного (параболического) типа относительно плотности у:

^д ( ф у)      Г^к ф

— = ^- ( V^{p - e g)}J.

В общем случае коэффициент фильтрации является функцией пространственных координат к ф = к ф (х,у, г), а для замыкания уравнения (10) используется уравнение состояния р = р(у).

Так как на практике при построении границ зон затопления и подтопления в окрестности населенных пунктов характерные пространственные и временные масштабы задачи в горизонтальном направлении существенно больше соответствующих масштабов вдоль вертикальной координаты, то для описания динамики поверхностных и грунтовых вод можно воспользоваться приближением мелкой воды (тонкого слоя жидкости). Проводя процедуру усреднения уравнения (10) по г-координате, аналогичную случаю поверхностных вод, то есть интегрируя (10) по г в пределах от Ь _д до п _д = Н _д + Ь _д в предположении гидростатического равновесия тонкого слоя грунтовых вод р(г) = ед( п _д — г), получим следующее уравнение:

. дНд ^ф "эТ

= V _± (к ф Н д V ± П д )+ д д ,

которое описывает эволюцию толщины Н _д тонкого слоя жидкости в грунте за счет медленных фильтрационных течений (по закону Дарси), определяемых коэффициентом к ф , и действующих в слое грунта источников/стоков воды д _д = д д⁵) + q ^(m?) — q^ ¹? ) — q^ X где величины д^(гп? ) и д д⁵) определяют скорость притока жидкости с поверхности и за счет подземных источников, соответственно, а дд^гп? ) и д^^ — скорость оттока воды из пористого слоя за счет инфильтрации в слабопроницаемый глубинный слой грунта и высачивания на поверхность (подъема грунтовых вод), соответственно.

В пределе однородных грунтов (к ф , ф = const) и плоского дна водоупора (Ь _д = = const) уравнение (11) сводится к уравнению Буссинеска, описывающему безнапорное движение подземных вод со свободной поверхностью (см., например, [6; 19]), а аналитические решения этого уравнения, получаемые после процедуры его линеаризации, используются в методиках определения нестационарных уровней грунтовых вод в окрестности водных объектов при повышении или спаде уровня поверхностных вод (см., например, [18]). После линеаризации нелинейное уравнение Буссинеска переходит в уравнение, являющееся аналогом уравнения теплопроводности Фурье:

эи

1н

a A ^ U + ^ , ψ

где a = к ф Н ₅ / ф , А ^ — дифференциальный оператор лапласиан в плоскости, перпендикулярной оси Ог; U = Н _д Н ₅ при первом способе линеаризации, а при втором —

U = H^/2; Hs = в (Timin + Hmax)/2 — средняя глубина потока грунтовых вод; в — коэффициент, который зависит от отношения Hmin/Hmax и способа линеаризации (см., например, [19, с. 45]); Hmin и Hmax — минимальная и максимальная глубина потока, соответственно.

Аналитические формулы, являющиеся решением уравнения (12) и используемые в методиках расчета нестационарных границ зон подтопления местности грунтовыми водами, сильно зависят как от геометрии задачи, так и от начальных и граничных условий. Например, для плоскопараллельного течения с начальным (бытовым) уровнем грунтовых вод H _g (x,t = 0) = H _min и граничными условиями вида H _g (х = 0,t) = H _max , lim ^g = 0 решение (12) имеет вид: ж >^ Ух

∞

U = U i + (U

-

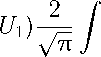
е

- θ ²

d 0 ,

̂︀

где х =      ; U 1 = H _min H _s ; U ₂ = H _max H _s для первого способа линеаризации, а для

2 vat второго — U1 = Hmin/2, U2 = SmaxA

Самосогласованная динамика поверхностных и грунтовых вод определяется параметрами впитывания воды в грунт д ^(т^) и высачивания на поверхность q^ ) , а также гидравлической связью поверхностного и подземного потоков. Различают две основные стадии фильтрационных течений [6; 19]: 1) свободная фильтрация, при которой отсутствует гидравлическая связь между поверхностными и грунтовыми водами; 2) фильтрация с подпором, при которой фильтрационный и грунтовый потоки объединяются и начинают взаимодействовать друг с другом. Свободная фильтрация наблюдается на начальной (первой) стадии промачивания грунтов под водными объектами, а глубина промачивания ξ ограничена снизу фронтом впитывания, который находится выше уровня грунтовых вод n _g . Как только фронт впитывания достигает уровня грунтовых вод, начинается вторая стадия — фильтрация с подпором. Для оценки скорости движения фронта впитывания w( I ) в водопроницаемом слое грунта, подстилающем дно водоема с глубиной H , применяют следующее уравнение [19]:

= d I = к ф ( H + H _k dt    -фу I

+1),

где H _k — высота капиллярного вакуума. Уравнение (14) следует из уравнения (8) на

H + H _k

. Интегрируя уравне-

др  Ар

^-компоненту скорости в предположении, что — ^ —— dz  Az ние (14) при H + Hk = const, можно оценить время т^, за которое фронт промачивания достигнет уровня грунтовых вод, залегающих на глубине Imax = b — ng:

Ч = -ф (H + H k ) [Л — 1п(1 + Л)] , ψ

где Л = I max /(H + H k ).

Как видно из (14), при I ^ 0 скорость впитывания w ^ то , что является следствием линейного приближения, используемого при выводе уравнения (8). В реальных пористых средах за счет нелинейных эффектов и вязкости на глубинах промачивания

^ . Н , скорость впитывания ограничена сверху величиной w _max , которую в рамках простейшей модели можно оценить исходя из того же уравнения (14) следующим образом:

_ кф л,   н \

" ~ _ф²   н,

Свободная фильтрация, в свою очередь, также делится на два типа фильтрационных течений [6; 19] — это так называемые напорная фильтрация и инфильтрация. Если водоем расположен в водопроницаемом грунте, то реализуется случай напорной фильтрации, а при наличии на дне водоема так называемого «экрана», представляющего собой тонкий (покровной) слабопроницаемый слой грунта с коэффициентом фильтрации к _с ^ к ф и толщиной т, возможны оба типа фильтрационных течений в зависимости от соотношения скоростей фильтрации в этих слоях. С учетом (14) и соотношения между скоростью фильтрации и скоростью жидкости в пористой среде можно получить условия возникновения различных типов фильтрационных течений [19]. В случае к ф /к _с <  Ж происходит напорная фильтрация с полным заполнением пор грунта, а при к ф /к _с >  Ж реализуется инфильтрация с частичным заполнением пор грунта, где Ж = (Н ■ Н , + т)/т.

Учитывая тот факт, что направление фильтрационных течений имеет наряду с основной вертикальной составляющей и горизонтальную, обусловленную как процессом рассеяния жидкости на порах грунта, так и горизонтальным градиентом V ± ^ при напорной фильтрации, а также рассматривая характерные времена процессов t & т ^ , можно ограничиться моделью грунтовых вод со свободной поверхностью (11), в которой величина q^(tn^ ) определяется в зависимости от типа фильтрации.

Для случая напорной фильтрации можно записать:

п(inf) = I -ф^), q I 0,

Н >  0 и П _д < Ь, иначе ,

где значение ξ определяется в каждый момент времени посредством численного интегрирования уравнения (14).

При инфильтрации будем иметь:

п(inf) _ Г кф, q 10,

Н >  0 и п _д <  ь, иначе.

Кроме того, при фильтрации с подпором, то есть на второй стадии, когда уровень грунтовых вод достигает дна водоема ( п _д = Ь), в уравнении (11) вместо величины п _д необходимо использовать f = п _д + Н = п .

Величину q g^inf) определим следующим образом:

qf*^{f )} = {

к * , Н д >  0, 0, Н д <  0,

где к * — коэффициент фильтрации в слабопроницаемом глубинном слое грунта.

Высачивание воды из грунта обратно на поверхность можно учесть посредством вычисления в каждый момент времени величины АН _д = п _д — Ь и корректировки толщины слоя жидкости на поверхности Н ив грунте Н _д . Тогда для величины q g“^p) получим:

q^ = ■

ф АН д

τ

0 ,

АН д >  0,

АН д <  0,

где τ — временной шаг в численной модели.

2.    Численная схема и программная реализация

Для численного моделирования самосогласованной динамики поверхностных и грунтовых вод использовались CSPH-TVD-метод [15; 21] и параллельный код («CUDA-DSW»), подробно описанный в работах [24; 26] и являющийся базовой версией вычислительного модуля программного комплекса «EcoGIS-Simulation», который был дополнен модулем расчета фильтрационных течений в слое грунта («CUDA-DGW»).

2.1.    Численный алгоритм

Для численной аппроксимации уравнения (11) проведем стандартную процедуру дискретизации на пространственно-временной сетке (х,у, t) ^ ( х _: ,у з ,t _n ) (x _i+1 = x _: + + h, y j ₊₁ = X j + h, t _{n +1} = t _n + т „ , где h — размер ячеек пространственной сетки, т _п — временной шаг), заменив непрерывные функции их значениями в узлах этой сетки / (x,y,t) ^ / " , а их производные — конечно-разностными аналогами. В результате для уравнения (11) с учетом (17) и (19) получим явную консервативную численную схему второго порядка точности по пространственной координате ~ O(h ² ):

-

И"+1 = //"  ■ -2"— gi’3       gi,j + h2^i,j

[ кф i+1/2,j H gi+1/2,j ⁽ⁿ "i₊1,j - ⁿ "i,j ) -

^к ф i-1/2,3^Hgi-1/2,j ⁽ⁿ "i,j ^—

ⁿ gi — 1, j ) ^{+ к} Ф i,j+1/2 ^H gi,j+1/2 ^{( n} gi,j+1

fl "

"      "     "         gM кфi,3 — 1/2Hgi,3 — 1/2v\gij    ngi,j-1) + T" ,

V i,j

-ri"- ■) ⁿ gi,3

—

где значения функций с дробными пространственными индексами (г ± 1/2, j ± 1/2)

^/ i(j)±1 + / г(3) 2

определяются на границах ячеек как / _i(j) ± ₁/₂ =

Отметим, что представленная численная схема (20) имеет первый порядок точности по времени ~ О( т ), но допускают повышение порядка либо за счет применения явно-

неявного алгоритма Кранка — Никольсона [23], либо при использовании процедуры предиктор – корректор (так называемый алгоритм leapfrog) как в CSPH-TVD-методе [21; 27]. Кроме того, для повышения порядка аппроксимации как по времени, так и по пространственным координатам можно использовать численные схемы высокого порядка точности (см., например, [8; 14]).

В общем случае условие устойчивости численного алгоритма для моделирования самосогласованной динамики поверхностных и грунтовых вод можно представить в виде:

Т " = К min Т^ "" , , T "^grant)) ,

где 0 < К <  1 — число Куранта; т^ ^^"")

hh min       ,                 — величи-

:,з    2 | u "j | , | u "j | + V gH"₃

на временного шага в CSPH-TVD-методе при моделировании динамики поверхностных

вод (см. [21;27]); т^^

min ⁱ,^j

h ² ^ i,j

9^, . И". Ф i,3 gi,3

)

— характерное диффузионное время в

численной модели динамики грунтовых вод (20).

2.2.    Параллельный вычислительный модуль

При разработке расчетного модуля с рабочим названием «EcoGIS-Simulation», предназначенного для моделирования самосогласованной динамики поверхностных и грунтовых вод («CUDA-DSW> + «CUDA-DGW»), использовалась технология параллельных вычислений CUDA для графических процессоров (GPU). Кроме того, при проведении расчетов на компьютерных платформах с несколькими GPU применялась технология GPUdirect (обмен данными между GPU напрямую по шине PCI-E или NVLINK) совместно с технологией параллельных вычислений OpenMP для систем с общей памятью на центральных процессорах (CPU). Реализация расчетного модуля «EcoGIS-Simulation» на основе гибридных параллельных технологий CUDA-GPUdirect-OpenMP позволяет эффективно использовать компьютерные платформы с несколькими CPU и GPU (пх x CPU+m x GPU) и повысить производительность вычислений в тысячи раз по сравнению с последовательной версией на CPU.

В качестве языка программирования был выбран CUDA C [2], являющийся расширением языка C для программирования графических процессоров. На рисунке 1 показана структура вычислительного модуля «EcoGIS-Simulation» в виде потоковой диаграммы, демонстрирующей последовательность выполнения следующих CUDA-модулей:

• •    «DSW» — вычисление временного шага (21) и расчет динамики поверхностных вод (1)–(3) на основе CSPH-TVD-метода, подробное описание численного алгоритма представлено в работах [24; 26];

• •    «DGW» — расчет динамики грунтовых вод (11)–(19) на основе численного алгоритма (20).

3.    Результаты численного моделирования 3.1.    Одномерные расчеты плоскопараллельных течений грунтовых вод

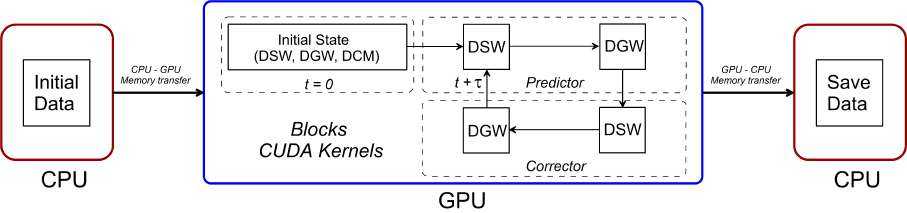
Рис. 1. Потоковая диаграмма для расчетного модуля «EcoGIS-Simulation». Показаны последовательность выполнения блоков CUDA-ядер на GPU и потоки данных между CPU и GPU

Как видно из рисунка 1, для повышения порядка аппроксимации используется метод предиктор – корректор («leapfrog»), подробно описанный для численной схемы CSPH-TVD в работах [21; 27].

Величины b, bg, Н, Нд, п, Пд и пространственные координаты (х,у) будем измерять в метрах (м), а время t в сутках (сут). Для водопроницаемого слоя грунта (песка) примем следующие значения коэффициента фильтрации и пористости: кф = 5 м/сут, ф = 0,4. Будем считать, что слабопроницаемый глубинный слой грунта (водоупор) не пропускает воду, то есть к* = 0.

Рассмотрим сначала задачу о динамике грунтовых вод в одномерном приближении с расчетной областью ж G [0, L] (L = 100 м) и количеством расчетных ячеек N _x = 1000. Построим численные решения уравнения (11) на основе численной схемы (20) с применением алгоритма предиктор – корректор для двух тестовых задач с различными начальными и граничными условиями:

Тест 1

Н д (ж, 0) = 0, Н д (0,f) = H max = 2, Н д (L, 0) = Н тп = 0.          (22)

Тест 2

Н д (ж, 0) = H min = 1, Н д (0, t) = H max = 2, Н д (L, 0) = H min = 1.      (23)

На рисунке 2 представлены пространственные распределения величины пд(ж, t) = = Нд(ж,t)+Ьд (Ьд = —1) в различные моменты времени. Полученные численные решения соответствуют двум видам автомодельных решений нелинейного уравнения в частных производных параболического типа (нелинейного уравнения теплопроводности или диффузии) [7; 9], так как в уравнении (11) коэффициент кфНд перед градиентом уровня грунтовых вод приводит к появлению квадратичной нелинейности (~ Н^) и является аналогом коэффициента теплопроводности as ~ Т (где Т — температура). Для начальных и краевых условий (22) получаем решение в виде нелинейной «тепловой» волны (волны подтопления), распространяющейся в пустоте (по сухому водоупору) и имеющей характерный приблизительно параболический профиль с отличной от нуля производной дпд/дС на фронте волны при Нд(Zo) = 0, где С = ж — Vft — автомодельная переменная, а Vf — скорость фронта волны. В случае (23) имеем существенно более гладкий приблизительно экспоненциальный профиль пд(ж,t) в окрестности фронта волны (Zo) с 1 дпд             , тт , х lim —- = 0 и lim Нд(Z) = Нтп > 0. Как видно из рисунка 2, скорость распростра-с-Со дZ           z -zo нения волны подтопления (повышения уровня грунтовых вод) в задаче Тест 2 почти в два раза превышает аналогичную скорость для задачи Тест 1.

Отметим, что сравнение численных решений Тест 1 и Тест 2 с точными автомодельными решениями уравнения (11) (см., например, [7; 9]) показывает, что разработанный численный алгоритм моделирования динамики грунтовых вод имеет ожидаемый второй порядок точности ~ О( т ² ,^ ² ), а для представленных в работе расчетов относительная погрешность составляет ~ 10 - 4 -10 ^{- 5} .

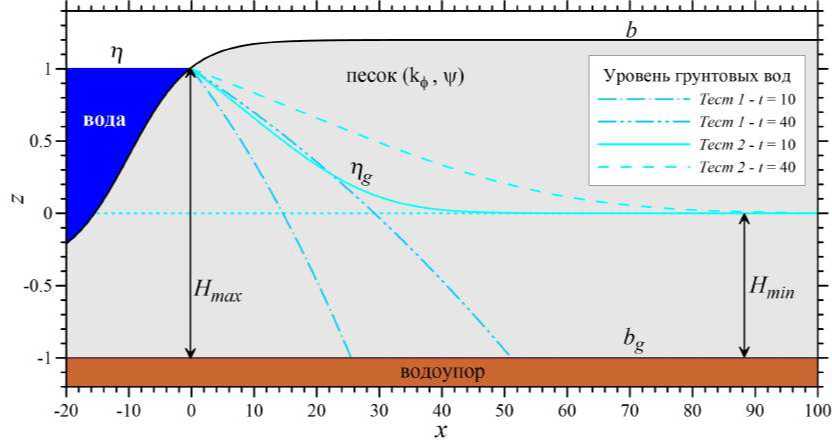
Рис. 2. Динамика грунтовых вод в одномерной (плоскопараллельной) модели (11) при заданных начальных и граничных условиях: (22) — Тест 1 ; (23) — Тест 2

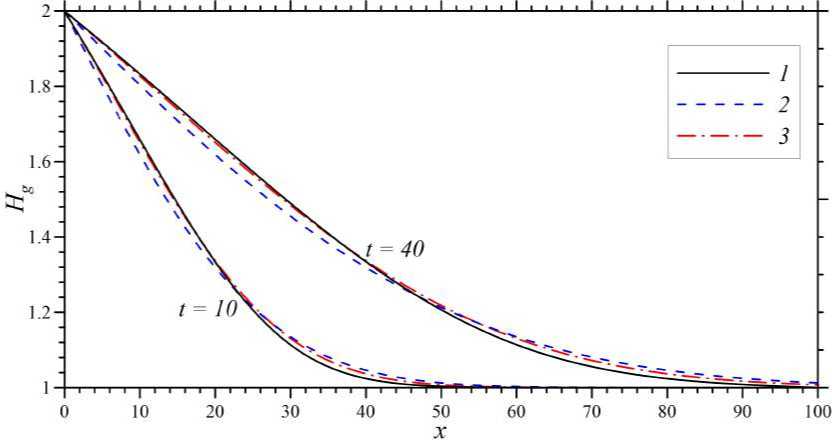
Рис. 3. Пространственное распределение глубины грунтовых вод ( Тест 2 ) в различные моменты времени. Сплошной линией 1 показаны численные решения уравнения (11), штриховой линией 2 — аналитическое решение (13) при первом способе линеаризации (см. уравнение (12)), а пунктирной линией 3 — аналитическое решение (13) при втором способе линеаризации

3.2.    Двумерные расчеты совместной динамики поверхностных и грунтовых вод

Теперь рассмотрим задачу о самосогласованной динамике поверхностных и грунтовых вод на модельном рельефе Тест 3 , решая совместно уравнения (1)–(2) и (11) на двумерной расчетной сетке с х, у Е [ — L/2,L/2] и количеством расчетных ячеек N х N _y = 1024 х 1024. Модельный рельеф поверхности суши и водоупорного слоя грунта зададим в виде функций:

Ь(г) = — 2 cos ^Пг+ + 2.5 + 0.5exp( — г ² /80),   b _g (г) = —,             (24)

50                                   60

где г = Vх² + у ² — расстояние от оси симметрии, измеряемое в метрах (м).

Результаты численного моделирования самосогласованной динамики поверхностных и грунтовых вод представлены на рисунке 4. В начальный момент времени (t = 0) параболический колодец в центре расчетной области наполнен водой, а в грунте (песке) заданы два типа начальных условий: 1) сухой водоупор Н _д (x,t = 0) = 0; 2) постоянный уровень грунтовых вод n _g (х, t = 0) = 0.4 м. Уровень воды в колодце п (х, 0) =4 м, а максимальная глубина 3 м. Параметры грунта такие же, как и в тестовых расчетах ( Тест 1 и Тест 2 ). В качестве модели впитывания поверхностных вод в грунт выбран режим инфильтрации (17).

На рисунке 4 хорошо видны процессы инфильтрации воды с поверхности в грунт, фильтрационные течения в грунте и высачивание воды из грунта обратно на поверхность. В процессе начальной стадии (0 < t . 1) инфильтрации воды происходит понижение уровня поверхностных вод и повышение уровня грунтовых вод в центре расчетной области (под колодцем), а также формируется нелинейная волна подтопления с профилем, подобным случаю Тест 1 (рис. 4a) и Тест 2 (рис. 4b), распространяющаяся в радиальном направлении от оси симметрии. На втором этапе (1 . t . 10) уровни поверхностных и грунтовых вод сравниваются, в дальнейшем происходит совместное понижение уровней воды за счет оттока грунтовых вод из центральных областей в процессе распространения волны подтопления. Третья стадия (10 . t . 100) характеризуется полным осушением колодца и процессом высачивания воды из грунта обратно на поверхность (подъема грунтовых вод) в окрестности осесимметричного рва (г ~ 33), окружающего центральный колодец. На заключительной стадии (t > 100) численное решение стремится к стационарному профилю уровня воды n = П _д = const.

Отметим, что из-за кривизны водоупора, цилиндрической геометрии и нестационар-ности уровня поверхностных вод скорость распространения волны подтопления в задаче Тест 3 оказывается меньше, чем в плоскопараллельной постановке Тест 1 и Тест 2 с постоянным значением подпора (H _max ).

Выводы

В заключение сформулируем основные результаты работы и обсудим области их возможного практического применения.

Построенная математическая модель самосогласованной динамики поверхностных и грунтовых вод позволяет рассматривать гидродинамические течения в окрестности водоемов произвольной геометрии с учетом пространственной неоднородности параметров водопроницаемых грунтов, различные стадии и типы фильтрационных течений (свободная, с подпором, напорная и инфильтрация), а также процессы высачивания воды из грунта на поверхность. Модель основана на уравнениях гиперболического типа (уравнениях Сен-Венана), описывающих динамику поверхностных вод в приближении теории мелкой воды, и уравнении параболического типа (уравнении Буссинеска), описывающего нелинейную динамику грунтовых вод со свободной поверхностью. На основе математической модели разработаны численный метод второго порядка точности и параллельный CUDA-алгоритм, реализованный в виде программного комплекса для суперкомпьютеров с GPU.

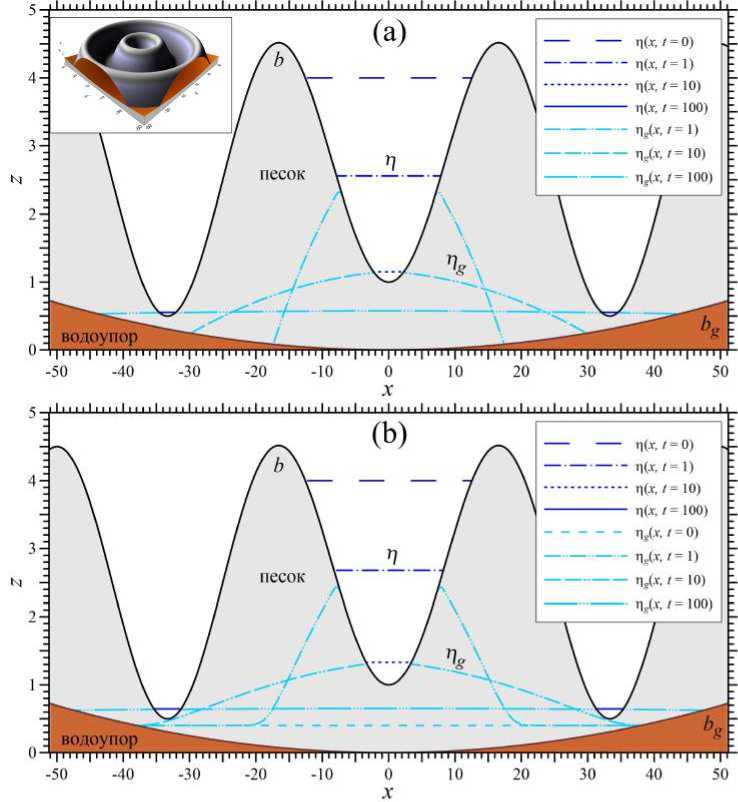
Рис. 4. Самосогласованная динамика поверхностных и грунтовых вод на модельном осесимметричном рельефе для различных начальных состояний:

(a) — сухой водоупор Н _д ( x = 0) = 0; (b) — уровень грунтовых вод п_д(x,t = 0) = 0.4.

На врезке в левом верхнем углу показана 3D модель рельефа

Показано, что аналитические решения линеаризованного уравнения Буссинеска, которые используются в рекомендациях и методиках по расчету границ зон подтопления в окрестности водных объектов в период паводков [6; 18; 19], имеют погрешность в несколько процентов по сравнению с точными решениями даже в самом тривиальном случае плоскопараллельного течения в однородном грунте и требуют подбора коэффициентов модели в зависимости как от структуры начального течения, так и от параметров подпора поверхностными водами. С учетом неоднородности реальных грунтов, существенно более сложной геометрии водных объектов, нестационарности исходных начальных состояний и нелинейных эффектов, возникающих при взаимодействии гидродинамических потоков поверхностных и грунтовых вод, погрешность такого упрощенного линейного подхода может существенно возрасти и привести к некорректным (неадекватным) оценкам уровней грунтовых вод и границ зон подтопления.

Таким образом, методики, основанные на аналитических решениях линеаризованного уравнения Буссинеска в общем случае, то есть для реальной местности с более сложной геометрией водных объектов и пространственной неоднородности параметров подстилающего слоя грунтов, являются существенно менее точными и более затратными по сравнению с предложенной в работе универсальной методикой численного моделировании самосогласованной динамики поверхностных и грунтовых вод. А применение в наших численных моделях высокопроизводительных параллельных вычислений на суперкомпьютерах с GPU позволяет эффективно рассчитывать динамику зон затопления и подтопления на обширных территориях с высоким пространственным разрешением.

Отметим, что для определения точности и пределов применимости рассматриваемой в работе модели самосогласованной динамики поверхностных и грунтовых вод требуется проведение как натурных экспериментов с реальными грунтами, так и модельных численных расчетов на основе полной трехмерной гидродинамики пористых сред.

ПРИМЕЧАНИЕ

• ¹    Работа выполнена при финансовой поддержке Министерства образования и науки РФ (госзадание № 0633-2020-0003).