Численное моделирование силового взаимодействия плитно-свайного фундамента с грунтовым массивом

Сплошные плитно-свайные фундаменты большой площади проектируются под высотные здания, возводимые на слабых грунтах. Учитывая конструктивные особенности плитно-свайного фундамента (фундаментная плита непосредственно взаимодействует как со сваями, так и с грунтовым основанием), предполагается, что часть полной нагрузки, приложенной к фундаментной плите, воспринимается свайным полем, а другая передается непосредственно на грунтовое основание. Одним из важнейших параметров, закладываемых при проектировании такого фундамента, является соотношение величин реакций со стороны грунта, действующих, соответственно, на плиту и сваи. Достоверность этого соотношения определяет качество проектных решений. В настоящий момент расчет таких фундаментов осуществляется в рамках СНиП 2.02.03-85 Свайные фундаменты [1]. Согласно этому нормативному документу, расчет плитно-свайного фундамента может проводиться как для условного абсолютно жесткого штампа на линейно деформируемом полупространстве, либо как плиты на упругом основании с использованием переменного в плане коэффициента упругого сопротивления грунта (в дальнейшем отпора грунта). При этом средняя величина упругого отпора грунта может быть назначена   как непосредственно

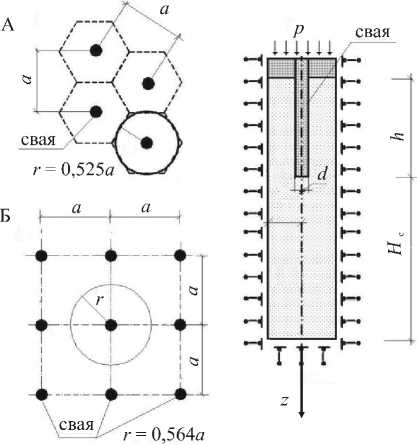
Рис. 1. Расчетная схема метода «ячейки»

из пространственного нелинейного расчета, так и путем решения осесимметричной задачи для ячейки, включающей сваю и окружающий ее массив грунта (Рис. 1, см. [1]. На рисунке 1 показаны две возможные схемы расположения свай (А и Б), где a — шаг свайного поля в окрестности данной сваи, r — радиус рассчитываемой ячейки, H_c — величина сжимаемой (активной) толщи грунтового массива, h — длина сваи, d — характерный размер поперечного сечения сваи, p — внешняя нагрузка на ячейку. При назначении величины коэффициента упругого отпора в краевых зонах и других местах концентрации напряжений учитывается пространственная работа фундаментов. Плановое распределение жесткостных характеристик в этом случае определяется на основании

численного моделирования с использованием геотехнических программ или иных решений, которые, однако, не позволяют с необходимой степенью точности оценивать осадки плитно-свайных фундаментов большой в плане площади, поскольку являются зависимыми от ряда нерешенных проблем, а именно:

• •    методика расчета осадки фундамента на висячих сваях (сваях трения, которые погружаются до сжимаемых грунтов и передают нагрузку на грунт за счет их сопротивления по боковой поверхности и на конце сваи), в рамках которой фундамент условно считается абсолютно жестким штампом на линейно деформируемом полупространстве [1], находит убедительное практическое подтверждение лишь при определении осадки ростверков кустов свай — верхней части свайного или столбчатого фундамента, объединяющей все столбы / сваи в единую конструкцию и имеющей вид ленты или плиты. Эта методика не может быть распространена на расчет осадок плитно-свайных фундаментов больших (в плане) размеров в силу не полной адекватности модели линейно-деформируемого полупространства естественному основанию фундамента;

• •    достоверные оценки осадки одиночной сваи и взаимодействия свай, составляющих куст или поле, могут быть получены только в рамках нелинейных моделей основания, требующих дальнейшего развития и совершенствования;

• •    при исследовании совместной работы системы «здание – фундаментная плита – свайное основание» в упруго-пластической постановке не только резко возрастает время счета, но и возникают достаточно серьезные проблемы со сходимостью и устойчивостью решения дискретной схемы с большим числом степеней свободы.

В данной работе предлагается подход к расчету плитно-свайного фундамента, который позволяет исключить некоторые обозначенные проблемы и априорно с достаточной степенью точности оценить эффективность конкретного плитно-свайного фундамента. Делается допущение, что характерное расстояние между сваями осями свай составляет не более четырех линейных размеров поперечного сечения сваи. Это ограничение сверху на расстояние между сваями обеспечивает их взаимовлияние и совместную работу в едином массиве.

В рамках применяемого подхода система «фундаментная плита – сваи – массив грунта, прорезанный сваями» представляется в виде двух совместно работающих плит — собственно фундаментной плиты ( 1 ) (Рис. 2) и лежащей под ней плиты толщиной l ( 2 ) c эффективными свойствами, определяемыми взаимодействием свай с грунтом. Полагается, что верхняя плита под действием равномерно распределенной вдоль оси y нагрузки P испытывает реакцию грунта интенсивностью P _пл , равную силе взаимодействия плит 1 и 2 , а нижняя плита — реакцию грунта интенсивностью P _св , равную силе взаимодействия плиты 2 с грунтом.

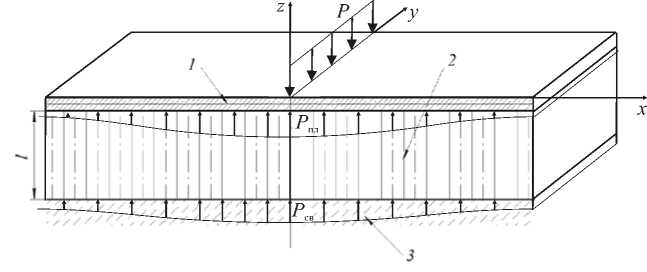
Рис. 2. Расчетная схема – две параллельно лежащие плиты на грунтовом основании: железобетонная фундаментная плита 1 и плита 2 с эффективными свойствами, определяемыми взаимодействием свай с грунтом 3 .

Рассмотрим совместную деформацию двух последовательных слоев, лежащих на упругом двухпараметрическом основании, то есть основании, характеризуемом двумя коэффициентами постели: C ₁ — коэффициентом сжатия, измеряемым в Н/м³ и C ₂ — коэффициентом сдвига, измеряемым в Н/м [2]. Верхний слой — железобетонная фундаментная плита с параметром нагрузки P _пл , нижний слой — массив с неполной системой связей, работающий только на сдвиг, с параметром нагрузки P _св . При этом D — цилиндрическая жесткость фундаментной плиты; G ₀ — модуль сдвига слоя, прорезаемого сваями; C ₁, C ₂ — коэффициенты постели двухпараметрического основания для слоя, на который опираются сваи [2]. Плиты подвергаются действию совпадающих с точностью до параметра систем нагрузок.

Предполагаем, что при соблюдении вышеуказанного условия нагружения отношение P _пл / P св не зависит от конкретного вида нагрузки. Для определения вида этого отношения последовательно решим задачи изгиба двух плит бесконечных размеров, лежащих на упругом основании, при действии равномерно распределенных в направлении оси y нагрузок интенсивностями P _пл и P _св , соответственно.

Решение этих задач может быть получено на основе решения задачи деформирования бесконечной балки на упругом основании от действия распределенной нагрузки q ₀. Оно имеет вид [3]:

w = - СЬ [ M 0 ^{РП 2 ( в} x ) ⁺ ^ о П з ^{( в} x ) ] ⁺ qb ’

< Ф = 2b [M02РПз(Рx) + QoHi(Px)], M = -EJzW" = Mо^фx) + Q П4(рx), _ Q = - EJzW” = - M о 2вП4 (в x) + Q0П2 (в x), где M, Q — внутренние усилия в балке; С — коэффициент постели упругого основания; EJ — изгибная жесткость балки; в — коэффициент, зависящий от относительной величины жесткости основания на просадку Cb и изгибной жесткости балки EJ; ф — угол поворота балки (ф = w'); Q0 — поперечная сила в начальном сечении; M0 — момент в начальном сечении; п,- (вx) (i = 1,2,3,4) — частные решения этой задачи:

П 1 = e ^в x (cos в x + sin в x ), П ₂ = e ^в x (cos в x - sin в x ), П з = e -^ cos в x , П ₄ = e ^в x sin в x .

На основе соотношений (1), (2) получена величина прогиба железобетонной плиты 1 при x = 0 :

0    2 C , где в = 4Ci/(4D) .

Для определения осадки слоя 2 , прорезаемого сваями и сопротивляющегося только сдвигу (условия, обеспечивающие возможность такого деформирования, предполагаются выполненными), запишем уравнение равновесия элемента этого слоя единичной длины. Имеет место следующая цепочка уравнений:

dw = Q ^ d ² w = d I Q |^ P dx   G ₀ ■ l    dx ²     dx ( G ₀ ■ l J       G ₀ ■ l

C 1 ■ w - q G 0 ■ l

^ w" -в2 ■ w =

q

.

G 0 ■ l

Здесь погонные перерезывающие силы Q в слое связаны с прогибом w и интенсивностью заданной распределенной нагрузки q соотношением Q = Q ₀ + C 1 ■ w ■ x - q ■ x , и в 2 = CJ(G ₀ ■ l ).

Решая уравнение (4) в предположении ограниченности прогибов на бесконечности при q = 0 и краевом условии Q ₀ | x 0 = - Р св /2, находим величину прогиба плиты 2 в сечении x = 0 :

0    2 V Ci ■ G0 ■ l ’ где G0 — модуль сдвиговой деформации грунта. Предполагаем, что свойства упругих оснований фундаментной плиты и свайного поля идентичны и характеризуются одним и тем же коэффициентом постели C1 [2]. Приравнивая формулы (3) и (5), получаем р™ = Г^Рс? Рсв V(G0 ■ l)2.

Если свойства оснований, на которые опираются слои, различны и описываются разными коэффициентами постели C ₁ ^п _I P _л^ив и С _1св, то отношение интенсивности нагрузок принимает вид:

P = 4 4D ( ^С Я* I P CB ⁽ ( G o l ^{) 2} C 2 B

Введение для основания фундаментной плиты приведенного коэффициента постели ( C ₁^п_п^р_л^ив ) позволяет учесть взаимодействие (через сваи) жестко скрепленной со сваями плиты с основанием свайного поля. Таким образом, зная долю полной нагрузки, воспринимаемой фундаментной плитой, величины осадок фундамента можно определить, решая задачу изгиба заданной железобетонной фундаментной плиты на упругом двухпараметрическом основании с характеристиками слоя грунта, на который опирается плита под действием нагрузки, создаваемой сооружением [4].

Для проверки полученных отношений распределения полной нагрузки между фундаментной плитой и слоем со сваями в плитно-свайном фундаменте была проведена серия численных экспериментов для двух вариантов свойств грунтового основания под свайным полем. В качестве вычислительного инструмента использован конечно-элементный программный комплекс ANSYS v. 12.1.

В расчетных моделях фундаментная плита, лежащая на свайном поле имела размеры в плане 36,6 x 42 м и толщину 0,6 м. Расстояние между центрами свай принималось равным четырем свайным диаметрам (из условия работы свайного поля в едином массиве), диаметр свай (или поперечный размер) — 0,3 м, длина свай — 12 м. Грунтовый массив представлялся объемными 8-узловыми элементами, каждый узел которых имел три степени свободы: поступательное смещение в направлении x , y и z осей узловой системы координат. Железобетонная фундаментная плита разбивалась на оболочечные 4-узловые элементы, каждый узел которых характеризовался шестью степенями свободы: поступательным смещением в направлении x , y и z осей узловой системы координат, и вращением вокруг осей x , y и z . Свайное поле моделировалось стержневыми 2-узловыми элементами, каждый узел которых обладал шестью степенями свободы: поступательным смещением в направлении x , y и z осей узловой системы координат, и вращением вокруг осей x , y и z . Общее число степеней свободы в расчетной модели составляло порядка 150 000. Модуль упругости железобетонной фундаментной плиты и свай считался равным E б = 31 ГПа, коэффициент Пуассона — v₆ = 0,22.

Рассматривалось два варианта упругого грунтового основания:

– 1-й вариант: грунтовый массив представлялся слоями с одинаковыми деформационными характеристиками, модуль упругости которых равнялся 40 МПа, коэффициент Пуассона — 0,3. Основание имело коэффициенты постели, вычисленные по методике [2] — С 1 = 23852,2 кН/м³ и С ₂ = 2637 кН/м. Мощность грунтового массива под острием, в соответствии со СНиП 2.02.01-83 [5], составляла 13,3 м.

– 2 вариант: грунтовый массив состоял из двух слоев, у первого из которых мощность соответствовала длине свай — 12 м; мощность Рис. 3. Общий вид расчетных моделей      второго слоя — 13,3 м. Физико-механические характеристики слоев были следующими: E1 = 40 МПа; V1 = 0,3 ; E2 = 120 МПа; v2 = 0,3 ; соответствующие коэффициенты постели [2] равнялись С1 = 69783,8 кН/м3 и С2 = 7279,5 кН/м. Суммарная нагрузка на фундаментную плиту в первом варианте расчета составляла 453,6 МПа, во втором — 907,2 МПа.

Для обоих вариантов грунтового основания получены картины распределения осадок фундаментной плиты на сваях под действием равномерно распределенных нагрузок на плиту. Далее в соответствии с формулами (4), (5) получены доли нагрузок, воспринимаемых плитой и сваями для обоих вариантов основания. В 1-м варианте плита воспринимает 51,6% общей нагрузки на фундамент, свайное поле, соответственно, — 48,4%. Во 2-м варианте плита воспринимает 28%, свайное поле — 72%. Также проводился расчет без учета свайного поля, со сниженной общей нагрузкой на фундамент в соответствии с перераспределением, полученным в первой фазе расчетов.

На рисунке 4 показаны картины распределения осадок фундаментной плиты и грунтового массива (изополя) в случае 1-го варианта основания. Максимальная осадка фундаментной плиты c учетом свайного поля и полной доли нагрузки составила U 1 z max = - 0,066333 м (Рис. 4, а ), максимальная осадка фундаментной плиты без учета свайного поля и со сниженной долей нагрузки — U ₂ z max = - 0,067245 м (Рис. 4, б).

На рисунке 5 приведены картины распределения осадок фундаментной плиты и грунтового массива (изополя) в случае 2-го варианта грунтового массива. Максимальная осадка фундаментной плиты c учетом свайного поля и полной доли нагрузки составила U 1 z max =- 0,052385 м (Рис. 5, а ), максимальная осадка фундаментной плиты без учета свайного поля и со сниженной долей нагрузки — U ₂ z max = - 0,052621 м (Рис. 5, б ).

а

U z

б

U z

-0,066333 -0,051172 -0,036012 -0,020851 -0,00569

-0,067245 -0,051989 -0,036734 -0,021479 -0,006224

Рис. 4. Изополя вертикальных перемещений фундаментной плиты в случае 1-го варианта грунтового массива, [м] с учетом ( а ) и без учета ( б ) свайного поля

U z

-0,052621 -0,040697 -0,0286774 -0,01685 -0,004927

Рис. 5. Изополя вертикальных перемещений фундаментной плиты в случае 2-го варианта грунтового массива, [м] с учетом ( а ) и без учета ( б ) свайного поля

-0,052385 -0,040358 -0,026331 -0,016304 -0,004277

В расчетах для обоих вариантов грунтового основания разница полученных осадок фундаментной плиты не превысила 2%. В том, и другом варианте сохранился тот же характер деформирования фундаментных плит. Полученные результаты численного моделирования поведения плитно-свайного фундамента в описанных постановках говорят в пользу работоспособности предлагаемой модели плитносвайного фундамента как слоистого массива с неполной системой связей.

Использование представленной модели при расчетах напряженно-деформированного состояния комбинированных плитно-свайных фундаментов позволит еще на стадии проектирования оценить эффективность принятых конструктивных решений. Мерой эффективности в такого рода фундаментных конструкциях выступает соотношение нагрузок воспринимаемых плитой и сваями.