Численное моделирование сложного пластического деформирования металлов по плоским и пространственным траекториям произвольной кривизны и кручения

Изучение закономерностей сложного пластического деформирования конструкционных материалов имеет принципиальное значение для развития фундаментальных основ математической теории пластичности. При значительном количестве общего числа экспериментальных работ по исследованию процессов сложного упругопластического деформирования металлов и их сплавов большинство экспериментов выполнено на многозвенных ломаных и плоских криволинейных траекториях постоянной кривизны [1–6]. Экспериментов для сложных траекторий, включая плоские и пространственные траектории деформирования произвольной кривизны и кручения, выполнено значительно меньше [5–7]. В то же время для проверки физической достоверности определяющих соотношений теории пластичности

необходимо проведение расчетов и сопоставление полученных численных результатов с имеющимися в литературе экспериментальными данными на широком классе траекторий подобного типа. Результаты таких исследований могут быть также полезны при определении (конкретизации) материальных параметров, скалярных функций и функционалов, входящих в определяющие соотношения термопластичности.

Авторами разработана математическая модель термопластичности [10, 11], описывающая процессы упругопластического деформирования конструкционных материалов (металлов и их сплавов) при сложном нагружении. В настоящей статье дается оценка применимости модели путем сопоставления полученных численных результатов с имеющимися в литературе экспериментальными данными [7] по исследованию закономерностей изменения векторных и скалярных свойств стали 45 на плоских и пространственных траекториях деформирования произвольной кривизны и кручения.

Определение основных характеристик процесса упругопластического деформирования материала (параметров состояния), которые в общем случае описываются тензорами σ _ij , e_ij , e _i ^p _j , ρ _ij и скалярами χ , χ _m , С р и Т , может осуществляться двумя способами [8, 9].

Первый способ заключается в интегрировании определяющих соотношений термопластичности по времени, для чего можно использовать любой из методов решения задачи Коши [8]. Интегрирование — достаточно точный метод нахождения решений обыкновенных дифференциальных уравнений, но при численной реализации краевых задач механики деформируемого твердого тела, например, с помощью метода конечных элементов, возникают сложности из-за значительного увеличения времени вычислительного процесса.

Второй способ [9], при соответствующей формулировке определяющих соотношений и линеаризации алгоритма определения λ , сводится к написанию уравнений термопластичности в приращениях, которые зависят от выбранного шага по времени Δ t . Шаг Δ t может корректироваться при прохождении сложных участков траектории деформирования (например, изломом траектории) или же задаваться постоянным в течение всего расчетного времени при условии выполнения критерия устойчивости вычислений. Этот способ наиболее удобен при решении краевых задач механики деформируемого твердого тела, так как при решении упругопластических задач, в которых параметры процесса деформирования зависят от истории нагружения, отпадает необходимость решения системы дифференциальных уравнений на каждом временном шаге. Именно он и применяется в данной работе.

2.    Сравнение численных результатов с экспериментальными данными

Для более полного экспериментального обоснования и проверки физической достоверности определяющих соотношений теории пластичности необходима постановка экспериментов с максимально широким диапазоном изменения кривизны траектории в пределах одного опыта. Особый интерес представляют опыты по изучению процессов сложной разгрузки материала и связанных с этим закономерностей изменения их скалярных и векторных свойств. Таким образом, постановка экспериментов по сложному активному нагружению и разгрузке материалов на плоских криволинейных, пространственных многозвенных ломаных траекториях и численный анализ этих процессов являются весьма актуальными [5–7].

В работе [7] приведены результаты экспериментальных исследований напряжений σij и деформаций eij (i, j= 1, 2, 3) , а именно, закономерности изменения векторных и скалярных свойств стали 45 на плоских и пространственных траекториях деформирования произвольной кривизны и кручения, которые получены в лаборатории механических испытаний кафедры сопротивления материалов, теории упругости и пластичности Тверского государственного технического университета на автоматизированном расчетно-экспериментальном комплексе СН–ЭВМ под руководством профессора В.Г. Зубчанинова. Эксперименты выполнены на тонкостенных трубчатых цилиндрических образцах с длиной рабочей части l = 110 мм, толщиной стенки h = 1 мм и радиусом срединной поверхности R = 15 мм, изготовленных из стали 45 в состоянии поставки. Образцы нагружались осевой силой Р, внутренним давлением q и крутящим моментом M при нормальной температуре (T — 20°C) по заданной программе испытаний. В испытаниях при растяжении, кручении, нагружении внутренним давлением компоненты тензоров напряжений с0 и деформаций eij (i, j = 1, 2, 3) вычислялись по формулам:

Р о. i =---------,

11 2 п Rh

R

^ 22 = q -г, h

M

° 1² = 2 п R² h ’

A l e^{11 —} l ’

e 22

A R

R ^,

e 12

R

= Ф-- , 2 l

V

CT e — 3K ’

e 33               • ⁽ e ll + e 22 ),

1 - V

где A l — абсолютное удлинение рабочей части образца; A R — изменение радиуса срединной поверхности образца; ф — угол взаимного поворота сечений; К — объемный модуль упругости Эйлера-Юнга; v — коэффициент Пуассона.

Компоненты S_k , Э _k ( i , j = 1, 2, 3) векторов напряжений S и деформаций Э в девиаторном трехмерном изображающем пространстве, связанные соотношениями

S = S k • i k ,     Э = Э к • i k       ( к = 1, 2, 3),

где i_k — единичные векторы базиса А.А. Ильюшина, рассчитывались по формулам:

S 1 =

О

2 (СТ22 + CT33 ) ,

S, = V2 (o' +1 o' 1 = ^22

2             22   211

Я 31

,

12, Э1

^e 11 ^{- e} 0 ) ,

Э, = V2 I e' + - e'

2            22    2 11

2 1 ^e 22 + 2 ^e n    2 ^e

' = V2e' = V2e

3 V ^e 12      * "^ ^e 12 ^.

222     222

модули девиаторов

Здесь S — CTij • CTij — SS1 + S2 + S3 , Э — eje^ • e’j — ЭЭ+ + Э2 + Э3

векторов напряжений и деформаций.

С появлением пластических деформаций наблюдался быстрый рост коэффициента

Пуассона v: vp — 0,5 уже при деформации Э « 1% [7]. При обработке результатов испытаний это позволило использовать условие несжимаемости е —

3 ⁽ е 11 ⁺ е 22

+ е ₃₃ ) — 0.

Кроме того, принималось допущение, что напряженное состояние образцов плоское ^{( CT} 33 ^CT 32 ^CT 31 ⁰ , е 32 е 31 ⁰ , е 33 ^ ⁰ ) ^[7].

Расчетный анализ процессов деформирования лабораторных образцов с использованием записанных соотношений термопластичности [10, 11] проводился при следующих материальных параметрах стали 45: модуль сдвига G = 76920 МПа; модуль объемного сжатия К = 166670 МПа; начальный радиус поверхности текучести С ⁰ _р = 350 МПа; модули анизотропного упрочнения g 1 = 8000 МПа, g 2 = 80 МПа.

При численном моделировании экспериментальные траектории деформаций e_ij ( t ) являлись заданными, а траектории напряжений σ _ij ( t ) находились в результате интегрирования определяющих соотношений термопластичности по заданной истории изменения e_ij («жесткое» нагружение). Полученные численные результаты сопоставлялись с экспериментальными данными, взятыми из работы [7] (см. Рис. 1–9; на всех рисунках сплошная линия соответствует численным результатам, а штриховая — экспериментальным).

В первой серии опытов образец из стали 45 предварительно закручивался до значения Э 3 = 0,0062, а затем на плоскости Э 1 –Э 3 реализовывалась криволинейная траектория постоянной кривизны k 1 = 161,3 и радиуса R = 0,0062 («глобальная» диаграмма деформирования σ _u - e_u , где σ _u , e_u — интенсивности тензоров напряжений и деформаций соответственно, представлена на рисунке 1). След запаздывания, найденный по двухзвенной ломаной линии, составил h = 10^-2. Поэтому данная траектория была отнесена к траекториям большой кривизны, для которых характерно неравенство ( k 1 >  h ^-1) [7].

На рисунке 2 изображен отклик на программу испытаний в пространстве напряжений. В процессе нагружения появлялась компонента деформации Э₂ , которая при выполнении условия несжимаемости должна была равняться нулю [7]. Данное отклонение возможно либо вследствие возникновения деформационной анизотропии, либо вследствие начальной анизотропии по толщине оболочки, появляющейся при ее технологической обработке. Несмотря на то, что Э 2 была существенно меньше Э 1 и Э 3 , траектория деформирования становилась пространственной. В то же время траектория напряжений (Рис. 2) оставалась плоской в силу выполнения условия σ ₃₃ ≈ 0 .

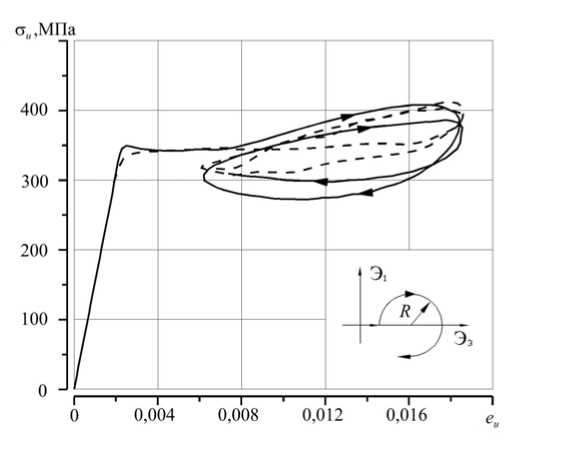
Рис.1. «Глобальная» диаграмма сложного деформирования предварительно закрученного образца из стали 45

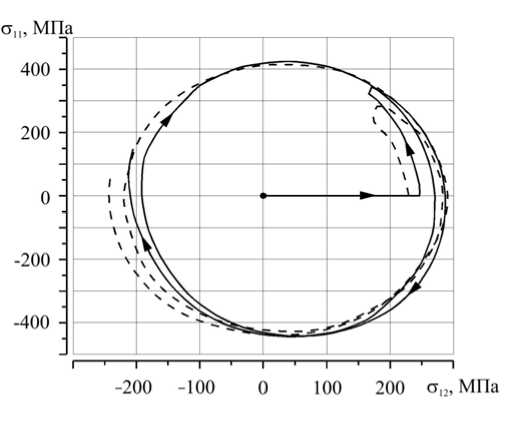
Рис. 2. Траектория напряжений на плоскости Э 1 – Э 3 , соответствующая реализованной плоской замкнутой круговой траектории деформирования ( k ₁ = 161,3 и R = 0,0062)

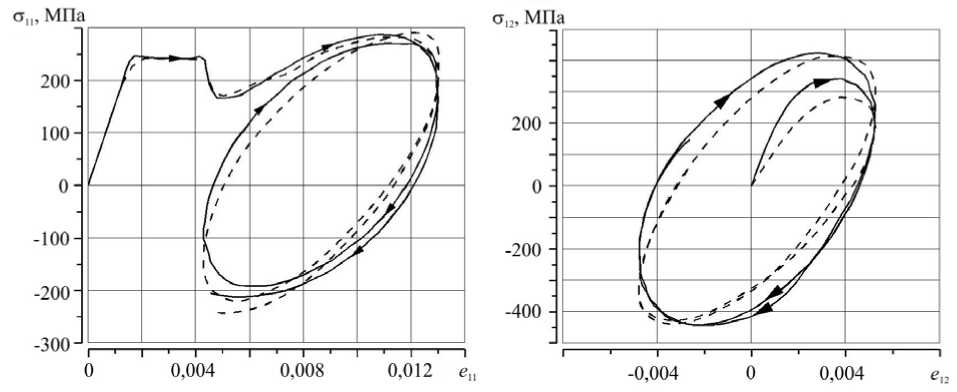
На рисунке 3 представлены «локальные» диаграммы деформирования: а — в координатах с 11 - e 11 ; б — в координатах о ₁₂ - e ₁₂ Рисунки свидетельствуют о качественном и количественном совпадении опытных и расчетных данных.

В следующей серии опытов трубчатые образцы из стали 45 растягивались в пластическую зону до уровня Э 0 = 0,0098 (образец № 1) и Э 0 = 0,0083 (образец № 2), Э 0 = Э 3 = 0, а затем, после излома траекторий на углы а 1 = 90°, а ₂ = arctg ( к 2 / к 1 ) , деформировались по винтовой траектории постоянной кривизны ( k 1 ) и кручения ( k 2 ). Траектория образца № 1 имела большую кривизну ( k 1 = 198,2) и малое кручение ( k 2 = 15,6), траектория образца № 2 — малую кривизну ( k 1 = 37,2) и большое кручение ( к ₂ = 114,2). Начальной точке винтовой траектории соответствовало значение е 11 = 0,008 для образца № 1 и е 11 = 0,0068 для образца № 2, что послужило основанием использовать условие несжимаемости при обработке экспериментальных данных на винтовой части траектории [7].

а                                         б

Рис. 3. Локальные диаграммы деформирования образца из стали 45 в координатах а_п - e 11 ( а ) и

° 12 ^{- e} 12⁽ б )

Данные опытов и их сравнение с полученными численными результатами приведены на рисунках 4–6 (части а рисунков соответствуют образцу № 1, части б — образцу № 2).

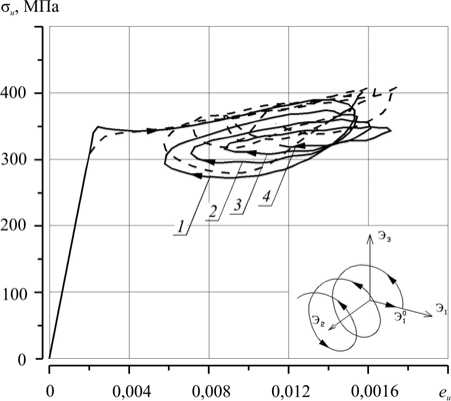
На рисунке 4 представлены «глобальные» диаграммы деформирования σ _u - e_u (реализовано четыре витка траектории, которые отмечены цифрами), а на рисунке 6 — «локальные» диаграммы σ ₁₁ - e ₁₁ и σ ₁₂ - e ₁₂

Рисунок 5 содержит проекции вычисленных траекторий на программу испытаний в пространстве напряжений σ ₁₁ -σ ₁₂ .

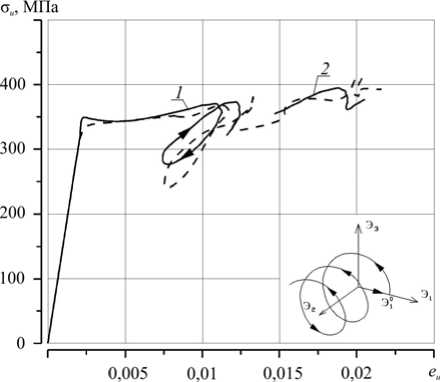
а                                          б

Рис. 4. Диаграммы сложного деформирования образцов № 1 ( а ) и № 2 ( б ); сплошная линия – результаты вычислений; штриховая линия – экспериментальные данные [7].

1 , 2 , 3 , 4 – витки реализованной траектории деформирования

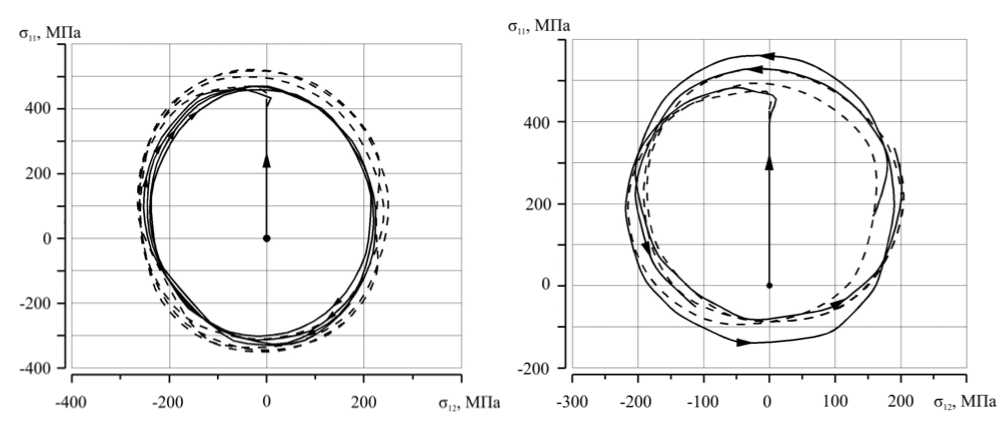
а                                          б

Рис. 5. Траектории напряжений на плоскости σ ₁₁ -σ ₁₂ , соответствующие реализованным пространственным винтовым траекториям деформирования кривизны ( k 1 ) и кручения ( k 2 ): k 1 = 198,2 и k 2 = 15,6 ( а ); k 1 = 37,2 и k 2 = 114,2 ( б )

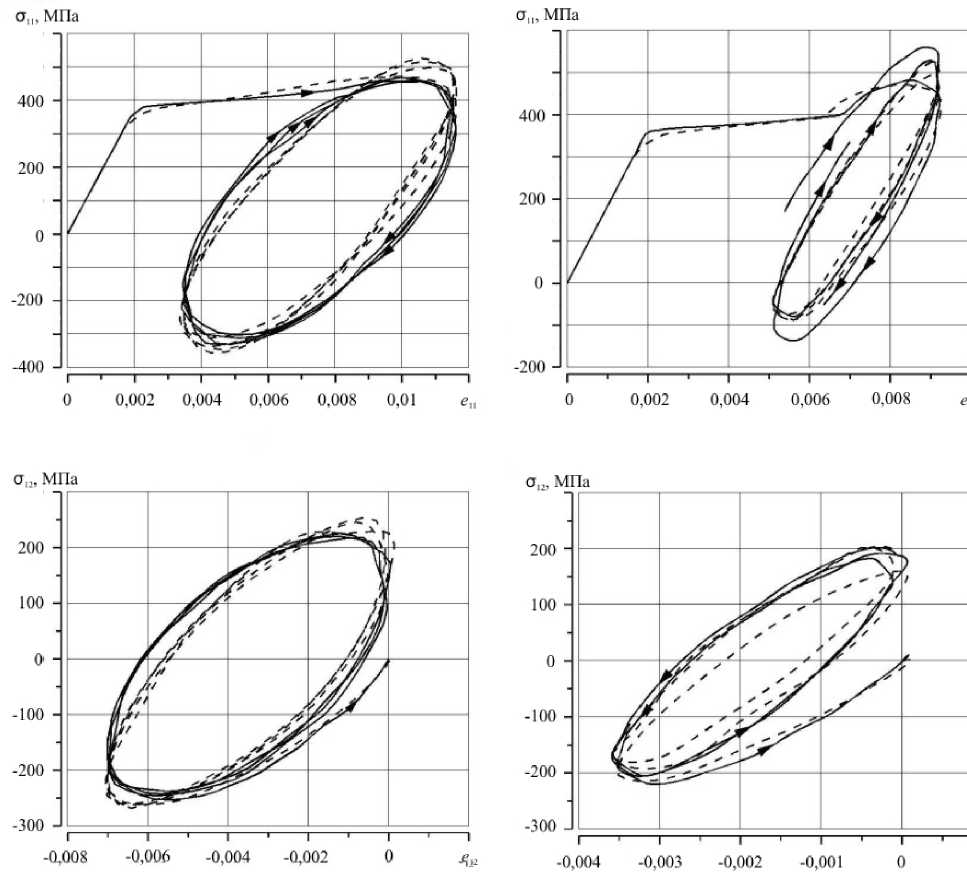
б

а

Рис. 6. Локальные диаграммы деформирования для образцов № 1 ( а ) и № 2 ( б )

В целом, сопоставляя полученные численные результаты с данными экспериментов, можно отметить качественное и количественное совпадение модельных представлений с опытными данными плоского и пространственного деформирования образцов из стали 45 на траекториях произвольной кривизны и кручения. Некоторые отличия расчетных значений от экспериментальных можно объяснить, например, неточностями при задании физико-механических характеристик материала, а также тем, что при обработке экспериментальных данных принималось условие несжимаемости материала.

3.    Заключение

Проведена оценка адекватности определяющих соотношений упругопластичности [10, 11] путем сопоставления результатов численных расчётов с известными из литературы опытными данными для плоских и пространственных траекторий непропорционального деформирования произвольной кривизны и кручения, которая подтвердила правильность моделирования процессов сложного упругопластического деформирования конструкционных материалов (металлов и их сплавов).

Работа выполнена при поддержке Российского фонда фундаментальных исследований (проект № 09-08-00266–а).