Численное моделирование смешанной конвекции в жидком металле при подъемном течении по круглой обогреваемой трубе в условиях поперечного магнитного поля
Автор: Листратов Я.И., Шафиков И.И.
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 4 т.17, 2024 года.
Бесплатный доступ
Рассмотрены процессы гидродинамики и теплообмена при смешанной конвекции жидкого металла (число Прандтля составляет 0.025) в подъемном течении по вертикальной трубе в условиях поперечного магнитного поля. Исследование выполнено с использованием метода прямого численного моделирования. Расчет проводился при числах Рейнольдса до 12000, числах Ричардсона от 0 до 2.4 и числах Гартмана до 550 для двух предельных случаев проводимости стенок трубы. Результаты моделирования для изолированной трубы сравнивались с данными измерений в экспериментах на ртути. Влияние поперечного магнитного поля проявляется в подавлении турбулентного переноса и ламинаризации течения с образованием у продольной скорости сильной неоднородности в профиле по углу и высоких градиентов в поперечном направлении. В зависимости от проводимости стенки трубы и соотношений параметров - числа Ричардсона и Гартмана, возникающие течения с различной топологией профиля продольной скорости обуславливают распределение температуры в стенке и значения коэффициентов теплоотдачи. Показано, что в магнитном поле при изолированной стенке с возрастанием числа Ричардсона течение имеет тенденцию к неустойчивости (к зарождению и обрыву струй, появлению вихревых структур), которая развивается в формирующихся вблизи стенок трубы слоях Робертса, ориентированных перпендикулярно магнитному полю. Периодический процесс генерации и обрыва струй и возникающие вихревые структуры, сохраняются в магнитном поле и вызывают флуктуации компонент скорости и температуры в потоке. Получена зависимость для сопротивления трения на стенке и теплоотдачи (числа Нуссельта) от числа Ричардсона.
Смешанная конвекция, жидкий металл, теплообмен, поперечное магнитное поле
Короткий адрес: https://sciup.org/143183752
IDR: 143183752 | DOI: 10.7242/1999-6691/2024.17.4.37
Текст научной статьи Численное моделирование смешанной конвекции в жидком металле при подъемном течении по круглой обогреваемой трубе в условиях поперечного магнитного поля
Особенности теплообмена в каналах при течении жидкометаллических теплоносителей важны для реальных технических аппаратов. Одними из важнейших приложений, где применение жидких металлов имеет хорошие перспективы, является разработка термоядерного реактора типа токамак ( то роидальной ка меры с ма гнитными к атушками) с магнитным удержанием плазмы, а также ядерные реакторы с жидким металлическим теплоносителем. В таких устройствах течение жидкой металлической электропроводящей жидкости сопровождается сильным воздействием тепловой нагрузки и магнитного поля, что может приводить к значимому влиянию термогравитационной конвекции [1] .
Исследования теплообмена при вязкостно-инерционно-гравитационном течении жидкости в вертикальных трубах в отсутствие магнитного поля ведутся очень давно. Рассматриваются подъемные и опускные потоки, которые в условиях обогрева стенки канала служат причиной развития режимов «смешанной» конвекции. Для неметаллических жидкостей при турбулентном течении, см., например, работы [2] и [3] , получены зависимости коэффициента теплоотдачи от числа плавучести (Bo): при его малых значениях в подъемном течении наблюдается ухудшенный режим теплообмена; с увеличением числа плавучести теплоотдача начинает расти; при опускном течении в условиях неустойчивой стратификации плотности теплоотдача увеличивается с ростом числа плавучести.
Режим ухудшенного теплообмена при подъемном течении связывается с определенным соотношением сил в потоке, при котором в условиях устойчивой стратификации плотности «структурное» воздействие сил плавучести обнаруживается в подавлении турбулентного переноса вблизи стенки, в то время как их «внешнее» влияние, приводящее к М-образным профилям скорости, проявляется слабо [4] . Для жидких металлов вышеописанная тенденция качественно сохраняется, что показано в недавнем обзоре экспериментальных работ [5] , однако наблюдается более сильная зависимость от числа Прандтля, которое у жидких металлов отличается на порядки от аналогичного числа, например, у воды или масла. Исследованиями турбулентной смешанной конвекции натрия в равномерно нагретой вертикальной трубе [6] установлена и противоположная закономерность: теплообмен усиливается при восходящем потоке и ухудшается при опускном. Такое поведение более соответствует закономерностям смешанной конвекции при ламинарном течении.
Смешанная конвекция жидких металлов в условиях поперечного магнитного поля представляет интерес в контексте разработки проектов тестовых модулей бланкета — устройства, защищающего внешнюю среду от излучения плазмы, изнутри повторяющего контур вакуумной камеры термоядерного реактора ITER (International Thermonuclear Experimental Reactor) [7] , предназначенного для демонстрации возможностей коммерческого использования термоядерной реакции синтеза и решения сопутствующих физических и технологических проблем. При этом главными особенностями воздействия магнитного поля является подавление турбулентности и развитие пространственной анизотропии течения, которые напрямую связаны с джоулевой диссипацией
Статья опубликована в открытом доступе по лицензии CC BY 4.0
электрических токов, индуцируемых в потоке металла. Трансформация течения в трубах и каналах под действием магнитного поля зависит от геометрии, электропроводности стенок и управляющих критериев подобия — чисел Рейнольдса, Грасгофа и Гартмана, а также их соотношений — чисел Стюарта и Ричардсона.
Течения в прямоугольных каналах в рассматриваемой конфигурации, под которой понимается взаимные направления векторов магнитного поля, гравитации и вынужденного течения, наиболее исследованы экспериментально и численно [7] . В потоке проводящей жидкости, пересекающем магнитное поле, индуцируются электрические токи, перпендикулярные и потоку, и магнитному полю. Если стенки канала электропроводны, токи замыкаются внутри них, если стенки изолированы, то в прилежащих к ним «гартмановских» слоях. Cила взаимовлияния индуцированных токов и приложенного магнитного поля направлена против течения, при этом может распределяться неоднородно по сечению канала и изменять картину осредненного течения. Трансформация профиля средней скорости при высоких значениях чисел Гартмана (например, порядка 10 4 , характерном для бланкетов термоядерных реакторов) приводит к образованию очень тонких пристенных слоев с чрезвычайно высокими градиентами скорости, что служит причиной возрастания гидравлического сопротивления, а также возможного развития в таких потоках сдвиговых неустойчивостей.
В недавней теоретической работе [8] применительно к условиям бланкета показано, что при подъемном течении основная часть потока движется вблизи обогреваемой стенки в виде струи, в некоторых случаях становящейся неустойчивой, переходящей в крупные вихри масштаба ширины канала, захватывающие горячие объемы жидкости от стенки и генерирующие флуктуации температуры. Такого рода температурные флуктуации, называемые «магнитоконвективными», ранее неоднократно детектировались в экспериментальных работах при других конфигурациях течений в магнитном поле [7] . Они могут представлять проблемы для прочности конструкций бланкетов, так как обладают низкой частотой и высокой амплитудой, которая по величине сопоставима с перепадом температуры «жидкость–стенка».
Течения в трубах в поперечном магнитном поле трансформируются похожим образом, но имеют свои геометрические особенности [9] . Хорошо изучены конфигурации опускных и горизонтальных течений в трубах [7] , для которых уже установлены диапазоны параметров, определяющих режимы течения и условия возникновения магнитоконвективных флуктуаций, а также для этих условий проведены исследования влияния проводимости стенок с учетом загрязнений на их поверхности [10] . Для подъемных течений с однородным обогревом удалось найти лишь одну экспериментальную работу — [11] , в которой с применением микротермопарных зондов в потоке получены профили осредненной скорости и температуры, распределения локальных коэффициентов теплоотдачи, пульсационные характеристики полей температуры. Также обнаружено сильное воздействие плавучести и поперечного магнитного поля на течение и теплообмен, выявлены режимы с возникновением магнитоконвективных флуктуаций температуры в потоке.
В данной работе представлены результаты численного анализа смешанной конвекции в подъемном течении жидкого металла (ртути) по трубе в условиях поперечного магнитного поля с использованием конфигурации и параметров, как физических, так и геометрических, соответствующих работе [11] .
-
2. Метод исследований
-
2.1 Постановка задачи
-
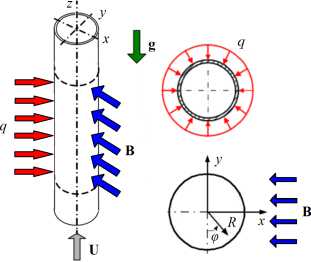
Рассматривается подъемное течение и теплообмен ртути в круглой обогреваемой однородно (q = const, где q — плотность теплового потока) по длине и периметру трубы с внутренним диаметром d= 19 мм, помещенной в зазор электромагнита, создающего постоянное поперечное по отношению к трубе магнитное поле с индукцией B (Рис. 1а ). Геометрия расчетной области с течением жидкости, обогревом и магнитным полем моделируется в приближении к конфигурации экспериментальной работы [11] , при этом стенка трубы во внимание не
( б )
q = const
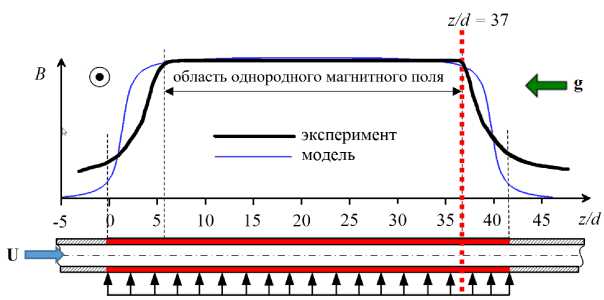
Рис. 1. К постановке задачи: геометрия области ( а ); зона обогрева и распределение индукции магнитного поля ( б )
принимается. Ось z системы координат направлена вдоль оси трубы по потоку, то есть противоположно вектору ускорения свободного падения g . Общая длина рабочего участка составляет L z = 52d, при этом зона однородного обогрева равняется 42d (Рис. 1 б ). Рабочий участок находится в поперечном магнитном поле с основной компонентой, направленной против оси x. Эпюра поперечной компоненты магнитного поля представлена на рисунке 1 б и содержит однородную область длиной 32d. Входная и выходная области электромагнита описываются выражениями дипольного приближения [12] .
Режимные параметры течения выбраны приближенными к экспериментальным исследованиям на ртути [11] . Основным обсуждаемым режимам соответствуют средняя скорость потока U 0 , не превышающая 0.07 м/с, индукция магнитного поля B 0 в однородной области до 1.1 Тл, тепловой поток на стенке q до 75 кВт/м 2 . Теплофизические свойства ртути принимаются постоянными и равными их значениям при средней температуре ртути 25 ºС [13] .
Таблица. Теплофизические свойства ртути
|
Наименование |
Значение |
|
Плотность ρ , кг/м 3 |
1.352 · 10 4 |
|
Кинематическая вязкость ν , м 2 /с |
1.11 · 10 -7 |
|
Теплопроводность λ , Вт/(м · К) |
8.37 |
|
Удельная теплоемкость C p , Дж/(кг · К) |
139.4 |
|
Электрическая проводимость σ , 1/(Ом · м) |
1.039 · 10 6 |
|
Коэффициент термического расширения β , 1/К |
1.82 · 10 -4 |
|
Число Прандтля Pr = А/ (pC p v) |
0.025 |
-
2.2. Физическая модель
Рассматривается нестационарное течение несжимаемой электропроводящей жидкости с постоянными физическими свойствами. Используется квазистатическое приближение магнитной гидродинамики [14] , которое можно применять при условии малости магнитных чисел Рейнольдса Re m = U 0 da^ 0 ^ 1 и Прандтля Pr m = Re m /Re = va^ 0 ^ 1 (^0 — магнитная проницаемость вакуума). Во-первых, внешнее приложенное магнитное поле B много больше, чем возмущения магнитного поля b , вызванные электрическими токами, индуцируемыми в жидкости. Во-вторых, индуцированное поле мгновенно перестраивается при изменении скорости потока. Таким образом, в квазистатическом приближении диффузия магнитного поля преобладает над его адвекцией. Взаимодействие движущейся электропроводящей среды и магнитного поля сводится к одностороннему влиянию магнитного поля на течение. Тогда закон Ома можно записать как j = ^( —V ^ + u х B ), а выражение для электромагнитной (пондеромоторной) силы, соответственно, в виде: F L = j х B . Для замыкания системы уравнений записывается закон Кирхгофа div j = 0 ив итоге следует уравнение Пуассона для электрического потенциала: V 2 ^ = V- ( и х B ).
Для учета термогравитационной конвекции используется приближение Буссинеска [4] , согласно которому переменность плотности жидкости в зависимости от температуры присутствует только в уравнении движения, что приводит к появлению в нем линейного относительно температуры члена, выражающего силу плавучести. При этом и вышеперечисленных допущениях после ввода безразмерного вектора магнитного поля e b = B /B 0 и силы плавучести e g = g /g 0 и пренебрежения вязкой и джоулевой диссипацией в уравнении баланса энтальпии получается 3D система уравнений физической модели течения в безразмерном виде:
— + ( U -V ) U = -V p+Re -1 V 2 U +Ha 2 Re -1 j x e b +Gr q Re - 2 0 e g , (1)
|
V- U = 0, |
(2) |
|
+ ( U •V ) © = (RePr) -1 V 2 0 , ∂t |
(3) |
J = -W+ U х е ь , (4)
V 2 ^ = V- ( U x e b ), (5)
включающая уравнения Навье–Стокса (1) ; уравнение неразрывности (2) ; выражение баланса энтальпии, записанное относительно безразмерной температуры Θ (3) ; закон Ома (4) ; уравнение для потенциала электрического поля (5) . В уравнениях (1) – (5) в качестве масштаба длины для координат x, yи z используется внутренний диаметр рабочего участка трубы d, для скорости — средняя расходная скорость жидкости U 0 , для времени — d/U 0 , для давления — ρU 0 2 , для электрического потенциала — U 0 B 0 d, для плотности тока — σU 0 B 0 , для температуры — qd/λ.
Безразмерными параметрами задачи (1) - (5) являются: число Рейнольдса Re = U 0 d/v, определяющее режим течения жидкости; число Гартмана Ha = B 0 dy/a/(Vp) или число Стюарта N = Ha 2 /Re, выражающее степень влияния магнитного поля на поток; число Грасгофа Gr q = g0ed 4 q/(y 2 А) или число Ричардсона Ri= Gr q /Re 2 , описывающее степень воздействия силы плавучести на поток.
-
2.3. Граничные условия
-
2.4. Численный метод
Задача решалась методом прямого численного моделирования (DNS) с помощью консервативной конечно-разностной схемы 2-го порядка на структурированной совмещенной сетке [16] в цилиндрических координатах (r,ф,z). Точность и эффективность схемы при моделировании течений с высокими числами Гартмана продемонстрирована, например, в [17] . Детали и особенности метода для цилиндрической системы координат изложены в [18] . Моделирование проводилось на сетке с N = N r х N ф х N z = 128 х 256 х 4096 узлами, равномерной по оси z и углу φ . По r сетка сгущалась по направлению к стенкам трубы. Число узлов и параметр сгущения подбирались исходя из результатов предварительных расчетов, выполненных с целью оценки сеточной сходимости, и выбраны способными разрешить масштабы турбулентности в потоке, а также процессы в узких пристеночных «гартмановских» слоях. Шаг по времени составлял 10 - 3 безразмерных конвективных единиц, что существенно ниже «колмогоровского» временного масштаба турбулентности.
-
2.5. Представление результатов
Твердые стенки трубы в расчете не учитывались. Граничные условия на границе «жидкость–твердая стенка» были следующими: для скорости — условия «прилипания»; для температуры — условия второго рода (AdT/dn) | w = q — постоянство положительной плотности теплового потока в зоне обогрева и равенство нулю за ее пределами. Для электрического потенциала условия определялись с физической точки зрения, а именно как безразмерная относительная электропроводность стенки C w = a w 8/(ad), где 8 — ее толщина, а a w — ее электропроводность. При неучете в модели стенок на границе «жидкость–твердая стенка» использовалось два предельных варианта условий. Первый вариант — это электрически изолированные стенки (C w ^ 0), то есть на всех твердых стенках расчетной области задавалось условие равенства нулю нормальной к ним компоненты плотности электрического тока: j n | w = а (д^ /dn) | w = 0. Для течений жидких металлов тонкостенных экспериментальных участках, как правило C w ^ 1, что соответствует этому условию. Второй вариант — это идеально проводящие стенки (C w ^ то ); в этом случае присутствовал постоянный электрический потенциал ^ | w = 0.
На вход расчетной области поступал изотермический поток. Поле скорости на входе представлялось двумя способами. При первом из них на каждом шаге по времени поле скорости выбиралось на основе независимого, заранее рассчитанного распределения скорости в изотермическом турбулентном течении с тем же числом Рейнольдса на участке l = 5d (длиной в 5 калибров) и с периодическими граничными условиями. При втором способе использовался дополнительный изотермический участокрасчетной области длиной L = 25d (в25 калибров) с установленным на его входе хонейкомбом — сотовой гибкой и легкой панелью, что позволило сформировать турбулентное течение. Количество отверстий в хонейкомбе составляло m = 31 и подбиралось с помощью предварительных расчетов, а размещение отверстий подчинялось принципу минимальной площади между ними [15] . На входах всех отверстий хонейкомба для продольной скорости полагались ламинарные параболические профили, которые дополнялись случайными возмущениями с амплитудой ~ 1-2% от средней скорости потока.
На выходе из расчетной области для вектора скорости применялось конвективное условие d U /dt + U 0 d U /dz = 0, а для температуры — дО/dz = 0. Для электрического потенциала на входе и выходе задавались условия второго рода: дФ/dz = 0.
Сопротивление трения рассчитывалось по формуле для безразмерного касательного напряжения на стенке:
_ 1 du z
Т = - Re dR
при R = r/d = 0.5, осредненному по периметру трубы в каждом рассматриваемом сечении с
w
координатой z . Результаты расчетов сравнивались с известной зависимостью Филоненко [19] для турбулентного течения в трубе:
( с =8т о = (1.82lgRe - 1.64) 2 .
В задачах теплообмена обычно вводится среднемассовая температура жидкости T , которая априори определяется из теплового баланса на равномерно обогреваемом участке как T(z) = T | z=0 + 4 q ^ (z/d). В дальнейшем температура в расчетной области отсчитывалась от среднемассовой T(z), таким образом, поле температуры в безразмерном виде представлялось как
T - T (z) qd/A .
Коэффициенты теплоотдачи находились в виде безразмерных чисел Нуссельта:
Nu =
αd
qd
A X(T c - T (z
_ 1 0) = О с ,
где Θ c — средняя по периметру трубы безразмерная температура стенки в каждом рассматриваемом сечении с координатой z.
Для анализа и сравнения результатов расчетов безразмерных чисел Нуссельта далее использовалась эмпирическая зависимость Субботина [19]
Nu 0 = 5 + 0.025(RePr) 0.8 (9)
для теплообмена в жидких металлах при вынужденном турбулентном течении в трубе с условием на ее границе второго рода: q = const.
-
3. Результаты
-
3.1. Влияние магнитного поля без учета термогравитационной конвекции
Численное моделирование проводилось для числа Рейнольдса Re, равного 10 4 и 1.2 · 10 4 , и вариаций чисел Гартмана Ha до 550 (при этом число Стюарта N ∼ 30) и Ричардсона Ri до 2.4. Во всех рассчитанных вариантах выход на квазистационарные режимы длился не более ∼ 60 безразмерных конвективных единиц (1 к.е. составляет ∆t/(d/U 0 )). За это время флуктуации среднеобъемной кинетической энергии потока становились относительно малыми. Для отыскания результатов после выхода на квазистационарный режим рассчитываемые при решении уравнений (1) – (5) нестационарные поля скорости и температуры усреднялись за период в ∼ 100 к.е., равный удвоенному времени перемещения потока через исследуемую область и поэтому достаточный для получения параметров установившегося потока.
При пренебрежении термогравитацией (Ri = 0) влияние поперечного магнитного поля на вынужденное течение проводящей жидкости в трубе можно разделить на «внешнее» — воздействие на усредненное поле продольной скорости, которое приводит к формированию течения с профилем скорости Гартмана, и так называемое «структурное» — воздействие на флуктуации скорости, которое способствует подавлению турбулентности потока [5] .
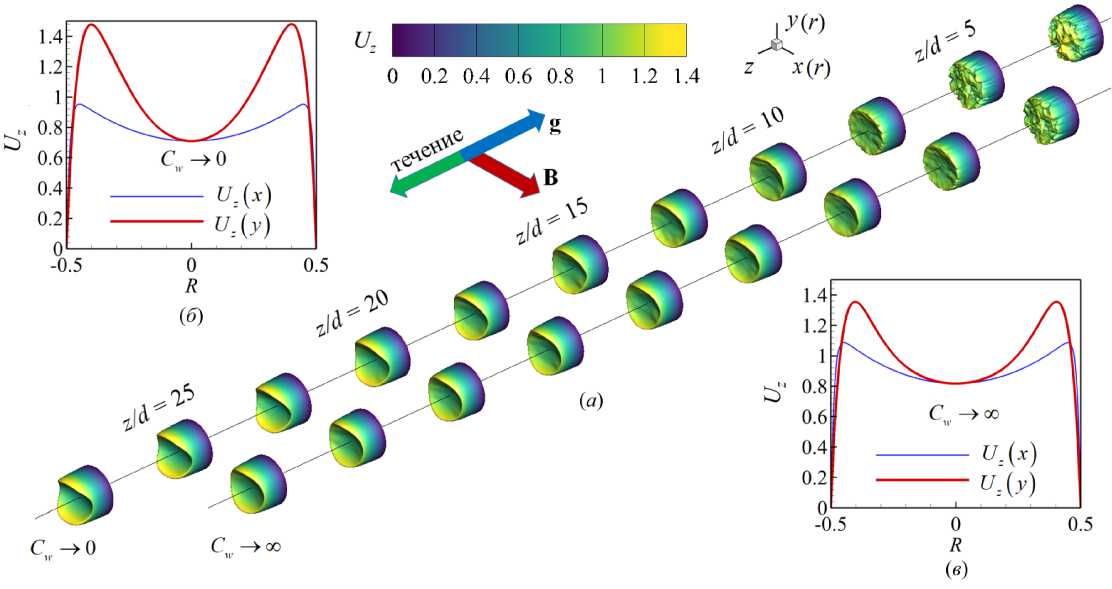
На рисунке 2а представлены картины мгновенных полей продольной компоненты скорости в потоке жидкости по мере продвижения по трубе при разных условиях. Во входной области (z/d = 0) продольная скорость соответствует развитому турбулентному течению. При попадании потока в область магнитного поля (z/d = 5) течение вниз по потоку трансформируется. Видно, что, во-первых, нарушается осевая симметрия поля скорости и, во-вторых, уменьшаются возмущения скорости — мгновенное поле становится более сглаженным.
Представленные на рисунке 2б , в профили усредненной во времени продольной скорости U z вдоль осей координат в поперечном сечении трубы (z/d = 37), находящемся вдали от входной области магнита, в котором течение уже установившееся. В случае изолированных стенок (Рис. 2б ) происходит сильное «уплощение»
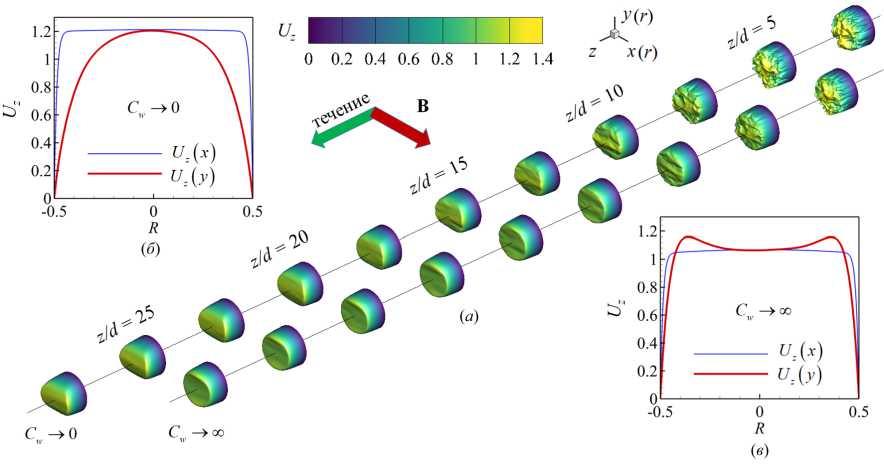
Рис. 2. Вид мгновенного поля продольной компоненты скорости U z ( а ) в разных сечениях входного участка z/d ∈ [0;25] трубы с изолированными ( C w → 0 ) и идеально проводящими ( C w → ∞ ) стенками; профили осредненной скорости вдоль осей x (тонкая линия) и y (толстая линия) в сечении z/d= 37 при изолированных ( б ) и идеально проводящих ( в ) стенках; Re= 10 4 , Ha= 100 , Ri=0
профиля скорости (см. U z в плоскости (x,z) вдоль направления магнитного поля, в то время как в плоскости (y,z) в перпендикулярном магнитному полю направлении имеет место лишь торможение в центральной части потока (см. U z ). При идеально проводящих стенках (Рис. 2в ) уплощение профиля в плоскости (x,z) вдоль магнитного поля сохраняется, но градиент скорости несколько снижается, а скорость потока меньше, чем при изолированных стенках (Рис. 2б ), при этом в плоскости (y,z) перпендикулярно магнитному полю формируется М-образный профиль скорости.
Механизм такой трансформации известен [20] и подтверждается с помощью анализа распределений индуцированных электрических токов в поперечном сечении трубы z/d = 37, которые представлены на рисунке 3. В формирующихся вблизи стенок слоях Гартмана, перпендикулярных полю (x/d = ± 0.5 или ф = { п/2,3п/2 } ), при непроводящих стенках (C w ^ 0, Рис. 3а ) плотность электрического тока выше, чем в случае их идеальной проводимости (C w ч ^ , Рис. 3б ), так как часть тока замыкается на стенку. Эти электрические токи, взаимодействуя с магнитным полем, ускоряют жидкость в «гартмановских» слоях, поэтому скорость и градиент скорости в них при непроводящих стенках несколько выше. При поддерживаемом постоянном расходе через трубу с идеально проводящими стенками скорость жидкости должна вырасти в областях, в которых ортогональная магнитному полю компонента плотности электрического тока минимальна. Эта область поперечного сечения соответствует так называемым слоям Робертса, тоже расположенных вблизи стенок (y/d = ± 0.5 или ф = { 0,п } ), но параллельных магнитному полю. Именно в них образуются максимумы скорости, которые приводят к возникновению М-образных профилей.
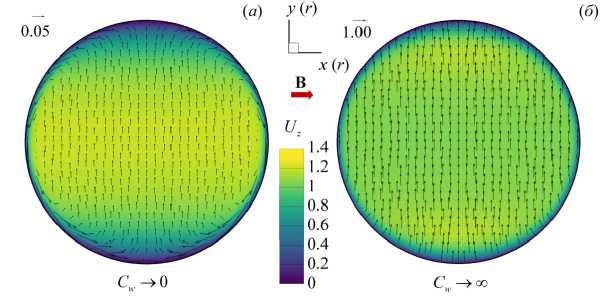
Рис. 3. Усредненное поле продольной скорости U z и векторное поле индуцированного электрического тока J в поперечном сечении z/d = 37 в трубе с изолированными ( а ) и идеально проводящими ( б ) стенками при Re = 10 4 , Ha= 100 , Ri = 0 (числа под стрелкой означают масштабы векторов на соответствующем рисунке)
Подавление турбулентности потока проявляется в уменьшении флуктуаций у компонент вектора скорости. На рисунке 4 показано мгновенное поле продольной компоненты скорости в осевом сечении плоскостью, перпендикулярной направлению магнитного поля. Видно, что масштаб и величина ее флуктуаций после входа меняются вниз по потоку в сторону зоны действия однородного магнитного поля (z/d > 5). При обоих условиях проводимости стенки трубы сначала подавляются мелкомасштабные флуктуации, а затем в направлении от стенки к центру сечения, ослабевают и крупномасштабные, но сохраняют, тем не менее, свое присутствие в центральной части трубы.
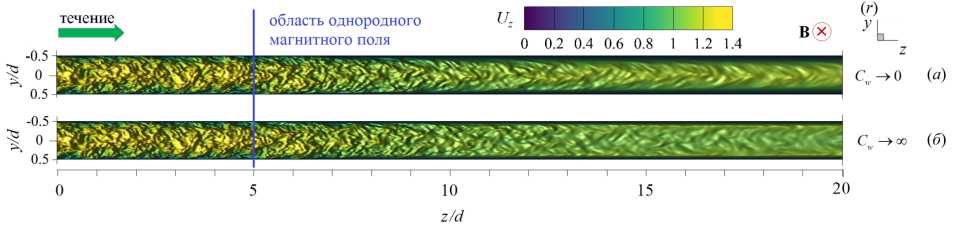
Рис. 4. Мгновенное поле продольной компоненты скорости U z в осевом сечении плоскостью (y,z) (то есть перпендикулярно магнитному полю) в трубе на участке z/d G [0;20] с изолированными ( а ) и идеально проводящими ( б ) стенками при Re = 10 4 , Ha= 100 , Ri = 0 ; поле представлено в виде поверхности f = U z (y,z)
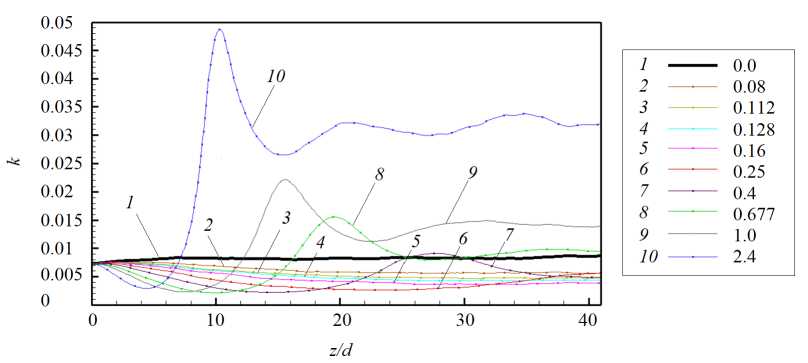
На рисунке 5 представлено изменение по длине трубы средней по сечению кинетической энергии флуктуаций скорости (k = (1/2) / Ui’2). Видно,
что при достижении сечения z/d =20 поток уже можно считать полностью ламинарным при обоих условиях проводимости стенки. При этом уменьшение энергии флуктуаций для идеально проводящей стенки происходит несколько быстрее.
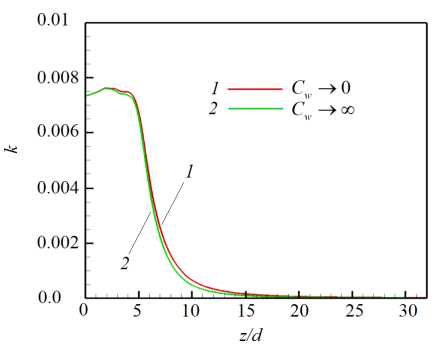
Рис. 5. Распределение средней по сечению трубы кинетической энергии флуктуаций скорости ( k ) по длине канала для двух предельных случаев проводимости при Re= 10 4 , Ha= 100 , Ri=0
-
3.2. Влияние термогравитации в отсутствие магнитного поля
В отсутствие магнитного поля (Ha = 0) влияние силы плавучести при подъемном турбулентном течении в обогреваемой трубе (имеет место устойчивая стратификация плотности g o (dp/dz) > 0) проявляется в виде «внешнего» воздействия на усредненный профиль продольной скорости, который имеет тенденцию трансформации к М-образной, но осесимметричной форме, и «структурного» воздействия на турбулентный перенос [4] . На рисунке 6а представлено развитие мгновенных полей продольной компоненты скорости потока вдоль течения по длине обогреваемой трубы для двух различных значений числа Ричардсона Ri = { 0.16,0.677 } . В обоих случаях поля продольной компоненты скорости претерпевают значительные изменения, но сохраняют осевую симметрию. При меньшем значении (Ri = 0.16, Рис. 6б ) вниз по потоку заметно уменьшение пространственной неоднородности поля скорости, что можно считать «структурным» влиянием плавучести на флуктуации скорости, вместе с тем в центре трубы скорость снижается, усредненный профиль продольной скорости приобретает М-образную форму (Рис. 6б ). При большем значении (Ri = 0.677, Рис. 6в ) «структурное» воздействие остается прежним, а «внешнее» — усиливается, М-образность усредненного профиля продольной скорости становится более выраженной.
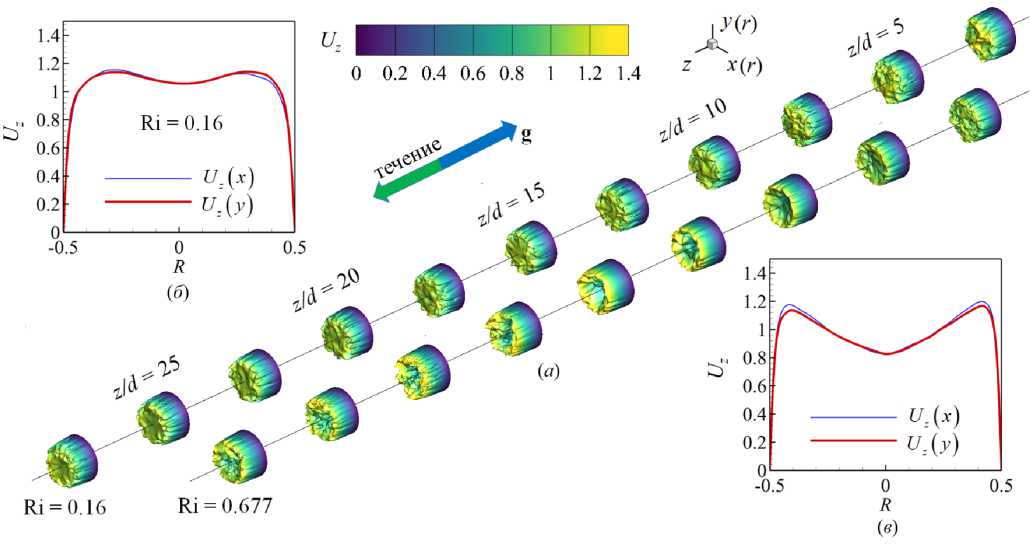
Рис. 6. Мгновенное поле продольной компоненты скорости U z ( а ) в трубе на входном участке z/d ∈ [0;25] и профили осредненной скорости вдоль осей x (тонкая линия) и y (толстая линия) в сечении z/d = 37 при Re = 10 4 , Ha = 0 и разных числах Ri : 0.16 ( б ) и 0.677 ( в )
На рисунке 7 показано мгновенное поле продольной компоненты скорости в осевом сечении плоскостью (y,z) для двух рассматриваемых значений Ri на начальном участке обогрева z/d G [0;20]. Видно, что при малом Ri (Рис. 7а ) преобладает «структурное» влияние с уменьшением флуктуаций скорости, апри большем Ri (Рис. 7б ) явно превалирует «внешнее» воздействие: поле скорости сильно трансформируется по длине обогреваемой области.
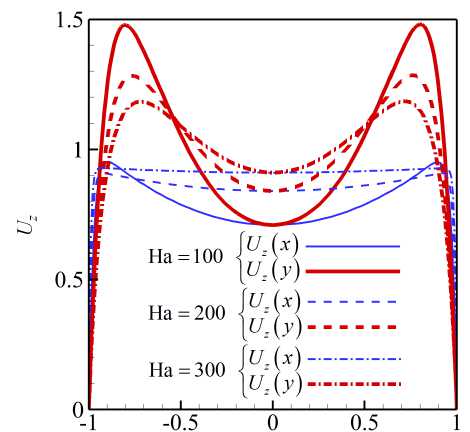
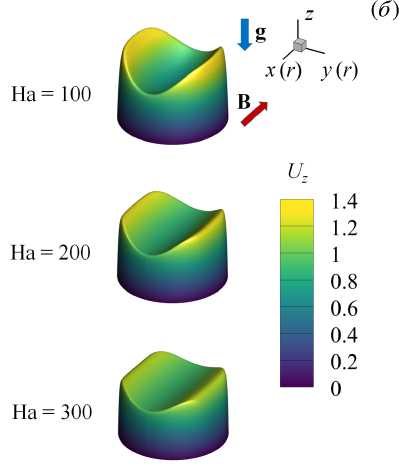
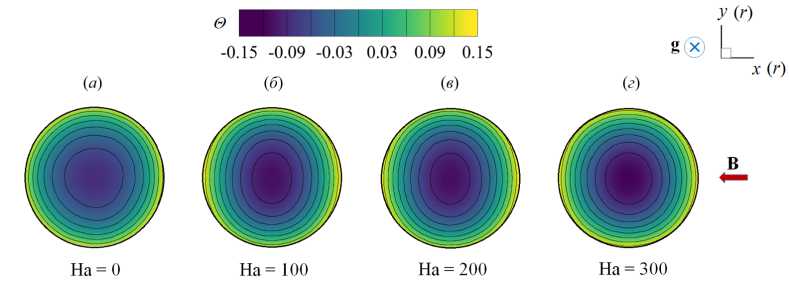
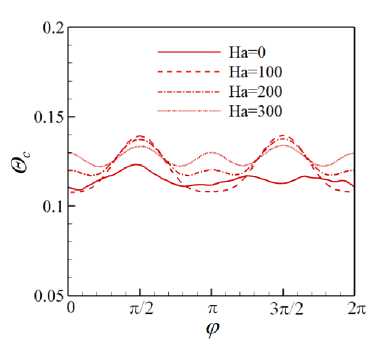
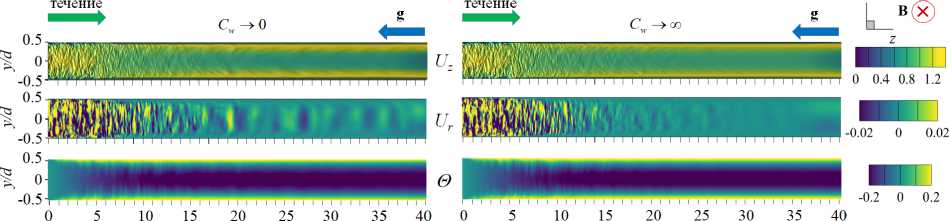
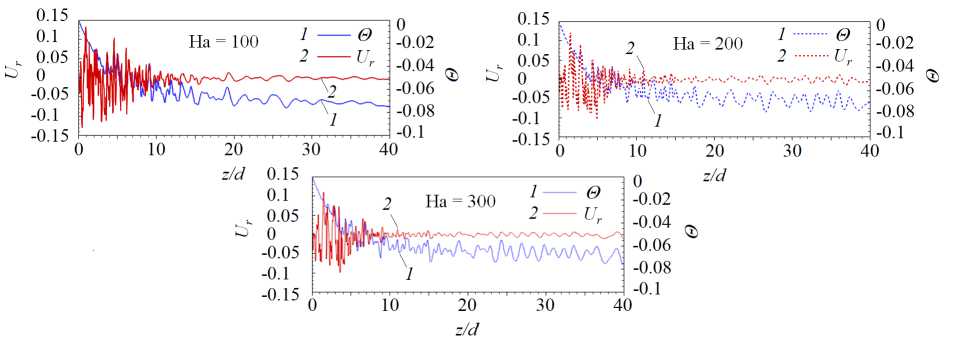
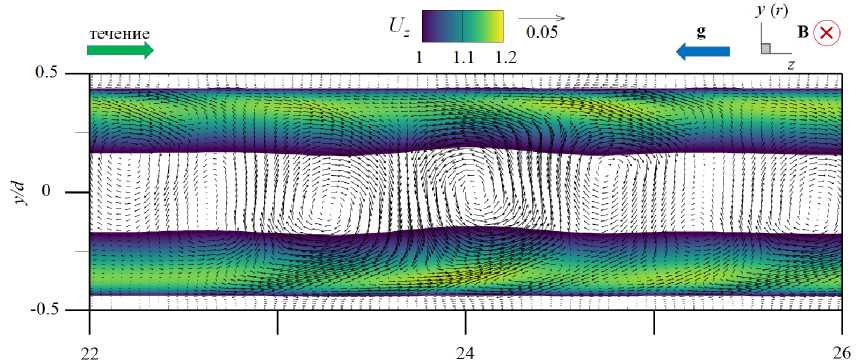
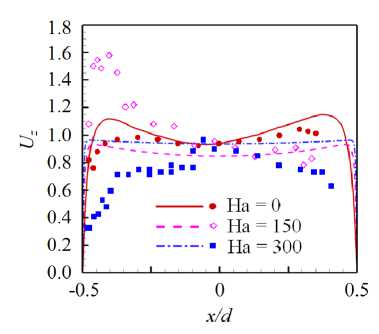
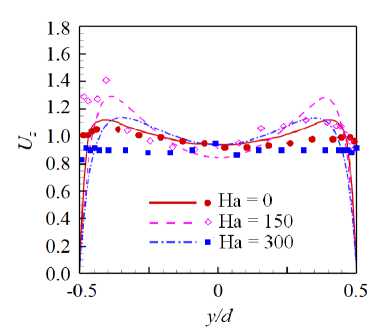
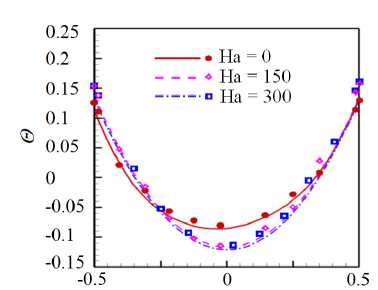
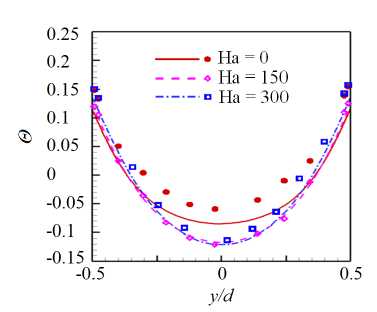
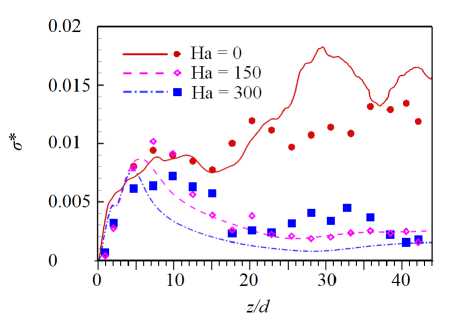
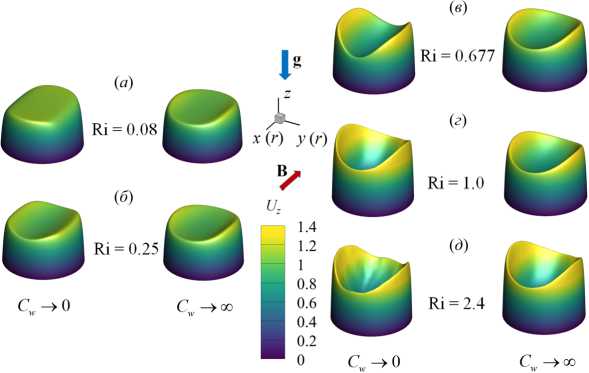
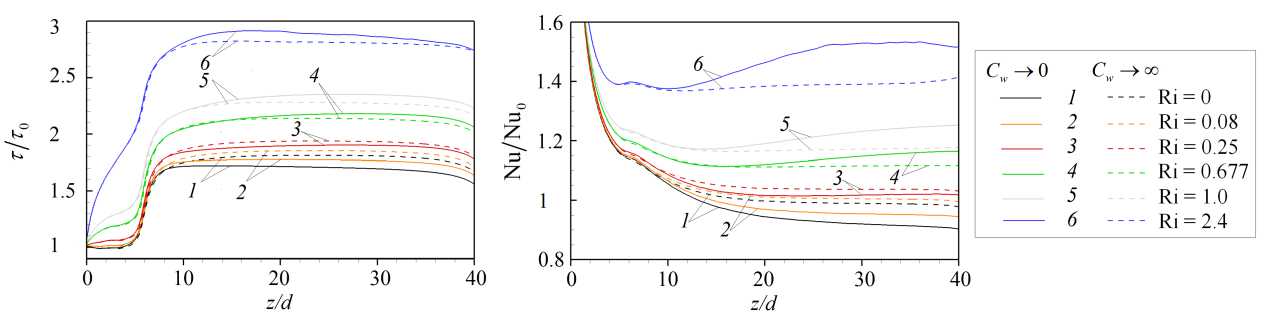
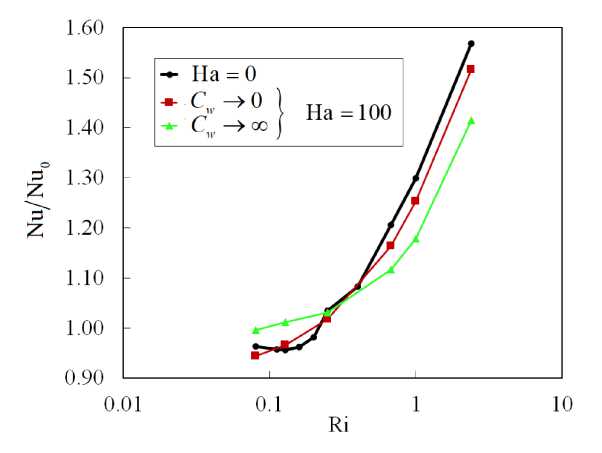
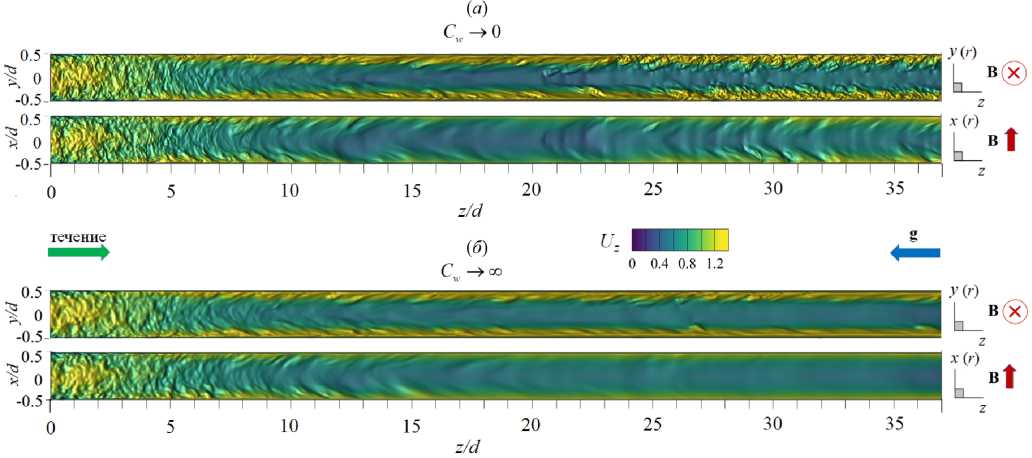
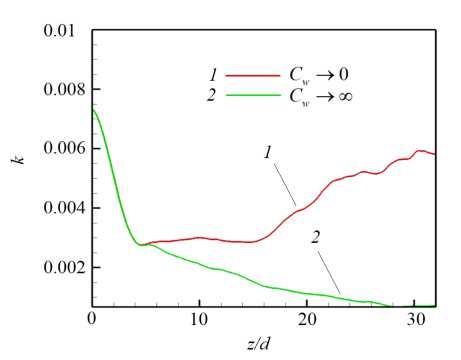
На рисунке 8 представлено распределение по длине обогреваемого участка средней по сечению трубы кинетической энергии флуктуаций скорости для различных Ri в диапазоне от 0 до 2.4. Эти данные свидетельствуют, что при относительно низких значениях (Ri < 0.25) практически во всей исследуемой области происходит снижение энергии флуктуаций по сравнению с вынужденной турбулентной конвекцией (Ri = 0), то есть наблюдается подавление турбулентного переноса. Для Ri > 0.25 на начальном участке (от 0 < z/d < 5 для Ri = 2.4 до 0 z/d Рис. 7. Мгновенное поле продольной компоненты скорости Uz в осевом сечении плоскостью (y,z) в трубе на обогреваемом участке z/d G [0;20] при Re =104, Ha = 0 и разных числах Ri: 0.16 (а) и 0.677 (б); поле представлено в виде поверхности f = Uz (y,z) Рис. 8. Распределение средней по сечению трубы кинетической энергии флуктуаций скорости k по длине канала для разных значений Ri при Re =104, Ha = 0 3.3. Совместное влияние магнитного поля и термогравитационной конвекции Совместное влияние магнитного поля и термогравитационной конвекции проявляется в «конкуренции» двух массовых сил — пондеромоторной силы и силы плавучести, которые определяют «внешнее» воздействие на поле скорости потока. Сила плавучести осесимметрично ускоряет поток вблизи стенки. А пондеромоторная сила активизирует поток около «гартмановских» стенок (x/d = ±0.5 или ф = {п/2, 3п/2}) и замедляет его в центральной части поперечного сечения, при этом в области течения, содержащей слои Робертса вблизи стенок (y/d = ±0.5 или ф = {0, п}), ее роль минимальна; следовательно, от действия пондеромоторной силы поля продольной скорости потока теряют осевую симметрию. Все это видно на рисунке 9а, на котором показано развитие мгновенных полей продольной компоненты скорости потока вдоль течения по длине трубы для двух условий проводимости стенки при фиксированных Ha = 100 и Ri = 0.677. Максимум продольной скорости потока локализуется вблизи образующей трубы, параллельной магнитному полю (ф = {п/2,3п/2}), так как в этих областях индуцируемые в жидкости токи не чувствительны к магнитному полю (см. подраздел 3.2). Влияние проводимости стенки трубы заключается в «перераспределении» потока в поперечном сечении. На рисунке 9б, в приведены профили усредненной продольной скорости вдоль осей координат в поперечном сечении трубы (z/d = 37), соответствующей установившемуся течению вдали от входной области магнита. Видно, что для изолированных стенок (Рис. 9б) неоднородность поля продольной скорости выражена сильнее, чем в случае идеально проводящих стенок (Рис. 9в): в осевой плоскости, перпендикулярной магнитному полю (толстая линия), максимум продольной скорости выше, а минимум заметно ниже. Рис. 9. Мгновенное поле продольной компоненты скорости Uz (а) в трубе на входном участке z/d ∈ [0;25] с изолированными (б) и идеально проводящими (в) стенками и профили осредненной скорости вдоль осей x (тонкая линия) иy (толстая линия) в сечении z/d=37приизолированных (б) и идеально проводящих (в) стенках; Re= 104, Ha=100иRi=0.677 При увеличении числа Ha максимумы усредненной продольной скорости в области установившегося течения (z/d = 37) снижаются как в плоскости вдоль магнитного поля (x,z), так и в плоскости, перпендикулярной ему (y,z), что связано с возрастанием роли пондеромоторной силы (Рис. 10). Форма установившегося профиля продольной скорости потока в плоскости, в которой доминируют «струи» вблизи стенок перпендикулярно магнитному полю (y/d=±0.5 или ф = {0,п}), влияет на поле температуры и приводит к его асимметрии относительно оси (Рис. 11). При Ha = 0 (Рис. 11 а) усредненное поле температуры в потоке в поперечном сечении z/d = 37 практически симметрично, но уже при Ha = 100 (Рис. 11 б) наблюдается асимметрия, при которой изотермы «вытянуты» в поперечном магнитному полю направлении. При дальнейшем увеличении числа Гартмана симметрия полей температуры восстанавливается (Рис. 11в, г), что соответствует изменениям в профиле скорости (Рис. 10б ). Распределение безразмерной температуры стенки по периметру в сечении z/d = 37 для различных значений Ha представлено на рисунке 12. Видно, что при Ha=100 наблюдается максимум температуры стенки в области слоев Гартмана (ф = {п/2,3п/2}), так как продольная скорость потока здесь ниже, чем вблизи стенки в области слоев Робертса (ф = {0,п}) (см. Рис. 10а). С ростом величины числа Гартмана температура стенки выравнивается: при ф = п/2 и ф = 3п/2 температура несколько снижается, а при ф = 0 и ф = п растет, поэтому в среднем по периметру теплоотдача падает. Рис. 10. Профили вдоль осей x (тонкая линия) и y (толстая линия) (а) и поля (б) усредненной продольной компоненты скорости Uz в сечении z/d=37в случае изолированных стенок при Re= 104, Ri = 0.677 и разных значениях числа Гартмана Рис. 11. Поле безразмерной температуры 0 в сечении в сечении z/d = 37 трубы в случае изолированных стенок при Re = 104, Ri = 0.677 и разных значениях числа Гартмана Рис. 12. Распределение усредненной безразмерной температуры стенки Θc по периметру трубы в сечении z/d = 37 в случае изолированных стенок при Re = 104, Ri = 0.677 и разных значениях числа Гартмана Как и в случае без обогрева (см. подраздел 3.1), магнитное поле быстро подавляет турбулентные флуктуации скорости, начиная от входа в магнитное поле z/d = 5, причем в условиях идеально проводящей стенки процесс происходит несколько быстрее. Рисунок 13 содержит мгновенные поля продольной и поперечной компонент скорости потока и безразмерной температуры, отсчитанной от среднемассовой температуры жидкости для Ha= 100. Видно, что при непроводящей стенке (Cw ^ 0, Рис. 13а) крупномасштабные флуктуации продольной скорости Uz и температуры Θ сохраняются по всей длине обогреваемой области. При этом поперечная скорость Ur имеет чередующиеся минимумы и максимумы с амплитудой ∼1–2% от средней расходной скорости в области z/d € [15;30], которые свидетельствуют о наличии движения жидкости поперек основного течения. Для идеально проводящей стенки (Cw → ∞, Рис. 13б) флуктуации скорости и температуры практически исчезают при z/d> 15, а поле поперечной компоненты скорости Urк концу зоны обогрева выравнивается до нуля. (а) (б) У (О z/d z/d Рис. 13. Мгновенное поле продольной (Uz) и поперечной (Ur) компонент скорости, а также безразмерной температуры 0, в осевом сечении плоскостью (y, z) в трубе на участке z/d 6 [0;40] с изолированными (а) и идеально проводящими (б) стенками при Re = 104, Ha= 100 и Ri = 0.677; поле Uz представлено в виде поверхности f = Uz (y,z) (в продольном направлении масштаб уменьшен в 4 раза) При изменении числа Ha в условиях непроводящих стенок (Cw ^ 0) флуктуации скорости и температуры в потоке не затухают, что видно на рисунке 14, где по длине обогреваемого участка трубы показаны изменения величин мгновенной поперечной скорости Ur и температуры 3 в точке с координатой R = r/d = 0.25 и ф = 0, которая расположена в плоскости (y,z), перпендикулярной магнитному полю. На входном участке z/d € [0;5] наблюдаются турбулентные флуктуации скорости и температуры, затем на участке z/d € [5;15] они снижаются, происходит подавление турбулентности. Тем не менее флуктуации не затухают полностью, даже при увеличении числа Ha, и до конца зоны обогрева остаются и совершаются c амплитудой на уровне ^1-2% от средней скорости и ∼5–10% (в данном случае 0.1–0.2 ºC) от температурного перепада «жидкость–стенка». Флуктуации скорости, по-видимому, связаны с потерей устойчивости струями, которые формируются в области Рис. 14. Изменение по длине обогреваемой области мгновенных значений поперечной компоненты скорости Ur и безразмерной температуры О в точке R = r/d = 0.25 осевого сечения плоскостью (y,z) (ф = 0)в трубе с изолированными стенками при Re = 104, Ri = 0.677 и разных значениях числа Гартмана слоев Робертса (ф = {0,п}) (см. Рис. 10). На рисунке 15 изображено мгновенное поле продольной компоненты скорости и векторное поле флуктуаций скорости Ur′,Uz′в осевом сечении плоскостью (y,z) на участке обогреваемой области z/d G [22;26] при Ha = 300. Вблизи обогреваемой стенки струи развиваются и время от времени обрываются по длине. Вследствие этого образуется вихревое движение, причем оси вихрей располагаются вдоль магнитного поля, поэтому не подавляются им. Поскольку жидкость периодически перемещается из более нагретой области возле стенки в менее нагретую центральную часть поперечного сечения, возникают флуктуации температуры (см. Рис. 14). Рис. 15. Мгновенное поле продольной компоненты скорости Uz и векторное поле флуктуаций скорости Ur,Uzв осевом сечении плоскостью (y,z) в трубе с изолированными стенками на участке z/d € [22;26] при Re= 104, Ha = 300 и Ri = 0.677 3.4. Сравнение с экспериментом В данном разделе проводится сравнение результатов авторских расчетов с экспериментом из [11] для течения в режиме с Re = 1.2 • 104 при Ha = {0,150,300} и Ri = 0.47 (соответствует тепловому потоку q = 30 кВт/м2в эксперименте) при изолированной стенке (Cw ^ 0). Такой предельный случай проводимости стенки находится ближе к условиям эксперимента, в котором точное значение установить невозможно, а в своих работах величина проводимости стенки авторами оценивается как Cw ~ 0.01. На рисунке 16 показаны усредненные профили продольной скорости в сечении z/d = 37 и экспериментальные данные для сравнения. Качественное соответствие результатов наблюдается лишь дляHa=0. Возможная причина заключается в том, что в эксперименте для измерения продольной скорости используется корреляционная методика, применение которой затруднено в условиях подавления флуктуаций магнитным полем при Ha= {150,300} [21]. Рисунок 17 содержит усредненные профили безразмерной температуры, отсчитанные от ее среднемассовой (a) Рис. 16. Профили усредненной продольной компоненты скорости Uz вдоль осей x (а) и y (б) в сечении z/d= 37в случае изолированных стенок при Re = 1.2· 104, Ri = 0.47 и разных значениях числа Гартмана; точки – экспериментальные данные из работы [11] (a) Рис. 17. Профили усредненной безразмерной температуры Θ вдоль осей x (а) и y (б) в сечении z/d = 37 в случае изолированных стенок при Re = 1.2· 104, Ri = 0.47 и разных значениях числа Гартмана; точки – экспериментальные данные из работы [11] величины в сечении z/d = 37 и, для сравнения, экспериментальные данные. Наблюдается неплохое качественное и количественное соответствие результатов. Неоднородность температуры в магнитном поле выражена сильнее, при этом за счет ухудшения теплоотдачи температура на стенке выше, чем при Ha = 0. Кроме того, в магнитном поле температура стенки на образующей трубы, перпендикулярной магнитному полю 0 (x/d = ±0.5) (Рис. 17а), несколько выше, чем температура стенки на образующей трубы, параллельной полю 0 (y/d = ±0.5) (Рис. 17б), что объясняется более высокими значениями скорости вблизи стенки в области y/d = ±0.5 (см. Рис. 16). Распределение по длине трубыбезразмерной интенсивности флуктуаций температуры (ст* = a/(qd/X) = V 0 ‘2) вблизи обогреваемой стенки R = r/d = 0.4 и ф = 0 показано на рисунке 18. В отсутствие магнитного поля (Ha = 0) изменение интенсивности флуктуаций отражает структурные изменения потока по длине обогреваемого участка Рис. 18. Изменение безразмерной интенсивности температурных пульсаций σ∗= σ/(qd/λ) вблизи обогреваемой стенки в точке R= r/d= 0.4 (в плоскости поперечной магнитному полю φ = 0) по длине обогреваемого участка в случае изолированных стенок при Re= 1.2· 104, Ri = 0.47 и различных значениях числа Гартмана; точки – экспериментальные данные из работы [11] трубы. От начала обогрева до z/d= 10 возмущения нарастают, что связано с нагревом турбулентного потока. Затем в диапазоне z/d∈[10;15] интенсивность снижается из-за ламинаризации потока (структурный эффект силы плавучести, см. п. 3.2). Последующий рост в диапазоне z/d∈[15;20] отражает внешнее воздействие, а именно перестройку профиля скорости. Далее интенсивность флуктуаций температуры выходит на стабилизированный уровень, соответствующий развитой турбулентной конвекции. Интенсивность флуктуаций температуры составляет в этом случае порядка 1 ºC. Видно, что в магнитном поле с ростом числа Ha интенсивность флуктуаций падает примерно на порядок и достигает максимального значения 0.2 ºC. Наблюдается неплохое качественное совпадение результатов расчета с данными эксперимента из [11]. Однако есть количественные различия, особенно для Ha= 0 и Ha = 300 в области z/d ∈[25;35], что вызвано в расчете, возможно, недостаточным, по сравнению с экспериментом, временем осреднения. 3.5. Параметрический анализ Авторами выполнен параметрический анализ течения при фиксированных числах Re = 104и Ha = 100 для двух предельных значений проводимости стенки (Cw →0 и Cw → ∞) и при вариации Ri от 0 до 2.4. На рисунке 19 для разных значений числа Ri представлены усредненные поля продольной скорости в поперечном сечении трубы z/d= 37 от начала обогрева. Анализ показывает, что для обоих условий проводимости стенок при увеличении Ri под действием силы плавучести в областях, вблизи слоев Робертса (y/d = ±0.5), ощутимо возрастает продольная скорость. Это объясняется тем, что здесь сопротивление, вызванное действием пондеромоторной силы, меньше. В то же время в областях вблизи «гартмановских» стенок (x/d = ±0.5) продольная скорость возрастает не так ощутимо в виду тормозящего действия пондеромоторной силы. Рис. 19. Поля усредненной продольной компоненты скорости Uz в сечении z/d = 37 от начала обогрева при изолированных ((а)–(д) слева) и идеально проводящих ((а)–(д) справа) стенок при Re = 104, Ha = 100 и разных значениях числах Ричардсона Ri: 0.08 (а); 0.25 (б); 0.677 (в); 1.0 (г); 2.4 (д); поле представлено в виде поверхности f = Uz (x,y) Следует отметить, что для небольших значений числа Ричардсона Ri (до 0.25, Рис. 19а, б) продольная скорость вблизи слоев Робертса (стенка y/d= ±0.5 и φ= {0,π}) при идеально проводящих стенках (Cw → ∞) выше, чем при изолированных (Cw → 0). Для больших значений (Ri > 0.25, Рис. 19в–д), напротив, в случае изолированных стенок (Cw → 0) максимумы продольной скорости вблизи стенки в областях y/d= ±0.5 ощутимо выше, чем при идеально проводящих стенках (Cw → ∞). Таким образом, можно предположить, что для фиксированного значения Ha существует определенная граница по значению Ri, при достижении которой «внешнее» воздействие силы плавучести на течение начинает преобладать над «внешним» воздействием пондеромоторной силы. Это обстоятельство определяет характер зависимостей сопротивления и теплоотдачи. На рисунке 20 приведены графики зависимостей среднего по периметру трубы касательного напряжения на стенке (Рис. 20а) и среднего числа Nu (Рис. 20б), отнесенных к соответствующим величинам для турбулентного течения в трубе при заданном числе Re в отсутствие магнитного поля и влияния силы плавучести (то есть к τ0 = 0.0038, см. формулу (6), и к Nu0 = 7.22, см. формулу (9)), по длине обогреваемой части трубы для различных значений числа Ri. Для всех кривых на рисунках 20а, б характерен начальный участок z/d∈[0;15], на котором формируются поля скорости и температуры, поэтому именно здесь касательные напряжения и теплоотдача существенно изменяются. Затем, начиная с z/d= 20, значения сопротивления и теплоотдачи стабилизируются, что свидетельствует об установившемся течении. Рост поперечных градиентов скорости под действием массовых сил приводит к увеличению стабилизированных значений касательных напряжений по сравнению с аналогичными значениями вынужденного турбулентного течения. Видно, что вплоть до Ri = 0.25 значения касательных (а) (б) Рис. 20. Средние по периметру относительные величины касательных напряжений на стенке (а) и чисел Нуссельта (б): изменение по длине обогреваемого участка в случае изолированных (сплошные линии) и идеально проводящих (пунктирные линии) стенок при Re= 104, Ha= 100 и значениях Ri от 0 до 2.4 напряжений и число Nu при изолированных стенках (Cw→ 0) ниже, чем при идеально проводящих (Cw→ ∞). При дальнейшем увеличении числа Ричардсона (Ri=0.677ивыше) продольная скорость в области слоев Робертса (стенка y/d=±0.5 и φ= {0,π}) при условии Cw →0 растет интенсивнее, поэтому напряжения и теплоотдача в этом случае выше, чем для идеально проводящих стенок (Cw→ ∞) (см. Рис. 19в–д). Рис. 21. Зависимости среднего числа Нуссельта в сечении z/d = 37 в случае изолированных (сплошные линии) и идеально проводящих (пунктирные линии) стенок от числа Ричардсона при Re= 104и Ha= 100; для сравнения приведена зависимость для Ha=0 Средние значения коэффициентов теплоотдачи в области установившегося течения в сечении z/d = 37 от начала обогрева, отнесенные к значению коэффициента теплоотдачи вынужденного турбулентного течения, рассчитанного по формуле (9) для жидких металлов (Nu0) в зависимости от Ri для разных условий проводимости стенки в магнитном поле с Ha= 100, представлены на рисунке 21. Здесь же, для сравнения, приведены результаты для течения без воздействия магнитного поля (Ha = 0). В отсутствие магнитного поля коэффициент теплоотдачи растет при увеличении Ri, за исключением узкой области 0.1 < Ri < 0.2, где наблюдается его незначительное снижение, связанное с подавлением турбулентного переноса (из-за «структурного» эффекта, обсуждаемого в подразделе 3.2). В магнитном поле, в случае изолированных стенок теплоотдача ухудшается по причине подавления турбулентности магнитным полем. В то же время, несмотря на подавление турбулентности при низких Ri (то есть Ri < 0.25), коэффициент теплоотдачи при идеально проводящих стенках даже выше, чем в отсутствие магнитного поля, что можно объяснить формированием в потоке М-образного профиля скорости в плоскости перпендикулярно магнитному полю. При увеличении Ri ситуация меняется: М-образность выражается сильнее при изолированных стенках, поэтому коэффициент теплоотдачи в этих условиях на 5–7% выше, чем для идеально проводящих стенок, но, тем не менее, он всегда остается ниже, чем при отсутствии магнитного поля (Ha = 0). С ростом Ri снижается влияние магнитного поля не только на усредненные профили продольной скорости (см. Рис. 19д), но и на структуру течения. При больших значениях Ri «структурный» эффект плавучести приводит к дополнительной турбулизации потока (см. подраздел 3.2), а при наличии магнитного поля — к появлению неустойчивости струй вблизи стенок в плоскости перпендикулярно магнитному полю (см. подраздел 3.3), там, где величина продольной скорости максимальна. Два этих фактора при Ri = 2.4 способствуют развитию течения, при котором в области вблизи слоев Робертса (φ= {0,π}) оно становится турбулентным, ав остальной части потока ламинаризуется. На рисунке 22 показаны мгновенные поля продольной скорости потока для Ha = 100 и Ri = 2.4 в осевых плоскостях (y,z) и (x,z) на участке обогреваемой области z/d∈[0;37] для двух вариантов проводимости стенки. После входа в обогреваемый участок поля продольной скорости течения в зоне z/d ∈[0;10] принимают М-образную форму, качественно соответствующие рисунку 19д. Затем в зоне z/d∈[10;20] происходит ламинаризация потока во всей области. Видно, что в плоскости (x,z) в направлении поля возмущения подавляются быстрее, чем в плоскости (y,z), так как электрические токи, протекающие вблизи «гартмановских» стенок (x/d = ±0.5) (см. Рис. 3) определяют область джоулевой диссипации энергии. На рисунке 22 также видно, что при идеально проводящей стенке (Cw → ∞, Рис. 22б) уровень ламинаризации потока гораздо выше, чем в условиях изолированной стенки (Cw→ 0, Рис. 22а). Несмотря на то, что течение становится безвихревым, вблизи обогреваемой стенки для Рис. 22. Вид мгновенного поля продольной (Uz) компоненты скорости в осевом сечении плоскостями (y,z) ((а) и (б), сверху) и (x,z) ((а) и (б), снизу) в трубе на участке z/d G [0;37] с изолированными (а) и идеально проводящими (б) стенками при Re = 104, Ha = 100, Ri = 2.4; поле Uz представлено в виде поверхности f = Uz (y,z) (масштаб в продольном направлении уменьшен в 2 раза) обоих обсуждаемых условий ее проводимости остается область течения с возмущениями скорости, которые носят периодический характер. Возмущения нарастают критически в зоне z/d ~ 20 для изолированной стенки (Cw ^ 0, Рис. 22а). Видно, что вблизи стенки (y/d = ±0.5 в плоскости (y,z)) возникают пространственные структуры с неоднородной скоростью, качественно похожие на вихревые структуры с осями, ориентированными вдоль направления магнитного поля, и распространяющиеся в потоке на протяжении всей зоны обогрева. Их кинетическая энергия растет, начиная от z/d ~ 20 и до конца зоны обогрева (Рис. 23). Напротив, для идеально проводящей стенки (Cw ^ то, Рис. 22б) подобные структуры не развиваются, флуктуации скорости заметно ниже по всей длине рассматриваемой области потока, а их энергия постепенно убывает по длине обогреваемой области (Рис. 23). Рис. 23. Распределение средней по сечению трубы кинетической энергии флуктуаций скорости k по длине обогреваемой области для двух предельных случаев проводимости и Re= 104, Ri = 2.4, Ha= 100 4. Выводы С помощью прямого численного моделирования исследовалась смешанная конвекция при подъемном течении проводящей жидкости (Pr = 0.025) в круглой обогреваемой трубе в поперечном магнитном поле при Re = 104, 0 < Ri < 2.4 и Ha < 550. Отдельно, для сопоставления с результатами экспериментальной работы на ртути [11], проведены расчеты при Re = 1.2 • 104, Ha = {0,150,300} и Ri = 0.47, которые показали неплохое качественное согласование. При незначительном влиянии термогравитации (Ri < 0.5) магнитное поле подавляет турбулентный перенос, течение ламинаризуется по всей длине рассматриваемой обогреваемой области, флуктуации скорости и температуры в потоке не наблюдаются. Коэффициенты теплоотдачи в этом случае ниже, чем при вынужденном турбулентном течении, а сопротивление трения гораздо выше вследствие формирования течения с «гартмановским» профилем скорости. Наличие проводящей стенки трубы увеличивает сопротивление и теплоотдачу из-за формирования М-образных профилей продольной скорости в сечении плоскостью, перпендикулярной магнитному полю. Значительное влияние термогравитации (Ri > 0.5) является дополнительным фактором, способствующим увеличению продольной компоненты скорости потока вблизи обогреваемой стенки, что приводит к росту сопротивления и теплоотдачи. Фактически течение вблизи стенки носит струйный характер с высокими градиентами скорости в поперечном направлении. Для изолированной стенки трубы этот эффект проявляется сильнее, чем для идеально проводящей стенки, поэтому сопротивление и теплоотдача несколько выше. Струи, формирующиеся вблизи стенок в области слоев Робертса (в плоскости перпендикулярно магнитному полю) имеют тенденцию к потере устойчивости: их периодическое развитие и обрыв являются причиной образования вихревых структур, устойчивых в магнитном поле и вызывающих флуктуации компонент скорости и температуры в потоке. Масштаб флуктуаций температуры относительно невелик и составляет порядка 5–10% от температурного напора «жидкость–стенка», что в пересчете на параметры эксперимента на ртути в работе [11] дает 0.1–0.2 градуса, но в условиях тепловых нагрузок бланкета термоядерного реактора ITER, защищающего внешнюю среду от излучения плазмы, эта оценка может возрасти на порядки, что имеет большую практическую значимость с точки зрения оценки возможности появления термоциклической усталости. Важно отметить, что при увеличении числа Ha, в условиях изолированной стенки флуктуации сохраняются в потоке даже несмотря на снижение значения максимума скорости. Можно предположить, что для каждого числа Ha есть определенный диапазон чисел Ri, при котором возможны такие флуктуации. Авторы убедились в этом при экстремальном увеличении числа Ri до 2.4, при котором в областях с высоким градиентом скорости вблизи стенки фактически развивается квазидвумерные возмущения (Q2D турбулентность). Рассмотренный механизм может быть той самой причиной формирования температурных флуктуаций аномально высокой амплитуды, которые наблюдались в эксперименте [11] при больших числах Рейнольдса (Re ⩾ 20000) и Гартмана (Ha ⩾ 550). Эта гипотеза требует дальнейшей проверки с помощью численного анализа, в котором использование прямого численного моделирования (DNS) осложняется необходимостью применять чрезвычайно подробные сетки для разрешения потоков при столь высоких числах Re. Работа выполнена при поддержке гранта Министерства науки и высшего образования Российской Федерации в рамках Государственного задания № FSWF-2023-0017 (Соглашение № 075-03-2023-383 от 18 января 2023 г.) в сфере научной деятельности на 2023-2025 гг. Численные рассчеты осуществлялись с помощью вычислительного кластера «Фишер» в ОИВТ РАН (Москва).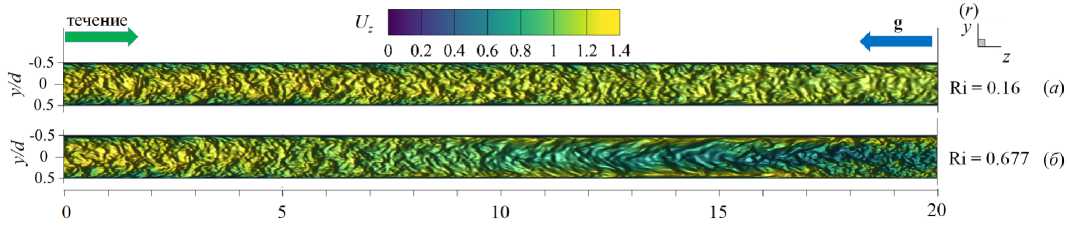
Список литературы Численное моделирование смешанной конвекции в жидком металле при подъемном течении по круглой обогреваемой трубе в условиях поперечного магнитного поля
- Abdou M., Morley N.B., Smolentsev S., Ying A., Malang S., Rowcliffe A., Ulrickson M. Blanket/first wall challenges and required R&D on the pathway to DEMO // Fusion Engineering and Design. 2015a. Vol. 100. P. 2–43. DOI: 10.1016/j.fusengdes.2015.07.021
- Петухов Б.С., Стригин Б.К. Экспериментальное исследование теплообмена при вязкостно-инерционно-гравитационном течении жидкости в вертикальных трубах // Теплофизика высоких температур. 1968. Т. 6, № 5. C. 933–937.
- Jackson J.D., Cotton M.A., Axcell B.P. Studies of mixed convection in vertical tubes // International Journal of Heat and Fluid Flow. 1989a. Vol. 10. P. 2–15. DOI: 10.1016/0142-727x(89)90049-0
- Петухов Б.С., Поляков А.Ф. Теплообмен при смешанной турбулентной конвекции. М.: Наука, 1986. 191 с.
- Jaeger W., Hering W. Mixed Convection with Liquid Metals: Review of Experiments and Model Development // Proc. of the Advances in Thermal Hydraulics. ATH 2018. Orlando, FL, 2018a. P. 846–859.
- Jackson J.D., Axcell B.P., Walton A. Mixed-convection heat transfer to sodium in a vertical pipe // Experimental Heat Transfer. 1994a. Vol. 7, no. 1. P. 71–90. DOI: 10.1080/08916159408946473
- Zikanov O., Belyaev I., Listratov Y., Frick P., Razuvanov N., Sviridov V. Mixed Convection in Pipe and Duct Flows With Strong Magnetic Fields // Applied Mechanics Reviews. 2021a. Vol. 73. 010801. DOI: 10.1115/1.4049833
- Rhodes T.J., Pulugundla G., Smolentsev S., Abdou M. 3D modelling of MHD mixed convection flow in a vertical duct with transverse magnetic field and volumetric or surface heating // Fusion Engineering and Design. 2020a. Vol. 160. 111834. DOI: 10.1016/j.fusengdes.2020.111834
- Vantieghem S., Albets-Chico X., Knaepen B. The velocity profile of laminar MHD flows in circular conducting pipes // Theoretical and Computational Fluid Dynamics. 2009a. Vol. 23. P. 525–533. DOI: 10.1007/s00162-009-0163-0
- Artemov V.I., Makarov M.V., Yankov G.G., Minko K.B. Numerical Investigation of the Effect of the Wall Properties on Downward Mercury Flow and Temperature Fluctuations in a Vertical Heated Pipe under a Transverse Magnetic Field // International Journal of Heat and Mass Transfer. 2024a. Vol. 218. 124746. DOI: 10.1016/j.ijheatmasstransfer.2023.124746
- Лучинкин Н.А., Разуванов Н.Г., Полянская О.Н., Соколов М.А., Бурдюкова Е.А. Исследование теплообмена при подъемном течении жидкого металла в трубе при смешанной турбулентной конвекции, осложненной влиянием магнитного поля // Инженерно-физический журнал. 2022. Т. 95, № 6. C. 1577–1588.
- Votyakov E.V., Kassinos S.C., Albets-Chico X. Analytic models of heterogenous magnetic fields for liquid metal flow simulations // Theoretical and Computational Fluid Dynamics. 2009a. Vol. 23, no. 6. P. 571–578. DOI: 10.1007/s00162-009-0114-9
- Варгафтик Н.Б. Справочник по теплофизическим свойствам газов и жидкостей. М.: Наука, 1972. 721 с.
- Davidson P.A. Introduction to Magnetohydrodynamics. Cambridge, United Kingdom: Cambridge University Press, 2016a. 555 p. . DOI: 10.1017/9781316672853
- Graham R.L., Lubachevsky B.D., Nurmela K.J., Östergård P.R. Dense packings of congruent circles in a circle // Discrete Mathematics. 1998a. Vol. 181, no. 1–3. P. 139–154. DOI: 10.1016/S0012-365X(97)00050-2
- Morinishi Y., Lund T.S., Vasilyev O.V., Moin P. Fully Conservative Higher Order Finite Difference Schemes for Incompressible Flow // Journal of Computational Physics. 1998a. Vol. 143. P. 90–124. DOI: 10.1006/jcph.1998.5962
- Krasnov D., Zikanov O., Boeck T. Comparative study of finite difference approaches in simulation of magnetohydrodynamic turbulence at low magnetic Reynolds number // Computers & Fluids. 2011a. Vol. 50, no. 1. P. 46–59. DOI: 10.1016/j.compfluid.2011.06.015
- Zikanov O., Listratov Y.I., Sviridov V.G. Natural convection in horizontal pipe flow with a strong transverse magnetic field // Journal of Fluid Mechanics. 2013a. Vol. 720. P. 486–516. DOI: 10.1017/jfm.2013.45
- Генин Л.Г., Свиридов В.Г. Гидродинамика и теплообмен МГД-течений в каналах. М.: МЭИ, 2021. 196 с.
- Shercliff J.A. Magnetohydrodynamic pipe flow Part2. High Hartmann number // Journal of Fluid Mechanics. 1962a. Vol. 13. P. 513–518. DOI: 10.1017/S0022112062000890
- Belyaev I.A., Razuvanov N.G., Sviridov V.G., Zagorsky V.S. Temperature correlation velocimetry technique in liquid metals // Flow Measurement and Instrumentation. 2017a. Vol. 55. P. 37–43. DOI: 10.1016/j.flowmeasinst.2017.05.004


