Численное моделирование собственных колебаний частично заполненной жидкостью усечённой конической оболочки в поле силы тяжести
Автор: Бочкарёв С.А., Сенин А.Н.
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 3 т.18, 2025 года.
Бесплатный доступ
Представлены результаты исследований круговых усечённых конических оболочек, частично заполненных идеальной жидкостью, на свободной поверхности которой принимаются во внимание гравитационные эффекты. Математическая постановка задачи динамики упругого тела выполнена на основе вариационного принципа возможных перемещений и соотношений классической теории оболочек, основанной на гипотезах Кирхгофа-Лява. Поведение сжимаемой жидкости описывается уравнениями потенциальной теории, которые вместе с граничными условиями преобразуются к слабой форме с помощью метода Бубнова-Галёркина. Гидродинамическое давление, действующее со стороны жидкости на внутреннюю поверхность оболочки, вычисляется по линеаризованному уравнению Бернулли. Решение задачи осуществляется в осесимметричной постановке с использованием полуаналитического варианта метода конечных элементов. Для вычисления собственных частот применяется метод QR-преобразования. Идентификация связанных мод колебаний в полном частотном спектре реализуется посредством процедуры итерационной динамической конденсации, основанной на методе Мюллера. Достоверность результатов, получаемых в рамках разработанной численной модели, подтверждена путём сравнения с известными данными на примерах упругой и жёсткой оболочек. Проанализировано влияние угла конусности на низшие частоты плескательных и связанных мод колебаний для оболочек с различными граничными условиями (жёсткой заделкой и свободным опиранием на обоих концах, консольным закреплением), разными линейными размерами и уровнем заполнения жидкостью. Продемонстрировано, что характер изменения низших частот колебаний обуславливается величиной угла при вершине и определяется его геометрическими параметрами для связанных мод и не зависит от них в случае плескательных мод.
Усечённая коническая оболочка, классическая теория оболочек, идеальная сжимаемая жидкость, МКЭ, свободная поверхность, плескание, собственные колебания, динамическая конденсация
Короткий адрес: https://sciup.org/143185186
IDR: 143185186 | УДК: 539.3 | DOI: 10.7242/1999-6691/2025.18.3.26
Текст научной статьи Численное моделирование собственных колебаний частично заполненной жидкостью усечённой конической оболочки в поле силы тяжести
При частичном заполнении резервуаров жидкостью её свободная поверхность совершает движение. Это явление, обусловленное воздействием гравитационного поля, известно как плескание [1] . В результате внешних возмущений (сейсмических, вибрационных, возникающих в процессе движения или полёта) колебания свободной поверхности приводят к росту гидродинамической нагрузки, которая может деформировать стенки резервуаров вплоть до потери ими устойчивости или разрушения. Во избежание катастрофических последствий частоты колебаний упругой конструкции и плескания жидкости должны быть достаточно далеки друг от друга в частотном спектре. Чтобы ответить на вопрос, как соблюсти это условие, требуется глубокое изучение процесса колебаний системы «оболочка–жидкость».
Теоретические и экспериментальные исследования тонкостенных тел вращения, частично заполненных жидкостью, как наиболее интенсивно используемых в различных областях техники (в качестве топливных баков ракет-носителей, элементов водопроводных башен, резервуаров для хранения жидкостей различного назначения) имеют длительную историю [2 –4] . В большей степени изучены вертикально и реже горизонтально ориентированные цилиндрические оболочки [5 –40] . В этих работах разными методами в линейной постановке анализируются, как правило, связанные собственные и вынужденные колебания оболочек, в том числе подкреплённых и изготовленных из различных материалов. Объединяет публикации наличие гравитационного граничного условия на свободной поверхности жидкости, описываемой уравнениями потенциальной теории или линеаризованными уравнениями Эйлера. Только в некоторых из работ уделяется внимание плескательным частотам и отвечающим им формам колебаний, но в основном, это касается консольно закреплённых конструкций. В частности, в работе [8] показано, что частота плескания значительно увеличивается только до определённого значения отношения высоты жидкости к радиусу оболочки. В статье [10] представлены зависимости, из которых следует, что частоты плескания возрастают с повышением окружной гармоники. В публикации [12] продемонстрировано, что уровень заполнения оболочки жидкостью оказывает незначительное влияние на частоты плескания. В [20] выявлено, что для фиксированной окружной гармоники имеет место значительное взаимодействие между низшими плескательными и связанными модами, когда частоты колебаний сближаются. Авторы работы [21] показывают, что плескательные колебания жидкости в контейнере могут быть снижены посредством размещения в нём жёстких или упругих перегородок. В статье [22] установлено, что плескательные частоты являются похожими для оболочек с различными комбинациями граничных условий и уровнем подкрепления, если они имеют одинаковые геометрические размеры. Значительное влияние угла армирования на высоту всплеска жидкости в композитной оболочке в случае гармонического и сейсмического воздействий обнаружено в [34] . Двумерные или трёхмерные формы колебаний свободной поверхности получены в работах [7, 11, 16, 20, 25, 35, 38] .
В значительно меньшей степени в открытом доступе представлены публикации с исследованием частично заполненных деформируемых конических оболочек [40, 41] . Анализ собственных колебаний свободной
Статья опубликована в открытом доступе по лицензии CC BY 4.0
поверхности жидкости в жёстких усечённых конических оболочках прямой и перевёрнутой форм осуществлён в работах [42 –46] . Детальный обзор публикаций в этой области приведён в [47] . В недавних статьях [48, 49] предложенная постановка позволяет учитывать влияние гравитационных сил, но не подразумевает возможность определения плескательных частот. Насколько известно авторам, только в работе [41] приводятся зависимости плескательных и связанных частот от угла конусности. Заключается, что рост плескательных частот с уменьшением угла при вершине не зависит от геометрических параметров оболочки, а в случае связанных частот имеет место кардинальное различие в поведении коротких и более длинных оболочек. Поскольку эти результаты получены для конкретной комбинации граничных условий, уровня жидкости и номера окружной гармоники, требуется их проверка при других конфигурациях задачи и, в случае подтверждения, обобщение. Именно в этом заключается цель исследования, обсуждаемого в настоящей статье.
Итак, собственные колебания оболочки, частично заполненной жидкостью, на свободной поверхности которой задаётся гравитационное граничное условие, характеризуются появлением плескательных частот, величина которых, как правило, существенно уступает связанным частотам колебаний системы «упругая конструкция–жидкость». При определённой комбинации геометрических и физико-механических параметров, а также условий нагружения плескательные моды становятся сопоставимыми со связанными модами [16] . Это снижает эффективность решения задачи, если её целью является получение и анализ только связанных мод [50] . Для решения этой проблемы в работе [51] был предложен итерационный алгоритм, построенный на основе метода динамической конденсации, который позволяет учитывать эффекты плескания свободной поверхности, но исключать (редуцировать) из общего спектра частот не интересующие моды колебаний. В данной работе процедура редукции будет применяться для идентификации низшей связанной моды колебаний в полном частотном спектре, заранее вычисленном в результате решения стандартной проблемы собственных значений. По мнению авторов, этот затратный в вычислительном плане подход является, тем не менее, более производительным, чем построение и анализ собственных форм колебаний для заранее неизвестной части частотного спектра.
-
2. Постановка задачи
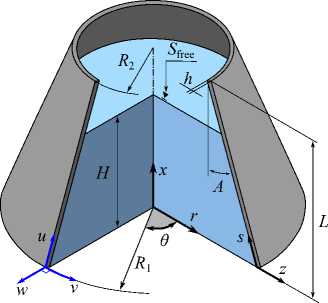
Рис. 1. Усечённая коническая оболочка, частично заполненная жидкостью
-
3. Основные соотношения
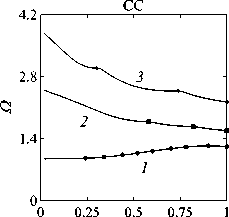
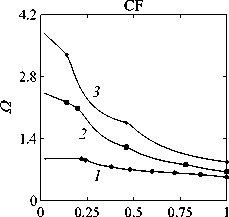
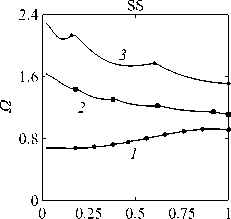
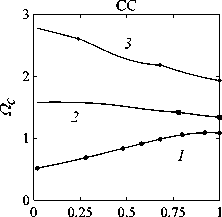
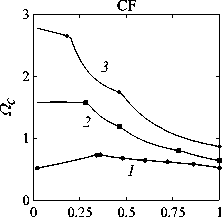
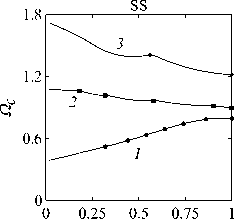
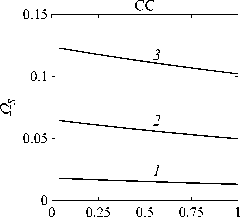
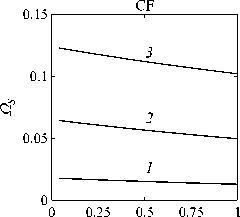
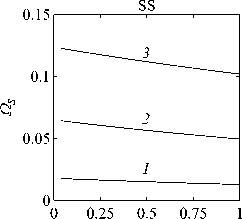
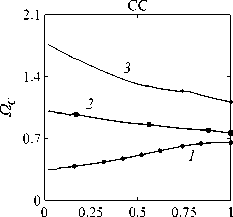
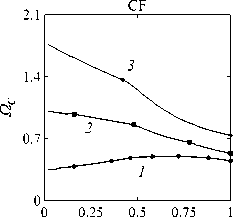
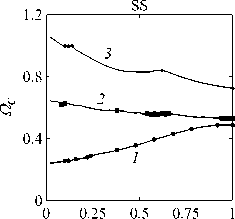
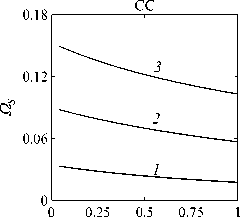
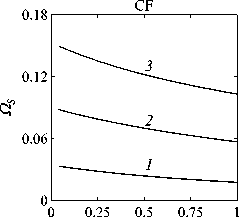
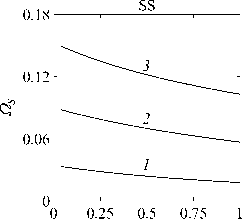
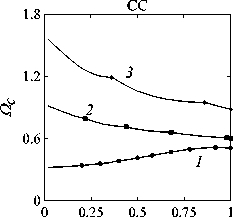
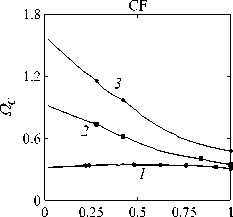
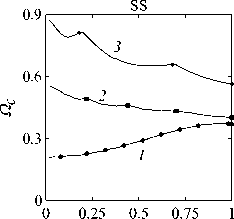
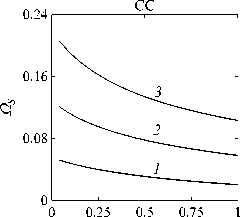
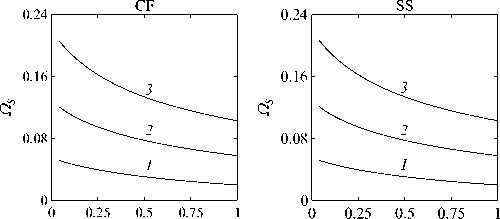
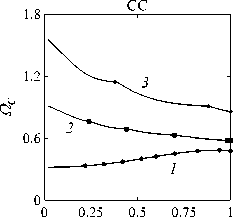
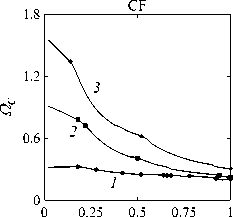
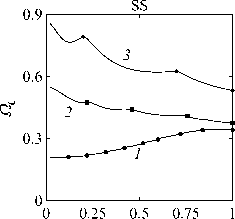
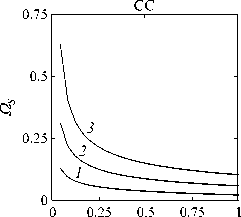
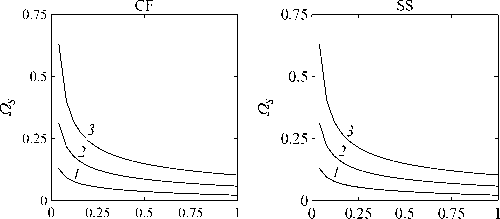
Рассматривается прямая вертикально ориентированная усечённая коническая оболочка вращения (Рис. 1) длиной L, радиусами R1 и R2 , углом при вершине A и толщиной h, частично (на высоту H) заполненная идеальной сжимаемой жидкостью объёмом Vf. На свободной поверхности жидкости Sfree принимаются во внимание эффекты плескания, обусловленные воздействием гравитационного поля. Под конической оболочкой прямой формы понимается оболочка, у которой радиус нижнего конца превышает радиус верхнего. Ставится задача исследования влияния значения угла конусности A на низшие плескательные и связанные частоты колебаний при различных параметрах: отношении L/R1, уровне жидкости H, комбинациях граничных условий, задаваемых на концах упругого тела. При фиксированной высоте оболочки максимально допустимый угол определяется формулой tgA Идеальная сжимаемая жидкость, заполняющая объём Vf , в рамках потенциальной теории описывается волновым уравнением, которое в случае малых возмущений формулируется в виде [52]: 2 д2ф 1 д2ф д2ф 1 дф 1 д2ф ∂r2 r2 ∂θ2 ∂x2 r ∂r c2f ∂t2 , где ф — потенциал скорости, (гДх) — цилиндрические координаты, Cf — скорость звука в жидкости. Потенциал скорости ϕ должен удовлетворять следующим условиям: – на смоченной поверхности Σ £ = Sf nSs : ∂ϕ ∂n ∂u It ^n; – на жёсткой поверхности Здесь Sf иSs — поверхности, ограничивающие объёмы: жидкости — Vf, и оболочки — Vs; u — вектор перемещений оболочки; n — вектор единичной внешней нормали к смоченной поверхности. Давление жидкости pf на смоченной поверхности Σ вычисляется по линеаризованной формуле Бернулли: ∂ϕ pf=-Pf дй’ где ρf — плотность жидкости. Предполагается, что свободная поверхность жидкости Sfree фактически находится на некоторой высоте η относительно своего среднего значения: ∂η ∂ϕ ∂t ∂n . Используя обобщённый вариант уравнения Бернулли Pf+Pf dt+Pfgn=o, из условия на свободной поверхности pf = 0 получим: 1 дф n=-дЭГ где g — ускорение свободного падения. Дифференцируя обе части (5) по времени и подставляя результат в (4), окончательно придём к уравнению плескания свободной поверхности: дф 1 д2ф ∂n g ∂t2 С помощью метода Бубнова–Галёркина волновое уравнение (1) с учётом граничных условий (2), (3) и (6) преобразуем к слабой форме [53]: Л /VFn ^dV + /Fn 4 § c2f∂t2 Vf Vf f du f 1 д2 Ф , -----, dV— J Fn — •ndS + J Fn-dt£dS = 0 (n =1,mf), (7) Σ Sfree где ф и u — пробные решения для потенциала скорости и вектора перемещений оболочки, Fn и mf — базисные функции и их количество. Компоненты Eij вектора деформаций классической теории оболочек, основанной на гипотезах Кирхгофа–Лява, запишем в виде [54]: E11 = £11 + zK11, E22 = ^22 + zK22, E12 = £12 + 2zKi2, £11 = u'+riw, £22 = v* +^u+r2W, £12 = v‘+u* — ^v, К11 = 911 К22 = 9* +^91, К12 = 9* — Ф&2 +r2v, 91 = —w' + r1U, 02 = -W* +r2V, ′ (•••) = 1d(-) A1∂s * 1 д ("') 1A' (•••) A2 д9 ’ ^ A2a2. Здесь (s,9,z) — криволинейные координаты; A1, A2 — коэффициенты Ламе; r1, r2— кривизны; u, v, w — меридиональная, окружная и нормальная составляющие вектора перемещений оболочки u = {u, v, w}T; 91, 92 — углы поворота недеформируемой нормали. Физические соотношения, устанавливающие связь между T — вектором усилий и моментов, и е = {£11,£22,£12,к11 ,к22,2к12}Т — вектором деформаций, представим в матричном виде: T = {T11 ,T22 ,S,M11 M22 M12 }T= De = ab bc ε. Коэффициенты, входящие в матрицу жёсткостей D, определяются по формулам: (aij ,bij ,cij) h/2 = J (Qij(1,z,z2)dz (i,j = 1,2,3), -h/2 Q11 = Q22 = E (-zV2) ’ Q12 = vQ11’ Q33 E Q33 2(1 + v) ’ где E — модуль Юнга, ν — коэффициент Пуассона материала оболочки. Математическую постановку задачи динамики конической оболочки выполним с использованием вариационного принципа возможных перемещений, который с учётом работы сил инерции и соотношений (4) и (8) принимает вид: УSsTDsdS+У psiuTudV — У SuTPdS = 0, Ss Vs Σ где ps — плотность материала оболочки, P = {0,0,pf }T — вектор поверхностной нагрузки. 4. Численная реализация Численная реализация задачи выполнена с помощью полуаналитического варианта метода конечных элементов (МКЭ) [55], основанного на представлении решения в виде ряда Фурье по окружной координате θ: ∞∞ (u,w,^) = X^(uj ,wj ,фj )cosjd, v = ^^Vj sinjO,(10) j=0 где j — номер окружной гармоники. Выразив в (10) искомые переменные через их узловые значения, получили известные матричные соотношения: d = Nde, f = Ffe, e = Bde, где N, F — матрицы функций формы, de, fe — векторы узловых значений для перемещений U и потенциала скорости <ф, B — матрица связи деформаций e с узловыми значениями. Дискретизация оболочки осуществлена высокоточным конечным элементом (КЭ) в виде усечённого конуса с аппроксимацией меридиональной и окружной компонент вектора перемещений кубическим полиномом, а нормальной компоненты — полиномом седьмой степени [56]. Для жидкости использован треугольный КЭ с линейной аппроксимацией потенциала скорости. Стандартные процедуры МКЭ позволили получить из соотношений (7) и (9) с учётом (11) следующую связанную систему уравнений, описывающую взаимодействие оболочки с жидкостью: MX+Cx+Kx = 0, (12) где M= Mf+Mg 0 0 Ms C= 0 ρfCfT -Cfs 0 Kf 0 Ks f d Здесь d, f — векторы обобщённых перемещений и потенциала скорости; точками сверху обозначены производные по времени. Типовые матрицы (масс M, демпфирования C и жёсткости K) для отдельных КЭ сформированы следующим образом: Kf=X/vFTvFdV, Mf=x ДFTFdv, Mg=x у 1 FTFdS, mfVf mfVf f mgSfree Cfs= X / FTNdS, Ks= X / BTDBdS, Ms = X / PsNTNdV. mΣ Σ ms S ms Vs При этом N — функции формы нормальной составляющей вектора перемещений оболочки; ms, mΣ и mg — количество КЭ, на которые разбиты оболочка, а также смоченная и свободная поверхности соответственно. Уравнение (12) переписали в следующем виде: C -I K 0 y + M I У x =0, где y = x, I — единичная матрица. Решение системы (13) искали в экспоненциальной форме: exp(iwt), i = л/—1, где x, y — некоторые функции координат, ш — собственная частота колебаний, i — мнимая единица. С учётом представления (14) систему уравнений (13) свели к стандартной проблеме собственных значений: -M-1C M- 1K У x У x Собственные частоты ω системы (15), вычисление которых осуществлено методом QR-преобразования [57], включают как плескательные, так и связанные моды колебаний. Различие между ними не всегда очевидно. Для идентификации низшей связанной моды в полном частотном спектре использована модификация метода итерационной динамической конденсации, предложенная в работе [51]. Для этого в уравнении (12) с учётом (14) выделили исключаемые (редуцируемые) узловые неизвестные xs, относящиеся к потенциалу скорости жидкости ϕ на свободной поверхности: Mmm Msm Mms Mss +iw c mm sm г ms Css I Kmm K sm Kms Kss После выражения одних переменных через другие из (16) получена следующая система уравнений относительно остальных узловых неизвестных xm [51]: 2 a /Г I • I TZ Л -w2Mxm +iwCxm + Kxm = 0, где M= Mmm + Mms R, “ C=C mm I CmsR, K = Kmm + Kms R, R = -(-w2Mss+i^Css + Kss) 1(-w2Msm+iwCsm+ Ksm). Матрица преобразования R является частотно зависимой, поэтому для решения редуцированной системы (17) необходима итерационная процедура. Такая процедура детально описана в [51]. Поскольку на её каждом шаге отыскивается только одно значение частоты, то эффективность вычислений в большей мере определяется выбором подходящего метода решения частичной проблемы собственных значений. В работе [51] используется метод Арнольди, интегрированный в среду MATLAB. При этом квадратичная проблема собственных значений (17) сводится к обобщённой для несимметричных матриц удвоенной размерности. Реализация этого метода в коммерческой библиотеке программ численного и статистического анализа (International Mathematical and Statistical Library — IMSL) для языка Intel FORTRAN не оптимизирована и не поддерживается многопоточными вычислениями. Кроме этого, согласно [58], в методе Арнольди эффективное нахождение наименьших по модулю собственных значений возможно только в случае применения обратного сдвига, что требует дополнительных матричных операций, приводящих к росту погрешности вычислений. Исходя из сказанного, в настоящей работе процедура итерационной динамической конденсации строилась на основе метода Мюллера [59], который не требует каких-либо избыточных операций с матрицами в (17). Невысокая сходимость метода компенсировалась в данном случае тем, что начальные приближения задавались в окрестности текущего приближения динамической конденсации. 5. Верификация численного алгоритма В связи с отсутствием подходящих для сравнения данных для конических оболочек со свободной поверхностью жидкости верификация численного алгоритма осуществлялась на вертикальной свободно опёртой цилиндрической оболочке, частично заполненной жидкостью, при параметрах оболочки L = 30 м, R = 25 м, h = 0.03 м, H = 21.6 м, E = 2.06 х 1011Па, v = 0.3, ps = 7850 кг/м3, и жидкости: pf = 1000 кг/м3, cf = 1500 м/с. Для указанной конфигурации задачи аналитическое (методом Релея–Ритца) и численное (МКЭ) решения выполнены в работах [16, 51]. В таблице 1 приведены собственные частоты колебаний ω , вычисленные для полной и редуцированной постановок. Здесь m — число полуволн в меридиональном направлении. 6. Результаты расчётов В реализованных численно примерах рассмотрены частично заполненные жидкостью конические оболочки прямой формы (E = 2 х 1011Па, v = 0.3, ps = 7830 кг/м3, h = 0.0254 м), каждый из концов которых или жёстко закреплён (C) u = v = w = 0, dw/ds = 0, или свободно опёрт (S) v = w = 0, или не закреплён (F). В представлении полученных результатов использован безразмерный параметр частоты ^ = ^L (ps/E)0'5х 10-1, у которого нижний индекс «c» соответствует связанной частоте, а индекс «s» — плескательной. Таблица 1 демонстрирует хорошее соответствие результатов, рассчитанных с помощью описанного алгоритма, известным из литературы данным. Процедура итерационной динамической конденсации позволила полностью Таблица 1. Собственные частоты колебаний ω (рад/с) свободно опёртой цилиндрической оболочки, частично заполненной жидкостью (j = 4) Для плескательных частот колебаний верификация проведена на решении для недеформируемой конической оболочки путём сопоставления с данными из [43, 44]. В первой из работ применён численно-аналитический подход, основанный на вариационной схеме Ритца–Треффтца, а во второй использован метод граничных элементов. В вычислениях больший радиус оставался неизменным (R1 = 1 м), а высота столба жидкости определялась как H = (R1 — R2)ctgA, где A = 30 град. В рамках описанного выше алгоритма колебания жидкости в жёсткой оболочке получены при задании C = 0 в выражении (12). В таблице 2 приведены значения безразмерных плескательных частот колебаний а = w2R1 /g, найденные разными методами. По данным из таблицы 2 видно, что КЭ решение хорошо согласуется с данными из других работ. Исключением является вариант с максимальной высотой столба жидкости (R2 = 0.2 м), где различие в результатах самое существенное. Аналогичное поведение с ростом угла конусности выявлено в [60] при решении конечно-элементным и численно-аналитическим методами, но в случае связанных частот. Таблица 2. Плескательные частоты колебаний жидкости σ в жёсткой конической оболочке Источник данных Параметры конической оболочки, [м] R2 =0.2 R2 = 0.4 R2 = 0.6 R2 =0.8 R2 =0.9 j=1,m=1 [43] 11.332 5.629 3.515 1.661 0.726 [44] 11.303 5.626 3.481 1.651 0.732 Расчёт авторов 11.448 5.639 3.517 1.662 0.728 j=2,m=1 [43] 17.760 8.967 5.941 3.724 1.923 [44] 17.939 8.965 5.941 3.726 - Расчёт авторов 18.403 9.001 5.946 3.726 1.927 На рисунке 2 показаны зависимости низших частот колебаний Ω от отношения радиусов ξ пустых оболочек, имеющих различные граничные условия. Графики построены для трёх типоразмеров Z = L/R1, которым отвечают значения радиуса основания конуса R1 = 18,12,6 м. Размеры выбраны произвольным образом и для наглядности ранжированы на графиках по возрастанию ζ через безразмерный параметр. В размерных величинах наибольшее значение частоты соответствует короткой оболочке (Z = 0.67), как самой жёсткой. При повышении значения угла конусности (уменьшении параметра ξ) рост площади боковой поверхности этой оболочки превышает 42% в сравнении с цилиндрической оболочкой радиуса R1 , что привело к снижению частотного спектра. Следует отметить, что для данного значения ζ зависимость частоты от угла конусности для разных комбинаций граничных условий близка к полученной при условии сохранения среднего радиуса (R1 +R2)/2 постоянным и равным радиусу эквивалентной цилиндрической оболочки. В частности, при консольном закреплении CF (нижний конец жёстко ξ Рис. 2. Зависимости безразмерных низших частот колебаний Ω пустой конической оболочки от отношения радиусов ξ для различных значений параметра ζ: 0.67 (кривая 1); 2.0 (2); 5.0 (3), при комбинациях граничных условий C, F, S на концах оболочки закреплён, верхний является свободным), наоборот, имеет место, как и в работах [48, 49], рост низшей частоты, что отражает особенность прямой формы конической оболочки, в отличие от её перевёрнутого аналога (см. в [60]). При двух других типоразмерах рост площади боковой поверхности находится, соответственно, в пределах 6% и 2%, а увеличение частоты обеспечивается благодаря повышению изгибной и крутильной жёсткостей. Изменение жёсткости конструкции, обусловленное геометрией, физико-механическими свойствами материала, внешним воздействием, оказывает влияние не только на спектр собственных частот колебаний, но и на окружную моду, соответствующую низшей частоте. Немонотонный характер кривых, представленных на рисунке 2, хорошо отражает эту особенность. Здесь маркерами отмечены те значения углов при вершине, при которых происходит смена формы колебаний. Волновое число для низшей частоты возрастает с увеличением ограничений на концах конструкции и уменьшается с ростом угла конусности и отношения ζ . В частности, при жёсткой заделке концов (CC) и ζ = 0.67 номер окружной моды последовательно снижается с j = 16 до j = 8, при SS — с 14 до 6. При консольном закреплении (CF) снижение j с 11 до 5 сменяется скачкообразным повышением до 8 при высоких углах конусности A. На рисунке 3 показаны зависимости низших плескательных (Ωs) и связанных (Ωc) частот колебаний от отношения радиусов ξ оболочек, имеющих различные граничные условия. Графики построены для четырёх (а) Рис. 3. Зависимости безразмерных низших связанных Ωc и плескательных Ωs частот колебаний конической оболочки от отношения радиусов ξ для различных значений параметра ζ: 0.67 (кривая 1); 2.0 (2); 5.0 (3), при комбинациях граничных условий C, F, S на концах оболочки; уровень заполнения оболочки ψ: 0.25 (а), 0.5 (б), 0.75 (в), 0.99 (г) ξξξ ξξξ (г) Рис. 3. Продолжение ξξξ ξξξ уровней заполнения ψ = H/L = 0.25, 0.50, 0.75, 0.99 при одних и тех же значениях ζ. Жидкость, находящаяся внутри оболочки, благодаря присоединённой массе, приводит к снижению связанных частот колебаний Ωc , но не оказывает качественного влияния на их зависимости от угла при вершине конуса. Последовательности окружных гармоник, отвечающих низшей частоте, также меняются незначительно. При этом углы конусности, при которых осуществляются переходы от одной формы колебаний к другой, различаются. Сопоставляя графики на рисунке 3 с кривыми для пустых оболочек (Рис. 2), можно сделать следующий вывод: характер изменения связанных частот колебаний от угла конусности в значительной мере зависит как от геометрических параметров оболочки, так и от заданных для неё граничных условий, а вклад жидкой среды является только количественным. Тем не менее, для некоторых конфигураций имеет место исключение, связанное, возможно, с вычислительными аспектами. Так, если при малых уровнях жидкости плескательная и связанная части спектра практически не пересекаются, то с повышением уровня низшая связанная частота становится сопоставимой с одной из плескательных. О таком эффекте сообщается в работе [20]. Процедура редукции даёт погрешность, которая не позволяет однозначно идентифицировать нужную частоту. Вычисления с более мелким шагом приводят к осцилляции нижней частоты, сопровождающейся частым изменением волнового числа. Указанные сложности возникли при анализе свободно опёртой оболочки с уровнем заполнения ψ = 0.5 и ζ=2(Рис.3б). Из зависимостей для частот Ωs, показанных на рисунке 3, видно, что результаты для всех комбинаций граничных условий и любого уровня заполнения являются идентичными, что говорит об отсутствии влияния упругости оболочки на эту часть спектра. Аналогичный вывод сделан в статье [22]. Для всех рассмотренных конфигураций задачи низшей плескательной частоте всегда соответствует первая окружная гармоника (j = 1, балочная мода колебаний), что согласуются с результатами работы [10]. Повышение плескательной частоты тем значительнее, чем выше уровень жидкости даже в случае цилиндрической оболочки, что не совпадает с данными из [12]. Также плескательная частота растёт с повышением угла конусности, что в проведённом исследовании соответствует уменьшению свободной поверхности жидкости. Особенно этот рост существенен при уровне заполнения ф = 0.99. Данные результаты качественно согласуются с графиками, приведёнными в [8]. Численными расчётами также выявлено, что для некоторых конфигураций первая связанная частота для текущей гармоники становится низшей во всём спектре, но, тем не менее, более высокой, чем плескательная при j = 1. 7. Заключение Представлены результаты численного исследования усечённой упругой конической оболочки прямой формы, частично заполненной идеальной сжимаемой жидкостью, описываемой уравнениями потенциальной теории. На свободной поверхности жидкости принимаются во внимание эффекты волнообразования, обусловленные гравитационными силами. С целью повышения вычислительной эффективности идентификация связанных мод колебаний в полном частотном спектре осуществляется с применением итерационной динамической конденсации. Проанализировано поведение плескательных и связанных мод колебаний при различных параметрах задачи: уровнях жидкости в оболочке, углах конусности, линейных размерах оболочек, граничных условиях на их концах. Установлено, что характер зависимостей связанных частот колебаний от угла конусности в большей степени определяется геометрией самой оболочки и заданными для неё кинематическими граничными условиями. Низшая плескательная частота, всегда соответствующая балочной моде колебаний, не зависит от упругих свойств оболочки и повышается как с ростом высоты столба жидкости, так и с уменьшением площади свободной поверхности. Максимальные значения низшей плескательной частоты достигаются при предельных углах конусности и уровне заполнения, близком к полному. Выявлено, что возможны такие комбинации геометрических размеров и уровня жидкости, при которых связанная частота колебаний является низшей во всём спектре, что подчёркивает необходимость принятия во внимание гравитационных эффектов на свободной поверхности при анализе колебательных характеристик системы «оболочка–жидкость». Работа выполнена в рамках государственного задания (регистрационный номер темы 124020700047-3) и Программы создания и развития научного центра мирового уровня «Сверхзвук» на 2020–2025 гг. (реализация метода итерационной динамической конденсации).
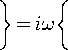
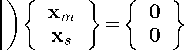
Число полуволн в меридиональном направлении m
Плескательные частоты
Связанные частоты
Источник данных
Источник данных
[16]
[51]
расчёт авторов, полная система
[16]
[51], полная система
[51], редуцир. система
расчёт авторов, полная система
расчёт авторов редуцир. система
1
1.4425
1.4431
1.4428
13.658
14.061
14.061
14.059
14.059
2
1.9081
1.9111
1.9118
34.441
34.614
34.614
34.612
34.612
3
2.2305
2.2382
2.2413
49.692
49.532
49.532
49.553
49.553
4
2.5027
2.5176
2.5245
61.877
61.641
61.641
61.716
61.716
5
2.7444
2.7695
2.7819
71.804
71.793
71.793
71.943
71.943
исключить плескательные моды колебаний: результаты двух расчетов совпадают, но в полной системе плескательные частоты ниже связанных, а в редуцированной — они отсутствуют.