Численное моделирование стационарного течения жидкости в вихревом гидродиоде

Гидравлический диод является проточным элементом, коэффициент гидравлического сопротивления которого существенно различается при прямом и обратном направлении движения жидкости через него. Таким образом, поток жидкости с равным расходом в прямом направлении диода движется при значительно меньшем перепаде давлений на гидродиоде, чем в обратном [1, 2]. Отличительной особенностью гидравлических диодов является отсутствие подвижных элементов в проточной части.

Гидродиоды нашли применение в трубопроводных системах для предотвращения гидравлического удара [3], для ограничения расхода теплоносителя через теплообменники системы вспомогательного охлаждения ядерных реакторов при принудительной циркуляции с обеспечением беспрепятственного течения теплоносителя в противоположном направлении при естественной циркуляции [4, 5], в качестве кавитаторов в системах очистки и обеззараживания воды [6], в качестве органов распределения жидкости в насосах с вытеснителем возвратно-поступательного действия [7–9], а также в различных приложениях в микрофлюидике [10, 11].

Основной характеристикой диода, определяющей его качество, является диодность, которая представляет собой отношение коэффициентов гидравлического сопротивления при движении жидкости в обратном ζоб и в прямом ζпр направлениях:

D = ^Zo6 . (1) ^ζпр

Наиболее перспективным с точки зрения диодности является вихревой диод [12]. Так, существуют исследования, в которых диодность вихревых диодов достигалась более 200 единиц [13].

Разработка новых устройств, включающих в свой состав вихревые гидравлические диоды, требует анализа течения жидкости в проточной части диода в стационарной и нестационарной постановках. При этом следует отметить, что течение жидкости в диоде является сложным, включающим в себя плоские и объемные вихри. Следовательно, применение средств вычислительной гидродинамики для решения задачи анализа течения жидкости в вихревом диоде является обоснованным ввиду комплексности математического описания такого течения. При этом сложность течения жидкости в проточной части диода требует подбора адекватных параметров моделирования, позволяющих с удовлетворительной точностью описать явления, имеющие место быть в потоке.

В работе [14] показано, что использование моделей вихревой вязкости, положительно зарекомендовавших себя для плоских течений, при наличии объемных вихрей дают неудовлетворительный результат. Автор предпринимает попытки усовершенствования двухпараметрических моделей за счет внесения эмпирических поправок корректировки самой турбулентной вязкости. В статье [15] проведено исследование точности и ресурсоемкости различных моделей турбулентности, полученные результаты говорят о том, что с увеличением числа Рейнольдса роль подсеточного моделирования возрастает. В работе [16] авторы приходят к выводу, что успешное применение модели крупных вихрей (LES) требует решения некоторых вопросов, таких как создание методической базы метода LES, определение критериев сходимости и др.

Отсутствие единого подхода к моделированию вихревых течений является проблемой при проектировании вихревых диодов. Авторы используют различные модели турбулентности, настройки сетки и критерии сходимости. Так, в работе [17] Kulkarni и др. проводят серию расчетов вихревых диодов, пренебрегая напряжениями Рейнольдса и учитывая только молекулярную вязкость, верифицируя свой подход путем сравнения результатов моделирования с экспериментальными данными [18]. При этом в первом приближении авторы используют модель турбулентности k-s, однако полученные результаты не показывают удовлетворительной сходимости с экспериментом. Цветков и др. [19] моделируют в ANSYS диод повышенной диодности при помощи модели вихревой вязкости SST, а Yin и др. в своей работе [20] описывают моделирование вихревого диода с помощью модели больших вихрей LES. В работе [21] Pandare и др. используют для численного моделирования вихревого диода модель турбулентности SST. В работах [22] и [13] авторы используют модель турбулентности RSM.

Аналитический обзор научно-технической литературы показывает, что в настоящее время отсутствует единый подход к моделированию течения жидкости в проточной части вихревого гидравлического диода. Это затрудняет применение численного моделирования при постановке численных экспериментов, направленных на исследования вихревых диодов.

Данная работа направлена на определение оптимальных параметров численного моделирования, применение которых при постановке численного эксперимента позволяет получить результаты удовлетворительной точности.

Для решения поставленной задачи проведена серия численных экспериментов с применением ряда моделей турбулентности, адекватность которых оценивалась путем сопоставления результатов численного моделирования и физического эксперимента.

В качестве объекта исследования выбран вихревой гидравлический диод, профиль и размеры проточной части которого описаны в статье [17].

В данном исследовании рассмотрены четыре наиболее часто используемые при моделировании течений в вихревых диодах математические модели турбулентности. В результате каждого численного эксперимента были определены зависимости перепадов статических давлений на гидродиоде в прямом и обратном направлении и основная характеристика диода - зависимость диодности от числа Рейнольдса.

С целью проверки адекватности применения выбранных для исследования моделей турбулентности проведен физический эксперимент, в результате которого получены зависимости пе- репадов давлений в прямом и обратном направлении диода от расхода, а также зависимость ди-одности от числа Рейнольдса

Верификация численной модели осуществлялась методом сравнения результатов численного моделирования и физического эксперимента.

Материалы и методы

Геометрическая модель исследуемого вихревого диода представлена на рис. 1.

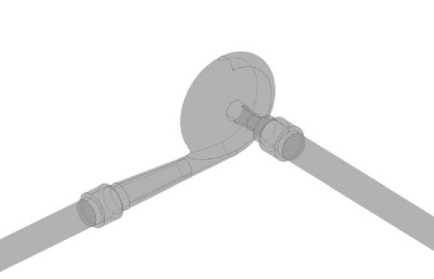
Рис. 1. Модель проточной части диода

Fig. 1. The model of the flow part of the diode

Для проведения численного эксперимента в данной работе использовались следующие модели турбулентности: k-ε, SST, RSM. Также использовалась ламинарная модель. Модели k-ε, SST, RSM относятся к методу, основанному на осреднении по Рейнольдсу уравнений Навье–Стокса (Reynolds averaged Navie–Stokes или RANS). Модель k-ε является двухпараметрической моделью, в которой турбулентная вязкость высчитывается путем решения двух дополнительных уравнений: кинетической энергии турбулентности k и скорости диссипации турбулентности ε. Данная модель позволяет рассчитывать турбулентные течения с приемлемой точностью, однако при моделировании отрывных течений точность расчетов оказывается низкой.

Модель SST сочетает в себе модели k-ε и k-ω. Для расчета течения свободного потока используются уравнения k-ε, а для расчета потока вблизи стенок – уравнения k-ω. Модель SST хорошо показывает себя в расчетах отрывных течений с небольшой зоной отрыва.

Модель RSM основана на уравнениях переноса компонентов тензора напряжений Рейнольдса и скоростей диссипации. Эти модели основаны не на гипотезе вихревой вязкости, а решают уравнения переноса напряжений Рейнольдса в жидкости. Уравнения переноса модели RSM решаются для компонентов напряжения по отдельности. Модели RSM хорошо описывают эффекты кривизны линий тока, внезапных изменений скорости (например, интенсивные вихревые потоки) по сравнению с моделями вихревой вязкости.

При моделировании ламинарных течений используется ламинарная модель и движение потока полностью описывается уравнениями RANS. Обычно условием применения ламинарной модели является низкое число Рейнольдса (Re < 1000). Передача энергии в жидкости в этом случае осуществляется молекулярным взаимодействием. В данной работе использование ламинарной модели связано с рекомендациями, приведенными в статье [17], в которой авторы аргументируют ее выбор ламиниризирующей структурой потока внутри вихревой камеры, однако отмечают некачественное описание течения в тангенциальном и осевом соплах диода.

Помимо модели турбулентности существенное влияние на результат моделирования оказывает значение шага по времени. Высокое значение шага по времени негативно повлияет на точность результатов моделирования, однако использование слишком малого значения шага приведет к чрезмерно высокому времени расчета. Оптимальные значения шага по времени для каждой из используемых моделей турбулентности определялись итерационным методом.

Также на точность расчетов оказывает влияние сетка. Для определения оптимального количества элементов сетки для каждой из используемых моделей турбулентности был проведен анализ сеточной сходимости. Результаты для модели турбулентности RSM в виде графика приведены на рис. 2. В результате анализа сеточной сходимости стало ясно, что для моделей k-ε и ламинарной может быть использована одна сетка, так же как и для моделей SST и RSM. Сетки, используемые для моделей k-ε и ламинарной, для моделей SST и RSM приведены на рис. 3 и 4 соответственно. Сетки состоят из тетраэдрических элементов с призматическим приграничным слоем.

Параметры моделирования при проведении численных экспериментов приведены в таблице.

На рис. 5 приведены поля скоростей для каждой из моделей в прямом направлении, а на рис. 6 – в обратном.

D

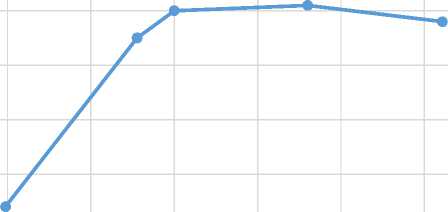
Кол-во эл-в, млн. шт.

Рис. 2. Результат анализа сеточной сходимости для модели турбулентности RSM

Fig. 2. The result of the grid convergence analysis for the RSM

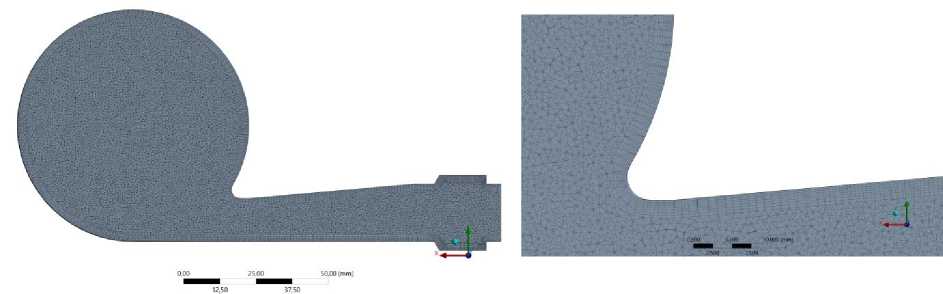
Рис. 3. Сетка, используемая при численном моделировании с моделью турбулентности k-ε и ламинарной моделью

Fig. 3. The grid used in numerical simulation with the k-ε turbulence model and the laminar model

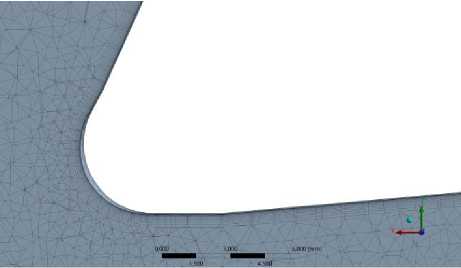
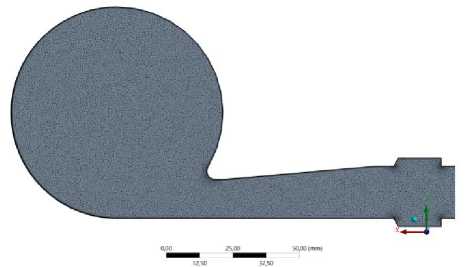
Рис. 4. Сетка, используемая при численном моделировании с моделями турбулентности SST и RSM Fig. 4. The grid used in numerical simulations with SST and RSM turbulence models

Параметры численных экспериментов Parameters of numerical experiments

Модель турбулентности	Шаг по времени (явный/мнимый), с	Количество элементов, млн	Размер первого пристеночного элемента, мм	Время счета одной расчетной точки, ч
Laminar	0,005	1,8	0,2	0,3
k-ε	0,002	1,8	0,2	0,5
SST	0,0001	3,2	0,005	2
RSM	0,00005	3,2	0,005	3

На рис. 7 приведены поля давлений при движении потока жидкости в прямом направлении, а на рис. 8 – в обратном.

Для проверки адекватности результатов численного моделирования был поставлен физический эксперимент. Испытательный стенд показан на рис. 9, его принципиальная схема – на рис. 10. Центробежный насос Н (см. рис. 10) осуществлял подачу воды на испытываемый гидравлический диод ГД. Регулирование расхода воды осуществлялось регулируемым дросселем Д. Расход жидкости измерялся с помощью мерной емкости ЕМ. Перепады давлений на гидравлическом диоде измерялись с помощью манометра МН1, малые перепады измерялись с помощью U-образного дифференциального манометра МН2.

В качестве контрольно-измерительного оборудования использовались:

– манометр стрелочный (10 бар, класс точности 0,4);

• –    манометр U-образный (длина 1,5 м);

• –    мерная емкость и секундомер для измерения расхода.

  

  а)

  
  
  
  
  
  

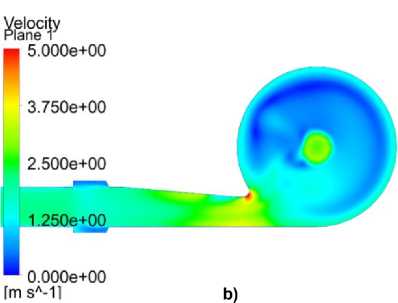
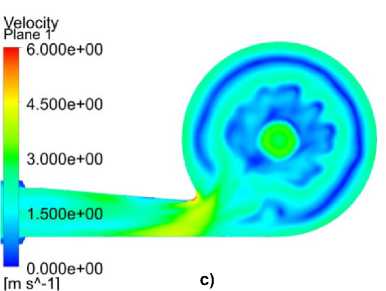
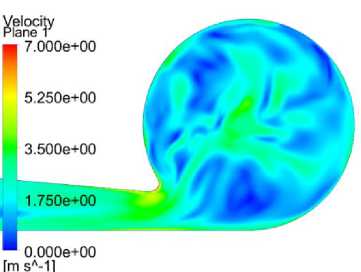
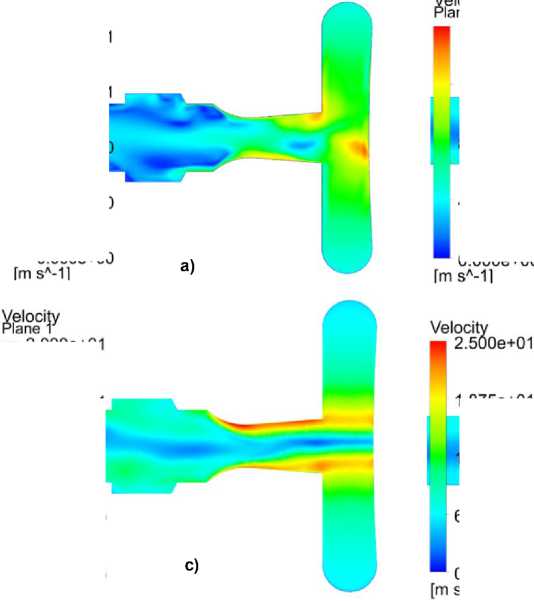
  Рис. 5. Поля скоростей в прямом направлении: а) ламинарная модель;

  b) модель k-ε; c) модель SST; d) модель RSM

  Fig. 5. Velocity fields in the forward direction: a) laminar model;

  b) k-ε model; c) SST model; d) RSM

  
  
  
  
  

  1.600e+01

  1.200e+01

  8.000e+00

  8.500e+00

  4.000e+00

  4.250e+00

  0.000e+00

  0.000e+00

  1.275e+01

  У» ■ 1.700e+01

  

  2.000e+01

  1.875e+01

  1.500e+01

  1.250e+01

  1.000e+01

  6.250e+00

  5.000e+00

  0.000e+00

  S^A-1]

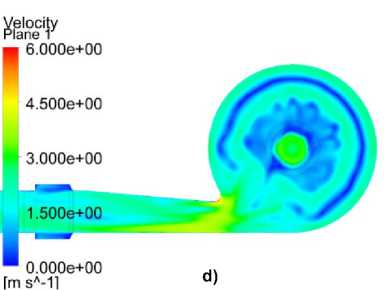
  Рис. 6. Поля скоростей в обратном направлении: а) ламинарная модель; b) модель k-ε;

  c) модель SST; d) модель RSM

  Fig. 6. Velocity fields in the opposite direction: a) laminar model; b) k-ε model; c) SST model; d) RSM

  0.000e+00 [m s^A-1l

  
  

  b)

  
  

  d)

  
  

  1,088e+04

  9.000e+03

  7.2506+03

  б.ОООе+ОЗ

  Total Pressure Plane 1

  1,450e+04

  Total Pressure

  Plane 1

  ■ 1.200e+04

  

  0.000e+00

  1 125e+04

  1.125e+04

  7.500e+03

  7.500e+03

  3.7506+03

  3.750e+03

  0.000e+00

  0.000e+00 [Pal

  Total Pressure

  Plane 1 ■ 1.500e+04

  Рис. 7. Поля давлений в прямом направлении: а) ламинарная модель; b) модель k-ε;

  c) модель SST; d) модель RSM

  Fig. 7. Pressure fields in the forward direction: a) laminar model; b) k-ε model; c) SST model; d) RSM

  ¹¹ 0.000e+00 [Pal

  
  

  Total Pressure

  Plane 1

  ■r 1.500e+04

  
  

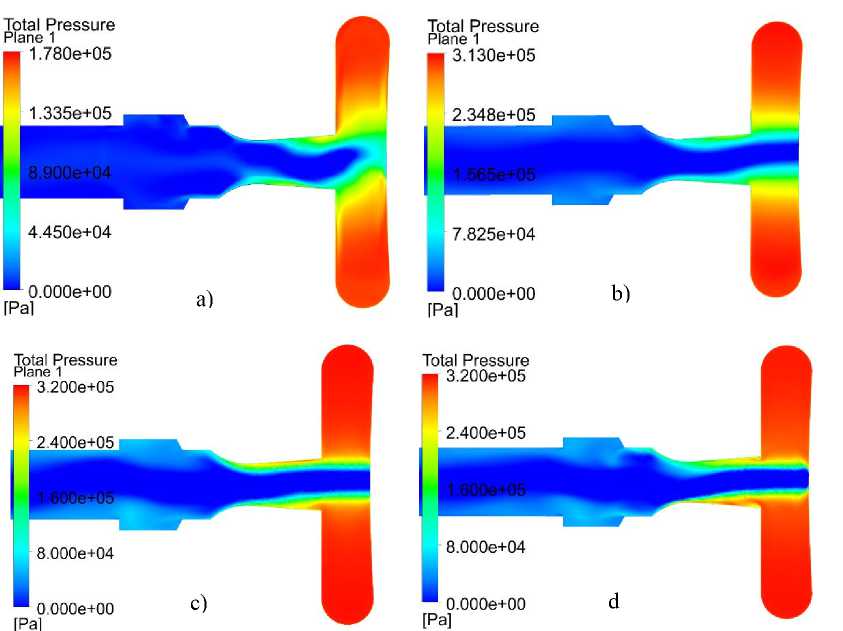
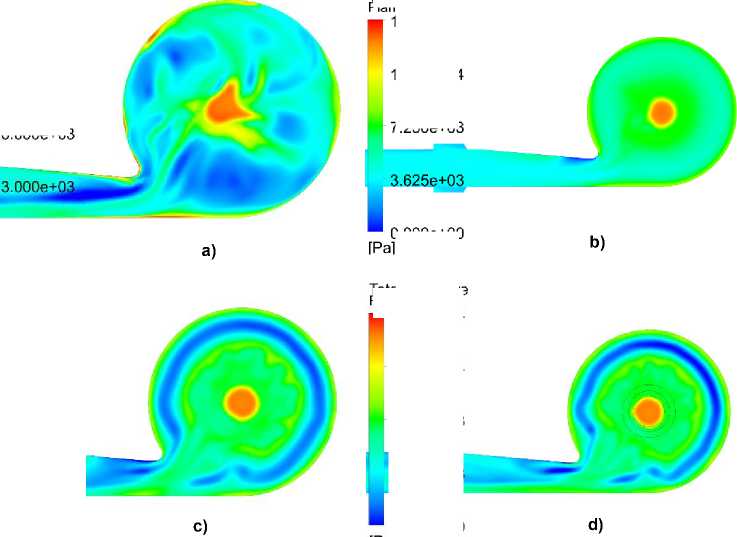
Рис. 8. Поля давлений в обратном направлении: а) ламинарная модель; b) модель k-ε;

c) модель SST; d) модель RSM Fig. 8. Pressure fields in the opposite direction: a) laminar model; b) k-ε model; c) SST model; d) RSM

Рис. 9. Стенд испытательный

Fig. 9. The test bench

Геометрические параметры испытываемого гидравлического диода были аналогичны параметрам, которые использовались при численных экспериментах. Диод был изготовлен методом 3D-печати с подготовкой внутренней поверхности проточной части для достижения минимальной ее шероховатости.

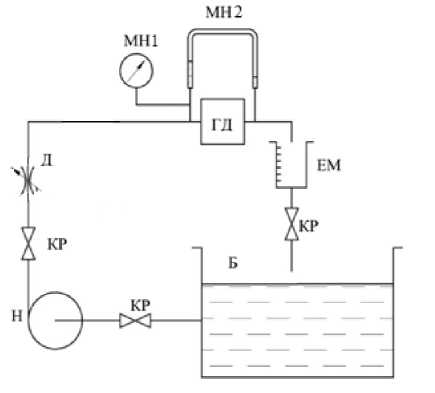
Рис. 10. Принципиальная схема испытательного стенда

Fig. 10. Schematic diagram of the test bench

Исследование проводилось в два этапа. На первом этапе испытываемый диод проливался в направлении, соответствующем наибольшему гидравлическому сопротивлению (обратном направлении). Напорная линия насоса была подключена к тангенциальному соплу гидравлического диода, а осевое сопло соединено со сливной линией, которая сообщается с атмосферой. Дроссель Д в начале эксперимента был полностью закрыт. Постепенно открывая проходное сечение дросселя, задавался перепад давлений на гидродиоде. При этом давление на входе в гидравлический диод регистрировалось при помощи манометра МН1 или U-образного манометра МН2, давление на выходе диода принималось равным атмосферному. При каждой настройке дросселя измерялся расход жидкости через гидродиод объемным способом.

На втором этапе эксперимента напорная линия насоса была подключена к осевому соплу гидравлического диода, а тангенциальный выход подключен к сливной линии, сообщающейся с атмосферой (прямое направление). Методика испытаний аналогична первому этапу.

Замеры для каждой из точек проводились не менее шести раз.

Результаты и обсуждения

В результате проведения численного моделирования и экспериментального исследования гидравлического диода были получены зависимости перепадов давлений на соплах гидравлического диода при прохождении потока жидкости в прямом и обратном направлениях от расхода жидкости. Графики зависимостей для численных и реального экспериментов приведены на рис. 11 и 12 в прямом и обратном направлениях соответственно. При этом для наглядного сравнения на данные физического эксперимента нанесены пределы погрешности 5 %.

Др, Па

0 0,0      5,0

• Эксперимент

--к-е

10,0     15,0

- SST

---RSM

а)

‘IW*

20,0     25,0     30.0     35,0

Ламинарная модель Q> л/мин

---Эксперимент

- -к-е

- SST

---RSM

30000     40000     50000

Ламинарная модель ^с

b)

Рис. 11. Сравнение зависимостей, полученных в результате численного моделирования и физического эксперимента, для прямого направления диода: а) зависимость перепада давлений на диоде от расхода; b) зависимость коэффициента гидравлического сопротивления от числа Рейнольдса

Fig. 11. Comparison of dependencies obtained as a result of numerical modeling and physical experiment for the forward direction of the diode: a) dependence of the pressure drop on the diode on the flow rate;

• b) dependence of the hydraulic resistance coefficient on the Reynolds number

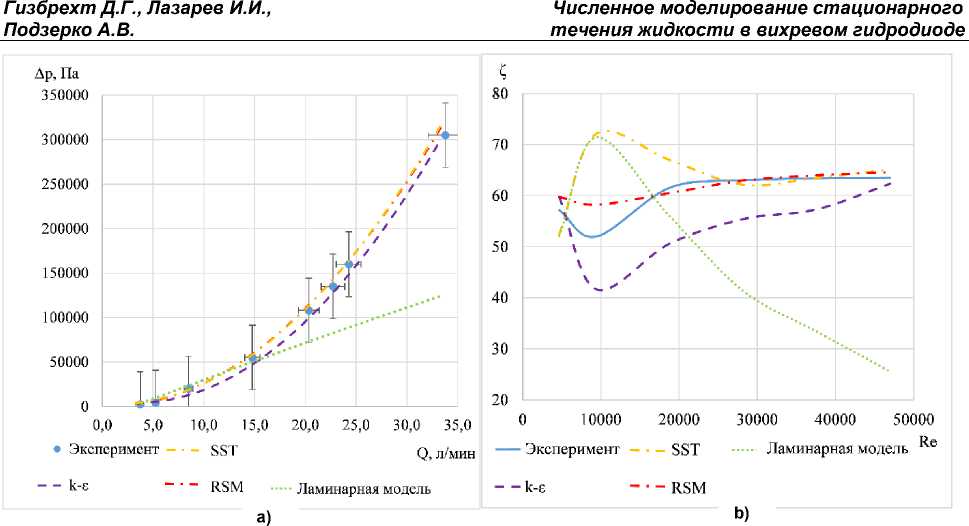
Рис. 12. Сравнение зависимостей, полученных в результате численного моделирования и физического эксперимента, для обратного направления диода: а) зависимость перепада давлений на диоде от расхода; b) зависимость коэффициента гидравлического сопротивления от числа Рейнольдса

Fig. 12. Comparison of dependencies obtained as a result of numerical modeling and physical experiment for the reverse direction of the diode: a) dependence of the pressure drop on the diode on the flow rate;

b) dependence of the hydraulic resistance coefficient on the Reynolds number

По результатам численного моделирования и физического эксперимента рассчитана зависимость диодности исследуемого гидродиода от числа Рейнольдса, которая показана на рис. 13. При этом число Рейнольдса рассчитывалось по параметрам в поперечном сечении тангенциального сопла с наибольшим диаметром (входное сечение тангенциального сопла).

Как видно из рис. 11а и 11b, только модель турбулентности RSM описывает течение в прямом направлении диода с удовлетворительной точностью во всем диапазоне исследованных величин расхода и числа Рейнольдса. При этом модель ламинарного течения дает наименее точные результаты расчета и, как видно из рис. 5а, не позволяет получить качественного описания гидродинамической картины течения в прямом направлении диода при высоких значениях расхода жидкости. Модели турбулентности SST и k-ε применимы для моделирования потока жидкости в прямом направлении вихревого диода в области больших чисел Рейнольдса и позволяют получить точность результатов расчетов выше, чем при использовании RSM модели в этой области. Однако с уменьшением расходов и чисел Рейнольдса точность расчетов с применением моделей SST и k-ε снижается.

Данные на рис. 12а и 12b показывают, что модель турбулентности RSM также описывает течение в обратном направлении вихревого диода с удовлетворительной точностью во всем диапазоне исследованных величин расхода и числа Рейнольдса. При этом ламинарная модель и в обратном направлении диода не дает качественного описания течения, что также подтверждается гидродинамической картиной потока, показанной на рис. 6а. Модель турбулентности SST с удовлетворительной точностью позволяет моделировать течение жидкости в обратном направлении диода при больших расходах и числах Рейнольдса, а с их уменьшением точность моделирования снижается. Модель k-ε является наименее перспективной для использования в численном моделирования обратного потока в вихревом диоде ввиду сравнительно низкой точности результатов моделирования во всем исследуемом диапазоне чисел Рейнольдса.

Анализ кривых на рис. 13 показывает, что применение модели турбулентности RSM при моделировании потоков в прямом и обратном направлениях вихревого диода позволяет рассчитать диодность по сопротивлению с наибольшей точностью по сравнению с другими моделями. При больших числах Рейнольдса модель SST показывает сопоставимые результаты расчета с результатами, полученными по модели RSM при моделировании потоков в обоих направлениях.

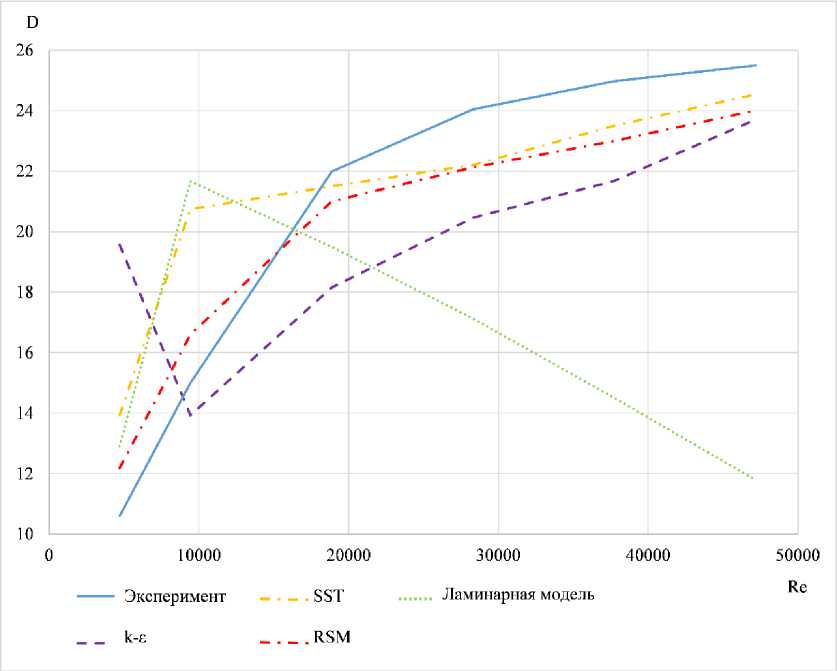
Рис. 13. Графики зависимости диодности от числа Рейнольдса

Fig. 13. The dependence of diodicity on the Reynolds number

Таким образом, использование модели турбулентности RSM позволяет моделировать течение жидкости в проточной части вихревого диода с высокой, по сравнению с другими рассмотренными моделями, точностью. Однако ввиду ее относительно высокой ресурсоемкости для предварительных расчетов видится оптимальным применение модели SST.