Численное моделирование t-напряжений и коэффициента биаксиальности напряжений для образца с центральной трещиной при смешанных граничных условиях

Анализ напряженно-деформированного состояния в окрестности трещин является важной составляющей в современном подходе при оценке прочности, трещиностойкости и ресурса высоконапряженных элементов конструкций. Информация о напряженном состоянии вблизи трещины позволяет обоснованно изучить закономерности ее развития, определить предельные нагрузки, произвести расчет статической и усталостной прочности и на основании этого обеспечить безопасную и безаварийную работу инженерных конструкций.

Достаточно продолжительное время в линейной механике разрушения упругого тела учитывалась лишь сингулярная составляющая поля напряжений у вершины трещины, при этом мерой сингулярности служил обычно коэффициент интенсивности напряжений (КИН), однако многочисленные теоретические и экспериментальные исследования показали необходимость введения дополнительного параметра в целях уточнения однопараметрического подхода. Вследствие этого в последние годы интенсивно развивается так называемая двухпараметрическая модель механики разрушения. Оказалось, что многие противоречия будут устранены, если в разложении Вильямса [1] сохранить второй — несингулярный — член. Этот член называют Т-напряжением. Наряду с ним при двухпараметрическом подходе для оценки параметров жесткости напряженного состояния у вершины трещины широко используется безразмерный коэффициент биаксиальности [2]:

B=

T π a

K

T

F σ ^.

Здесь: a — длина трещины; σ — напряжение, приложенное к образцу при одноосном растяжении; K и F — размерный КИН и КИН, нормированный на величину σπ a . Параметр B можно рассматривать как меру стеснения деформаций в зоне предразрушения у вершины трещины. Заметим, что для представляющих интерес в исследованиях вязкого разрушения образцов параметр биаксиальности табулирован и представлен в виде графиков при разной геометрии и различных схемах нагружения [2, 3]. Вероятно, первой работой, в которой большое внимание уделено включению второго (или первого несингулярного) члена, была работа Ларссона и Карлссона [4]. После публикаций [5, 6] двухпараметрическое представление стало распространенным в расчетах механики разрушений. Для оценки Т- напряжений применяются разные методы, чаще всего метод конечных элементов (МКЭ) и метод граничных элементов.

В обзорной статье [7] достаточно подробно обосновывается необходимость учета влияния Т- напряжений при определении траектории развития трещины, при оценке усталостной долговечности конструкций, а также при выявлении формы и размеров пластических зон и параметров локального стеснения деформаций в окрестности вершины трещины. Различные аспекты значимости Т- напряжений в двухпараметрической механике разрушения рассматриваются в работах Ю.Г. Матвиенко и его коллег [8–10]. В рамках такого подхода, в частности, показано, как важно принимать во внимание несингулярные компоненты поля напряжений в критериальных задачах механики разрушения [8, 9], в расчетах размера и формы зон пластической деформации в окрестности вершины трещины [10]. В работе [11] дается оценка точности расчетов Т -напряжений в зависимости от погрешностей, возникающих при экспериментальном или численном моделировании. Установлено, что метод разложения по собственным функциям Вильямса позволяет обеспечить достаточную для практических целей точность вычисления несингулярных напряжений, даже если исходные данные содержат значительные погрешности. В [12] предложен метод, который можно назвать экспериментально-аналитическим: коэффициенты в разложении Вильямса рассчитываются по экспериментально найденным значениям перемещений заданных в образце точек. Задача решается на основе минимизации невязки между теоретическими и экспериментальными величинами перемещений.

Заметим, что интерес к различным аспектам влияния Т- напряжений из полного решения Вильямса не ослабевает [13–20]. Так, в недавно опубликованных работах [13, 18] проведено экспериментальное и теоретическое прогнозирование распространения и роста усталостной трещины в различных образцах, а статьи [19, 20] посвящены разработке критериев для прогнозирования разрушения материалов с трещинами, в том числе обладающих свойствами ортотропии. Таким образом, исследования по расчету и применению Т- напряжений продолжают интенсивно развиваться, что подчеркивает актуальность данного направления. Предлагаемый в данной статье подход основан на сочетании как аналитических результатов, состоящих в асимптотическом представлении компонент напряжений и перемещений, так и численных расчетов при оценке искомых коэффициентов в этих разложениях.

Цель настоящей работы заключается в применении графового метода при математическом моделировании напряженно-деформированного состояния в окрестности вершины трещины и введении на основе вычислительного эксперимента параметров для оценки Т- напряжения и коэффициента биаксиальности в пластине с центральной трещиной.

2.    Метод численного расчета

В данной работе поля деформаций и напряжений находятся нестандартным численным методом, в котором сплошное тело с помощью ориентированных графов представляется в виде дискретной модели [21–26]. Для расчета напряженно-деформированного состояния в окрестности особых точек разреза, вблизи остроконечных включений и других сингулярных точек и линий в [27] автором предложен специальный сингулярный элемент. В предположении сингулярного характера распределения напряжений и деформаций у вершины трещины неизвестные деформации в пределах элемента аппроксимируются выражениями, содержащими как линейные полиномы относительно переменных x и y , так и сингулярный член с особенностью типа r ^{- 0,5}, которая присуща чисто упругим решениям [3]. Именно такой сингулярный элемент используется в расчетах, результаты которых обсуждаются в данной статье.

3.    Оценка Т-напряжений и коэффициента биаксиальности

Компоненты напряжений и перемещений вблизи вершины трещины с учетом второго члена в разложении Вильямса для задачи о трещине нормального отрыва имеют вид [1, 5]:

^ст xx

K

cos

V 2 n r   2

1 — sin ^ sin ^ j + T + O (^) ,

^ст yy

K

9 Л . • 9 • 39) .

cos — 1 + Sin — Sin — + O rr ,

2 1         2     2 J '    ²

K xy     2n r

9.9     39     /    \ cos —sin —cos — + O (sir ) ,

U y

U x

—

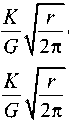
T ( к + 1 ) /

+—-^—-( r cos 9 + a ) + O ( r V r ) ,

, 9) T(к — 3)            /   - cos2— +—------r sin9 + OIrVr ).

2 J       8 G                '     ’

Здесь: K — КИН в условиях нормального отрыва; ( х , у ) и ( r , 9 ) — декартовы и полярные координаты с началом (полюсом) в вершине трещины соответственно; к — параметр, характеризующий тип напряженного состояния ( к = 3 — 4v — для плоского деформированного состояния, к = ( 3 — v )/( 1 + v) — для плоского напряженного состояния); G и v — модуль сдвига и коэффициент Пуассона материала.

В вычислительном аспекте важным является способ нахождения Т-напряжений через компоненты или напряжений, или перемещений, определенные в узлах конечно-элементной сетки. Для расчета Т-напряжений существует несколько подходов [7, 17]. Можно воспользоваться компонентой ста . Так, если рассматривать берега трещины, когда 9 = —п или 9 = п, то из формулы (1) последует: T = ст„„. Если исходить из значения ст^ на верхней и нижней поверхностях трещины при 9 = ±п, то Т-напряжения найдутся по формуле: T =1 [(стxx ^ + (стxx ^].

Применив метод напряжений, из формул (1), (2) определим Т-напряжения через компоненты действующих напряжений на продолжении трещины при 9 = 0 :

T = (ст —ст )    .

\ xx     УУ /9= 0

Альтернативным подходом является вычисление Т -напряжений на основе перемещений. Выражение для расчета Т -напряжений методом перемещений следует из формулы (3) после несложных преобразований:

_т= 8G U x ( 0 ) — U x ( x )

к +1       r где Ux (x) — перемещения вдоль оси Ох точек берега трещины, расположенных на расстоянии r от вершины, Ux (0) — перемещение вершины трещины вдоль оси Ох .

В процессе численного анализа Т -напряжения, в отличие от теоретических значений, не остаются постоянными. Они зависят от метода расчета, от степени разреженности конечно-элементной сетки, от расстояния до вершины трещины. В связи с этим в данной работе предлагается брать в расчет средние значения Т -напряжений, определенные в n точках вдоль берега трещины или на ее продолжении. Так, при расчете с помощью формулы T = ст_хх для среднего значения можно ввести выражение:

n

T = - Уст J x ) .

S              xx i n i=1

Точно так же на основании формул (4), (5) получим следующие средние значения для Т -напряжений, записанные через компоненты напряжений и перемещений соответственно:

1 ⁿ

TSS     XlCxx (x )  Cyy (x)) ,

n , = 1

T D = 1y G i ( U x ( 0 ) - U x ( x )) / r ■ n ^{K +} 1 _Z =1                       /

Расчет средних значений Т -напряжений проведем на одной из модельных задач теории трещин — задаче о равномерном растяжении квадратной пластины с поперечной центральной трещиной. При нагружении пластины трещина раскрывается, а вершины трещины в процессе деформации перемещаются. Эта информация может быть использована для оценки параметров жесткости напряженного состояния у вершины трещины. Поэтому, наряду со средними Т -напряжениями для описания состояния образца с трещиной предлагается вводить величину Р = А UE, ( а с ) , где A U — перемещение вершины при раскрытии трещины (оно легко определяется из натурного эксперимента), E — модуль упругости материала пластины, с — напряжение, приложенное к краям пластины с координатами у = ± H, а — полудлина трещины. При натурных измерениях можно применить, например, методы корреляции цифровых изображений или электронной цифровой спекл-интерферометрии. Они, как отмечается в [12], обеспечивают возможность получения практически неограниченных объемов экспериментальной информации в виде полей перемещений в зонах трещин. Кроме параметра р , будем рассматривать также безразмерные параметры

Т

^T SS

Р SS        ’

Т T _D

Р DD       ’

с

которые в приведенном ниже вычислительном с параметром р .

эксперименте сравним как

между собой, так и

4.    Результаты численного эксперимента

В представленных ниже численных расчетах при оценке Т -напряжений и коэффициента биаксиальности применяется комбинированный подход, основанный на использовании формул (6) и (7). ассматривается квадратная пластина с центральной трещиной, перпендикулярной оси O y , при одноосном равномерном растяжении (Рис.). Ее характеристики: модуль упругости E = 10000 МПа, коэффициент Пуассона v = 0,3, ширина 2 w = 240 мм, высота 2 H = 240 мм, длина 2 а . Граничные условия формулируются следующим образом: полагается U_x = 0 при x = 0; U = 0 при у = 0 вне разреза; берега трещины свободны от напряжений. На сторонах пластины, параллельных трещине, действуют постоянные растягивающие напряжения интенсивностью с = 100 МПа. На части боковых сторон пластины, параллельных оси O y , приняты условия жесткого защемления: U_x = 0, U_y = 0

(на рисунке места защемления выделены жирными линиями), оставшиеся части боковых границ свободны от напряжений. Такие граничные условия могут иметь место в задаче об усилении пластины с трещиной с помощью тонкого упругого покрытия или стрингера. Конечно, здесь изучается не реальная конструкция, а ее идеализированная модель, однако граничные условия на боковой грани при EJE >> 1 будут выполнены приближенно, а условия защемления реализуются при Ex ^ м, где Ех — модуль упругости подкрепляющего элемента.

Изучается плоское напряженное состояние пластины. Ввиду симметрии рассматривается четверть расчетной области (на рисунке она заштрихована). Исследуемая область разбивается на 480 прямоугольных элементов. В окрестности вершины трещины в качестве концевых используются 2 сингулярных (графовых) элемента размером 0,4х0,2 мм. Во всех других элементах применяется линейная аппроксимация деформаций. При определении средних значений Т-напряжения вычисляются в n точках вдоль берега трещины (или на ее продолжении) на участке длиной d = 0,2a , отсчитываемом от вершины трещины. Шаг разбиения во всех расчетах равняется 0,2 мм.

Пример 1. С целью верификации подхода рассмотрим сначала одноосно растягиваемую квадратную пластину с трещиной при отсутствии закрепления на боковых сторонах ( h = 0). Расчеты проведем в зависимости от отношения длины трещины 2 a к ширине пластины 2 w (см. Рис.). В таблице 1 приведены значения параметра β , безразмерных параметров, вычисленных по формулам (6)–(8), а также даются в сравнении расчетные данные. Представленные результаты показывают, что при h = 0 параметр в близок по величине к значениям параметров в« = T_ss /ст , P_DD = T_D /ст . Максимальная погрешность в методе напряжений составляет примерно 1%, а в методе перемещений она не превосходит 4%. Значимость параметра β в том, что эта характеристика легко может быть найдена из натурного эксперимента на основании только одного замера.

Таблица 1. Сравнение безразмерных Т- напряжений (в₅₅ , в^_D ) с параметром в

aw Параметр	0,2	0,3	0,4	0,5	0,6	0,7	0,8
β	-1,052	-1,151	-1,288	-1,444	-1,669	-1,975	-2,381
в	-1,039	-1,137	-1,275	-1,451	-1,672	-1,960	-2,357
в ЗУ в	0,988	0,988	0,989	1,005	1,002	0,992	0,989
в DD	-1,031	-1,130	-1,258	-1,403	-1,604	-1,891	-2,345
в DD в	0,980	0,982	0,977	0,972	0,961	0,957	0,985
в ЗУ в DD	1,008	1,006	1,014	1,034	1,042	1,036	1,005

Оценим безразмерный параметр В_ех = в/ F . Значения безразмерного КИН — F , при различных отношениях aw взяты из работы [27]. Они вычислены с помощью энергетического инвариантного интеграла Черепанова–Райса и хорошо согласуются с результатами, полученными Исидой с помощью рядов Лорана [27, 30]. В таблице 2 представлены в сравнении экспериментальный — В , и теоретический — В , параметры биаксиальности для случая одноосно растягиваемой пластины при H = w . Участвующие в расчетах значения в взяты из таблицы 1. В качестве параметра биаксиальности, который будем считать теоретическим, для квадратной пластины примем величину, найденную по формуле: B t = - ( 1 + 0,085 k ) [21]. Здесь Х = a/w .

Таблица 2. Сравнение безразмерных параметров биаксиальности при одноосном растяжении квадратной пластины

aw Параметр	0,2	0,3	0,4	0,5	0,6	0,7
B ex	-0,997	-1,025	-1,040	-1,064	-1,101	-1,146
B t	-1,017	-1,025	-1,034	-1,043	-1,051	-1,060
Bex B t	0,980	1,000	1,006	1,020	1,048	1,081

Как видно из таблицы 2, параметр В.,,. = в/ F достаточно близок к теоретическому значению коэффициента биаксиальности B , исключение составляют очень длинные трещины. Поэтому величину Р/ F назовем экспериментальным коэффициентом биаксиальности B_ex . Расхождение между Б_ех и B_t при больших значениях отношения aw , возможно, объясняется, во-первых, применением грубой сетки, а во-вторых, сохранением только двух слагаемых в разложении Вильямса.

Пример 2. Рассмотрим теперь пластину с закреплением участков на боковых сторонах. Размер зон закрепления определим величиной hH (см. Рис.).

Применим комбинированный метод напряжений и перемещений и наряду с Рхх и вод введем коэффициенты биаксиальности вида: Bx = Тхх/(F ст) и Bd = Td/(Fdст), а также их полусумму: Bm = 0,5 (Bx + BD). Эти величины сравним с расчетным параметром B^ . Для определения КИН FD воспользуемся процедурой экстраполяции значений вертикальных перемещений точек на противоположных берегах трещины при приближении к ее вершине [28, 29]. Эти значения отличаются от соответствующих значений КИН, полученных в [32] методом граничных коллокаций, не более чем на 3%.

В таблице 3 представлены результаты расчетов параметра в, КИН, вычисленного с помощью энергетического J-интеграла [27], экспериментального коэффициента биаксиальности B и усредненного коэффициента биаксиальности B в зависимости от размера зон закрепления, а также оценивается погрешность коэффициента биаксиальности, найденного на основании предлагаемых подходов. Видно, что она не превышает 5%.

Таблица 3. Сравнение безразмерных параметров биаксиальности для квадратной пластины при отсутствии смещений на боковой грани в зависимости от размера зон закрепления hH hH = 0,25

aw Параметры 0,2 0,3 0,4 0,5 0,6 0,7 0,8 в -0,686 -0,728 -0,776 -0,809 -0,831 -0,825 -0,787 F 0,963 1,0147 1,107 1,146 1,235 1,311 1,332 Bex -0,712 -0,718 -0,701 -0,706 -0,673 -0,629 -0,591 Bm -0,718 -0,716 -0,701 -0,688 -0,654 -0,607 -0,567 Bex Bm 0,992 1,003 1,000 1,026 1,029 1,036 1,042 hH = 0,5 в -0,726 -0,783 -0,810 -0,843 -0,850 -0,812 -0,705 F 0,961 0,997 1,050 1,099 1,133 1,119 1,022 Bex -0,755 -0,785 -0,771 -0,767 -0,750 -0,726 -0,689 Bm -0,754 -0,784 -0,779 -0,756 -0,741 -0,712 -0,671 Bex Bm 1,001 1,001 1,990 1,014 1,012 1,019 1,027 hH = 0,75 в -0,783 -0,817 -0,845 -0,855 -0,837 -0,766 -0,629 F 0,981 0,995 1,031 1,049 1,029 0,967 0,832 Bex -0,798 -0,821 -0,819 -0,815 -0,813 -0,792 -0,756 Bm -0,800 -0,810 -0,811 -0,799 -0,792 -0,767 -0,728 Bex Bm 0,998 1,013 1,010 1,019 1,027 1,032 1,038 h/H = 1

в	-0,779	-0,792	-0,798	-0,777	-0,728	-0,638	-0,497
F	0,915	0,929	0,924	0,908	0,858	0,779	0,631
Bex	-0,851	-0,852	-0,864	-0,856	-0,848	-0,816	-0,788
Bm	-0,838	-0,837	-0,845	-0,830	-0,819	-0,784	-0,752
Bex B m	1,016	1,018	1,022	1,031	1,036	1,041	1,048

Заметим, что безразмерные параметры, представленные в таблице, могут быть получены на основе лишь экспериментальных данных, причем при нахождении B требуется измерение на всей длине трещины, а при нахождении B — в ряде точек по ее длине. Таким образом, если определить КИН методом экстраполяции вертикальных перемещений, то после одного натурного замера, достаточного для установления параметра в , с помощью только экспериментальных величин можно представить полную характеристику параметров жесткости напряженного состояния у вершины трещины, в частности, по параметру в (при известном значении КИН) оценить значения Т -напряжений.

5.    Заключение

В результате численного моделирования, проведенного в некотором диапазоне изменения геометрических характеристик квадратной пластины с центральной трещиной, установлена связь между параметрами, оказывающими существенное влияние на процесс распространения трещины. Показана возможность приближенной оценки Т- напряжений на основе замера только величины перемещения между вершинами трещины при ее раскрытии. Указанное обстоятельство позволяет ввести понятие экспериментального коэффициента биаксиальности, значения которого (за исключением достаточно длинных трещин) хорошо согласуются с известными теоретическими значениями коэффициента биаксиальности.

Для определения Т- напряжений и коэффициента биаксиальности наряду с численными методами широко используются экспериментальные методы (метод фотоупругих покрытий, сеток, муара, тензометрии, фазовой интерференции, дифракционных решеток и другие). Они дают возможность получить достаточно большой объем информации о распределении перемещений, деформаций и напряжений в образце с трещиной. Сравнение результатов, найденных путем численного моделирования и натурного эксперимента, обеспечивает более достоверный результат при оценке поля напряжений у вершины трещины. Конечно, здесь следует иметь в виду, что реальная геометрия трещины в натурном эксперименте отличается от модели математического разреза, принятого в теории упругости. В то же время предлагаемый в работе подход, основанный на проведении численного эксперимента, может способствовать организации натурных испытаний, в частности, указать места установки датчиков, сформировать параметры, описывающие влияние трещины, а также поможет проанализировать результаты натурного эксперимента.