Численное моделирование течения вязкой жидкости по тепловым измерениям на ее поверхности

Рассматриваются две взаимно связанные между собой задачи. Одна из этих задач условно называется прямой, другая – обратной. Охарактеризуем содержательные стороны этих задач. Прямая задача состоит в определении характеристик потока вязкой жидкости, протекающей в некоторой известной области. Считается, что математическая модель движения жидкости известна, известны также соответствующие исходные (граничные) данные. Искомыми характеристиками в прямой задаче являются поле температур жидкости в известной области, поле скоростей жидкости и переменная вязкость жидкости. Искомыми характеристиками могут быть также распределения вязкости и плотности в известной области или какие-нибудь другие параметры. Обратная задача состоит в определении характеристик потока жидкости по некоторым «избыточным» исходным данным, заданным на части границы известной области. При этом математическая модель движения жидкости считается известной, а на оставшейся части границы области исходные данные заданы с «недостатком» или вовсе не заданы. Один из методов решения обратной задачи состоит в определении «корректных» граничных данных на участке границы с «недостатком» с помощью модели движения и известным граничным данным на участке границы с «избыточными» данными. Затем, с помощью модели движения и всей совокупности граничных данных определяются в результате решения прямой задачи искомые характеристики потока жидкости во всей известной области. Существуют методы, с помощью которых искомые характеристики могут находиться непосредственно по модели движения и граничным данным на участке границы с «избытком». С физической точки зрения «избыточность» граничных данных на некотором участке границы означает доступность этой части границы, возможность делать на ней дополнительные измерения необходимых величин. «Недостаточность» граничных данных на другом участке границы означает недоступность этой части границы, невозможность делать на ней измерения необходимых величин. Для простоты и определенности будут рассматриваться стационарные (установившиеся) варианты задач.

Рассматриваемая обратная задача является, как правило, некорректной и не обладает свойством устойчивости [1, 2], малое возмущение исходных данных на участке границы с переопределением приводит к неконтролируемым ошибкам в определении искомых величин. Обычные классические численные методы не пригодны для решения неустойчивых задач, поэтому для их численного решения требуется применение или разработка специальных методов и алгоритмов. Одна из основных целей данной работы состоит в построении методов и алгоритмов конструктивного устойчивого численного моделирования решения рассматриваемой обратной задачи. Для решения задачи предлагается воспользоваться вариационным методом [1, 2], который основан на сведении исходной задачи к некоторой экстремальной задаче на минимум подходящего целевого функционала (невязки) и минимизации этого функционала каким-либо подходящим методом (например, модифицированными градиентными методами или подходящими квазиньютоновски- ми методами [3-6]). При минимизации целевого функционала организуется итерационный процесс, который фактически сводит исходную задачу к серии устойчивых корректно поставленных прямых задач.

Привлечение моделей механики вязкой жидкости для моделирования различных технологических и природных процессов получило широкое распространение, как в России, так и за рубежом (см., например, [7-12]). В частности, такие модели используются для моделирования различных процессов в земной коре и недрах, в вулканологии, металлургии, стекольном деле и многих других областях [10-12]. Совершенствование измерительных приборов и методов обработки данных позволяет получать более детальную информацию о процессе или явлении. Решение обратных задач восстановления характеристик среды по доступным прямому измерению данным с помощью методов решения некорректных задач является перспективным направлением исследований. Интерес к таким задачам возрастает в связи с увеличением производительности вычислительных мощностей современных ЭВМ и расширяющимся кругом приложений. Совместный анализ данных и результатов численного моделирования приводит к более глубокому пониманию природы явлений. Дополнительные мотивации к теме исследований и анализ состояния вопроса описаны, например, в [10-12].

В данном исследовании разработаны алгоритмы, реализующие вариационный метод для рассматриваемой обратной задачи. Проведены серии вычислительных экспериментов, показавших работоспособность предложенных метода и алгоритмов.

Постановка задачи

Математическая модель установившегося движения вязкой жидкости области Q с R ² с границей Г = Г 1 иГ 2 иГ иГ 4 (рис. 1) в приближении Буссинеска представлена обезразмеренными уравнениями [7, 8]

V-( ^(T) (Vu + VuT )) = Re (u, V) u + V P - RaT e2, xeO,(1)

V • u = 0, x eQ,(2)

V-(X(T) VT) = (u,VT), xeQ,(3)

где x e Q - точка пространства с декартовыми координатами ( x 1 ; x 2 ); u = ( u 1 ( x ); u ₂( x )) - вектор скорости движения жидкости; P = P ( x ) - давление; T = T ( x ) - температура; p = ^ ( T ) - вязкость; X = X ( T ) = k(T ) / ( c p *) - коэффициент температуропроводности; k = k ( T ) - коэффициент теплопроводности; c - удельная теплоемкость; p * - темпе-ратурно независимая плотность; Re - число Рейнольдса [8, с. 87]; Ra - число Рэлея [7, с. 7]; e ₂ = (0; - 1) - единичный вектор; V - градиент; ^T -операция транспонирования; • ,•} - скалярное про

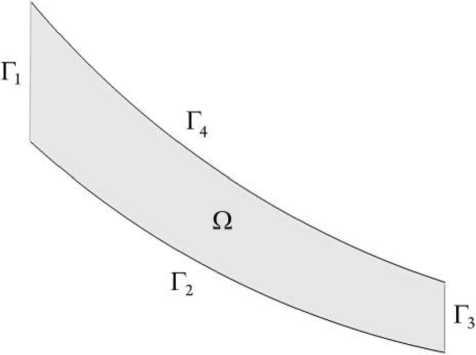
Рис. 1. Область Q и ее граница Г изведение векторов; V * - дивергенция.

Прямая задача состоит в нахождении решения ( T , u , P ) системы уравнений (1)-(3), удовле-

творяющего граничным условиям

Г ! : T = T ] , u = u _T; Г 2 : T = T 2 , u = 0;

Г ₃: T = T ₃, P = 0, a n = 0;                                   (4)

Г ₄ : T = T ₄, (u , n = 0, a n - ( a n , nn = 0;

где a = ^ ( V u + V u ^T ) - тензор вязких напряжений; T 1 , T ₂ , T ₃, T ₄ , u 1 - заданные функции.

Обратная задача состоит в нахождении решения ( T , u , P ) системы уравнений (1)-(3), удовлетворяющего граничным условиям

F , : T = T , , u = u , ; Г ₂ : u = 0;

F ₃: T = T ₃, P = 0 , о n = 0 ;

F ₄ : T = T ₄, k д TI д n = ф , (u , n) = 0, о n - О n , nn = 0 ;

функции T 1 , T ₃, T ₄, ф , u , заданы ( T ₄, ф - результаты измерений температуры и потока тепла).

Метод решения обратной задачи

Дадим вариационную формулировку обратной задаче [9, 10]. Пусть наблюдаемый поток тепла ф на Г ₄ в обратной задаче соответствует некоторому заранее неизвестному распределению температуры T = T ₂ = v * на границе Г ₂ . Пусть T * - компонента решения ( T * , u * , P * ) прямой задачи при условии T = T ₂ = v * на границе Г ₂ в (4), тогда ф = k(T * ) д T * I д n на Г ₄ . Пусть V - некоторое множество допустимых распределений температуры на Г ₂, содержащее в себе элемент v ^* . Для v e V рассмотрим функционал качества

J ( v ) = f( k ( T v ) ( T v - ф )² d F , ∂ n

• ¹    4

где T_v - компонента решения (T_v ,u _v , P_v ) прямой задачи с условием T = T ₂ = v на F ₂ в (4). Функционал качества должен принимать нулевое значение при v = v *, J ( v *) = 0. Искомое граничное температурное распределение v ^* является минимизирующим элементом в вариационной (экстремальной) задаче

J ( v ) ^ min : v e V .

Таким образом, от решения обратной задачи можно перейти к решению вариационной (экстремальной) задачи (5).

Для минимизации целевого функционала часто необходим градиент этого функционала. Градиент находится по правилу

V J ( v ) = k(T ) I z- L , д n ^{1 2}

где z - компонента решения ( z , w , q ) сопряженной задачи

• V-(^(Tv) (Vw + VwT )) = V q + z V Tv + Re (VuJ w -Vwu v), x eQ;

• V- w = 0, x e Q ;

• V- ( A (T_v ) V z ) + {u v , V z ) + Ra (w, e^ = A T v )| [V w + V w ^T , V u _v + V u _V ^T ] + X (T )(V T_v , V z ), x eQ ;

F 1 u F ₂ : z = 0, w = 0;

F ₃: z = 0, q = 0, О n = 0 ( о = n (T_v )( V w + V w ^T ) ) ;

F ₄ : z = 2 1 k (T v ) ^v - ф | , (w , n) = 0, О n - (ст n , n\n = 0.

V     dn    )

Функционал качества минимизируется методом сопряженных градиентов в реализации По-лака-Рибьера [4-6].

Численное моделирование

Для демонстрации работы приведенного алгоритма была разработана программа в пакете инженерных вычислений OpenFOAM ( Open Source Field Operation And Manipulation ). Он представляет собой открытую объектно ориентированную платформу, реализованную на языке программирования С++, обладает большой функциональностью для решения задач механики жидкости и газа, опускает реализацию приложений на мультипроцессорных кластерах. В частности в нем реализованы процедуры решения дифференциальных уравнений с частными производными второго порядка в произвольной пространственной области.

Реализация в пакете OpenFOAM использует широкий набор эффективных процедур аппроксимации дифференциальных операторов, различных типов граничных условий и решения систем линейных алгебраических уравнений, которые возникают после дискретизации краевых задач в пространственных областях с различной геометрией. Программные коды легко адаптировать к изменениям в исходной математической модели и архитектуре вычислителя. Полную информацию о возможностях данного пакета можно найти в [13].

Прямая и сопряженная задачи дискретизировались методом конечных объемов. Тестовый пример рассчитывался на сетке из 1500 гексаэдральных ячеек. Для определения поля скоростей и давления при заданном распределении температуры применялся SIMPLE-алгоритм ( Semi-Implicit Method for Pressure-Linked Equations ) [14]. Для реализации данного алгоритма решались системы линейных алгебраических уравнений (СЛАУ) с положительно определенными и симметричными матрицами с реализацией метода сопряженных градиентов с подходящим предобуславливателем. Для уравнения теплового баланса соответствующие СЛАУ решалась бинаправленным методом сопряженных градиентов [15]. Для аппроксимации оператора Лапласа всюду выбиралась линейная схема Гаусса с коррекцией потока, для аппроксимации конвективного оператора – TVD схема с ограничителем minmod [16]. Для расчетов использовалось одно ядро CPU Intel Core i5, 2,6 GHz, RAM 16 MB, OS X 10.10. Одна итерация метода сопряженных градиентов рассчитывалась примерно 15 мин. (решение прямой и сопряженной задач и определение шага спуска в методе сопряженных градиентов).

Уточним модельную область Ω . Граница области состоит из следующих частей: Γ1 есть от- резок прямой линии, соединяющий точки (0; 2,5) и (0; 1,5); Γ2 – дуга окружности, соединяющая точки (0; 1,5), (1,5; 0,5) и (3, 0;0); Γ3 – есть отрезок прямой линии, соединяющий точки (3,0; 0) и (3,0; 0,5); Γ4 – дуга окружности, соединяющая точки (3,0; 0,5), (1,5; 1,2) и (0; 2,5).

Фиксируем следующие характерные значения параметров в модели, соответствующие усредненным значениям в потоке лавы [11, 12, 17]: α = 10^–5 K^–1, g = 9,8 м/с², h = 10 м, ρ _ref = 3000

кг/м³, µ _ref = 3,5·10⁹ Па с, T_ref = 300 K, T _* = 1473 K, T_c = 1273 K, ∆ T = T _* - T_ref , λ _ref c_ref = 1200 J/кг K, u_ref = 10^–3 м/c, откуда получаем значения Ra = 100, Rе = 8,5·10^–8.

=10–6 м2/c,

В модельных расчетах принимается зависимость вязкости от температуры µ ( T ) = 1 + ¹ ₂10³ ( 1 + tanh( - 100( T ref T - T c )) ) .

Принимается зависимость коэффициента теплопроводности от температуры [16]

k (T ) = ^

1,15 + 5,9 - 10 ^{- 7}( T ref T - T * ) 2 U5 + 9,7 - 10 ^{- 6}( T ref T - T * )²,

T_ref T <  T _* , T ref T ^> T * .

На границе Γ ₁ задается температура T ₁( x ₁, x ₂) = 5,0 - 0,5( x ₂ - x ₂ ^B ) , x ₂ ∈ [ x ₂ ^B , x ₂ ^A ] , и u ₁( x ₂) = U ( x ₂) n ₁ , где n ₁ = ( 2 2; - 2 2) и U ( x ₂) есть парабола, проходящая через три точки: U ( x ₂ ^A ) = 10,    U ( x ₂ ^B ) = 0,    U (0,5( x ₂ ^A + x ₂ ^B )) = 7,25 .

скорость

Температура            T3(x1,x2) = 3,5 - 2(x2 - x2D) , x2 ∈ [x2D,x2E], на Γ3 и T4(x1,x2) = 4,5 -2(x1 - x1A)/3, x1 ∈[x1A ,x1E ] , на Γ4 .

Интерес представляет область повышенной вязкости, так как она «тормозит» течения и тепловой поток. Увеличение вязкости жидкости опреде

ляется по пороговым значениям вязкости как под-    Рис. 2. Область повышенной вязкости (черная)

множество G ⊂ Ω , в точках x ∈ G которого µ ( T ( x )) ≥ µ_ε , где µ_ε = µ _max - ε ( µ _max - µ _min), 0 ≤ ε ≤ 1.

Короткий А.И., Численное моделирование течения вязкой жидкости Цепелев И.А. по тепловым измерениям на ее поверхности

На рис. 2 показано местоположение области повышенной вязкости, которую необходимо восстановить. На рис. 3 иллюстрируетcя точность восстановления области повышенной вязкости на шагах итерации n = 0, 5, 10, 30 при ε = 0,5 .

Рис 3. Точность восстановления области повышенной вязкости

Рис. 4. Распределение температуры в расчетной области

На рис. 4 показано распределение температуры в области Ω ; на рис. 5 – точность восстановления температуры T ^{( n )} ( x ) - T ^*( x ) на шагах итерации n = 0, 5, 10, 30.

На рис. 6 показано поле распределения скоростей в области Ω ; на рис. 7 – точность восстановления поля скоростей || u ( n ) (x) - u (x) || на шагах итерации n = 0 и n = 30.

Результаты расчетов показывают, что последовательность приближений метода сопряженных градиентов минимизирует функционал невязки устойчивым образом. Для данной аппроксимации расчетной области относительные точности решения систем линейных алгебраических уравнений в SIMPLE методе и методе решения уравнения теплового баланса составляли 10–2, что согласуется с точностью аппроксимации дифференциальных операторов на заданной неструктурированной сетке. Для тестового примера приемлемый уровень точности решения обратной задачи в определении температуры и поля скоростей достигается примерно за 30 итераций.

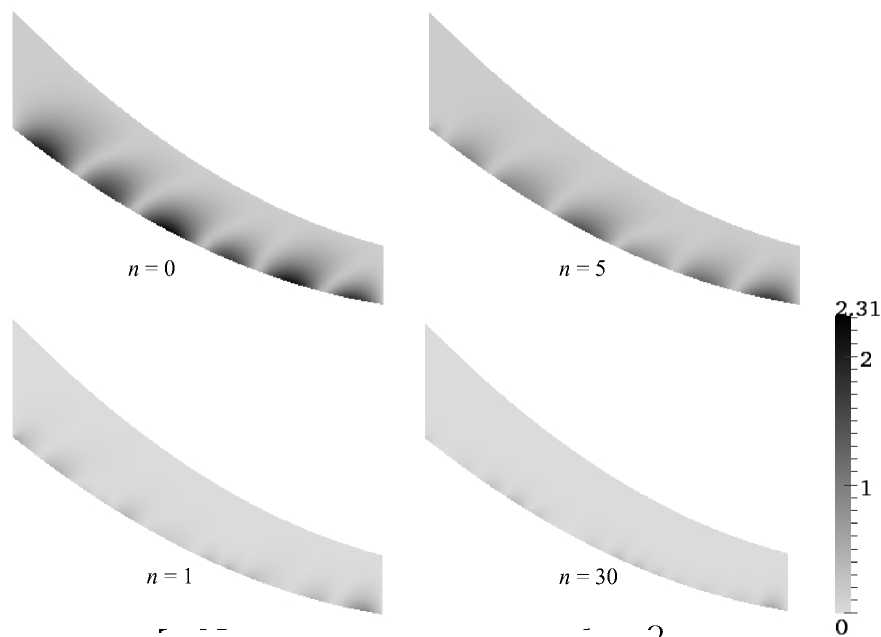
Рис. 5. Точность восстановления температуры в области Ω

Рис. 6. Поле скоростей в расчетной области

Заключение

Разработан алгоритм численного решения неустойчивой обратной граничной задачи механики вязкой жидкости, устойчивый к вычислительным погрешностям. Данный алгоритм основан на сочетании аналитических методов исследования математической модели и эффективных устойчивых методов решения экстремальных задач. Реализация алгоритма в пакете OpenFOAM позволила создать программные коды для решения рассматриваемой задачи, соответствующие современному уровню развития вычислительной техники и программного обеспечения для этой техники.

Работа выполнена при поддержке РФФИ (проект № 14-01-00155) и Комплексной программы фундаментальных научных исследований УрО РАН (проект 15-16-1-10).