Численное моделирование течения жидкости в венозном клапане при пробе Вальсальвы

Уильям Гарвей почти 400 лет назад доказал, что здоровый (состоятельный) венозный клапан играет ключевую роль в односторонней циркуляции крови. Данное наблюдение лежит в основе современного понимания кровообращения. Однако мало что известно о механизме работы венозных клапанов. Функция вен состоит в беспрепятственном проведении крови по направлению к сердцу и недопущении обратного ее тока [21]. Данная функция обеспечивается клапанами в просвете вены и нарушается, если створки клапана закрываются не полностью или слишком медленно, пропуская значительный объем крови в обратном направлении. В последнее время для диагностики этих нарушений применяется ультразвуковое доплеровское исследование для оценки величины и направления скорости кровотока, однако возможности такой диагностики ограничены. Створки настолько тонкие, что их не удается визуализировать, и единственный параметр, используемый врачами сегодня для оценки функции клапана, – это длительность обратного тока крови. Ее измерение проводится во время нагрузочных функциональных тестов, создающих импульс обратного перепада давления. Самый простой из них, так называемая проба Вальсальвы, или проба с натуживанием, состоит в кратковременном повышении давления на выхо-

5202-6398

Эта статья доступна в соответствии с условиями лицензии Creative Commons Attribution-NonCommercial 4.0 International

License (CC BY-NC 4.0)

This work is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License (CC BY-NC 4.0)

де из клапана, которое вызывает его закрытие на период проведения пробы [11; 17; 27]. Для здорового венозного клапана проба приводит к полной остановке венозного кровотока после кратковременного обратного тока крови (менее 1 c), а для больного – обратный ток крови наблюдается более 1 с. Отсутствие возможности визуализировать движение неизмененных створок клапана и отсутствие достоверной информации о значении других характеристик кровотока, таких как объемная и пиковая скорость, создают предпосылки для математического моделирования недостающих звеньев в понимании этого фундаментального биологического процесса.

Математическое моделирование кровотока при пробе Вальсальвы выполняется в основном с помощью модели сосредоточенных параметров. Такой подход заключается в создании, подобно электрической схеме, разветвленной сети кровеносных сосудов – артерий и вен, и получении на ее основе информации о базовых характеристиках – расходах и давлениях – на каждом участке этой сети [12; 15; 19; 22; 23; 26]. Авторами этих работ смоделирована реакция отдельных частей кровеносной системы на пробу Вальсальвы при нормальных и патологических условиях, таких как, например, сердечная недостаточность, дыхательная синусовая аритмия и т.д. Однако полезная врачам локальная информация о течении – расположении и размерах застойных областей, областей турбулизации, зонах с критическими значениями давлений и сдвиговых напряжений, может быть получена только из двумерного или трехмерного численного моделирования. Существует большое количество таких публикаций для венозных клапанов в тех или иных физиологических состояниях в зависимости от упругости створок клапана, от действия окружающих вену мышц и т.д. [2; 3; 6; 8; 9; 20; 29; 28; 31]. Ранее авторами статьи были разработаны модели здорового и несостоятельного клапана подколенной вены, исследовано влияние упругости створок на поле скорости и застойную область за створками клапана [14; 30]. На основе данной модели было рассчитано течение в клапане после хирургической операции экстравазальной коррекции [13]. Результаты расчетов показали хорошее согласие с клиническими данными по амплитуде колебаний створок, положению и размерам застойной области. Работ, в которых проведено численное моделирование течения в венозном клапане при пробе Вальсальвы, авторами не обнаружено.

Цель работы – исследовать влияние упругости створок на поле скорости, продолжительность и объем обратного кровотока при пробе Вальсальвы с помощью численного моделирования течения в клапане подколенной вены.

Материалы и методы

Объектом исследования в данной работе является клапан подколенной вены человека [10; 18; 24]. Подколенная вена относится к глубоким венам. Она располо- жена между бедренной веной и венами голени. Ее длина составляет около 8 см. Известно, что в подколенной вене встречается 2–3 клапана, два из которых расположены в ее истоке и устье. Чаще всего венозные клапаны являются двустворчатыми. Доля одно- и трехстворчатых клапанов составляет менее 20 %. В работе рассматривается клапан, расположенный примерно посередине подколенной вены, и поэтому условия разветвления потока оказывают минимальное влияние на кровоток в нем. Интерес врачей к подколенной вене связан с опасностью тромбозов, которые чаще всего поражают глубокие вены нижних конечностей.

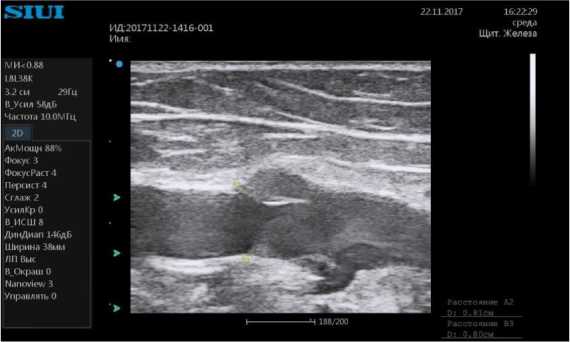
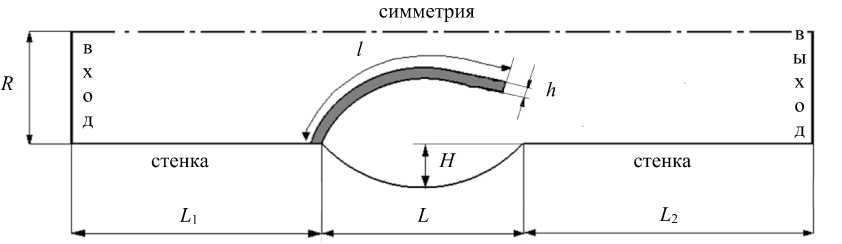
Модель клапана подколенной вены построена на основе собственных клинических измерений в плоскости симметрии клапана (рис. 1, а ). Геометрическая модель клапана характеризуется радиусом вены R , длиной l и толщиной створки h , длиной L и глубиной H синуса (расширения за клапаном). Длины областей перед клапаном L 1 и за клапаном L 2 – взяты достаточными для того, чтобы не оказывать существенного влияния на течение в клапане. Численные значения указанных параметров приведены в табл. 1. Построенная модель является симметричной. Данное допущение оправдано тем, что поток в клапане близок к плоскому, благодаря вытянутой форме створок в нормальном к центральной плоскости направлении. Кроме того, введенное допущение симметрии течения относительно оси вены исходит из того, что клапан является двустворчатым.

Таблица 1

Геометрические параметры модели клапана подколенной вены

R , мм	L 1 , мм	L 2 , мм	L , мм	H , мм	h , мм	l , мм
5	25	36	9	2	0,5	10

Проведен сопряженный расчет течения жидкости и движения упругой створки с помощью технологии fluidstructure interaction (FSI) в обобщенной лагранже-эйлеровской постановке. Гидродинамические расчеты выполнялись в Ansys Fluent , механические – в Ansys Mechanical . Связка двух систем происходила в System Coupling в среде Ansys Workbench .

Течение жидкости моделируется с помощью уравнений движения вязкой несжимаемой жидкости (уравнений Навье – Стокса) (1)–(2):

μ

— + ((V - V m ) -V ) V =-- V p + f- V V ² V .    (1)

5 t                      p f      p f

V- V = 0,                    (2)

б

Рис. 1. Изображение клапана подколенной вены в B -режиме ( а ) и расчетная область (половина геометрической модели симметричного венозного клапана) ( б )

где V - скорость жидкости в узлах динамической сетки,

Vm - скорость узлов расчетной сетки в точке, рf и цf -плотность и вязкость жидкости; рf =  1060 кг/м3, цf = 0,004 Па^с [1]. Характерное число Рейнольдса, построенное по диаметру вены и скорости течения в состоянии покоя, равно 132.

Движение створки моделируется с помощью уравнений эластодинамики для линейного однородного изотропного материала (3):

d2 d

Р = v 2 + Р fb,              (3)

где d - перемещение створки, f _ъ- массовая сила со стороны жидкости, § = ^( V d + ( v d ) ) - тензор деформаций, 2 - тензор напряжений, 2 = 2ц§ + 1 X tr (§) -уравнение состояния, X, ц - коэффициенты Ламэ. Эти параметры удовлетворяют следующим соотношениям (4):

.      E v           E

X =-------------- , ц =------- ,

(1 + v)(1 - 2v)     2(1 + v)

где E - модуль Юнга, v - коэффициент Пуассона. Механические свойства створки клапана взяты из расчет- ных работ, использующих двумерные модели клапанов [7; 29]: E = 0,2-20 МПа, v = 0,45, р = 1200 кг/м3. При разработке математических моделей в указанных исследованиях значения модуля Юнга подбирались с целью обеспечения открытия створки клапана в физиологическом диапазоне. Отметим, что измеренный модуль Юнга для здорового бычьего венозного клапана имеет значение около 10 МПа при радиальном растяжении [4].

На входной границе для расчета течения в модели здорового венозного клапана в состоянии покоя задавалась постоянная во времени среднерасходная скорость V_{b 0} = 0,05 м/с [30] с плоским профилем, в расчетах с пробой Вальсальвы - импульсное изменение давления во времени A p ( t ) (рис. 4), на выходе - нулевое противодавление. На верхней границе задано условие симметрии, на нижней - условие прилипания. Стенка вены моделировалась абсолютно жесткой ввиду малости ее перемещений. На поверхности створки задавалось условие сопряжения между твердой и жидкой областями (5):

ГГ  ГГ  Г  Г ds = df, Vs = Vf,  Fs = Ff,           (5)

где d - перемещение, V - скорость, F - усилие.

а

б

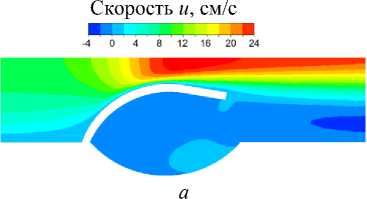
Рис. 2. Расчетные гидродинамическая и механическая сетки в фазы открытого ( а ) и закрытого ( б ) клапана

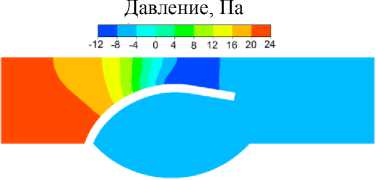
Рис. 3. Поля продольной скорости ( а ) и давления ( б ) в модели здорового венозного клапана в состоянии покоя ( E = 0,2 МПа)

На рис. 2 показаны расчетные гидродинамическая и механическая сетки в два момента времени. Сетки построены в программе Ansys Meshing. Проведены исследования на чувствительность результатов расчета к размеру сеток и шага по времени. Гидродинамическая сетка состояла из 64 558 треугольных элементов и имела сгущение к створке клапана и стенке вены. Механическая сетка состояла из 500 прямоугольных элементов. Для настройки гидродинамической сетки использовались алгоритмы Smoothing и Remeshing, которые осуществляют сглаживание и перестроение сетки и устраняют в процессе расчета появление вырожденных ячеек сетки, приводящих к остановке расчета. Решалась контактная задача о соударении створок венозного клапана, при этом вторая створка заменялась при моделировании контакта прямой пластинкой и располагалась вдоль оси вены. Шаг по времени составлял 0,01 с, на этапе решения контактной задачи временной шаг уменьшался до 0,001 с.

Результаты

Известно, что в состоянии покоя створки здорового клапана не смыкаются, полуширина проходного сечения составляет около 30 % от радиуса, а течение ввиду малых частоты и амплитуды колебаний створок практически не отличается от течения с постоянным расходом [21]. На входной границе модели задавалась постоянная во времени среднерасходная скорость Vb0 = 0,05 м/с [30]. Для получения в модели положения створки в состоянии покоя, соответствующего физиоло- гическому диапазону, расчеты проводились для разных значений модуля Юнга E створки в диапазоне 0,2–20 МПа. Расчеты начинались от заданного начального поля скорости в виде покоящейся жидкости и начального положения створки в закрытом состоянии и длились, пока клапан не откроется и характеристики течения, и положение створки не перестанут меняться во времени.

В результате расчетов было установлено, что при значении модуля Юнга E = 0,2 МПа открытие клапана соответствует физиологическому – расстояние от створки до оси составляет 30 % радиуса [21], продолжительность перехода на установившееся течение T 1 = 1 c, а перепад давления на клапане ∆ p 1 = 22 Па. На рис. 3 показаны рассчитанные для состояния покоя клапана поля продольной скорости ( а ) и давления ( б ).

Выполнены расчеты течения в модели здорового венозного клапана для граничных условий, соответствующих пробе Вальсальвы. Данные граничные условия реализуются при импульсном изменении давления на входной границе, которое состоит из трех временных участков (рис. 4). Первый – длительностью T 1 и с постоянным положительным перепадом давления ∆ p 1 – соответствует течению в состоянии покоя клапана. Указанные характеристики были получены из предыдущего расчета течения в здоровом венозном клапане в состоянии покоя. Второй участок – длительностью T 2 и с постоянным отрицательным перепадом давления ∆ p 2 – соответствует условиям пробы Вальсальвы. В начале и в конце этого участка давление линейно меняется между постоянными уровнями ∆ p 2 и ∆ p 1 в течение короткого промежутка времени τ. Третий участок – длительностью T 3 и с постоянным положительным перепадом

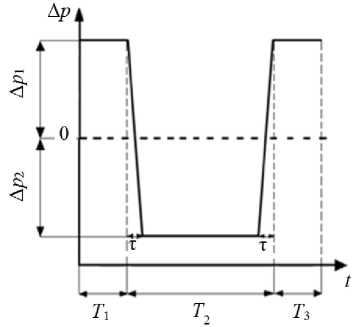
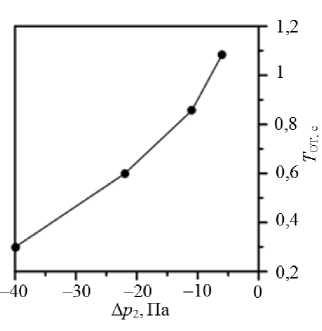
Рис. 4. Давление на входной границе участка вены Рис. 5. Зависимость длительности обратного течения с клапаном (импульсный перепад давления), моде-        от величины обратного перепада давления лирующее пробу Вальсальвы

Скорость u , см/с                                ^{Скорость u , см/с}

.^™                1                                                    -24 -21 -13 -15 -12 -9-6-3 0 3

а                                                б

Рис. 6. Поля продольной скорости для клапанов с модулем Юнга E = 0,2 МПа ( а ) и 20 МПа ( б ) в момент времени, соответствующий середине длительности пробы Вальсальвы

давления ∆ p 1 – соответствует возвращению течения к состоянию покоя. Известно, что длительность обратного течения при пробе Вальсальвы в здоровом венозном клапане составляет менее 1 с [11]. Перепад давления ∆p 2 варьировался в диапазоне от –5 до –40 Па с целью получения длительности обратного течения, близкой к соответствующему значению для здорового венозного клапана (0,5 с) [11]. Результаты расчета показаны на рис. 5.

Получено, что для значения ∆ p 2 = –22 Па длительность обратного течения составила 0,6 с, что близко к физиологическому значению, поэтому данное значение ∆ p 2 было выбрано для исследования влияния упругости створок на течение в клапане при пробе Вальсальвы. Численные значения рассчитанных параметров пробы Вальсальвы приведены в табл. 2.

Таблица 2

Параметры импульсного изменения давления на входной границе участка вены с клапаном (проба Вальсальвы)

T 1 , c	T 2 , c	T 3 , c	τ, c	∆ p 1 , Па	∆ p 2 , Па
1	3	1	0,3	22	–22

Для импульсного изменения давления с параметрами пробы Вальсальвы (табл. 2) выполнено исследование влияния модуля Юнга створки клапана в диапазоне от 0,2

до 20 МПа на продолжительность обратного течения T от , время закрытия клапана T закр и относительный объем утечек через клапан V от (отношение объема утечек к объему прямого тока в состоянии покоя за время пробы Вальсальвы), который рассчитывался следующим образом:

V т = J V b dt / ( V b 0 Т ) , (6)

( Т_г)

где V b – среднерасходная скорость течения, V b 0 – среднерасходная скорость течения в состоянии покоя, T 2 – длительность пробы Вальсальвы.

Нужно отметить, что относительный объем утечек может быть рассчитан по результатам ультразвуковых измерений и использоваться как дополнительный параметр наряду с продолжительностью обратного тока для диагностики венозных клапанов.

На рис. 6 показаны распределения продольной скорости для клапанов с разными модулями Юнга в момент времени, соответствующий середине длительности пробы Вальсальвы (2,5 с). В клапане с E = 0,2 МПа створки закрыты, а с E = 20 МПа створки открыты, и скорость обратного тока между створками равна 24 см/с.

На рис. 7, слева, изображены расчетные изменения среднерасходной скорости во времени для клапанов с разными модулями Юнга. В течение первой секунды прямой поток через рассмотренные модели клапана нарастает, достигая установившегося состояния. В мо- а

б

в

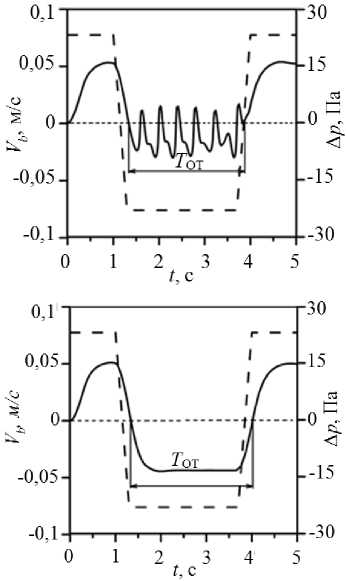
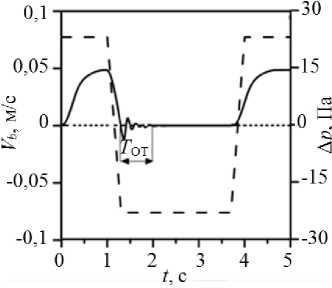
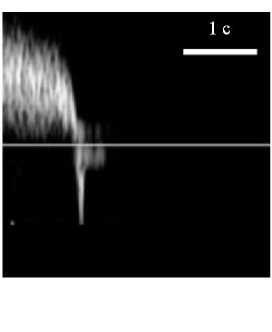
Рис. 7. Изменения среднерасходной скорости (сплошная линия) для здорового клапана (0,2 МПа) ( а ), несостоятельных клапанов 2 МПа ( б ) и 20 МПа ( в ) при воздействии обратного перепада давления (пунктирная линия) при пробе Вальсальвы (результаты собственных расчетов и ультразвуковые доплеровские измерения скорости кровотока [5; 16; 25])

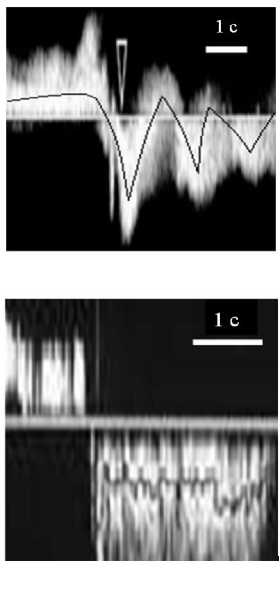
мент времени начала пробы Вальсальвы (t = 1 c) клапаны открыты. Для клапана с E = 0,2 МПа наблюдаем, что длительность обратного течения Tот = 0,6 с, что соответствует доплерограмме здорового клапана (рис. 7, а, справа) [25]. Напротив, для клапана с E = 20 МПа наблюдаем, что длительность обратного течения Tот = 2,7 с равняется времени действия обратного перепада давления при пробе Вальсальвы, что соответствует до-пплерограмме для несостоятельного клапана (рис. 7, в, справа) [16]. Промежуточный случай модели клапана, с упругостью створки 2 МПа, реализует достаточно интересную реакцию клапана на пробу Вальсальвы, при которой створки в течение всей пробы полностью не смыкаются, а совершают колебательное, медленно затухающее движение, то открывая, то закрывая клапан (рис. 7, б, слева). Этот вариант также находит свое подтвер ждение в клинических наблюдениях (рис. 7, б, справа) [5]. На рис. 8 показаны рассчитанные значения продолжительности обратного течения и относительного объема утечек. Для случаев 0,2 и 20 МПа продолжительность обратного течения и объем утечек приводят к качественно одинаковым результатам - малые Тот (<1 с) и большие значения Vот (> 0,5) соответственно. Однако в случае с E = 2 МПа картина противоположная: продолжительность обратного течения большая (Тот = 2,5 с), а объем утечек - малый (Vот = 0,19). Данный результат можно объяснить тем, что продолжительность обратного течения рассчитывается от начала и до завершения обратного течения, без учета внутренних промежутков прямого течения, в то время как объем утечек, будучи интегральной величиной, учитывает разницу объема прямого и обратного тока за это время.

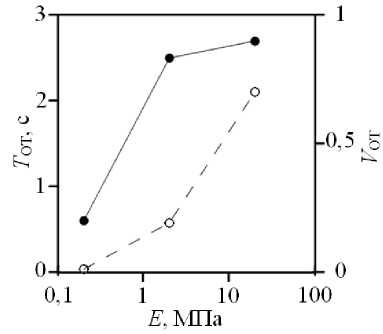
Рис. 8. Продолжительность обратного течения (черные точки) и относительный объем утечек (белые точки) для клапанов с разными модулями Юнга

Клапан полностью закрывался из рассмотренных случаев только при E = 0,2 МПа, время закрытия клапана Tзакр, полученное из анализа перемещения створки, составило 0,4 с – это в 1,5 раза меньше, чем продолжительность обратного течения. Данный результат объясняется тем, что после смыкания створки клапана выгибаются, увеличивая площадь соприкосновения (коапта- ция створок) и еще некоторое время проталкивая жидкость в направлении обратного течения.

Заключение

Впервые разработана вычислительная модель для исследования течения в венозном клапане подколенной вены при пробе Вальсальвы. Разработанная модель течения протестирована по длительности обратных токов с использованием результатов ультразвуковых доплеровских измерений скорости кровотока для здорового и несостоятельного клапана. Для модели здорового клапана длительность обратного тока была меньше 1 с, а для несостоятельного клапана – больше 1 с, что соответствует клиническим результатам. Для модели несостоятельных клапанов обнаружено два режима движения створок при проведении пробы Вальсальвы – постоянно открытое состояние и колебания с периодическим закрытием-открытием. В перспективе разработка трехмерной модели венозного клапана позволит уточнить обнаруженные эффекты и закономерности.

Vol. 35, no. 2. – P. 1–21.

Финансирование. Работа выполнена при финансовой поддержке Минобрнауки России в рамках госзадания «Изучение регуляторных механизмов сердечно-сосудистой, нервной и дыхательной систем для разработки новых подходов к выявлению ортостатических расстройств и вегетативной дисрегуляции при колебательных постуральных нагрузках» (№ 122020300239–8).

Результаты получены при использовании ресурсов СКЦ «Политехнический» СПБПУ.