Численное моделирование технологических напряжений при изготовлении пластмассовой изоляции провода

R.R. Zinnatullin and N.M. Trufanova

Perm State Technical University, Perm, 614990, Russia

Numerical modeling of different cooling modes of a wire with polymeric insulation has been carried out. The process of cooling of the wire is accompanied by heat exchange between the polymer insulation, the environment and the conductor, formation of the polymer crystalline structure and considerable thermal emission induced by phase transition, and occurrence of technological stresses in the insulation. Temperature-conversional fields and technological stresses in the polymer have been obtained and studied. A criterion for forecasting cavern formation has been determined. The air-to-water cooling modes are offered, which makes it possible to avoid the occurrence of radial stretched stresses in insulation critical zones and to increase the insulation rate.

Производство проводов с изоляцией из полиэтилена низкого давления (ПЭНД) осуществляется на экструзионной линии. Одним из условий, обеспечивающих качество получаемой изоляции, является рациональный процесс её охлаждения.

Для реализации различных режимов охлаждения (воздушного, водяного, воздушноводяного, воздушно-капельного и комбинированного) используется охлаждающая ванна, схематическое изображение которой представлено на рисунке 1 [1]. Водяное охлаждение без воздушных промежутков между ваннами с водой получается путем сближения соседних перегородок 3 устройствами 7 . Чередованием водяных и воздушных промежутков осуществляется воздушно-водяное охлаждение. При воздушно-капельном охлаждении вода из ванн отводится через сливы 4 , а изолированный провод опрыскивается водой через устройство 8 . При комбинированном охлаждении используются различные сочетания первых трех режимов.

Охлаждение провода происходит в условиях неоднородного температурного поля и фазовых превращений в изоляции, что приводит к неоднородным полям деформации и напряжений полимера. В результате, при определенных технологических условиях, появляются пустоты (каверны) в изоляции и отслоение полимера от токопроводящей жилы, что не может быть допустимо с точки зрения качества изделия.

@ Р.Р. Зиннатуллин, Н.М. Труфанова, 2009

r

Рис. 1. Схема ванны охлаждения изолированной жилы: 1 — секция с водой; 2 — воздушный промежуток;

3 — перегородки с эластичным уплотнением; 4 — слив воды; 5 — изолированный провод;

6 — подача воды; 7 — механизмы для передвижения перегородок; 8 — трубы с форсунками

Для определения причин нарушения сплошности изоляции и потери контакта с жилой поставлена и численно решена задача определения напряженно-деформированного состояния изолированной жилы при различных условиях охлаждения.

Исследуемый провод представляет собой осесимметричную конструкцию из двух разнородных материалов: медь или алюминий (жила) и ПЭНД (изоляция) (Рис. 2). Задача решается в два этапа: на первом этапе рассматривается температурная задача, на втором — механическая, с использованием результатов решения температурной задачи.

Процесс охлаждения полимера является экзотермическим. В работе принимаются допущения: 1) характер процесса стационарный; 2) изолированная жила обладает осевой симметрией геометрии, свойств, условий охлаждения и движется с постоянной скоростью; 3) материалы жилы и изоляции изотропны; 4) изменения размеров провода, вызванные усадкой изоляции, не учитываются.

Распределение температуры T ( r, z ) в металлической жиле удовлетворяет уравнению теплопроводности:

5 T 1 Г 1 д ( T ) d 5 T )

r e ( 0, R ж ) ,     z e ( 0, L ) .                    (1)

V — =---I r X — 1+—I X— I

5 z c p L r d r V   5 r ) 5 z V 5 z )

где r и z — радиальная и осевая координаты; L — длина участка охлаждения; V — компонента скорости в направлении оси провода; T — температура; p — плотность; c — удельная теплоемкость; X — коэффициент теплопроводности.

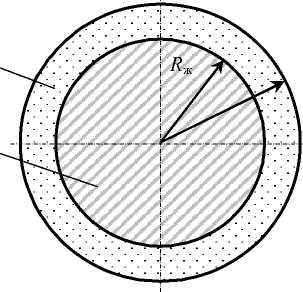
R из

Рис. 2. Сечение провода: 1 — металлическая токопроводящая жила; 2 — изоляция из ПЭНД; R ж — радиус жилы; R и з — радиус изолированного провода

Охлаждение изоляции сопровождается кристаллизацией полимерного материала. Для количественной характеристики степени завершенности фазового превращения используется параметр β, принимающий значения от 0 до 1 и называемый относительной степенью кристалличности [2].

Определение полей температур T ( r, z ) и степени кристалличности β( r, z ) в изоляции заключается в совместном решении уравнения теплопроводности и кинетического уравнения [2]:

V   =1_ дz c р

др д z

V

1 д ( , дТА д L дТА --1 r X— 1 +—I X— I r д r V д r ) д z V д z )

K ₀ exp

U     У Т пл )

RT Т(Т пл - T ) ^J

+ Q v , r g ( R ж , R из ) , z g ( 0, L ) ,

( 1 + C 0 P ) [P p ( T H]

r g ( R ж , R з ) , z e ( 0, L ) , (3)

vQ m дв

Qv         ~ , c дz где Tпл = 415 К — равновесная температура плавления ПЭНД; R — универсальная газовая постоянная; Q v — скорость удельного тепловыделения при кристаллизации; Qm = 377 кДж/кг — экспериментально определенное максимальное тепловыделение при кристаллизации ПЭНД; Pp — равновесная относительная степень кристалличности ПЭНД (максимально возможная относительная степень кристалличности при определенной температуре); C0 = 1,8, K0 = 0,04 с-1, U = -1000 Дж/моль, у = 316 К — экспериментально полученные параметры кинетического уравнения (3). Основой для их определения служат результаты эксперимента [3], описывающие изменение удельного тепловыделения в образце из полиэтилена в условиях охлаждения с постоянной скоростью.

Краевые условия для системы (1)–(2) имеют вид:

T z . 0 = Т ж , r ® [ 0. R ж ) ,   Т| ₌ = 0 = Т из ,   в z = 0 = 0,   r 6 [ R ж , R „] ,                       (5)

= 0, r е [ R ж , R ,„] ,                                                                 (6)

д Т д r

= 0, r = 0

z е ( 0, L ) ,

X

д Т

= Т\

I r = й ж + 0 ,

z g ( 0, L ) ,

ж дr r=«ж -0

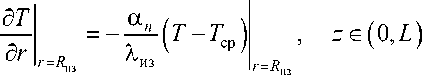
где a n — коэффициент теплоотдачи на поверхности провода; T_cp — температура охлаждающей среды; Т_ж и Т из — начальная температура жилы и изоляции, соответственно.

Для определения a n используется эмпирическая зависимость для случая продольного обтекания цилиндра [4], учитывающая связь входящих параметров и температуры [5].

Задача о напряженно-деформированном состоянии охлаждаемого провода формулируется в рамках следующих допущений: 1) не учитываются силы инерции; 2) используется гипотеза о плоско-деформированном состоянии (в _z =0); 3) провод является осесимметричным; 4) принимается условие малости деформаций.

Термомеханическое поведение кристаллизующегося полимера рассматривается в рамках модели, предложенной в работе [6], в соответствии с которой определяющие соотношения для материала изоляции имеют следующий вид:

стr (r,z) = (1 -Р(r,z))х f 2                                                                                        .ll

^X - I Ba ^- 3 M a I [⁰ ( r , ^Z ) ^{- 3 a} a ^{( T (} r , ^Z ) ^{- Т} из ) ] + ² M a [^S r ( r , ^Z ) ^{- a} a ^{( T (} r , ^Z ) ^{- Т} из ) ]+

P ( r ^, z ) 17        2 ^

+ J - I B k - ₃ m k l[⁰ ( r , z ) ^-0 ( r , ^z ) ^{- 3 a} k ⁽ T ⁽ r , ^z ) ^- T ⁽ r , ^{Z ))} ]

+

+ 2Mk [Sr (r, Z) - Sr (r, Z) - ak (T(r, Z) - T(r, Z))] + BkЮ * dP(r,Z) , r C( Rж, Rиз ) , Z C( 0, L ) , стф(r, z ) = (1 -P(r, z ))X

X-f B a -1M a JlX r , z ) - 3 a a (T ( r , Z ) - T „ ) ] + 2 _Ц a [= , ( r , z ) "« a (T ( r , Z ) - T„ ) ]l +

P( ^r > ^z ) u             A

+

r ’ z )                   2

J 11 B k -TM k |[⁰ ( r , ^Z ) ^-0 ( r , ^Z ) ^{- 3 a} k ^{( T (} r , ^Z ) ^{- T (} r , ^{Z ))} ]

A I 3 Л

+

+ 2Mk [£Ф (r,z)- £Ф (r,z)- ak(T(r,z)- T(r,Z))] + Bkю  ’de (r,z), r e( Rж, Rиз ) , Z e( 0, L ) , где 0 = гr + £ф, а sr и £ф — радиальные и окружные деформации; стr и стф — радиальные и окружные напряжения; ю = 0,1 — коэффициент объемной усадки ПЭНД вследствие кристаллизации; a a , a k — коэффициенты линейного расширения аморфного и полностью закристаллизованного полимера соответственно; Ba, Bk и мa, мk — соответственно объемный и сдвиговой модули для аморфного и закристаллизованного полимера; z — осевая координата.

Для металлической жилы физические соотношения принимаются в виде закона Гука для изотропной среды с учетом температурных деформаций [7]. Все значения коэффициентов и переменных величин для полимера в расплавленном состоянии соответствуют температуре 300°С ( a a = 2,044 - 10 ^{- 4} К^-1; B a = 3,33 - 10⁷ Па;

ц a = 3,34 - 10⁵ Па), в кристаллическом состоянии — температуре 0°С ( a k = 3,542 - 10 ⁵ К 1 ; B k = 1,78 - 10⁹Па; ц k = 5,93 - 10⁸Па) [9].

Таким образом, краевая задача о напряженно-деформированном состоянии в изолированном проводе включает соотношения (10)-(11) и следующие уравнения:

о r = ( B - ² ц )( 0 - 3 a (T - Т ж )) + 2 ц ( в _r - a ( Т - Т _ж)),

₂                                                     г е [ ^0, R _ж ] , z е ( 0, L )      (12)

о , = ( B - у ц )( 0 - 3 a (T - Т ж )) + 2 ц ( е _ф - a ( Т - Т ж )),

'Т’.° °    0, г€(0,Rиз), zе(0,L), дг      г ег = ^U,  еф= U, г е (0, R из),    z е(0, L), дг     г г

^Ul = 0 = ⁰,    ^Ul = R ж - 0 = U t = R ж + 0 ,

° г

¹ г = R ж - 0

= ° г

' г = R ж + 0 ,

° г

^г = R из

= 0,

где U — радиальное перемещение.

Конечномерные аналоги температурно-конверсионной (1)-(9) и термомеханической (10)-(17) задач построены по методу конечных разностей. Выбраны следующие конечно-разностные сетки:

® 1 = { z j = h z ( j - 1 ) • j = 1,2,..., N z ;    h z = L /( N z - 1) } ,

' \ = { г . = h . ( i m - 1 ) , i m = 1,2,..., N . ) h m = R ж /( N m - 1) } ,                       (18)

® 3 = { г , = R ж + h p ( i p - 1 ) , i p = 1,2,..., N p ; h p = ( R „ - R ж )/( N р - 1) } ,

№ = № 1 х ( ю ₂ +Ю ₃ ) .

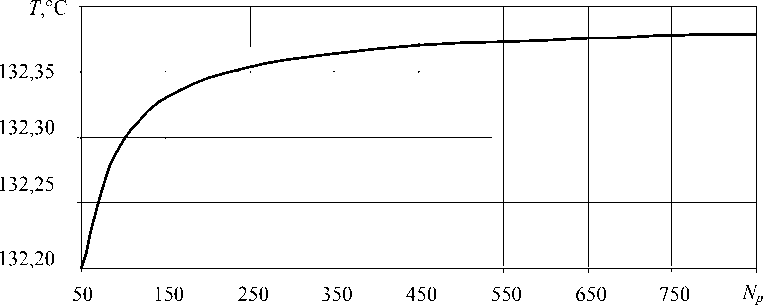
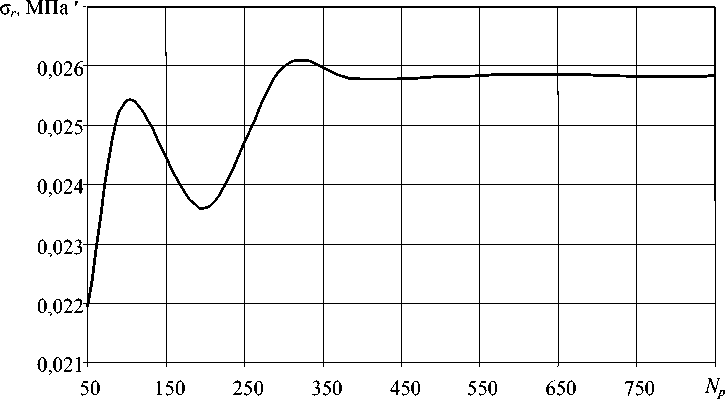
Для анализа практической сходимости конечно-разностного решения произведены расчеты кабеля марки КПБП 3 ^х 10 с водяным охлаждением (Табл. 1) при различном числе узлов как по осевой, так и по радиальной координате. В таблице обозначено: L_c — длина секции охлаждающей ванны. Наибольшая зависимость величин температуры и компонент тензора напряжений от степени сгущения сетки наблюдается в точке на границе раздела жилы и изоляции. При этом максимальная относительная погрешность решения для 400 и 800 узлов по радиальной координате при вычислении температуры и радиального напряжения в узле на границе раздела составляет менее 2 - 10 - ⁴ и 3 - 10 - ⁴ соответственно. Из рисунка 3 видно, что, начиная примерно с N p = 400, происходят незначительные изменения температуры и радиального напряжения при дальнейшем сгущении сетки в радиальном направлении.

Таблица 1. Варианты производственных режимов охлаждения изолированного провода

Марка кабеля	Диаметр жилы, мм	Линейная скорость, м/мин	Способ охлаждения изолированной жилы			Количество слоёв изоляции и их толщина, мм	Общая толщина изоляции, мм
			1 секция; L с , м	2 секция; L с , м	3 секция; L с , м
КПБП 3×10	3,65	35	Вода 80ºС; 10 м;	Вода 60ºС; 10 м;	Вода 20ºС; 7 м;	1×1,5	1,5
КПБП 3×16	4,56	20	Первый проход			1×1,5	1,5
			Вода 85ºС; 7,5 м	Вода 60ºС; 7,5 м	Вода 20ºС; 21,44 м
		20	Второй проход			1×1,5	3,0
			Вода 90ºС; 7,5 м	Вода 60ºС; 7,5 м	Вода 20ºС; 40 м

а

б

Рис. 3. Зависимость температуры и радиального напряжения в точке изоляции на длине охлаждающего участка 2,2 м в месте контакта с жилой от числа узлов конечно-разностной сетки в радиальном направлении Np при Nz = 400, Nm = 50

Максимальная относительная погрешность решения для 400 и 800 узлов по осевой координате при вычислениях температуры и радиального напряжения на границе раздела жилы и изоляции не превышает 5 - 10 - ³. Из рисунка 4 видно, что, начиная с N z = 400, значения температур, вычисленных на более мелких сетках, практически не отличаются. При дальнейших расчетах используется сетка N z = 400, N p = 400, N m = 50, при этом соотношение шагов по радиальной и осевой координатам для металла и полимера составляет h / h„ = 10 4 , h / h„ = 10 ^{- 5}. zm    zp

Основные аспекты построения разностных схем и алгоритмов решения полученных систем алгебраических уравнений подробно рассматриваются в работе [3].

Целью численного исследования являлось определение закономерностей процесса охлаждения и критериев, позволяющих предсказывать образование каверн, и, в связи с этим, выбор наиболее рационального режима охлаждения с точки зрения качества изоляции и увеличения производительности технологической линии.

На производстве приняты представленные в таблице 1 технологические режимы водяного охлаждения изолированного провода, входящего в состав кабеля КПБП. Невысокие величины скоростей изолирования и ограничение по толщине накладываемой изоляции (1,5 мм) обусловлены теплофизическими процессами, протекающими при изолировании, и требованиями, предъявляемыми к сплошности изоляции (отсутствием каверн).

Результаты численного исследования различных режимов охлаждения для проводов четырёх марок кабеля представлены в таблице 2. При этом использованы следующие обозначения: S — площадь поперечного сечения жилы; d — диаметр жилы; L воз — длина воздушной части секции; L — общая длина ванны; h — толщина изоляции. Вынужденное воздушное охлаждение проводится в трубе диаметром 100 мм со скоростью воздушного потока 6,8 м/с, направленного против движения провода.

Первый вариант соответствует реальному режиму охлаждения провода марки кабеля КПБП 3×10 (Табл. 1), используемому на предприятии ОАО «Камкабель» (г. Пермь). Варианты 3, 5, 6 — это экспериментальные режимы, проверенные на действующем оборудовании этого же предприятия (проведено более 20 экспериментов). Варианты, отмеченные звездочкой (2, 4, 7), представляют собой результаты численного эксперимента для воздушно-водяного режима охлаждения в ванне, конструкция которой представлена на рисунке 1. В вариантах 1–4 жила выполнена из меди, в вариантах 5–7 — из алюминия.

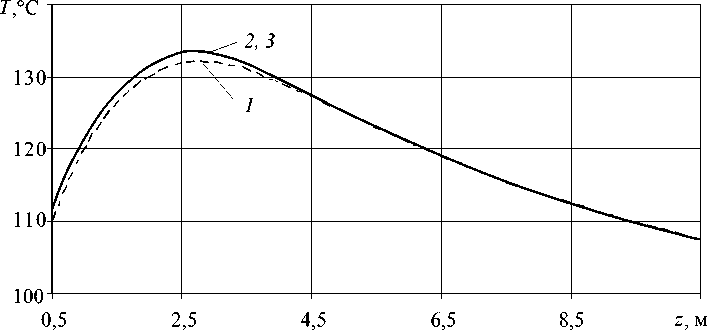
Рис. 4. Распределение температуры изоляции в месте контакта с жилой T ( R _ж , z ) по длине охлаждающего участка при N_p = 400, N_m = 50: кривая 1 – N_z = 100; кривая 2 – N_z = 400; кривая 3 – N_z = 1200

Таблица 2. Экспериментальные режимы охлаждения изолированного провода

№ варианта	S , мм 2	T ж , ºС	T из , ºС	d , мм	V , м/мин	Способ охлаждения изолированной жилы			L , м	h , мм	Наличие каверн в изоляции
						1 секция; L с , м; L воз, м;	2 секция; L с , м; L воз, м;	3 секция; L с , м;
1	10	80	240	3,65	35	Вода 80ºС; 10; 0	Вода 60ºС; 10; 0	Вода 20ºС; 7	27	1,5	нет
2*	10	80	240	3,65	45	Вода 75ºС; 11; 8	Вода 65ºС; 6; 2	Вода 30ºС; 10	27	1,5	нет
3	16	80	240	4,56	20	Вода 70ºС; 7,5; 0	Вода 45ºС; 7,5; 0	Вода 20ºС; 40	55	3,0	есть
4*	16	80	240	4,56	25	Вода 90ºС; 6; 2	Вода 80ºС; 27; 22	Вода 30ºС; 27	60	3,0	нет
5	16	20	240	4,42	16	Вынужденное воздушное; 14,54	Естественное воздушное; 44,32		58,86	3,0	нет
6	16	20	240	4,42	30	Вынужденное воздушное; 14,54	Естественное воздушное; 26,88	Вода 42ºС; 13,7	55,12	3,0	есть
7*	16	80	240	4,42	25	Вода 90ºС; 6; 2	Вода 80ºС; 27; 22	Вода 30ºС; 27	60	3,0	нет

На рисунках 5–6 приведены результаты численного моделирования полей температур провода и степени кристалличности в полимере при задании различных вариантов охлаждения провода (Табл. 2).

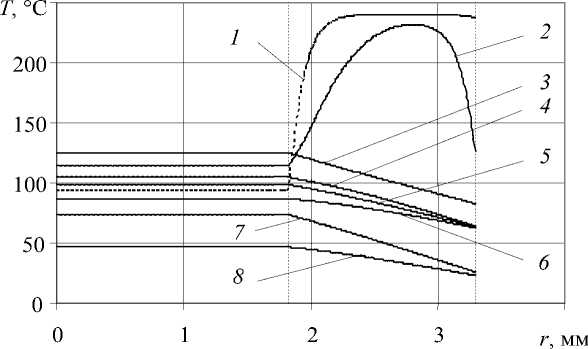
Характерное распределение температуры и степени кристалличности по радиусу в различных сечениях по длине провода для 1-го варианта представлены на рисунке 5. Видно, что температура в жиле мало изменяется по радиусу в связи с большой теплопроводностью металла, в то время как в изоляции на первых метрах охлаждения она претерпевает значительные изменения.

При температуре полимера ниже температуры плавления (Рис. 5, а , кривая 3 ) начинается процесс кристаллизации, который постепенно захватывает внутренние слои (Рис. 5, б , кривая 3 ).

На рисунке 5 показано, что в изоляции точки с различным радиусом имеют свою скорость охлаждения и, соответственно, степень кристалличности, увеличивающуюся с уменьшением скорости охлаждения. Так на участке охлаждения 5–13 метров (Рис. 5, а , кривые 3 , 5 ) центральные слои охлаждаются со 103 до 83ºС. В этом случае степень кристалличности увеличивается с 0,031 до 0,224 (Рис. 5, б , кривые 3 , 5 ), в то время как внешние слои, охладившись с большей скоростью до температуры 83ºС (Рис. 5, а , кривая 3 ), имеют кристалличность в 1,74 раза меньшую и равную примерно 0,129 (Рис. 5, б , кривая 3 ).

Степень кристалличности выше и при более длительном пребывании изоляции в температурном диапазоне максимального изменения β (рассматриваемый диапазон зависит от скорости охлаждения полимера и, в общем случае, находится приблизительно между 50 и 118°С) [3]. Так, несмотря на высокую скорость охлаждения, внешние слои (Рис. 5, б , кривая 8 ) в конце ванны имеют большую степень кристалличности, чем внутренние слои. Это объясняется тем, что при соответствующей скорости охлаждения

a

б

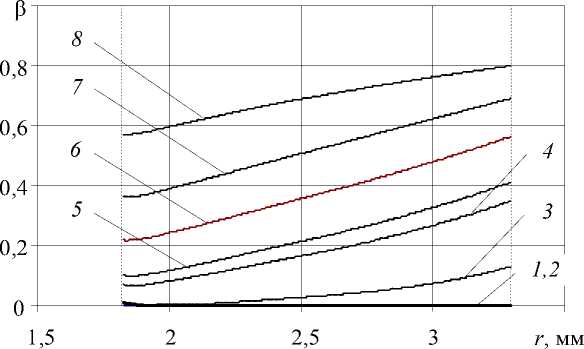
Рис. 5. Изменение температуры ( а ) и степени кристалличности полимера ( б ) по радиусу в различных сечениях по длине провода z (м) для 1-го варианта охлаждения (Табл. 2):

1 – z = 0,069; 2 – 0,623; 3 – 4,911 4 – 11,483; 5 – 13,074; 6 – 17,501; 7 – 22,135; 8 – 27,6

температурный диапазон максимального изменения β совпадает с диапазоном, в котором внешние слои находятся в течение времени, достаточного для увеличения β до значения 0,8 (Рис. 6, б , кривая 3 ).

Исследуя кривую 3 рисунка 6, а и сопоставляя ее с кривой 3 рисунка 6, б , можно заметить, что условия теплообмена внешних слоев изоляции, охлаждаемых в воде с температурой 80ºС, изменяют β этих слоев от 0 до ≈ 0,31. Дальнейшее охлаждение в воде с температурой 60ºС приводит к изменению от ≈ 0,31 до ≈ 0,64, причем время нахождения внешних слоев в воде при обеих температурах одинаково (Табл. 2). Из анализа кривых, изображенных на рисунках 5 и 6 видно, что максимальное изменение β во внешних слоях происходит в диапазоне от 60 до 88ºС, во внутренних слоях — в диапазоне от 50 до 95ºС.

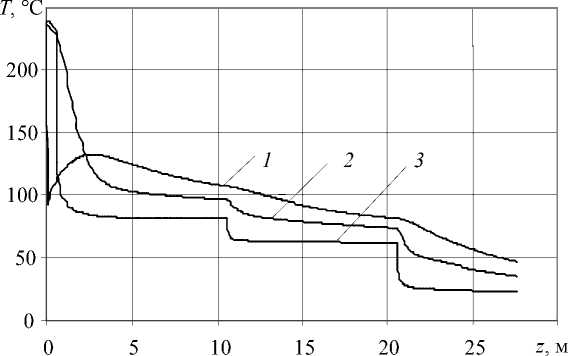
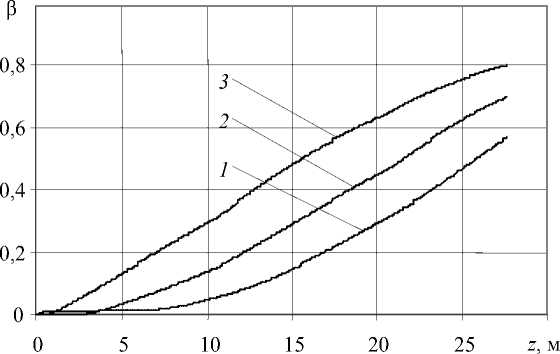
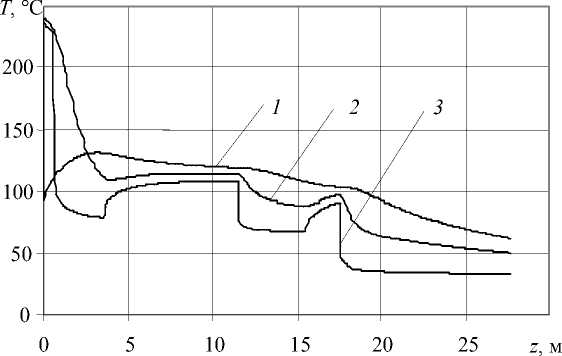
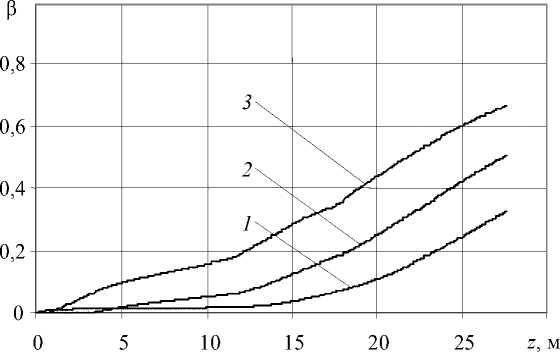
В случае воздушно-водяного охлаждения (2-й вариант Табл. 2) характер кривых зависимости степени кристалличности и температуры по длине водяного участка охлаждения существенно не меняется в сравнении с 1-м вариантом (полностью водяное охлаждение). Но на участках воздушного охлаждения наблюдаются некоторые особенности.

Значения температуры по толщине изоляции с продвижением провода вдоль воздушного промежутка стремятся к значению температуры ПЭНД в месте контакта с жилой (Рис. 6, в , кривые 2, 3 ). Это объясняется тем, что воздух обладает малой (по сравнению с водой) теплопроводностью и, как следствие, коэффициент теплоотдачи принимает небольшие значения. За счет этого при прохождении проводом воздушного промежутка тепло от внутренних слоев изоляции и жилы накапливается у поверхности провода, нагревая внешние слои, выравнивая температурное поле в изоляции.

а

б

Рис. 6. Эволюция по длине провода температуры T и степени кристалличности в изоляции β при 1-м ( а , б, ) и 2-м ( в , г) вариантах охлаждения.

1 - при r = R ж ; 2 - в точках изоляции r = R ж + 2 ( R _из - R ж ) ; 3 - r = R _из

в

г

Рис. 6. ( Продолжение )

Анализ всех вариантов воздушно-водяного охлаждения выявил две общие закономерности:

• •    во время прохождения провода через воздушные промежутки температура изоляции выравнивается по толщине;

• •    на воздушных участках охлаждения за счет повышения температуры внешних слоев изоляции наблюдается уменьшение скорости кристаллизации ПЭНД и, как следствие, снижение средней по радиусу степени кристалличности.

Таким образом, воздушно-водяное охлаждение, с одной стороны, обеспечивает уменьшение градиента температур в изоляции, являющегося основной причиной возникновения напряжений; с другой, — приводит к снижению средней степени кристалличности по радиусу изоляции по сравнению с обычным (водяным) охлаждением.

На втором этапе решения поставленной задачи на основании математической модели, описывающей напряженно-деформированное состояние изолированного провода (10)–(17), а также полученных температурных и кристаллизационных полей для ряда вариантов охлаждения провода (Табл. 2) получены поля перемещений, радиальных и окружных напряжений. Для выбора критерия, характеризующего потерю сплошности материала (образование каверн), в работе совместно рассмотрены поля температур, кристаллизационные поля и поля радиальных напряжений.

Характерное изменение температуры, степени кристалличности и радиальных напряжений в полимере по радиусу в различных сечениях по длине охлаждающей ванны представлено на рисунке 7 для 1-го варианта охлаждения провода (Табл. 2).

На начальном этапе охлаждения на длине 2,35 м в изоляции по всей толщине возникают значительные сжимающие напряжения (кривая 3 , Рис. 7, а ) за счет возрастания температуры жилы до 134ºС и, соответственно, ее расширения, а также за счет усадки внешних слоев изоляции вследствие их резкого охлаждения в воде. Дальнейшее охлаждение внешних слоев приводит к росту степени кристалличности по всей толщине изоляции, при этом кристалличность внешних слоев превышает кристалличность внутренних.

Совместное деформирование относительно жестких наружных и менее жестких внутренних, испытывающих структурную усадку слоев приводит в дальнейшем к образованию растягивающих радиальных напряжений во внутренних слоях (кривая 3 , Рис. 7, б ). Из рисунка 7 видно, что растягивающие напряжения в месте контакта изоляции и жилы возникают на фоне небольшой ( β ≤0,08) кристалличности полимера. Эти напряжения также незначительны и не способны привести к возникновению каверн.

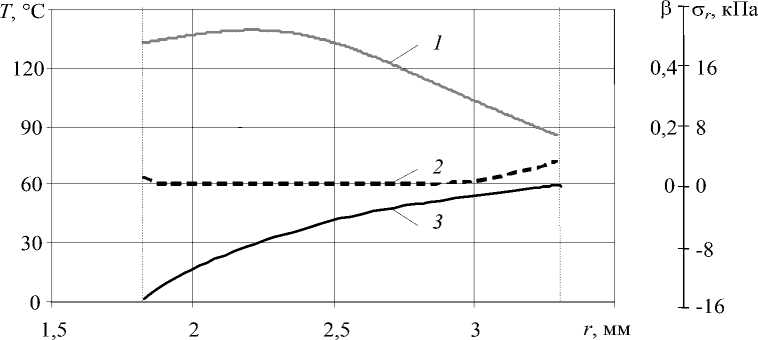
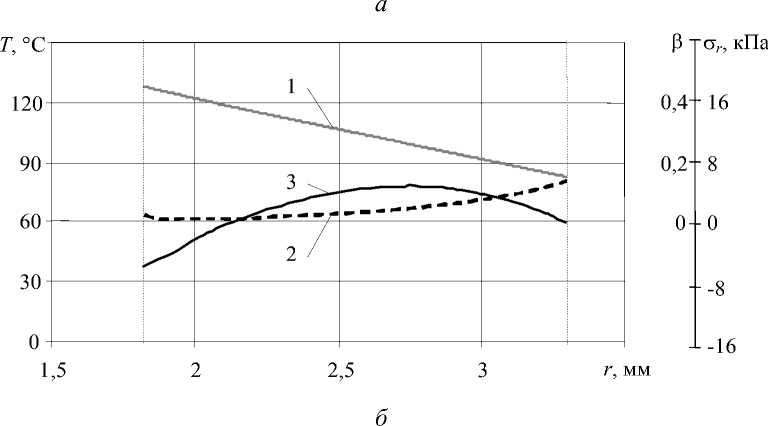
Рис. 7 . Изменение температуры (кривая 1 ), степени кристалличности (кривая 2 ) и радиальных напряжений (кривая 3 ) по радиусу изоляции при 1-м варианте охлаждения (Табл. 2) на расстоянии z (м) от начала участка охлаждения: а – z = 2,35; б – 4,36; в – 5,40

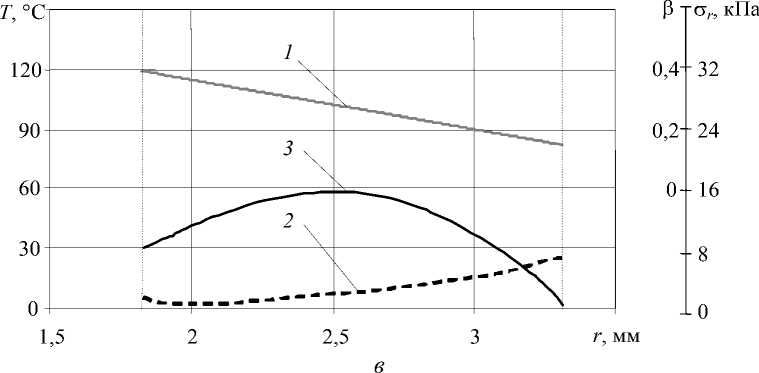
Рис. 7 . ( Продолжение )

В связи с этим особый интерес представляет поведение радиальных напряжений на внутренней поверхности изоляции и фазовое состояние полимера в данной области провода. На рисунке 8 представлены изменения температуры, степени кристалличности и радиальных напряжений в полимере по длине охлаждающего участка в точках контакта жилы и изоляции для 2–7-го вариантов охлаждения провода (Табл. 2).

Во 2-м варианте режим охлаждения является воздушно-водяным. Как видно из рисунка 8, а , растягивающие напряжения в изоляции возникают в момент достаточной закристаллизованности полимера (степень кристалличности составляет около 0,03) и не достигают высоких значений, способных привести к образованию пустот. Скорость наложения изоляции по сравнению с 1-м вариантом выше на 10 м/мин, что говорит о предпочтительности применения 2-го варианта режима охлаждения.

В 3-м варианте на расстоянии 8,5 м от начала охлаждения во внутренних слоях изоляции начинают появляться и резко возрастать растягивающие напряжения; при этом полимер находится в расплавленном состоянии (Рис. 8, б ). Вероятно, это обстоятельство и является причиной образования каверн в месте контакта материалов провода.

В 4-м варианте опробован режим воздушно-водяного охлаждения для провода с толщиной изоляции 3 мм. Из рисунка 8, в видно, что на расстоянии 32 м от начала участка охлаждения при попадании провода в секцию с водой в месте контакта жилы и изоляции появляются растягивающие напряжения. Однако к этому моменту полимер уже начинает кристаллизоваться на внутренней поверхности изоляции (β = 0,027), и появление каверн маловероятно.

Предложенный способ охлаждения гораздо эффективнее применяемого в настоящее время на производстве (Табл. 1), так как наложение изоляции производится в один проход и с большей скоростью.

В 5-м варианте (Рис. 8, г ), охлаждение производится полностью на воздухе при малой скорости движения провода, поэтому температурное и кристаллизационное поля распределяются по радиусу более равномерно, чем при охлаждении в воде. Как следствие, растягивающие радиальные напряжения в жиле появляются уже после того, как β достигает значения 0,06, достаточного для выполнения условия отсутствия каверн. Использование 5-го варианта охлаждения на производстве недопустимо, так как средняя температура изоляции в конце охлаждающей ванны едва достигает 100ºС. При такой температуре нельзя производить смотку провода на барабан, так как возможно слипание, сминание изоляции и смещение жилы относительно оси провода. Для реализации режима воздушного охлаждения необходимо или значительно снижать скорость провода, или повышать длину охлаждающего участка, что неэкономично.

В 6-м варианте (рис. 8, д ) применялась более высокая, по сравнению с 5-м вариантом, скорость изолирования и водяное охлаждение в конце воздушной секции. Эти отличия и предопределили появление каверн на внутренней поверхности изоляции. При попадании провода в секцию с водой из-за резкого перепада температур начинается интенсивная кристаллизация и усадка внутренних слоев изоляции на фоне более жестких (закристаллизовавшихся) слоев на поверхности и расплавленных, прилегающих к жиле. Это вызывает возникновение и рост растягивающих радиальных напряжений и, как следствие, образование каверн на внутренней поверхности изоляции.

Седьмой вариант охлаждения (Рис. 8, е ) полностью аналогичен четвёртому, отличие лишь в материале жилы: в 7-м варианте изоляция накладывается на алюминиевую жилу, а в 4-м — на медную. Характер кривых температуры, степени кристалличности и радиальных напряжений практически не отличается (Рис. 8, в и е ), и каверны в изоляции так же не должны появиться. Предложенный вариант рекомендован для применения на производстве.

По результатам проведенных натурных экспериментов для 3-го и 6-го вариантов установлено наличие каверн на внутренней поверхности изоляции (в месте контакта полимера с жилой); в 1-м и 5-м вариантах дефекты в изоляции не обнаружены. Анализ численных исследований полей радиальных напряжений и степени кристалличности позволяет отметить, что для 3-го и 6-го вариантов режимов охлаждения, во внутренних слоях изоляции в моменты, когда степень кристалличности равна нулю (расплав полимера) устанавливаются достаточно высокие уровни растягивающих радиальных напряжений, которые, по-видимому, приводят к отслаиванию изоляции. В режимах 1 и 5 радиальное напряжение в расплаве полимера всегда сжимающее. И только после перехода расплава полимера в аморфно-кристаллическое состояние (степень кристалличности отлична от нуля) на внутренней поверхности изоляции возникают растягивающие радиальные напряжения.

Таким образом, для рассматриваемого в данной работе провода практическим критерием неудовлетворительного режима охлаждения можно считать появление растягивающих напряжений в зонах с нулевой степенью кристалличности. Анализ результатов численных исследований остальных экспериментальных режимов подтверждает правильность выбора этого критерия, предсказывающего образование каверн.

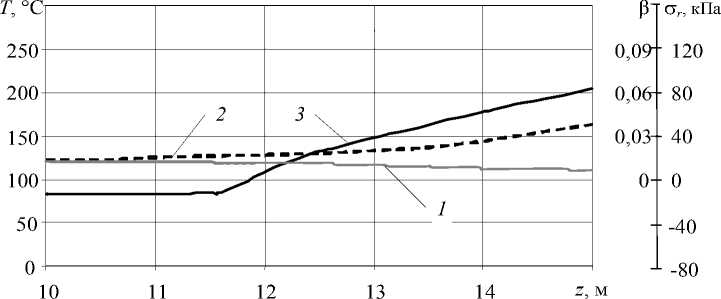
а

Рис. 8. Изменение температуры (кривая 1), степени кристалличности (кривая 2) и радиальных напряжений (кривая 3) в месте контакта жилы и изоляции по длине охлаждающей ванны для различных вариантов охлаждения (Табл. 2):

а – 2-й вариант; б – 3-й; в – 4-й; г – 5-й; д – 6-й; е – 7-й

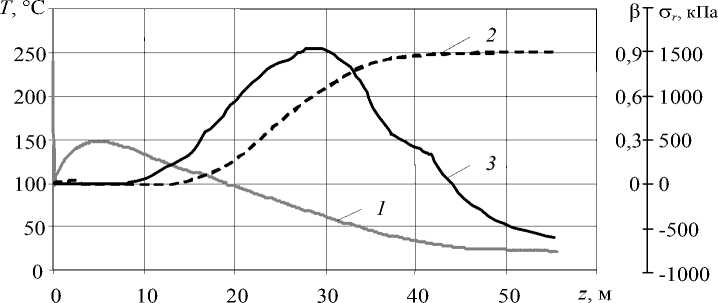
б

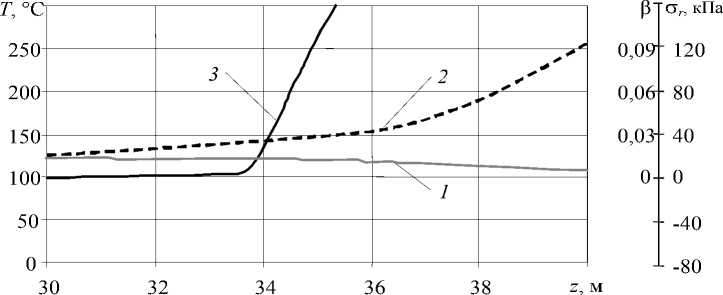
в

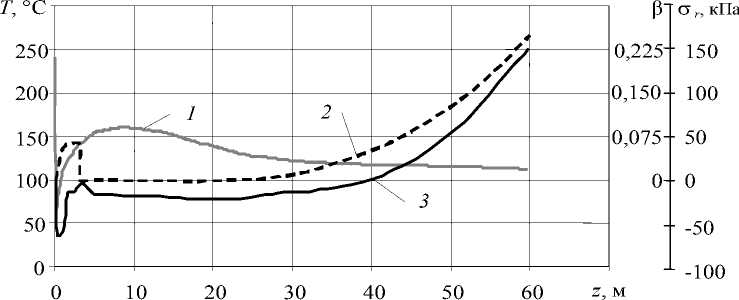
г

Рис. 8. ( Продолжение )

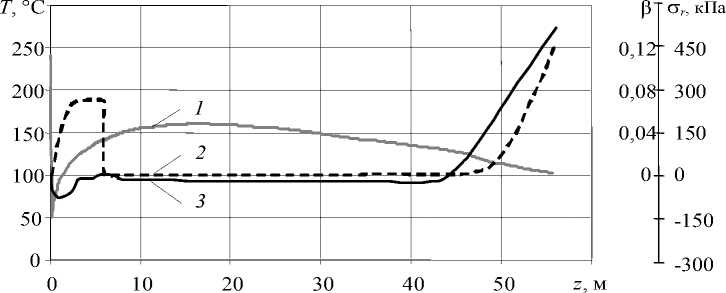
д

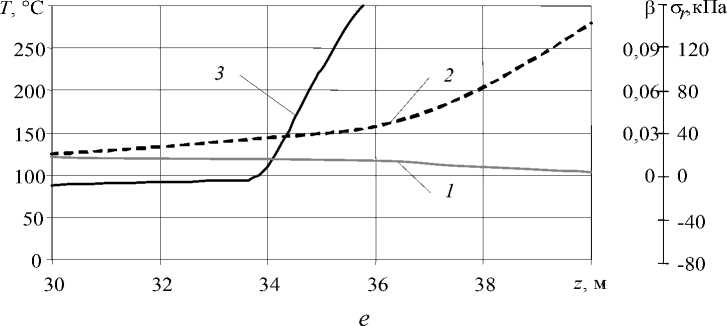
Рис. 8. ( Продолжение )

Предложенные в результате вычислительных экспериментов режимы воздушноводяного охлаждения (варианты 2, 4, 7) позволяют избежать возникновения радиальных растягивающих напряжений в критических зонах изоляции и при этом увеличить скорость изолирования на 25–30 %.