Численное моделирование термомеханического поведения аморфно-кристаллических полимеров с памятью формы

оборудовании, микроэлектронике, космической индустрии и некоторых других отраслях техники, поэтому различным аспектам, связанным с SMP, в последнее время посвящено большое число публикаций, в том числе обзорного характера [2–5]. Большинство исследований, объектом которых являются SMP, сосредоточено на экспериментальных изысканиях, включая разработку новых химических составов, проявляющих свойства памяти формы, и проектирование устройств для новых приложений. Относительно небольшое их число связано с математическим моделированием эффекта памяти формы.

Настоящая работа посвящена термомеханическому моделированию эффекта памяти формы в аморфно-кристаллических полимерах. Здесь он определяется релаксационным переходом, наблюдающимся в аморфной фазе в диапазоне температур, включающем температуру стеклования T_g , и представляется в виде термомеханического цикла. Термомеханическим циклом памяти формы обычно называют эволюцию напряжений, деформаций и температуры на этапах создания и сохранения некоторого деформированного состояния тела с последующим восстановлением его первоначальной формы.

При математическом моделировании термомеханических циклов памяти формы, как правило, используются два подхода. Первый из них ограничивается рамками стандартной линейной вязкоупругости и заключается в моделировании SMP в виде сочетания упругих и вязких элементов с параметрами, зависящими от температуры [6–8]. Второй (общий) подход основывается на изучении термодинамических аспектов эффекта. Считается, что в первую очередь эффект определяется переходом от высокоэластического состояния (характеризующегося температурой выше температуры T_g ) к застеклованному (ему соответствует температура ниже T_g ) вследствие изменения сегментарной подвижности полимерных цепочек. В рамках этой общей концепции разными исследователями используется подход, в котором SMP представляется в виде смеси двух фаз: жесткой, замороженной и мягкой, активной. Переход от одного состояния к другому моделируется как изменение относительных долей объема этих фаз, для чего вводится переменная состояния (как правило, доля одной из фаз). Построенная модель представляется в терминах термомеханики и используется для описания поведения материала с памятью формы путем решения определяющих уравнений [9–16].

Предлагаемый в настоящей работе метод моделирования эффекта памяти формы также можно отнести ко второму (общему) подходу, поскольку он базируется на определяющих соотношениях. Ранее авторами данной статьи был разработан вариант определяющих соотношений для описания термомеханического поведения аморфнокристаллических полимеров в широком температурном диапазоне [17]. В отличие от двухфазной модели с переменной состояния, предложенная модель является более общей и способна описывать не только память формы, но и другие термомеханические эффекты, наблюдаемые при деформировании аморфно-кристаллических полимеров [17]. Полимерный материал рассматривается как двухкомпонентная смесь аморфной и кристаллической структур, удельная доля которых зависит от степени кристаллизации β . Для определения величины β , характеризующей долю закристаллизовавшейся структуры, используются кинетические уравнения кристаллизации, вид которых обусловливается типом процесса кристаллизации [18]. Предполагается, что каждая часть аморфной структуры полимера, пропорциональная приращению степени кристаллизации Δβ , в момент перехода в кристаллическое состояние имеет нулевые напряжения и согласована по деформациям с ранее существовавшей структурой.

Выражение для удельной свободной энергии двухкомпонентной системы записывается в виде:

p ( t )

F[8(t),T(t)] = J Fc [8(tH(t),T(t)]dP(t) + Fa [s(t),T(t)](1 -₽(t)),             (1)

где F_c — удельная свободная энергия кристаллической структуры; F_a — удельная свободная энергия аморфной структуры; s ( t ) — тензор деформации, T ( t ) — текущая температура. Задавая конкретный вид F_c и F_a , можно получить определяющие соотношения:

• ° Л t ) = ^d F / ^ds ij- ⁽²⁾ Аморфным полимерам соответствует вариант при р ( t ) = 0. Предложенные определяющие соотношения позволяют учесть влияние на напряженно-деформированное состояние полимерного материала как фазовых превращений, так и релаксационных переходов типа стеклования (в аморфной составляющей).

Для характеристики на феноменологическом уровне эволюции межмолекулярного взаимодействия полимерных цепочек аморфной составляющей материала вводятся тензорные величины e ij , s kk , и с их учетом записываются выражения для удельной свободной энергии аморфной и кристаллической компонент в виде:

• ^Fa [ ⁸ ( t ) , ^{T (} t ) ] = Н 1 e ij e ij/^ ⁺ Ц 2 ⁽ e ij ^— e ij ⁾⁽ e ij ^— e ij ) /^{2 + k} 1 ⁸ kk /^{2 + k} 2 ( ⁸ kk ^{— 8} kk ) /^{2 —}

• ^{— ( k} 1 ^{+ k} 2 ) ' ^a a " ^{( T — T} 0 ) " ^£ kk , ⁽³⁾

Fc [s (t), T(t)] = Gce,e,l2 + Bc8* /2 — Bc' “c" (T — To)' = k. - где p1, k1 и p2, k2 — сдвиговой и объемный модули, характеризующие упругие свойства аморфной составляющей материала в высокоэластическом состоянии и упругие свойства, обусловленные межмолекулярным взаимодействием полимерной сетки; ey — компоненты девиатора тензора деформации; skk — объемная деформация; Gc, Bc — сдвиговой и объемный модули кристаллической компоненты материала; a a, а c — коэффициенты температурного расширения аморфной и кристаллической составляющих соответственно; T0 — температура окружающей среды.

Тогда определяющие соотношения принимают вид:

5 F ^Р ( t )

sij = "7 = J 2Gc [eij (t) — eij (t)] dP (t) + [^1 eij + ^2 (eij — eij (1 — P (t)) -

• d eij0

№ ^p ( t )

• °» = 3= J {3Bc [sk, (t) —8„ (t)] — 3Bcac[T(t) — T(t)]} d₽(t)+(4)

dS kk0

+ [3 k18 kk + 3 k2 (8 kk —8kk ) — 3 (k1 + k2 )a a [ T ( t ) — T0 ]](1 — P( t )) - где sij, °kk — компоненты девиатора и первый инвариант тензора напряжения.

Компоненты тензоров e *., s ,. характеризуют деформационное состояние, относительно которого на текущих деформациях e_y , s _kk проявляются жесткостные свойства возникающих в зависимости от энергетического состояния межмолекулярных связей. Эти связи могут переходить в новое равновесное состояние, которое определяется кинетическими соотношениями аррениусовского типа

• *        J eij = Aa exP

*

^s kk = A b exp

— u e -e e a 2 mn mn mn

Tk (T)

^Ub - ^k1 ( ^s kk - ^£*kk

Tk (T)

4 n )/¹

■ kk    ^S kk

*

ij ij

где U_a , U_b — величины, характеризующие энергию активации сегментарной подвижности полимерной сетки за счет физических связей межмолекулярного взаимодействия; T_k ( T ) — энергетическая температура, имеющая размерность Дж/м³; A_a , A_b — величины, обратно пропорциональные характерному времени перехода межмолекулярных связей в равновесное состояние.

Далее для модельного полимерного материала рассчитывался типичный термомеханический цикл, демонстрирующий эффект памяти формы в случае однородного напряженно-деформированного состояния. Рассматривался вариант силового нагружения — задавался характер изменения напряжения: о x = о x ( t ) . Все остальные компоненты тензора напряжений принимались равными нулю. При численном моделировании процессов однородного нестационарного деформирования исследуемого материала задача сводилась к решению системы шести уравнений. Три интегральных уравнения для определения компонент тензора деформации s x ( t ) , s y ( t ) , s z ( t ) были получены из соотношений (4), и три дифференциальных уравнения для компонент тензора s * — из кинетических уравнений (5). Для проведения численных экспериментов был использован пошаговый алгоритм, согласно которому путем аппроксимации интегралов конечной суммой интегральные уравнения приводились к линейным алгебраическим уравнениям [19], а для решения дифференциальных уравнений на каждом шаге по времени применялся метод Рунге–Кутты четвертого порядка.

Начальные условия для кинетических уравнений принимались нулевыми, так как материал был предварительно недеформированным и в начальный момент находился в состоянии высокоэластичности.

Поскольку моделировался эффект памяти формы, связанный с релаксационным переходом в аморфной фазе в диапазоне температур, включающем температуру стеклования T g , для определенности было принято в ( t ) = 0, то есть полимер считался полностью аморфным. На рисунке 1 показано изменение во времени заданных силовых и температурных нагрузок для моделируемого цикла памяти формы.

б

0         40         80    /, мни

а

0          40         80    /, мин

Рис. 1. Изменение во времени заданных силовых ( а ) и температурных ( б ) нагрузок

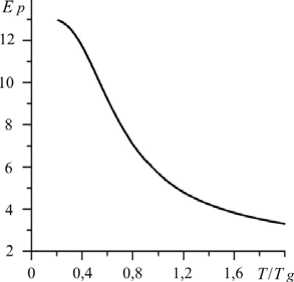
Рис. 2. Зависимость модуля от температуры в зоне релаксационного перехода

В расчетах были приняты следующие значения входящих в уравнения термомеханических характеристик: р 1 = 1; к 1 = 4,667; ц ₂ = 10; к 2 = 93,33; U a = 3,0 - 10 ^{- 5} Дж/м³; U b = 1,0 - 10 ^{- 3} Дж/м³; A_a = 1,0 сек ^{- 1}; A b = 0,1 сек ^{- 1}; a a = 1,0 - 10 ^{- 5}. Компоненты напряжений были приведены к безразмерному виду путем деления на величину модуля р 1 , а энергетическая температура задавалась в виде линейной функции температуры T_k = ( p + qT ( t ) ) - 10 ^{- 5}, где p = - 1,533, q = 0,0327 (V град ) , что обеспечивало безразмерность показателей экспонент в кинетических уравнениях.

На рисунке 2 показана расчетная зависимость приведенного модуля E_p = 3 о x /[ ( е x -0 )/( 1 +v ) +0/ ( 1 - 2 v ) ] от отношения TT_g для модельного полимера. Кривая демонстрирует характер поведения, типичный для реальных стеклующихся полимерных материалов. Здесь 0 — объемная деформация, v — коэффициент Пуассона.

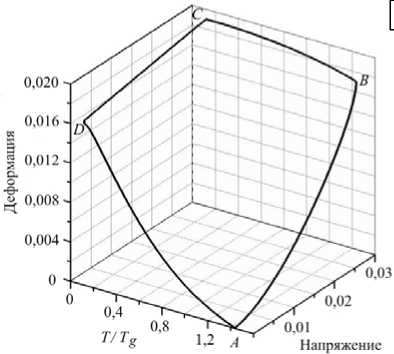
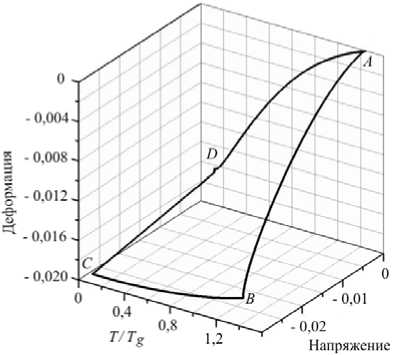
На рисунке 3 приведены результаты моделирования термомеханического цикла со свободным восстановлением формы для двух случаев предварительного деформированного состояния модельного материала — одноосного растяжения и одноосного сжатия. Первоначально материал находился в высокоэластическом состоянии и имел температуру выше температуры релаксационного перехода (T/Tg > 1); на рисунке это соответствует точке А. Затем материал деформировался без изменения температуры и переходил в состояние, обозначенное точкой В. Последующее охлаждение до температуры ниже температуры стеклования (T[Tg < 1) при условии постоянства напряжения переводило материал в застеклованное состояние, в точку С. После разгрузки при этой температуре деформация практически оставалась такой же (точка D), как и в состоянии С, и могла сохраняться без изменения неограниченно долго. Восстановление формы, то есть переход в первоначальное состояние (точка А) достигалось путем нагревания до первоначальной температуры без каких-либо ограничений на деформации. При необходимости такие циклы (A ^ B ^ C ^ D ^ A) могли повторяться. Следует отметить, что возврат в точку А (то есть замыкание цикла) обеспечивалось тем, что характерные времена изменения нагрузок и температуры (Рис. 1) были намного больше характерных времен релаксации (Aa-1, Ab-1).

а

б

Рис. 3. Эволюция термомеханических параметров в течение цикла памяти формы для двух случаев предварительного деформированного состояния: одноосное растяжение ( а ) и одноосное сжатие ( б )

Таким образом, проведенные расчеты показали, что система определяющих уравнений, разработанная для описания термомеханического поведения аморфнокристаллических полимеров в широком температурном диапазоне, и кинетические уравнения для определения тензорных величин, характеризующие эволюцию межмолекулярного взаимодействия, позволяют моделировать термомеханические циклы памяти формы. Полученные результаты демонстрируют качественное соответствие деформационных процессов модельного материала поведению реальных полимеров, описание которого приведено, например, в работе [9].

Работа выполнена при финансовой поддержке РФФИ (проекты № 10-01-96032 р_Урал_а, № 09-08-01020-а)