Численное моделирование трехмерных нестационарных течений и тепломассопереноса в цилиндрическом жидком мостике при отсутствии силы тяжести

Перспективным способом получения монокристаллов полупроводников является выращивание их методом плавающей зоны, позволяющим избежать загрязнения расплава материалом тигля. Реализация процесса в условиях микрогравитации исключает гравитационную конвекцию. Однако даже в этом случае в расплаве имеет место тепловая и концентрационная конвекция Марангони. При достаточной интенсивности движения устанавливается колебательный режим, приводящий к нежелательной неоднородности выращиваемого кристалла. В силу непрозрачности расплавов полупроводников экспериментальное изучение течений в них является сложным, и особый интерес приобретает численное моделирование.

В литературе имеется большое число работ, посвященных изучению термокапиллярной конвекции при выращивании кристаллов методом плавающей зоны. Теоретическое исследование общих свойств осесимметричного термокапиллярного

течения в цилиндрическом жидком мостике в предельном случае малых чисел Рейнольдса и Марангони проведено в работе [1]. Здесь решение системы уравнений для функции тока, завихренности и температуры получено в виде рядов. Численное моделирование течений, теплопереноса, формы свободной поверхности и фронтов плавления и кристаллизации выполнено в работах [2], [3]. Система уравнений и граничных условий дискретизировалась методом конечных объемов и решалась методом Ньютона. Вычисления проводились для нитрата натрия с числом Прандтля 9–12 и для кремния с числом Прандтля 0,01 . Расчеты позволили изучить структуру течения, положение и форму свободной поверхности и фронтов плавления и кристаллизации. Полученные данные оказались в хорошем согласии с результатами, наблюдаемыми в эксперименте.

Трехмерное численное моделирование стационарных термокапиллярных течений в жидкой зоне с учетом плавления и кристаллизации, искривления свободной поверхности и отклонения формы растущего кристалла от осевой симметрии выполнено в работе [4]. Рассматривалась двухэллипсоидная зеркальная печь. Установившийся рост кристалла иттрий-алюминиевого граната использовался в качестве примера для иллюстрации сложной взаимосвязи между конвекцией и формами свободной поверхности и фронтов фазовых переходов.

В работе [5] описаны эксперименты по выращиванию кристаллов германия с примесью кремния методом плавающей зоны при помощи моноэллипсоидальной зеркальной печи. Воспроизводимо удавалось выращивать монокристаллы с концентрацией примеси до 10% с использованием заранее выращенной поликристаллической заготовки с заданным распределением концентрации. Наблюдалась зависимость макроскопической неоднородности кристалла (излома фронта кристаллизации на некотором расстоянии от боковой поверхности) от концентрации кремния. Появление такой неоднородности только при наличии свободной поверхности позволило сделать вывод о ее обусловленности концентрационно-капиллярной конвекцией.

Концентрационно-капиллярная конвекция при выращивании кристаллов методом плавающей зоны изучена гораздо меньше, чем термокапиллярная конвекция. В работе [6] исследованы осесимметричные режимы концентрационно-капиллярной конвекции в изотермической жидкой зоне в условиях невесомости и изучена устойчивость осесимметричных режимов по отношению к трехмерным возмущениям, периодическим в азимутальном направлении. В [7] численно рассмотрено влияние сильного осевого магнитного поля на стационарные режимы термо- и концентрационно-капиллярной конвекции в жидкой зоне, подверженной действию силы тяжести. Обнаружено, что при некоторых значениях параметров сосуществуют два устойчивых стационарных режима: одновихревой — с доминированием концентрационно-капиллярного механизма генерации течения, и двухвихревой — с доминированием термокапиллярного механизма. Сосуществование этих режимов в случае, когда гравитационное и магнитное поля отсутствуют, исследовано в работе [8]. Прослежена эволюция конвективного течения при переменном тепловом и фиксированном концентрационном числах Марангони; найдены области бистабильности; изучена линейная устойчивость стационарных осесимметричных режимов конвекции относительно трехмерных возмущений, периодических в азимутальном направлении. Показано, что наличие даже слабого концентрационно-капиллярного эффекта сильно воздействует на устойчивость термокапиллярного течения, и, наоборот, наличие термокапиллярного эффекта сильно воздействует на устойчивость концентрационно-капиллярного течения.

Настоящая работа посвящена численному моделированию трехмерных нестационарных режимов течений термокапиллярного и концентрационно-капиллярного происхождения в жидком мостике в отсутствие силы тяжести. Одновременный учет обоих механизмов генерации течения позволяет рассмотреть принципиально иной по сравнению с изучавшимся в работе [4] класс решений (и получить более достоверные результаты даже в случае доминирования термокапиллярного механизма). Решение нестационарных уравнений движения и исследование нестационарных закритических режимов важно для прогнозирования свойств выращиваемого кристалла. Выбор значений параметров для изучения характерных режимов течения осуществлялся в соответствии с данными карт устойчивости, полученными в работе [8]. Интерес представляло как сопоставление с результатами анализа линейной устойчивости, так и изучение трехмерных надкритических, в том числе нестационарных, движений жидкости.

• 2.    Постановка задачи. Определяющие уравнения

Рассмотрим в цилиндрической системе с координатами ( г, ф , z ) жидкий мостик между фронтом кристаллизации растущего кристалла ( z = 0) и фронтом плавления заготовки ( z = L ) при выращивании монокристалла полупроводника методом плавающей зоны в условиях невесомости (Рис. 1). Мостик имеет форму кругового цилиндра c радиусом R и высотой H ( L — отношение высоты мостика к радиусу: L = H/R). Расплав нагревается посредством радиационного переноса энергии от кольцевого нагревателя с гауссовым распределением температуры, максимальное значение которой равно T 1 . Нагреватель расположен посередине между кристаллом и заготовкой, система «заготовка–жидкий мостик–кристалл» протягивается через него со скоростью u_cr . T ₀ — температуры плавления и кристаллизации. Поверхностное натяжение полагаем зависящим и от температуры, и от концентрации легирующей примеси в расплаве. Деформациями свободной поверхности ( r = R ) и кривизной фронтов плавления и кристаллизации пренебрегаем.

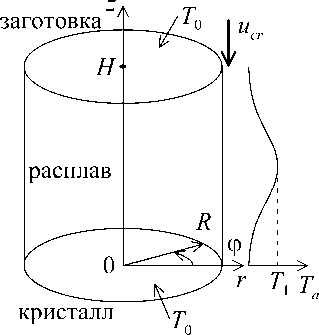
Рис. 1. Схема жидкого мостика и распределение по его высоте температуры нагревания

Уравнения для скорости й , давления p , температуры T и концентрации C в системе отсчета, связанной с кристаллом и заготовкой, имеют вид:

^ + ( ( й - V g й z > V ) й = -V p + Д й ,                                            (1)

Ц + (й - V., ) V T = ± Д Т,                                              (2)

dt                  Pr дс -            1

— + (й - V_e )VC = — AC, dt         g z Sc div u = 0.

Здесь и далее используются безразмерные величины для скорости, давления, концентрации примеси, температуры, времени и расстояния и введены, соответственно, следующие единицы измерения: v / R ; pv ² /R²; C f ; A T = T 1 - T ° ; R 2 / v , R ( v и p — кинематическая вязкость и плотность расплава, C f — концентрация примеси в заготовке). Также приняты обозначения: V_g — безразмерная скорость протяжки ( V_g = u_crR /v ); e . — единичный вектор, направленный вдоль оси . .

На твердых поверхностях скорость движения расплава обращается в нуль:

u = 0.

На свободной поверхности равна нулю нормальная компонента скорости:

U n = 0.

Условие для касательной компоненты тензора напряжений сдвига на свободной поверхности в силу наличия термокапиллярного и концентрационно-капиллярного эффектов записывается в виде:

П = Mar V T - Ma C V C . Pr ^T Sc ^T

Оператор V_T — это тангенциальная часть оператора градиента: V_T = т ( t V ) . Отклонениями свободной поверхности от цилиндрической формы пренебрегаем, поэтому запись условия баланса нормальных напряжений не требуется.

Граничные условия для температуры на фронтах

T| , = 0 = °.    T1 ..= L = °.

на свободной поверхности

= - Bi (T - T a ), o n

Ta = e

,- ( ( . - L/2)/ A h ) ²

где температурным профилем    T_a   моделируется кольцевой нагреватель;

A_h — характерная ширина нагревателя.

Граничные условия для концентрации на фронтах кристаллизации и плавления, соответственно, имеют вид:

| C = - ScV g ( 1 - k ° ) C , o n

;d C = ^{- S}c^Vg ( ^{C - 1 )} -

Здесь k0 — коэффициент сегрегации.

Поток примеси через свободную поверхность равен нулю:

⁶-C = 0.

d n

Задача характеризуется следующими безразмерными параметрами: числом Прандтля Pr = v/x ( X — коэффициент температуропроводности расплава), числом Шмидта Sc = v/ D ( D — коэффициент диффузии примеси в расплаве), числом Био Bi = sc * T 1 ³ R /x ( s — эффективный коэффициент теплопередачи, с * — постоянная Стефана-Больцмана), тепловым числом Марангони Ma_T = | с‘ | AT R/( pvx ) ( с Т = 5с / S T — коэффициент зависимости поверхностного натяжения расплава с от температуры) и концентрационным числом Марангони Ma _C = с' _C C_fR| ( p D v ) ( с С = 5с / d C — коэффициент зависимости поверхностного натяжения от концентрации примеси).

Обозначим компоненты вектора скорости в цилиндрической системе координат: u = ( u, v, w ) . Тогда уравнения (1)-(4) принимают вид:

d u     d u v du / --+ u --1----+ ( w - d t d r r дф '	V ^-11 = g’ d z    r	д р d 2u  1 d u 1 +    2 +     + 2 5 г   5 г    г d r r	d 2u	d 2u    u +--2---2 d z 2    r 2	2 d v
			дф 2		r 2 дф ,

d v    dv v d v /     ,, \ dv u • v

— + u— +--+ (w - V) — +--= dt    dr r дф g ’ dz   r

1 д р d ²v 1 d v 1 d ²v

---1 2 +----1—2--2 r дф d r    r d r r дф

д ²v v 2 д и + 5? " 7 ⁺ 7 дф,

d w	d w v dw /   T7 \ dw — +--+ ( w - V g )— = д г r дф         g^ 5 z S T v д Т ,       S t — +--+ ( w - V g )— = S r r 5ф v        5 z	д р	7 d 2 w 1 d w   1 d 2 w	d 2 w
--+ u			+ , +      + -    ,	I
d t S T		d z 1	d r2 r d r r 2 дф ' d 2T 1 S T 1 d 2T	d z2 d 2T )
--+ u d t		Pr	^ d r2 r d r r 2 дф 2	д 2   , d z J
d C	S C vSC /   TxdC --1----+ ( w - V g )— = d r r 5ф v        S z 1 d v dw „ +--+ — = 0 . r 5ф d z	1	( d 2C 1 d C   1 d 2C	d 2C )
--+ u		—	—+--I ,—. I—
d t S u u --1— 5 г   r		Sc	^d r2 r d r r 2 дф	d z2 J

Граничные условия записываются следующим образом:

- на фронте кристаллизации ( z = 0):

и = v = w = T = 0,     — = - ScV ( 1 - k ) C ;

g 0

- на фронте плавления ( z = L ):

r n дС

-

SV ( C - 1 ) ;

u = v = w = T = 0 ,    — dz

- на свободной поверхности ( r = 1):

dC  л dw   Ma7 ST  Ma rSC u = — = 0, — =---— + dr dr Pr  dz    Sc dv _Ma C dC MaT ST --v _-----, dr      Sc Эф Pr Эф

— _- Bi ( t - T ) . dr        ^v ’

Граничные условия для давления на фронтах плавления и кристаллизации и на свободной поверхности получаются путем проектирования уравнения Навье–Стокса на нормаль к границам:

d p d n

-

—* u

-

V g e_z ) v ) U— + k u ) .

• 3.    Генерация сетки

Задача дискретизируется методом конечных разностей на равномерной по азимутальной координате и неравномерной по координатам r и z сетке, сгущающейся у свободной поверхности, у фронтов плавления и кристаллизации, а также на середине высоты мостика. Для генерации сетки используется следующее преобразование координат:

r _P r

z _ ^

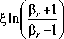
- 1

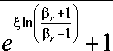
(1 + 4 n )ln S z +

L p _z + 1 + (1 -p z )e       ^e z ^{- 1}

4                   (1 + 4 n )ln e z + 1           ■

1 + e        ^e z ^{- 1}

(4 n- 3)ln ^e z ^{1 1}

L 3 -P z + ( P z + 3)e       ^e z ^{- 1}

n< 0,5,

4              (4 n- 3)ln &+

1 + e         ^e z ^{- 1}

n> 0,5,

где £ , n — новые координаты, изменяющиеся на отрезке [0,1]; P _r и P _z — параметры, позволяющие управлять степенью сгущения по каждой из координат. При P _{r z} ^ да сетка переходит в равномерную.

Частные производные в цилиндрической и преобразованной системах координат связываются формулами:

— _ RF — , d r      5^

— _ ZF — , d z     dn

— _ RS1— + RS 2 —, ²

d r

— _ ZS1 — + ZS 2 —.

d z ²       dn dn

Здесь RF1 _ 1

RS1 _ 1

S r ^ ²

S^J '

RS 2 _-

d ²r

5^ 2

[I J , k ^d ^J

ZF1 = 1

(#/ (SnJ

ZS 2 =

Az. ML dq2/ (dn J

4. Дискретизация по времени и численный метод

Для решения системы (5)–(10) применяется метод дробных шагов по времени. Компоненты скорости и давление вычисляются по следующей схеме. На каждом подшаге сначала по уравнениям движения для компонент с использованием поля давления с предыдущего подшага (или с предыдущего шага на первом подшаге) вычисляется промежуточное приближение для поля скорости, не являющееся бездивергентным; затем из условия соленоидальности поля скорости находится поправка для давления, с использованием которой получаются окончательные поля скорости и давления (см. например [9], где описан аналогичный подход в случае явной схемы дискретизации по времени).

Рассмотрим расчетную схему более подробно. Итак, на первом для вычисления промежуточного приближения и исправленных компонент а также поправки к давлению и нового давления имеем следующие формулы:

подшаге скорости,

Vm -

At

n m     nn    1    n    n m \ vm ) mpP      m. \ vm ) mr \ vm ) mz \m / ,

v m - v m A tG „. d ( v m ) = o, p^X = p n + q¹;

на втором подшаге:

^^ = - H m ( v m ) - GmP' + A m . ( Vm, ) + A mr (£ ) + Az ( V m ) , v m - v m = -A* 3 . q 2 , d ( v m ) = o, p = p^{1 +} q ²;

на третьем подшаге:

3 b

Vm Vm _ ТТ b^.bA f „2       L b \ , д ( b \ , д  M3\

--At-- = -Hm (Vm ) - Gmp + Am. (Vm ) + Amr (Vm ) + Amz (Vm) vn+1 - v3 = -MG <73 , m mm

d (v,m+1 )=o,

p"+ = p2 + q3.

Здесь операторы H_m ( v_m ) содержат разностное представление нелинейных

членов и

низших вязких членов; операторы A_m . , A_mr , A_mz и G_m представляют вязкие члены второго порядка и градиентные члены соответственно; D — оператор дивергенции; q ¹ , q ² , q ³ — поправки к давлению.

Для получения поправок q1 , q2 , q3 на каждом подшаге необходимо решить уравнение Пуассона

DG ( q l )=^ D ( v m ) - Q.

С этой целью воспользуемся дискретным преобразованием Фурье (FFT) по азимутальной координате ф :

■V

2 n i .

jn

, ^NФ     ,

1 ^N ф - ¹ q' ,j,k   _v X ^q^ ,n e

N ф n = 0

где i , j , k — индексы, нумерующие точку сетки в направлениях r , ф , z соответственно, К _ф — число узлов в азимутальном направлении, i — мнимая единица.

Подстановка (15) в (14) приводит к уравнению

(1 5 5 д д k )

1 -

ˆ qi’k-n     ^t Di-k-n ,

--r— +--+ — v r dr dr dz dz r y где kn =( cos (4nn / Nф)-1)/(2h<2); DDikn — Фурье-компонента дивергенции промежуточного поля скорости; hф = 2п / Nф .

Все пространственные производные аппроксимируются центральными или односторонними (в узлах на границах области) разностями второго порядка точности. Граничные условия для промежуточного поля скорости получаются путем проектирования соответствующих компонент уравнения Навье–Стокса на нормаль к поверхности. На оси симметрии используются уравнения движения, записанные в декартовой системе координат и аппроксимированные конечными разностями в ячейках, содержащих узел на оси и четыре ближайших к оси узла сетки цилиндрической системы координат, лежащих на декартовых осях. Преобразование компонент векторов производится в соответствии с формулами перехода между декартовой и цилиндрической системами координат.

Каждая из трех компонент уравнений (11)–(13) в разностной форме представляет собой систему алгебраических линейных уравнений с трехдиагональной матрицей, решаемую методом прогонки. Уравнение (16) приводит к системе линейных уравнений с ленточной матрицей, решаемой при помощи стандартных подпрограмм из пакета LINPACK. По сравнению с применявшимися в предыдущих работах итерационными методами, прямой метод решения уравнения Пуассона позволяет значительно сократить затраты процессорного времени. Наряду с однопотоковым разработан параллельный вариант программного кода; с его использованием вычисления ведутся на высокопроизводительных многопроцессорных компьютерных системах.

Для температуры и концентрации расчетная схема аналогична, но более проста ввиду отсутствия в соответствующих уравнениях градиентных слагаемых и необходимости вводить промежуточные поля.

• 5.    Численные результаты

  Вычисления проведены для фиксированных значениий параметров: Sc = 22,5; Pr = 0,00771; k₀ = 4,2 (для кремния с примесью фосфора); A h = 0,5; Bi = 2,0; L = 2. Безразмерная скорость протяжки V_g менялась от 0, 00412 до 0,1 ; тепловое и концентрационное числа Марангони — в пределах 0 <  Ma T <  30 и 0 <  Ma C <  100000. Наличие значительных градиентов (особенно в поле концентрации) требует использования достаточно мелкой сетки, но при этом необходимость получения результатов за приемлемое время служит ограничителем. Стационарные решения для случая V g = 0,1, Ma T = 10, Ma C = 0 на сетках размером 66 х 32 х 131, 44 х 24 х 89 и 33 х 20 х 65 узлов по осям r , ф , z , соответственно, дают значения максимальной величины вертикальной компоненты скорости 0,3435196051, 0,3441675067 и 0,3445117676. Сопоставление результатов показывает, что второе значение служит приемлемым компромиссом. В итоге сетка 44 х 24 х 89 была использована для проведения основной серии вычислений.

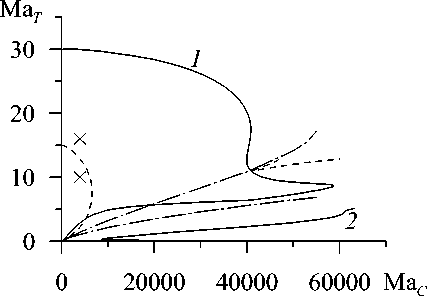
На рисунке 2 приведены фрагменты карт линейной устойчивости стационарного осесимметричного течения в жидком мостике относительно малых трехмерных возмущений. Карты получены в работе [8].

Рисунок 2, а соответствует скорости протяжки V g = 0,1. Между штрихпунктирными линиями находится область бистабильности, выше — область доминирования термокапиллярного механизма, ниже — концентрационно-капиллярного. Стационарный режим, в формировании которого доминирующую роль играет термокапиллярный механизм, устойчив относительно возмущений с волновым числом к = 2 внутри области, ограниченной штриховой линией, и неустойчив по отношению к таким возмущениям за пределами этой области. Сплошная линия 1 является границей устойчивости относительно возмущений с к = 1; область устойчивости находится внутри. Стационарный режим, в формировании которого главную роль играет концентрационная конвекция, теряет устойчивость относительно возмущений с к = 1 правее сплошной кривой 2 .

Карта устойчивости для V g = 0,00412 имеет аналогичный вид. На рисунке 2, б показан небольшой фрагмент этой карты в области малых значений Ma _T и положительных значений Ma _C . В выбранном масштабе граница смены преобладающего механизма круто уходит вверх у оси ординат (кривая 1 ) и видна практически только зона одновихревого концентрационного течения. Оно устойчиво слева и теряет устойчивость справа от сплошной линии, соответствующей возмущениям с к = 1 (кривая 2).

Точки на плоскости Ma C - Ma T , для которых проводились трехмерные расчеты, отмечены на рисунке 2 крестиками. Они относятся к значениям параметров за пределами области сосуществования режимов термокапиллярного и концентрационнокапиллярного происхождения.

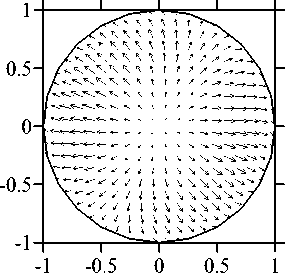
На рисунках 3-5 представлены результаты расчетов при V g = 0,1, Ma C = 4000 и двух значениях теплового числа Марангони: Ma T = 10 и Ma T = 16. В обоих случаях в качестве начального было взято состояние движения расплава вдоль оси со скоростью протяжки как твердого тела. При этих значениях параметров, согласно результатам решения стационарной осесимметричной задачи, доминирующим механизмом, индуцирующим стационарное движение, является термокапиллярный, который приводит к установлению двух противоположно направленных тороидальных вихрей в верхней и

MaT 0,3

0,2

0,1

а

Рис. 2. Фрагменты карт устойчивости стационарного осесимметричного течения для V g = 0,1 (а) и V g = 0,00412 (б) и различных значениях волнового числа: к = 0 (штрихпунктирные линии); к = 1 (сплошные); к = 2 (штриховые); крестиками указаны точки в пространстве параметров, для которых проведено трехмерное моделирование

0   200000 400000 600000 800000 MaC

б

а

б

-1    -0.5     0     0.5     1

в

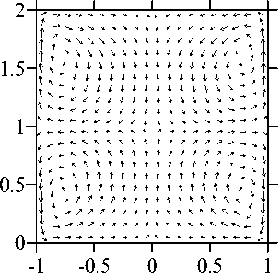
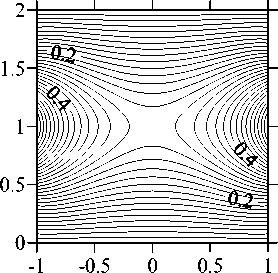
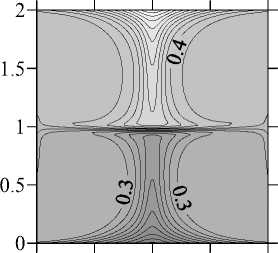
Рис. 3. Структура течения (а), изолинии температуры (б) и изолинии концентрации (в) в плоскости

Ф = 0 ... 180 ° при V g = 0,1, Ma C = 4000 и Ma T = 10

нижней частях жидкого мостика. Согласно данным линейного анализа устойчивости, проведенного в [8], точка Ma T = 10 находится в области устойчивости осесимметричного стационарного решения. Трехмерные численные расчеты подтверждают этот вывод: они также приводят к установлению осесимметричного стационарного режима (Рис. 3). Следует заметить, что в силу малости числа Прандтля распределение температуры имеет практически такой же вид при всех других рассмотренных значениях параметров и потому на последующих рисунках не приводится.

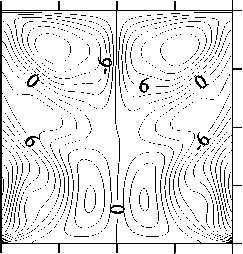
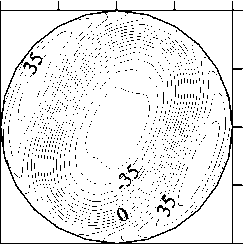
На рисунках 4 и 5 приведены поля скорости и концентрации, полученные в трехмерных численных расчетах при V g = 0,1, Ma C = 4000, Ma T = 16 (безразмерное время t = 21,2). Согласно данным линейного анализа устойчивости точка Ma T = 16 находится выше границы неустойчивости осесимметричного стационарного решения по отношению к возмущениям с азимутальным волновым числом равным 2 (см. Рис. 2, а). Как видно из рисунков 3 и 4, трехмерные численные расчеты подтверждают

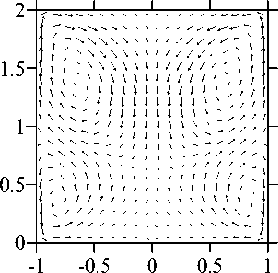
а

1.5

0.5

-1    -0.5     0     0.5     1

б

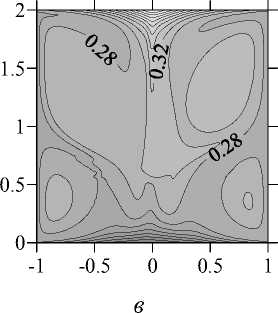
Рис. 4. Структура течения (а), изолинии азимутальной компоненты скорости (б) и изолинии концентрации

(в) в плоскости ф = 0... 180 ° при V g = 0,1, Ma C = 4000 и Ma T = 16

0.5

-0.5

-1

0.5

-0.5

-1

-1    -0.5     0     0.5     1

-1    -0.5     0     0.5     1

б

а

в

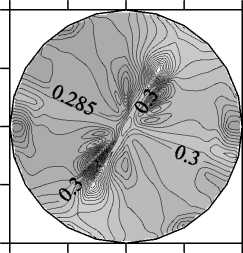
Рис. 5. Структура течения (а), изолинии z-компоненты скорости (б) и изолинии концентрации (в) в плоскости z = 1 при V g = 0,1, Ma C = 4000 и Ma T = 16

этот результат: на фоне вихрей термокапиллярного происхождения возникает неосесимметричное движение расплава, к тому же значительно нарушающее симметрию между верхней и нижней частями мостика, причем неустойчивость развивается по отношению к возмущениям с к = 2.

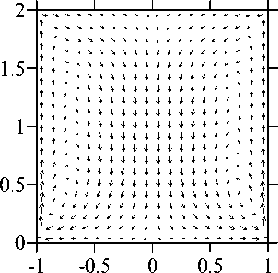
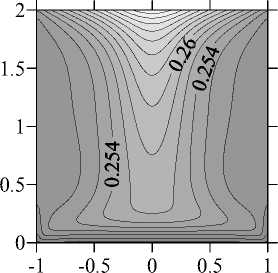
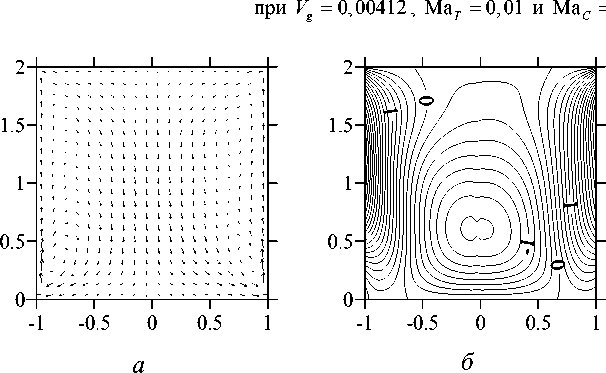
На рисунках 6-8 приведены результаты численных расчетов при V g = 0,00412 , Ma T = 0,01 и двух значениях концентрационного числа Марангони: Ma C = 300000 и Ma C = 700000 (безразмерное время t = 14,1). В качестве начального состояния бралось осесимметричное стационарное решение. В обоих случаях доминирующим механизмом, индуцирующим стационарное осесимметричное движение, является концентрационнокапиллярный механизм, приводящий к тому, что большую часть объема мостика занимает один тороидальный вихрь. Точка Ma C = 300000, в соответствии с данными линейного анализа устойчивости, располагается в области устойчивости осесимметричного стационарного решения. Трехмерные численные расчеты подтверждают этот вывод (см. Рис. 6). Точка Ma C = 700000 располагается в области неустойчивости стационарного осесимметричного решения по отношению к возмущениям с к = 1. Как видно из рисунков 7 и 8, трехмерные численные расчеты подтверждают и этот вывод. Таким образом, результаты проведенных трехмерных расчетов находятся в соответствии с данными линейной теории устойчивости.

а

б

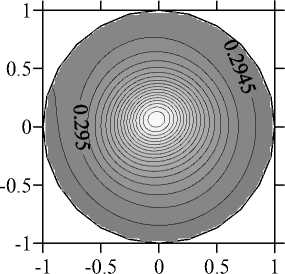
Рис. 6. Структура течения (а) и изолинии концентрации (б) в плоскости ф = 0... 180 °

в

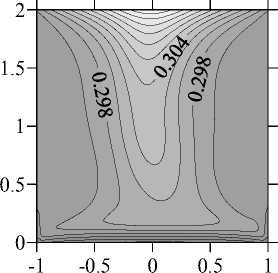
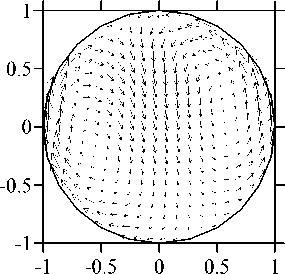
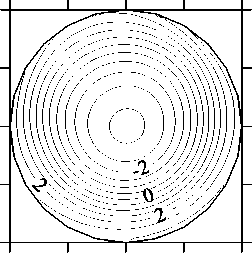
Рис. 7. Структура течения (а), изолинии азимутальной компоненты скорости (б) и изолинии концентрации (в) в плоскости ф = 0... 180 ° при V g = 0,00412, Ma T = 0,01 и Ma C = 700000

0.5

-0.5

-1

-1    -0.5     0     0.5     1

а

б

в

Рис. 8. Структура течения (а), изолинии z-компоненты скорости (б) и изолинии концентрации (в) в плоскости z = 1 при V g = 0,00412, Ma T = 0,01 и Ma C = 700000

• 6.    Заключение

Разработан алгоритм численного моделирования трехмерных нестационарных режимов термо- и концентрационно-капиллярной конвекции в цилиндрической жидкой зоне, основанный на решении нестационарных уравнений движения в естественных переменных методом конечных разностей в сочетании с методом дробных шагов по времени. Уравнение Пуассона для давления численно решается с применением дискретного преобразования Фурье в азимутальном направлении и использованием прямого метода решения результирующих двумерных уравнений Пуассона для Фурье-компонент поля давления с помощью подпрограмм из пакета LAPACK.

Проведена серия расчетов для значений определяющих параметров, соответствующих различным осесимметричным стационарным режимам и различным сценариям развития трехмерного движения. Подтверждены полученные ранее результаты анализа линейной устойчивости стационарного осесимметричного течения в жидкой зоне. Получены данные о временной эволюции интегральных характеристик течения и полей скорости, давления, температуры и концентрации. Трехмерное нестационарное моделирование с учетом обоих механизмов генерации движения выполнено впервые.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ и Федерального агентства по Образованию (программа «Развитие научного потенциала высшей школы»), CRDF (программа «Фундаментальные исследования и высшее образование») и Программы Президиума РАН «Интеллектуальные информационные технологии, математическое моделирование, системный анализ и автоматизация» (проект «Вычислительные технологии в задачах механики сплошных сред»).