Численное моделирование трехмерных турбулентных течений на основе математической модели волновых процессов

В прибрежных системах велика роль вертикального турбулентного обмена. В ряде случаев он определяет транспорт биогенных веществ, а также от него зависит насыщенность водной среды кислородом и, следовательно, возникновение заморных явлений (гибель обитателей от удушья) при отсутствии турбулентного перемешивания в водной толще. Задание коэффициента вертикального турбулентного обмена в виде константы приводит к искаженной картине распределения скоростей водной среды, а также концентраций биогенных веществ и кислорода по вертикальному направлению, кроме того, не обеспечивает требуемую точность расчета 3D течений. Последнее подтверждается сравнением результатов численного моделирования и непосредственно измеренного 3D вектора скорости водной среды при помощи оборудования типа ADCP (Acoustic Doppler Current Profiler).

Трехмерный характер течения, стохастическая природа и широкий пространственно-временной спектр турбулентности делает предсказательное моделирование характеристик сложных турбулентных течений сложной и трудоемкой задачей [1]. Однако расчет вертикальной структуры течения необходим для решения ряда прикладных проблем, в первую очередь антропогенного загрязнения акваторий, а также оценки надежности гидротехнических сооружений (защитных конструкций, нефтяных платформ, волнопреобразователей и других устройств), установленных в районах шельфовой зоны и в мелководных морях при наличии приливов и штормовых нагонов [2, 3].

Применяемые модели гидродинамических процессов можно разбить на два класса: двумерные линейные и базирующиеся на уравнениях мелкой воды трехмерные нелинейные модели. Наиболее известны: двумерная модель, созданная в Государственном океанографическом институте имени Н.Н. Зубова (Москва); трехмерная модель, построенная Гидрометцентром России; трехмерная модель INMOM, разработанная в Институте вычислительной математики РАН; модели, используемые в Морском гидрофизическом институте РАН (модифицированный вариант модели POM и модель ADCIRC, функционирующая в связке с волновой моделью SWAN); модели, реализуемые в ЮНЦ РАН (мультикомпартментальная балансовая модель и двухслойная модель гидродинамики водоемов [4‒9]).

Анализ существующих моделей гидродинамических процессов в прибрежной зоне мелководных водоемов показывает, что подавляющее большинство подходов к их построению основывается на приближении мелкой воды, или, в лучшем случае, на гидростатическом приближении, которое не учитывает турбулентный тепломассообмен по вертикальному направлению. Но имеющиеся опытные данные свидетельствуют о существенном влиянии этих процессов на гидрофизику береговой зоны, дислокацию солей и газовый режим. Поэтому построение, изучение и применение пространственнотрехмерных моделей гидродинамики, предусматривающих механизмы турбулентного обмена по вертикальной координате, представляется актуальной научной и важной прикладной проблемой.

Статья посвящена разработке и исследованию пространственно-неоднородной трехмерной модели волновой гидродинамики с усовершенствованной параметризацией коэффициента вертикального турбулентного обмена. Разработанные алгоритмы решения модельных задач гидрофизики и их численная реализация в виде проблемно-ориентированного программного комплекса имеют широкое практическое применение для исследования волновых процессов прибрежных систем, а также для расчета полей скоростей, давления водной среды и функции возвышения уровня при наличии поверхностных волн и турбулентного перемешивания.

2.    Пространственно-неоднородная трехмерная математическая модель волновой гидродинамики мелководного водоема

Пространственно-неоднородная трехмерная математическая модель волновой гидродинамики мелководного водоема включает (запись в декартовых координатах x , y , z ):

‒ уравнения движения (Навье‒Стокса)

u ,' + uu ‘ + vu y + wu ‘=-- P x + ( ц u ' ) x + ( ц u y ) y + ( ^v u ' ) z , v + uv ‘ + vv У + ^wv‘=-p p y + ( ц v ‘ ) x + ( ц v y ) _y + ( ^v v Z ) z , 1 ‘           ..'         .x' ..'

w _t+ uw , + vW y + ww = — P z + ( ц W x ) _x + ( ц W y ) _y + ( v W z ) _z + g ;

‒ уравнение неразрывности

P t +⁽P u ) x +⁽P v ) y +⁽P ^W ) z = ⁰ .

В уравнениях (1), (2) приняты обозначения: u , v , w — компоненты скорости водного потока мелководного водоема; p — плотность водной среды; p — гидродинамическое давление; g — ускорение свободного падения; ц , v — коэффициенты турбулентного обмена в горизонтальном и вертикальном направлениях; штрих и индекс обозначают частную производную по соответствующей декартовой координате. На рисунке 1 представлена батиметрия водного тела.

Пусть т = р a Cd s |w|w — вектор тангенциального напряжения для свободной поверхности, где Cd s — безразмерный коэффициент поверхностного сопротивления, который зависит от скорости ветра ( Cd s = 0,0026), w — вектор скорости ветра относительно воды, р a — плотность атмосферы.

Для дна зададим вектор тангенциального напряжения с учетом движения воды следующим образом: т = р Cd b |V|V , Cd b = gk ² / h ¹³ , где k — групповой коэффициент шероховатости в формуле Мэннинга,

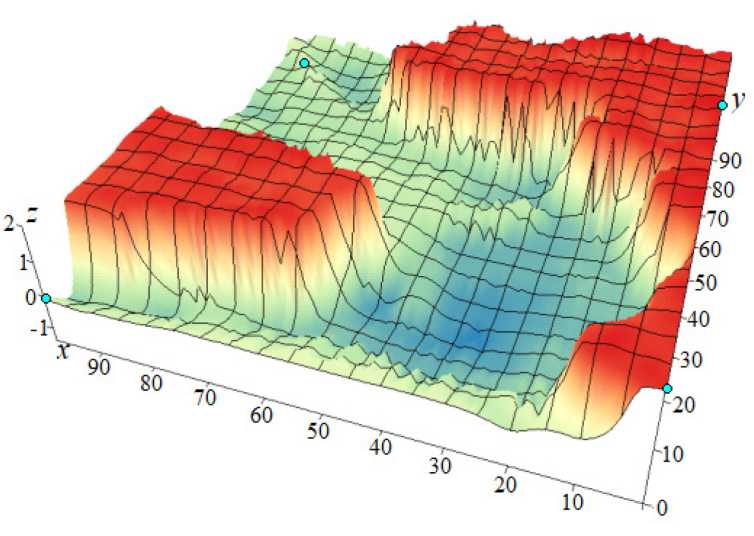
Рис. 1. Геометрия расчетной области (уровень невозмущенной жидкости соответствует z = 0 )

рассматриваемый в диапазоне 0,025–0,200 (здесь к = 0,04), h = H + п — глубина акватории, [м], при этом H — глубина до невозмущенной поверхности, п — высота свободной поверхности относительно геоида (уровня моря).

Будем использовать аппроксимацию, позволяющую строить неоднородный по глубине коэффициент вертикального турбулентного обмена на основании измеренных пульсаций скоростей водного потока:

д и

^V   C s ^Л 2 2 ^д z

+

д v д z

Здесь: C_s — безразмерная эмпирическая

константа, определяемая на основе расчета процесса затухания однородной изотропной турбулентности;

Л — характерный масштаб сетки; и, v — осредненные по времени пульсации компонент скорости водного потока в горизонтальном направлении.

3.    Дискретная математическая модель задачи гидродинамики

Расчетную область впишем в параллелепипед. Для построения дискретной математической модели поставленной задачи гидродинамики и ее численной реализации введем равномерную сетку:

w_h = { t n = n т, x i = ih x , y j = jh y ,   z_k = kh z ;   n = 0, N_t , i = 0, N x , j = 0, N_y , к = 0, N_z ;

Ntт = T, Nxhx = lx, Nyhy = ly, Nzhz = lz} , где т — шаг по времени, hx, hy , hz — шаги по пространству, Nt — количество временных слоев, T — верхняя граница по временной координате, Nx , Ny , Nz — количество узлов по пространственным координатам, lx , ly , lz — длины ребер элементарного параллелепипеда в направлении осей Ox , Oy и Oz соответственно.

Для решения задачи гидродинамики воспользуемся методом поправки к давлению. Вариант метода в случае переменной плотности принимает вид [10]:

U - и

--+ uux + vuy + wuz =(цux)x + (циy) +(vuz)z , v - v

--+ uv ‘ + vv ‘, + wv.

т

x

y

'                         '                        '

’z = ( ^ ^Vx ) x ⁺ ( p 4 y ) y ^{+ (v V} ) z -

wv - w   -r              ( -1 V ( -i\' ( -1\’

--+ uwx + vw_y + ww_z = ( Ц w_x ) x + ( ц w_y ) + ( v w_z ) z + g ,

p x ⁺ p yy ⁺ p z =

P-P , (Pu_)'x , (Pv)'y ,(pw)\ 2  +      ++ т т т т

/\      ^/           1                   /у ^,           1                     /у       w1

u - и     1        v -1^     1         w - vw1

----- =-- Р ' ,    ----- =-- P y ,    ------ =-- P z .

т P т P          т P

Здесь: u , v , w — компоненты вектора скорости V = { u , v , w } ; {£ 2, v, iw } , { u, i ⁵, wv } — компоненты полей скорости на «новом» и промежуточном временных слоях соответственно; u = ( й + и )/ 2; P и p — распределение плотности водной среды на новом и предыдущем временных слоях.

4.    Фильтрация данных, полученных с помощью ADCP-зонда в ходе экспедиции

Интерес к турбулентности в мелководных водоемах типа Азовского моря вызван тем, что в местах ее существования происходит интенсивная передача количества движения и тепла, распространение пассивных примесей, перенос взвешенных частиц. Эти процессы существенно влияют на формирование и пространственную структуру физических, химических и биологических полей водоемов и их временные изменения. Обработка собранного эмпирического материала ведется для изучения внутренней структуры зафиксированных возмущений мелкомасштабной турбулентности, определения скорости диссипации энергии возмущений.

Для оценок характеристик турбулентности на основе прямых методов существует проблема, связанная с необходимостью владения большими объемами данных, которые могут дать длительные и дорогостоящие экспедиционные измерения. В обсуждаемом исследовании применим натурные данные, полученные в ходе экспедиции в Центрально-Восточной части Азовского моря и в Таганрогском заливе на научноисследовательском судне «Денеб» Южного научного центра РАН. Для измерения трехмерного вектора скорости движения водной среды использовался гидрофизический ADCP-зонд Workhorse Sentinel 600. Исследования проводились на 17 станциях. Измерения профиля течения водного потока проводились по вертикали и начинались от ближней зоны чувствительности ADCP-зонда до дна. Результаты замеров фиксировались с интервалом времени 1 с через каждые 10 см по глубине. Сохранение данных происходило по трем направлениям течения водного потока. Таким образом, при заданном разрешении по вертикали и шаге по времени для временного интервала 20–30 мин производилось более 3 000 000 исходных измерений в каждой заданной точке на каждой из 17 станций, то есть было задействовано более 150 000 точек.

Экспедиции преследовали цель — накопить информацию о состоянии и изменениях гидрофизических и гидрохимических параметров. В рейсах фиксировались параметры: пульсации компонент скорости течения; погрешность измерения; глубина водоема в месте измерения; направление и скорость ветра. В мелководных водоемах плотностная стратификация отсутствует, процессы в вертикальном направлении носят существенно нелинейный характер, поэтому прибегали к нестандартному методу оценки коэффициента вертикальной турбулентной вязкости, а именно по градиенту средней скорости потока.

Погрешность измерения пульсаций вертикальной компоненты скорости является одной из трудно устранимых проблем, поскольку она связана со многими явлениями, происходящими в водоеме в момент измерения, такими как девиация (отклонение от установленного пути следования) судна, изменения глубины водоема и его устойчивости, силы и направления ветра, волнения, колебания свободной поверхности. Степень влияния качки учитывается посредством введения редукционных коэффициентов, зависящих от длины волны, и, следовательно, от частоты волнения. Ими служат амплитудно-частотные характеристики линейных низкочастотных фильтров.

Рассмотрим применение различных фильтров для обработки мгновенных скоростей водного потока, измеренных в полевых условиях.

Мелкомасштабное движение исключим из уравнений Навье‒Стокса при помощи операции фильтрации и используем для представления турбулентности подсеточные модели. Результаты расчетов методом крупных вихрей (LES) зависят от ширины фильтра, которая входит в оператор фильтрации и обычно связывается с размером шага разностной сетки. Уменьшение ширины фильтра позволяет воспроизвести более широкий частотный диапазон флуктуаций решения, увеличение способствует сглаживанию решения.

Введем обобщенный фильтр, дающий формальное определение операции осреднения и позволяющий исключить масштабы, меньшие некоторой наперед заданной величины А. В качестве последней возьмем ширину фильтра. Вихри, размер которых меньше, чем ширина фильтра, не разрешаются [11]. Обобщенный фильтр сформулируем следующим образом: f (x, t) = | f (^, t)g (x,£, А)d^ . В том случае, когда функция D g (x, ^) зависит только от разности x - ^, операции дифференцирования и фильтрации коммутируемы. Тогда обобщенный фильтр выглядит как интеграл свертки: f (x, t) = | f (^, t) g (x — £, А) d§ = f (x, t )• g (x, А).

D

Предполагаем, что фильтрующая функция g (x), называемая также ядром фильтра, является четной и бесконечно дифференцируемой в ограниченной области D , имеет компактный носитель и удовлетворяет условию нормирования: g (x) = g (-x), |g (£, А) d£ = 1. В предельном случае выполняются соотношения: D lim| f (£,t)g(x-£, А)d^ = f (x,t), limg(x, А) = 5(x). Интегрирование проводится по всей области D течения D . Фильтрующая функция определяет структуру и размер мелкомасштабных турбулентных вихрей, разрешаемых системой осредненных уравнений. Согласно теореме Бореля о свертке, преобразование    Фурье свертки равняется произведению преобразований    Фурье:

F [ ^{f (} x , t ) • g ⁽ x ^ = F [ f ( x , t ) ] F [ g ( x ) ] . Преобразованием Фурье функции f ( x ) , абсолютная величина | f ( x )| которой интегрируема на интервале -го <  x <+го , называется функция c ( k ) = F [ f ( x ) ] , где +го                                                                                                          +го

c ( ^k ) = | f ( x ) exp ( - i kx ) d x . Формула обращения имеет вид: f ( x ) = | c ( k ) exp ( i kx ) d k .

-го

-го

Приведем выражения фильтров, используемых в расчетах:

- коробочный фильтр g ( x - ^ ) =

1 A 3, | х , -фА xj2, 0, x ^-L J >  ^A x /2;

- фильтр Гаусса g ( x - ^ ) = ( б/ ( nA ² ) ) exp [-6 |x -^| 2 /a ² ];

;

1 sin25              x . -L

^— фильтр Фурье g ( x ^- ^ ) = -тП ——, где ^{5 п} A       5.                 A

.

Для представления наименьших разрешимых масштабов необходимо, чтобы ширина фильтра не превосходила шага разностной сетки. Обычно различие между этими величинами игнорируется и ширина фильтра полагается равной А = V 13 = (Ax Aу Az)13, где V — объем ячейки разностной сетки; Ax, Aу, Az — шаги сетки в координатных направлениях x , y и z соответственно. Поскольку ширина фильтра зависит от разностной сетки, то фильтрующую функцию часто называют сеточным фильтром.

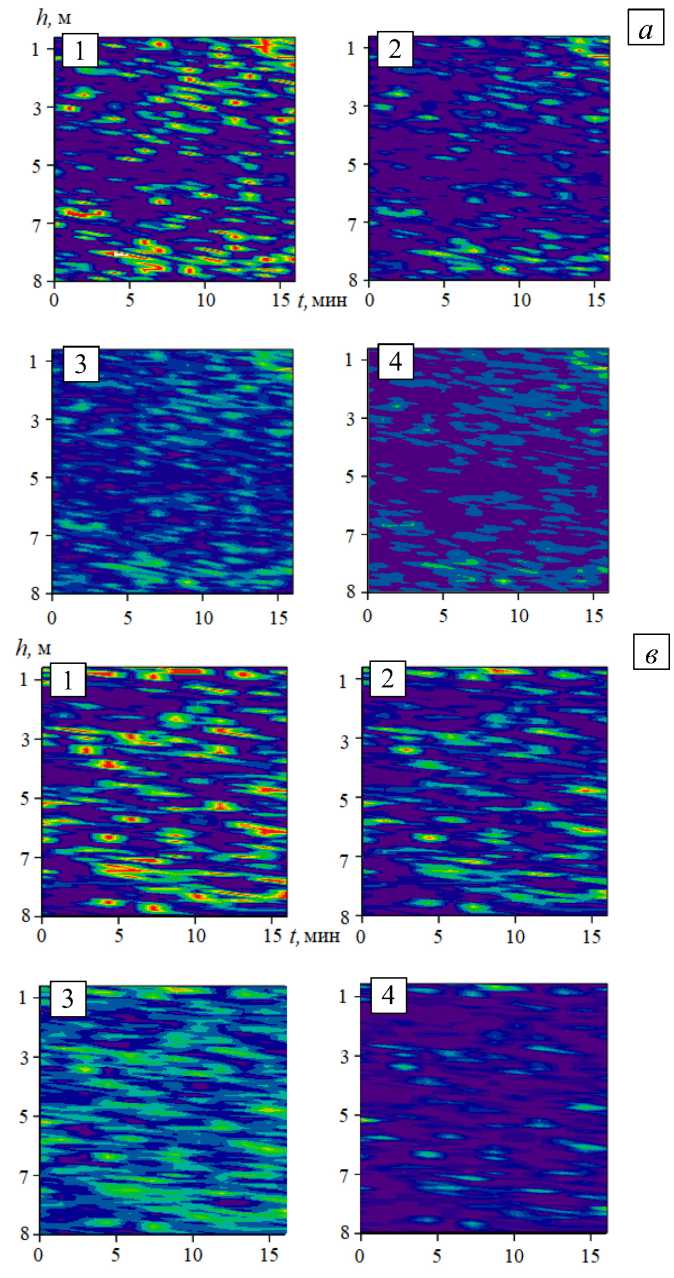
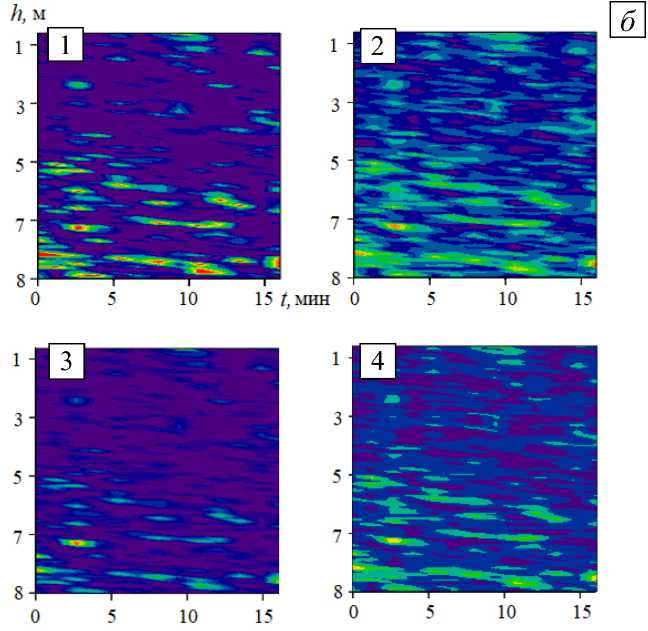
Рис. 2. Результаты фильтрации данных коробочным фильтром ( а ), фильтром Гаусса ( б ), фильтром Фурье ( в ); на фрагментах 1 исходные данные, на 2, 3, 4 – данные после соответствующей фильтрации при различной ширине фильтра: A 4 < A 3 < A 2

При расчете в пограничных слоях предлагается заменить Aу — шаг сетки в нормальном к границе направлении, величиной Aу и находить ширину фильтра из соотношения А = (Ax Ау Az)Z , причем Ау = Aу вблизи границы и Ау = Ау вдали от нее. Промежуточные значения шага получаются плавным переходом от одного предельного значения к другому. Величина Ау представляет собой среднее значение Ау в приграничной области, а величина Ау рассчитывается по формуле:

Ау=[(VАу )3 +(VАу )3 ]'

При фильтрации уравнений Навье–Стокса фильтрующую функцию выбираем такой, чтобы выполнялось условие: (g*, V)u = 0. Будем использовать коробочный фильтр, фильтр Гаусса и фильтр Фурье при трех вариантах их ширины: А4 < A3 < А2. В данных расчетах ширину фильтров зададим исходя из размерности решаемой задачи гидродинамики и соответствующей размерности расчетной сетки.

Рисунок 2 демонстрирует результат устранения зашумленности экспедиционных измерений на примере одной из составляющих вектора скорости водного потока, в двумерном случае. Цветом выделена скорость водного потока в мм/с в соответствии с приведенной цветовой шкалой.

5.    Декомпозиция рядов эмпирических данных, полученных с помощью ADCP

Задача декомпозиции временных рядов эмпирических данных принадлежит к классу обратных задач обработки и интерпретации экспериментальных данных. В основе выделения требуемой в настоящем исследовании регулярной волны лежит набор процедур сглаживания скользящей средней мгновенных пульсаций скорости водного потока, измеренных в ходе экспедиции. Обработка каждого ряда производится в три этапа: первоначальная, промежуточная и окончательная, и далее фиксируется скорректированный ряд, который используется в качестве входных данных для трехмерной модели гидродинамики.

Для оценки регулярного волнения необходимо сформировать модель тренда, а после ее исключения из скорректированного ряда получается промежуточная регулярная волна и ее «зашумленные» сезонные компоненты.

«Зашумленные» сезонные компоненты сглаживаются скользящей средней, в результате осредняются отдельные составляющие и исключается мелкомасштабное движение, то есть высокочастотные составляющие временного ряда. На этом этапе сезонные коэффициенты нормируются так, чтобы их произведение на каждом рассматриваемом периоде равнялось единице. После этого делением исходного ряда на оценку сезонного фактора и тренда устанавливается «зашумленная» скорректированная компонента.

На следующем этапе к сезонной компоненте применяется процедура сглаживания взвешенным скользящим средним Хендерсона. На финальном этапе компоненты «зашумленного» скорректированного ряда опять обрабатываются посредством сглаживания, и выделяется окончательная регулярная компонента. С ее помощью извлекается иррегулярная составляющая, которая необходима для статистической идентификации регулярной волны для Азовского моря.

В качестве циклических компонент выступали гармоники основного колебания, то есть гармоники регулярной волны Азовского моря. Стационарная волна формировалась как аддитивная смесь основного колебания и трех высших гармоник в интервале, которая затем искажалась так, чтобы максимальные значения на положительной и отрицательной полуволнах отличались. Таким способом осуществлялась «дегармонизация» сезонной волны с целью максимального приближения к реальным волновым компонентам.

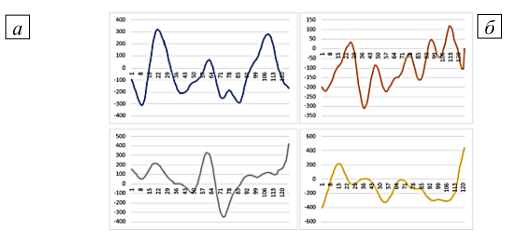
На рисунке 3 а представлены исходные данные с 4-х наблюдательных станций. На каждой станции произведено осреднение данных центрированным алгоритмом скользящей средней (Рис. 3 б ), в результате исключались низко- или высокочастотные колебания, затем осредненные данные подвергались процедуре фильтрации, что позволило снизить степень влияния мелкомасштабного движения на мгновенные скорости водного потока (Рис. 3 в ).

Шумовая компонента формировалась с помощью функции RAND пакета Microsoft Excel. Был выбран вариант с равномерной плотностью распределения случайных отсчетов и нулевым средним значением (нулевым первым моментом). Оценка дисперсии шумовой компоненты функцией STDEV пакета Excel составляла 10% от оценки дисперсии циклической компоненты, и таким образом фиксировалось отношение шум/циклическая компонента (отношение шум/сигнал). Изменением масштаба по оси ординат в два и три раза находились и фиксировались различные отношения шум/сигнал.

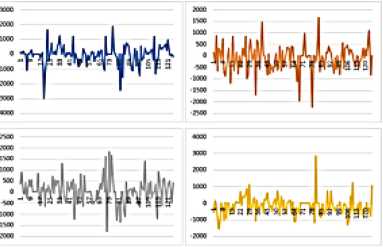
Минимизация корреляционных связей шумовой компоненты осуществлялась следующим способом: из реализаций выбиралась та, у которой пик автокорреляционной функции имел наименьшую ширину. Более строгая процедура «отбеливания» шумовой компоненты на конечном интервале времени осуществлялась на основе той же задачи выделения циклической компоненты с периодом, равным периоду регулярной волны, из реализации процедурой RAND случайного процесса с равномерной плотностью распределения (Рис. 4 а ).

Таким образом, после обработки данных, поступивших с зонда ADCP, выявлено, что характерная длина регулярной волны для Азовского моря составляет рана 15–25 м, характерная скорость — 0,1–0,2 м/с, максимальная скорость — 0,51–0,77 м/с (Рис. 4 б ). Данные, полученные в результате моделирования, согласуются с данными, представленными Единой государственной системой информации об обстановке в мировом океане (ЕСИМ).

В настоящей работе выполнен расчет коэффициентов турбулентного обмена для набора периодов турбулентных пульсаций скоростей. С использованием осредненных экспериментальных данных о пульсациях компонент скорости вычислен коэффициент вертикального турбулентного обмена на основании различных подходов к его параметризации.

а

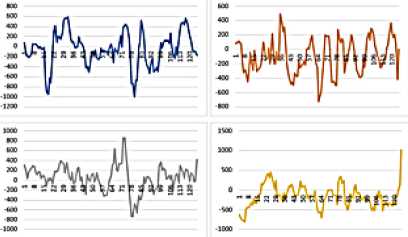
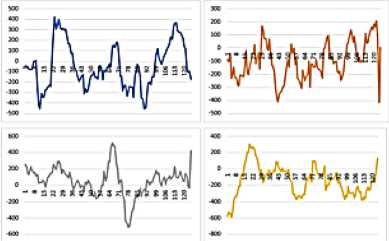
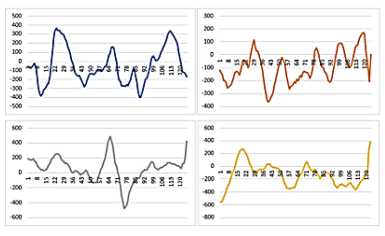
Рис. 4. Ряды данных с 4-х наблюдательных станций, полученные на основе осреднения фильтрации и устранения шумовой компоненты ( а ) и выделением циклической компоненты с периодом, равным периоду регулярной волны, из реализации случайного процесса с равномерной плотностью распределения процедурой RAND ( б ); размерность по вертикали [мм/с], по горизонтали [м]

Рис. 3. Ряды данных (мгновенные скорости водного потока) с 4-х наблюдательных станций: исходные данные ( а ); осредненные данные с зонда ADCP ( б ) и они же после фильтрации ( в ); размерность по вертикальной оси [мм/с], по горизонтальной [м]

6.    Параметризация коэффициента вертикального турбулентного обмена

Параметризация процесса турбулентного обмена в дискретных гидродинамических задачах, в первую очередь, для вертикального координатного направления выполняется на основе современных подсеточных моделей с учетом градиента плотности водной среды. Рассмотрены алгебраические подсеточные модели, в которых турбулентные потоки представляются в виде осредненных по пространству или времени произведений отклонений составляющих скорости течений и переносимой физической величины [1]. Выполнены вычислительные эксперименты по определению коэффициента турбулентного обмена по вертикали — v , с применением нескольких подходов:

- параметризация Белоцерковского v = ( C A z )

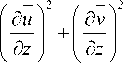
- параметризация Буссинеска v = ( 0,41 z ) ² 0,5

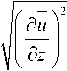
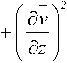
- параметризация Смагоринского v

0,5 ( C А ) ²

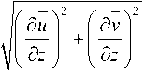
Здесь: u , v — осредненные по времени пульсации компонент скорости водного потока в горизонтальных направлениях; C — безразмерная эмпирическая константа; А — характерный шаг сетки. Использовались отфильтрованные распределения трехмерного вектора мгновенной скорости водного потока для глубин от 0,8 до 20 м и более, полученные при помощи ADCP WHS 600 WHS 1200 Sentinel.

Явление резких скачков величины коэффициента на всех графиках (см. Рис. 5), связано, с погрешностью измерений пульсаций вертикальной компоненты скорости, которая входит в расчетные формулы.

Погрешность измерений обусловливается многими явлениями, происходящими в водоеме в момент замера (девиация судна, колебания свободной поверхности воды, изменения глубины и устойчивости водных масс, ветер и волнение и другие).

Таким образом, на основе перечисленных подходов к параметрическому расчету коэффициента вертикального турбулентного обмена получены распределения, которые неоднородны по вертикали во всех точках замеров. Сравнительный анализ распределений показывает, что результаты параметризации на основе всех подходов близки как по порядку величины, а также по местоположению пиков на графиках.

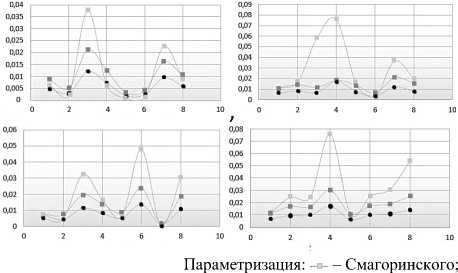
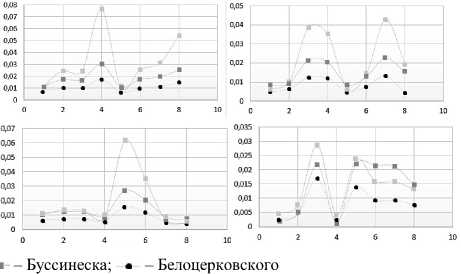
Рис. 5. Коэффициенты вертикального турбулентного обмена, рассчитанные на основе разных аппроксимаций для параметризации вертикального турбулентного перемешивания на 8-ми наблюдательных станциях (по вертикальной оси – значения коэффициентов в [м²/с], по горизонтальной – глубина в [м])

Для оценки качества параметризации необходим более глубокий анализ с применением методов математической статистики. С этой целью были рассчитаны средняя величина коэффициента вертикального турбулентного обмена, размах вариации, дисперсия, среднеквадратическое отклонение, коэффициент вариации, коэффициент осцилляции, коэффициент асимметрии, коэффициент эксцесса и проверена гипотеза о нормальности распределения. Таким образом, на основе статистического анализа, удалось выявить, что наименьшим среднеквадратичным отклонением обладают коэффициенты вертикального турбулентного обмена, найденные по формуле Смагоринского. При данной параметризации в большинстве случаев гипотеза о нормальности распределения выполняется.

7.    Моделирование влияния регулярных волн на турбулентный обмен по вертикали

Трехмерная модель позволяет проводить оценку влияния регулярных волн на турбулентный обмен по вертикали для мелководных акваторий. Созданный на ее основе авторский программный пакет адаптирован для моделирования гидродинамических волновых процессов и применим в широком спектре параметров для расчета полей скоростей и давлений водной среды, а также для оценки влияния регулярных волн на турбулентный обмен по вертикали.

По результатам проведенных численных экспериментов осуществлен анализ распределений коэффициентов вертикального турбулентного обмена, полученных с помощью параметризации Смагоринского, с учетом влияния регулярных волн и в их отсутствие. На рисунке 6 представлены профили коэффициента вертикального турбулентного обмена.

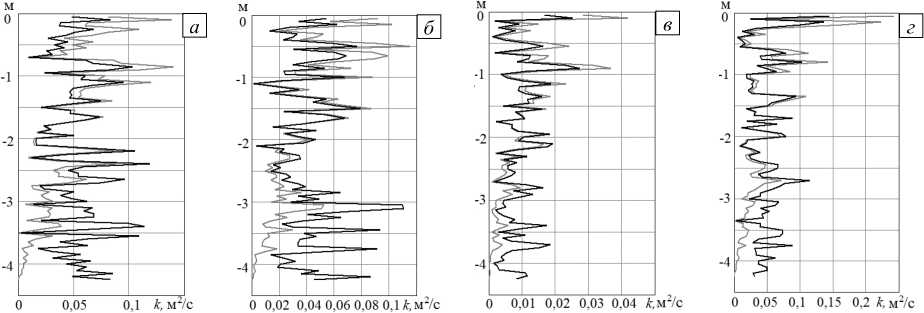
Рис. 6. Профили коэффициента вертикального турбулентного обмена для 4-х наблюдательных станциях на глубинах от 0 да 4 м (черная линия - без учета регулярных волн, серая - с учетом регулярных волн )

Подтверждено расслоение волнового потока на приповерхностный турбулентный слой, индуцированный волновым движением, и нижележащий слой с фоновой гидродинамической турбулентностью. Характерной особенностью влияния регулярных волн на турбулентный обмен по вертикали является увеличение коэффициента турбулентного обмена в приповерхностном слое и уменьшение в придонном слое [15].

Рисунок 6 свидетельствует, что турбулентность зарождается в верхней части потока, толщина приповерхностного турбулентного слоя линейно связана с высотой и длиной волны, толщина турбулизованного приповерхностного слоя по визуальным оценкам имеет порядок высоты волны. Видно четкое расслоение волнового потока на приповерхностный слой, и нижележащую область с относительно продолжительным временем их существования. В верхнем слое течение индуцируется волнами и направлено вправо, а ниже возникает компенсационный поток противоположного направления. Вертикальный размер слоя интенсивной турбулентности близок к трем четвертям высоты волны. Характеристики турбулентности верхнего слоя линейно связаны с величиной огибающей волновой компоненты вертикальной скорости частиц воды, что позволяет рассматривать турбулентность в верхнем слое как индуцированную волнами.

Продемонстрирован широкий диапазон изменчивости турбулентных пульсаций скорости (Рис. 7). Выявлено, что сила и интенсивность турбулентности изменяются синхронно с волновыми колебаниями, имеют отчетливо выраженную асимметрию генерации турбулентности по всей толще воды, в том числе и в приповерхностном слое, где волны усиливают флюктуации скорости течения. Поэтому под интенсивностью турбулентности следует понимать общий вклад в нее пульсаций скорости, поступающий как от мелкомасштабной турбулентности, так и от орбитальных движений, вызываемых гравитационными волнами.

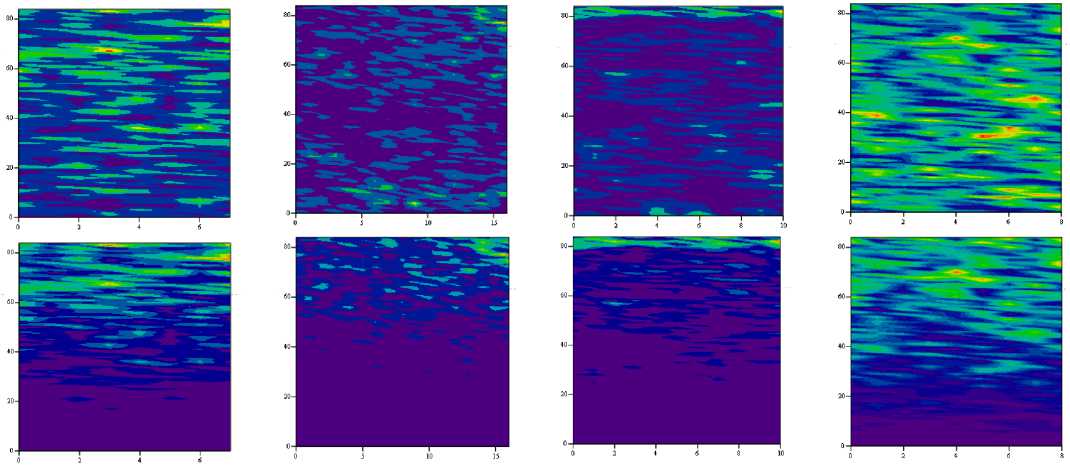
Рис. 7. Результаты моделирования вертикального турбулентного обмена: верхний ряд – без регулярных волн, нижний ряд – с учетом регулярных волн

8.    Описание программного комплекса

Трехмерная модель оценки влияния регулярных волн на турбулентный обмен по вертикали для мелководных акваторий положена в основу сконструированного программного комплекса, предназначенного для вычисления

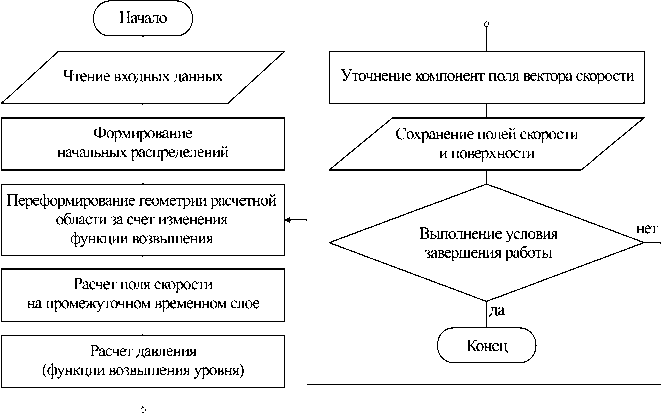
Рис. 8. Алгоритм вычислительного эксперимента

трехмерных полей скорости движения водной среды, с учетом неоднородного по глубине коэффициента вертикального турбулентного обмена и динамического перестроения геометрии расчетной области. Программный комплекс реализован на языке С++ [13, 14]. Выходными параметрами являются: шаги по пространственным координатам; погрешность решения сеточных уравнений; размерность расчетной сетки; принятый к рассмотрению временной интервал; интенсивность испарения; исходные распределения компонент вектора скорости движения водной среды и давления. Алгоритм вычислительного эксперимента представлен на рисунке 8.

9.    Численный эксперимент

Разработанный комплекс программ позволяет задавать сложную геометрию дна, вид и характеристики источника колебаний, направление ветра (Рис. 9). Для моделирования предлагается геометрия дна типа «узкое место» с глубинами, приближенными к геометрии дна Керченского пролива. Источник возмущений устанавливается на заданном расстоянии от береговой линии. Площадь моделирования имеет размеры 50x50 км и глубину 18 м.

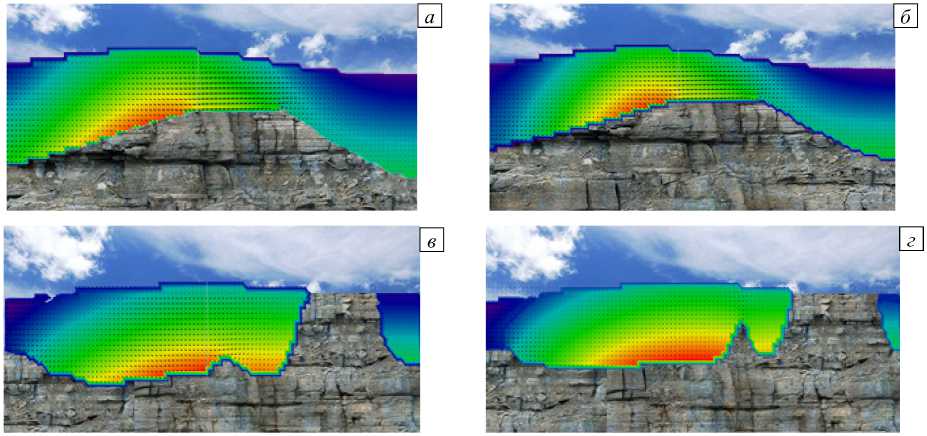
Рис. 9. Векторное поле скорости движения водной среды в различные моменты времени t , с: 5 ( а , в ) и 35 ( б , г ), и разных профилях дна

Разработанный программный комплекс использовался для численного построения прогноза движения водной среды. Результаты численных экспериментов по моделированию распространения волновых гидродинамических процессов на основе 3D модели движения водной среды, учитывающей неоднородность турбулентного перемешивания по вертикальному направлению, представлены на рисунке 10 в различные моменты времени. На рисунке хорошо видны изменения гидродинамического волнового процесса прибрежной зоны, формирование вихревых структур. Разработанный программный инструментарий позволяет задавать параметры источника колебаний, а также батиметрию водоема.

Для проверки адекватности созданной трехмерной модели результаты авторских расчетов были сопоставлены с известными авторам настоящего исследования численными и опытными данными. Отмечено хорошее согласие полученных результатов по основным этапам распространения и обрушения поверхностной волны.

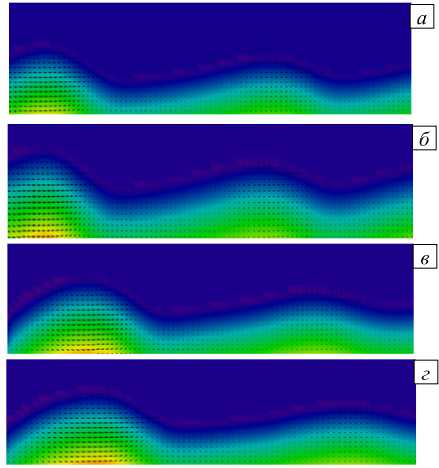
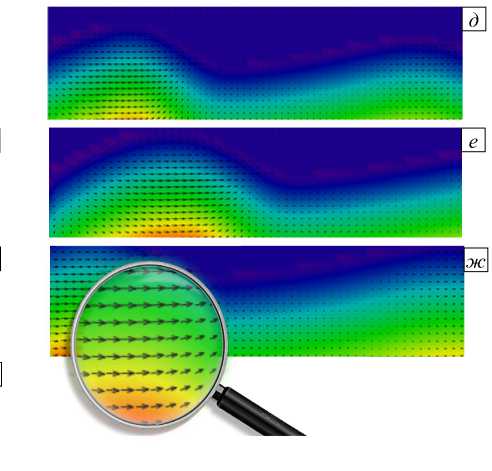
Рис. 10. Профили волн и векторные поля скорости в различные моменты времени t , с: 5 ( а ), 10 ( б ), 15 ( в ), 20 ( г ), 25 ( д ), 30 ( е ), 35 ( ж ); формирование вихревых структур ( д - ж )

10.    Заключение

Разработанный численный алгоритм и реализующий его комплекс программ может использоваться при исследовании гидрофизических процессов в прибрежных водных системах, а также для нахождения поля скоростей и давления водной среды, оценки их возможного негативного воздействия на береговую линию при наличии поверхностных волн. Программное обеспечение позволило обработать большой объем данных натурных наблюдений движения и параметров водной среды в акватории Азовского моря, который был получен в ходе экспедиционных исследований посредством применения гидрофизического зонда ADCP. Процедура фильтрации натурных данных позволила существенно снизить разброс данных и амплитуду колебаний, что в свою очередь позволило осреднить данные и наиболее адекватно оценить информацию. Выявлено, что результаты численного моделирования на основе обработанных эмпирических данных, осуществленного авторами, хорошо согласуются с данными, представленными Единой государственной системой информации об обстановке в мировом океане.

Рассмотрены возможности разных типов аппроксимации для параметризации вертикального турбулентного обмена. С помощью ADCP данных о пульсациях скорости для нескольких станций измерения гидрологических характеристик проведен анализ результатов параметризации коэффициента вертикального турбулентного обмена.

Созданный современный программный комплекс может быть адаптирован для моделирования гидродинамических волновых процессов в широком диапазоне параметров для расчета полей скоростей и давления водной среды, для оценки гидродинамического воздействия на берег при наличии поверхностных волн. Комплекс позволяет менять характеристики и расположение источника колебаний, учитывать форму зон и степень интенсивности осушения и затопления прибрежных участков. Он может использоваться для прогнозирования изменения процессов водной экологии в результате опасных явлений природного и техногенного характеров.

Вычислительные эксперименты, моделирующие распространения волновых гидродинамических процессов на основе 3D модели движения водной среды, учитывающей неоднородность турбулентного перемешивания по вертикальному направлению, дают возможность изучать влияние волн на передачу импульса в горизонтальных и вертикальных направлениях.

Исследование выполнено за счет гранта Российского научного фонда (проект № 22-71-00015),