Численное моделирование турбулентного диффузионного пламени на основе метода крупных вихрей

Математическое моделирование турбулентного горения определяется на сегодняшний день как одно из наиболее важных и одновременно сложных направлений вычислительной гидрогазодинамики [1]. Цель настоящей работы состоит в проведении численных исследований турбулентного диффузионного пламени на основе предлагаемой методики моделирования дозвуковых турбулентных течений сжимаемого реагирующего газа. В задачах, рассматривающих турбулентные реагирующие потоки, которые характеризуются наличием осцилляций течения, связанных с вихревыми структурами, необходимо учитывать влияние пульсаций параметров потока на скорость химических реакций и устойчивость процесса горения. В подобных случаях для решения требуется привлечение методов, позволяющих получать наиболее детальное описание характеристик турбулентного течения, таких как мгновенные значения скорости и температуры. Здесь для численного исследования турбулентных реагирующих потоков используется метод крупных вихрей (Large Eddy Simulation — LES), в практику которого привлекаются подсеточные модели как для описания мелкомасштабной турбулентности, так и протекания химических реакций. Для определения скорости реакции окисления в качестве основы принята модель «разрушения вихрей» (Eddy-Break-Up) с дальнейшим внесением предлагаемых кинетических модификаций.

2.    Основные уравнения

Течение сжимаемого реагирующего газа описывается системой уравнений Навье–Стокса, дополненной уравнениями энергии и массовых концентраций горючего и окислителя. Основой метода крупных вихрей является пространственная фильтрация исходных уравнений [2]. В настоящей работе фильтрация явным образом не проводится, а выполняется неявно при пространственной дискретизации исходной системы уравнений. С применением взвешивания по Фавру f = рf /'р система уравнений имеет вид др

— + д t

^( Р ^U j ) = 0, д x j

^д( р « / ) д t

д

⁺ a x; (^р j

^L + Af (n + n ) /u + ■ - 2 X ^k 11-1 д дx .   дx-         sgs   дx-   дx   3 j дxk      3 дx- j \                    j                        k / j

( i = 1,2,3),

^д (р h i)   д / _п

----  +--р и h = д t     дxj     J 7

^д u

д u i

д Р    д        ^и<Л:   J^j   Z.    ^Uk

^{+ Ц} -   ' --- "7⁵ij^T" ¹¹ i

дU,

Л

д t

дx

' j V

V

дx

j

д x ,

3 j ^j д x.

' k у

д

дx

Ц + ^Ц sgs

Pr Pr sgs

д /г дx,

^J 7

+ q chem ,

д ( р ё f ) д t

д /___\ д

+--- р и Cf =--- дx?'  J п  дxj

'j VV

Ц

Sc

^Ц sgs

Sc sgs 7

д ё

______J д x

- w ,

^д( р ^ёox ) д t

. д -

+--ри iCm дxjv J 00

)=-' д x j

' j VV

Ц

Sc

^Ц sgs

Sc sgs 7

д c ox дxj

- v w ,

где xi — декартовы координаты; и, — компоненты вектора скорости реагирующего газа; t — время; p — давление газа; р — плотность газа; h — энтальпия газа; ёf — массовая концентрация горючего; ёox — массовая концентрация окислителя; qchem — источниковый член, связанный с массовой скоростью химической реакции окисления qchem = дhwv, где дh — теплота реакции, vv — массовая скорость реакции; ц — динамическая вязкость газа; цsgs — подсеточная вихревая вязкость; тkk — изотропная часть тензора подсеточных напряжений, появляющихся в уравнениях в результате их фильтрации; 5jj

символ

Кронекера; v

стехиометрический коэффициент; Pr, Sc

числа Прандтля и Шмидта;

Pr _sgs , Sc _sgs — подсеточные числа Прандтля и Шмидта.

В модели Смагоринского, обобщенной для сжимаемых течений [3], подсеточная вихревая вязкость цsgs определяется как функция вида цsgs = рCS2A2 |S|, где CS — параметр Смагоринского; А — ширина фильтра; |S| = ^2SjSi

•v

S = 1 f^, ’ ^ij 2 д x j

д u i

______J дx,

— тензор скоростей деформаций. Изотропная часть тензора

подсеточных напряжений вычисляется следующим образом: т kk = 2 р C I A ² | S | , где параметр C I = 0,09 [3].

В данной работе полагается C_S = 0,15 [4]; ширина фильтра рассчитывается по формуле А = ( A x 1 A x ₂ A x ₃ )^1/3 = V ^1/3 , где A x 1, A x ₂ , A x ₃ — размеры ячеек сетки по соответствующим осям; подсеточное число Прандтля составляет Pr _sgs = 0,4 (взято на основании результатов прямого численного моделирования [5]); число Прандтля — Pr = 0,7 ; подсеточное число Шмидта — Sc _sgs = 0,4 , (выбрано исходя из данных, приведенных в работе [6]); число Шмидта — Sc = 0,7 .

Энтальпия и температура в системе (1) связаны соотношением а C_p — его удельная теплоемкость при постоянном давлении. дополняется фильтрованным уравнением состояния p = р RT , где R

h = C p T , где T — температура газа, Для замыкания система уравнений

— удельная газовая постоянная.

3.    Модель горения

Для численного исследования протекания химической реакции в турбулентном реагирующем потоке одной из используемых моделей является модель Сполдинга (Eddy-Break-Up — EBU), предложенная в работе [7]. Согласно этой модели скорость химической реакции пропорциональна интенсивности турбулентного перемешивания. Однако EBU модель не учитывает влияние температуры потока на скорость протекающих химических реакций и поэтому не позволяет моделировать течения с переходными режимами горения, определяющими условия существования пламени.

Расширить возможности модели и учесть различные режимы течения позволяет модифицированная модель, основой которой является совместное использование модели Сполдинга и кинетической модели. Кинетическая скорость реакции определяется следующей формулой [8]: tv kin = A K р ² ё f C_o x exp |^- eJ ( R_unT ) J , где A_K — постоянный коэффициент, E — энергия активации химической реакции, R_un — универсальная газовая постоянная; для метано-воздушной смеси A K = 1,0 - 10 ¹⁰ м³/(кгс) и E = 1,53 - 10 ⁵ Дж / моль. Скорость турбулентного горения, согласно EBU модели, вычисляется по формуле:

где б — скорость диссипации кинетической энергии турбулентности; к — удельная кинетическая энергия турбулентности; A_EBU — коэффициент модели, A_EBU = 4,0.

При использовании модели EBU совместно с методом крупных вихрей отношение б/к вычисляется так [9, 10]: б/к = ^2 S_yS_v ; тогда формула (2), соответственно, принимает вид

^W t = A EBU Р | ^S | min { c f , c ox Л} .                                         ⁽³⁾

Для учета зависимости скорости реакции w_t от температуры потока формула (3) модифицируется следующим образом:

^W t = A EBU B EBU^Р | ^S | min { c f , c ox /v} ,                                      ⁽⁴⁾

где B_EBU — зависящий от температуры коэффициент: B_EBU = 6,386-10 ³ exp [- eJ ( R un T ) ] .

Вид связи B_EBU и температуры выбран по аналогии с законом Аррениуса. Коэффициент B_EBU меняется в диапазоне от 0 до 1. Максимальное значение ( B EmaU = 1) он принимает при T_ma x ® 2100K (то есть при наибольшей температуре горения метана в воздухе). Следовательно, при температуре, близкой к наибольшей, значения, полученные по формулам (3) и (4), становятся фактически одинаковыми. Коэффициент 6,386 - 10 ³ в выражении для B_EBU найден из соотношения B EBOU /exp [- Ej ( R un T max ) ] = 6,386 - 10 ³ . При уменьшении температуры метано-воздушной смеси коэффициент B_EBU также начинает уменьшаться, обуславливая тем самым зависимость скорости реакции от температуры.

После вычисления кинетической w kin и турбулентной w , скоростей горения скорость реакции окончательно определяется выражением, аналогичным формуле Щёлкина [11]: w = ^w In + w 2 . Применение данной формулы дает возможность моделировать асимптотический переход от турбулентного к ламинарному режиму горения при уменьшении интенсивности турбулентного перемешивания и, наоборот, от ламинарного режима к турбулентному, соответственно, при увеличении интенсивности. Таким образом, предложенная модель может быть использована для расчета течений реагирующего газа в широком диапазоне чисел Рейнольдса.

4.    Вычислительный алгоритм

Для численного решения системы уравнений (1) применялся метод конечных объемов. Пространственная дискретизация уравнений сохранения импульсов проводилась с использованием противопоточной разностной схемы третьего порядка точности QUICK для конвективных членов и центрально-разностной схемы второго порядка точности для диффузионных членов и члена, включающего давление. Алгоритм вычислений подробно описан в работе [12]. Пространственная дискретизация диффузионных членов уравнения энергии и уравнений концентраций осуществлялась также на основе центрально-разностной схемы второго порядка точности, а конвективных членов этих уравнений — по схеме SHARP [13], обладающей большей монотонностью и устойчивостью по сравнению со схемой QUICK. Повышенные требования к монотонности и устойчивости разностной схемы для аппроксимации конвективных членов уравнения энергии и уравнений концентраций объясняются наличием в данных уравнениях источниковых членов, связанных с протеканием химических реакций.

Система уравнений (1) дискретизировалась по времени методом дробных шагов [14, 15], модифицированным для расчета сжимаемых течений (далее символы «–» и «~» опускаются). На каждом шаге по времени метод включал два этапа. На первом этапе из численного решения уравнения сохранения импульсов находились приближенные значения компонент скорости u_i ^* . Необходимые для вычислений значения плотности и давления брались с предыдущего временного слоя, то есть р n и p n . Для дискретизации уравнений сохранения импульсов по времени на этом этапе применялась гибридная явно-неявная схема второго порядка точности [16]. Конвективные члены (оператор F ) вычислялись по явной схеме Адамса–Бэшфорта, а диффузионные (оператор L ) — неявно, по схеме Адамса–Мултона:

р u (Р u) + [3 F (un) - - F (un-1 )1 + [- L (u *)+- L (un )1+H (pn) = 0, t               2 i            2 i                  2 i            2 i                 i где верхний индекс n — номер слоя по времени; операторы, соответственно, описывались выражениями:

5(p uu, F ( u ) = -(^ *^v ’       5 xj-

)            5 С

• -, L ( u ) = ^- ( ц+ц sgs )

5 xj ^x '

5 ui   5 uj   2

• —--+ —--Л 5 i, ——

5x,   5x   3

jik

—

1 5т „ , x   5 p                 5

^k, , H i ( p ) = Оператор —-

3 5 x j                5 x i                   5 x j

означает конечно-разностное приращение.

На втором этапе, называемом шагом коррекции давления, вычислялась поправка давления p ‘ . Величина самого давления на n + 1 шаге по времени находилась по формуле: p ^{n +1} = p ⁿ + p ' . Далее, с учетом приближенных значений скорости u * и поправки давления p ‘ вычислялись откорректированные

.

значения компонент скорости u i

В завершение определялось значение энтальпии метано-воздушной смеси h n ⁺¹ (путем численного

(из решения уравнений концентраций). использовалась схема Кранка–Николсона

интегрирования уравнения энергии) и значения c f ⁺¹ и c nx⁺¹ Для дискретизации данных уравнений по времени с шагом д t

( P h ) n ⁺1

Д t

⁽ P ^h ) n ₊

операторам

5 x j L

Ц

Pr

1 F ( u n ⁺¹ , h n ⁺¹) + 1 F ( u n , h n )

2 L ( u n +1 , h n +1) + 2 L ( u n , h n ) + H ( p

5 ( p uh )             5

соответствовали выражения: F ( u , h ) = ^     , L ( u , h ) =

"

P sgs J

5 h ' 5 x,

⁺ <7 chem , ^H ( P ^^ p 5 t

.

•^{n +1} , pⁿ ) = 0 ,

где

f <5 u i   5 u ,   2, 5 u_k ) )

ц--1----5 i,----- u ,-    +

I 5 x j   5 x i   3     5 x k

' k J

Для уравнения концентрации

горючего схема дискретизации

по времени имела вид:

( p c f ) ^{n +1 —}( p c f )

д t

⁺ 2 F ⁽

n +1      n +1

u , c_f

) + 2 ^F ( u n , C fn

) + 2 L ( c /⁺¹) + 2 L ( c;

) = 0, где    F ⁽ u , c

5 ( p u , C f ) f ^{) =}^ x r

L(c/ =

^{V n} 5 x,

¹J W

Ц

Sc

Ц sgs ) ^{5 c}

Sc sgs J

5 x

)

■ — w . Дискретное уравнение концентрации окислителя находилось аналогично.

На основе полученного значения h n ⁺¹ устанавливалась температура T n ⁺¹ и пересчитывалось зависящее от неё значение плотности p ^{n +1} в соответствии с уравнением состояния p ^{n +1} = p ^{n +1} Д RT ^{n +1}) .

5.    Граничные и начальные условия

Для расчетной области, приведенной на рисунке 1 и имеющей показанные там же геометрические размеры, использовались граничные условия при x ₃ = 0: u ₃ ( x 1 , x ₂ ) = u f , если x 1 e S f , x ₂ e S f ; u ₃ ( x 1 , x ₂ ) = u p , если x 1 e S_p , x ₂ e S_p ; u ₃ ( x 1 , x ₂ ) = u_a , если x 1 e S a , x ₂ e S a , при этом S_$ = a , S_p = a 2 — S_$ , S a = a ² — S_$ — S_p , то есть считались известными значения продольной компоненты вектора скорости для втекающего потока горючего — u_f , потока смеси, стабилизирующей горение, — u_p , и потока воздуха — u_a . Также на рисунке приведена скорость бокового потока воздуха u_wnd . Во входном сечении ( x 3 = 0) для всех потоков значения поперечных компонент вектора скорости принимались равными нулю: u 1 ( x 1 , x ₂ ) = u ₂ ( x 1 , x ₂ ) = 0,

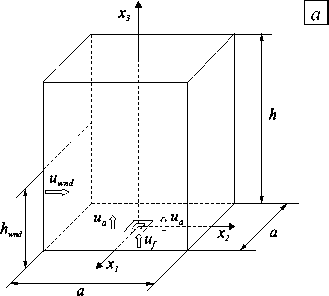
Рис. 1. Схемы расчетной области ( а ) и горелки (стрелками показано направления движения газовой смеси) ( б )

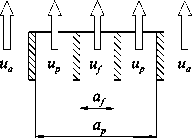
б

а температура смеси и давление были следующими: T(x1, x2) = T0; p (x1, x2) = p0. Концентрации горючего Cf и окислителя cox на входе равнялись: Cf (x1, x2) = Cf 0 и cox (x1, x2) = cox0 при x1 e Sf,  x2 e Sf ; Cf (x1, x2) = 0 и cox (x1, x 2) = 0 при x1 e Sp , x 2 e Sp ; cf (x1, x 2) = 0 и cox (x1, x 2) = coxa при x1 e Sa , x 2 e Sa •

При расчете турбулентных течений важное значение имели граничные условия на выходной границе расчетной области, так как волны давления, генерируемые в ней вихревыми структурами потока, должны выходить наружу без отражения. Поэтому на верхней границе области, определяемой как выходная граница, использовалось условие, называемое условием конвективного переноса (или неотражающим граничным условием [2]): x3 = h: дФ/д t + ubor дФ/д n = 0, где Ф — любая из искомых функций, ubor — величина нормальной скорости на границе. На боковых границах для переменных задавались условия нулевого нормального градиента: x1 = 0, x1 = a, x2 = 0, x2 = a : дФ/дn = 0 .

В качестве начальных распределений (при t = 0) принимались следующие:

u 1 ( x 1 , x ₂ , x 3 ) = u ₂ ( x 1 , x ₂ , x 3 ) = u ₃ ( x 1 , x ₂ , x 3 ) = 0;        p ( x 1 , x ₂ , x 3 ) = p ₀ ;

T ( x i , x 2 , x 3 ) = T _o ;

C f ( x 1 , x ₂ , x ₃ ) = 0,

C ox ( x i , x 2 , x 3 ) = C oxa .

• 6.    Результаты

  • 6.1. Моделирование диффузионного пламени

    Для тестирования предложенной методики использовались экспериментальные данные по турбулентному метано-воздушному диффузионному пламени — Sandia flame D [17]. В этой серии экспериментов менялась скорость потока подаваемого горючего при неизменных размерах горелки. Для пламени Sandia D поток имел число Рейнольдса Re = 22400 , которое вычислялось по формуле: Re = p u_fa_f /ц . Топливом являлась смесь метана и воздуха в соотношении 25% и 75% по объему (соответственно 15,6% и 84,4% по массе). В таких условиях течения пламя горит как диффузионное, поскольку в богатой метаном смеси реакции не протекают.

В расчетах использовались следующие значения параметров задачи: a = 1,0м , h = 1,0м — размеры расчетной области; af = 6,4 мм, ap = 16,2 мм — размеры горелки; Uf = 49,6 м/с — скорость горючего; up =11,4 м/с и ua =0,9 м/с — скорости потока, стабилизирующего горение, и воздуха; скорость бокового потока воздуха uwnd = 0 м/с; температура T0 = 294K ; давление p0 = 100610 Па (0,993 атм); концентрации горючего и окислителя, соответственно, Cf0 = 0,156, Cox0 = 0,177 и Coxa = 0,21. Экспериментальные данные по серии пламен Sandia представлены на сайте

Сходимость численного решения проверялась с использованием трех разностных сеток с числом узлов, соответственно, 25 х 25 х 50, 50 х 50 х 100 и 100 х 100 х 200 . Во всех случаях имеют место качественно близкие результаты. Наименьшая погрешность (отличие от результатов эксперимента) соответствует третьей сетке. Расчеты с более мелкими сетками не проводились в виду низкой вычислительной производительности имеющегося компьютера.

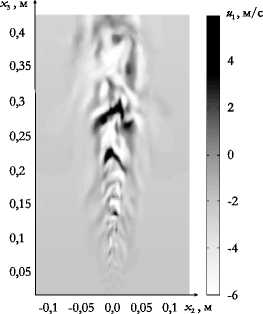
Далее приводятся результаты, полученные на сетке 100 х 100 х 200. На рисунке 2 показано распределение температуры турбулентного диффузионного пламени и составляющей скорости u ₁ в плоскости { x ₂ , x 3} при x 1 = 0 для момента времени t = 1 c .

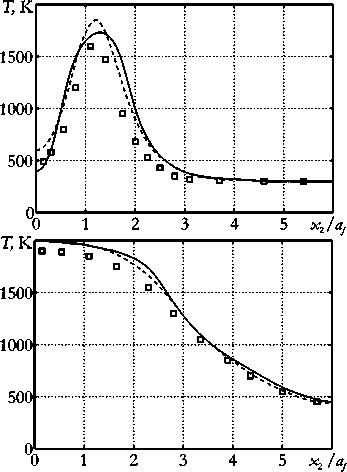
Рисунки 3 и 4 демонстрируют результаты расчетов по предложенной методике: на рисунке 3 приведены осредненные по времени распределения температуры пламени в трех поперечных сечениях и в направлении оси x ₃ , на рисунке 4 — распределения продольной компоненты скорости u ₃ и концентрации горючего в направлении оси x ₃ . Также на рисунках показаны экспериментальные данные из работы [17] и результаты моделирования с применением Flamelet модели горения [6]. Хорошее совпадение авторских результатов моделирования с экспериментальными данными и результатами моделирования, полученными в [6], подтверждают достоверность предложенной методики.

В работе [18] исследовались характерные особенности гидродинамических течений с точечным источником. В рассматриваемом здесь случае источник вдува горючего компонента с поверхности представляет собой квадрат со стороной a f и включает в себя 10 х 10 ячеек расчетной сетки. Отметим, что аппроксимация круглого сечения квадратным (при равной массовой скорости вдува) является правомерной, что подтверждается сравнением результатов моделирования с экспериментальными данными, представленными на рисунках 3, 4.

Рис. 2. Распределение температуры ( а ) и составляющей скорости u ₁ ( б )

а

а

в

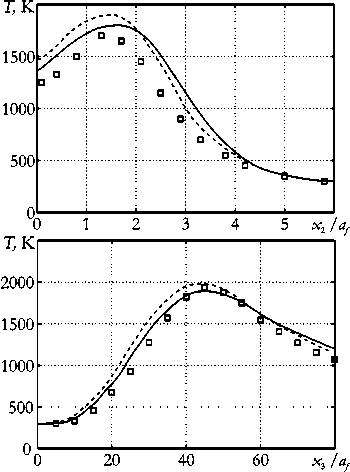
Рис. 3. Распределение температуры в трех поперечных сечениях диффузионного пламени x ₃ Ia_f : 15 ( а ), 30 ( б ), 45 ( в ),

б

г

и распределение температуры в направлении оси x ₃ ( г ) (сплошная линия – результаты расчетов по предложенной методике, □ – эксперимент [17], пунктирная линяя – результаты работы [6])

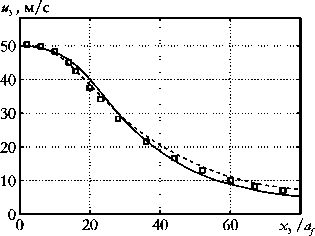
а

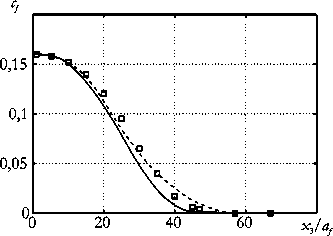
Рис. 4. Распределение продольной скорости u ₃ ( а ) и концентрации горючего c_f ( б ) в направлении оси x ₃ ; сплошная линия – результаты расчетов по предложенной методике, □ – эксперимент [17], пунктирная линяя – результаты работы [6])

б

• 6.2. Моделирование перехода от ламинарного режима горения к турбулентному

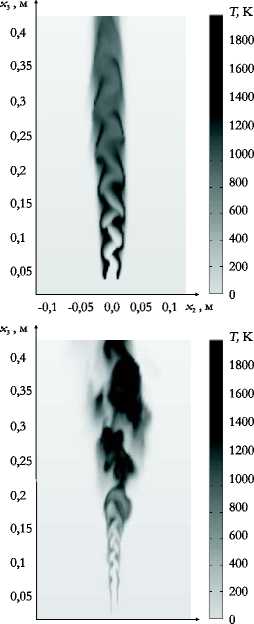
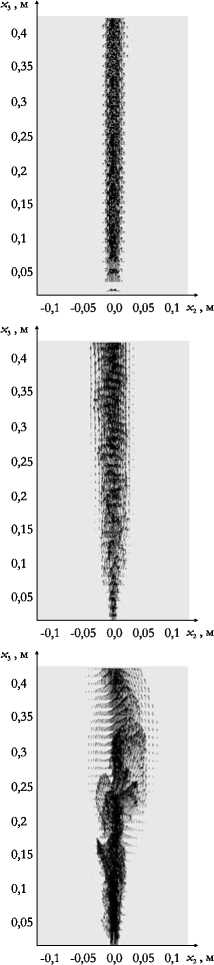
  Моделирование метано-воздушного диффузионного пламени осуществлялось при различных значениях числа Рейнольдса. Расчеты пламени выполнены для трех скоростей потока u_f , соответствующих числам Рейнольдса Re = 50, 135 0 , 9 000 . Число узлов разностной сетки и размеры расчетной области не изменялись в процессе исследования и были такими же, как в пункте 6.1. Скорости потоков u_p , u a и u_wnd задавались равными нулю.

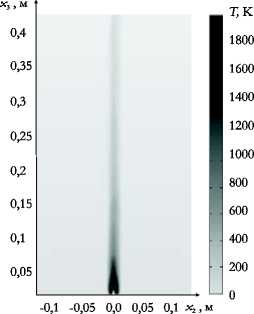
а

-0,1 -0,05 0,0 0,05 0,1 Х2,м

в

д

б

г

е

Рис. 5. Распределение температуры ( а , в , д ) и поле скорости ( б , г , е ) для потоков с числами Рейнольдса Re: 50 ( а , б ), 1350 ( в , г ), 9000 ( д , е )

На рисунке 5 представлены распределение температуры пламени и поле скорости в плоскости { x 2 ,x 3} , полученные в результате численных расчетов диффузионного пламени по предлагаемой методике. Из рисунка видно, как меняется режим горения с увеличением числа Рейнольдса: при Re = 50 процесс горения протекает ламинарно, при Re = 1350 наблюдается переходный характер, и в третьем случае, при Re = 9000 , горение становится турбулентным.

• 6.3. Моделирование срыва (прекращения горения) турбулентного диффузионного пламени

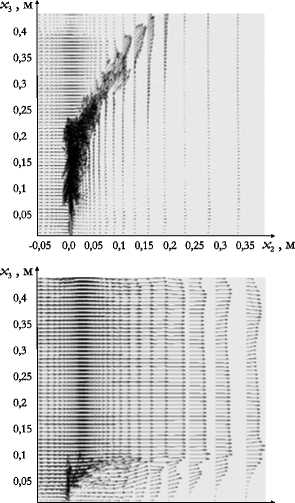
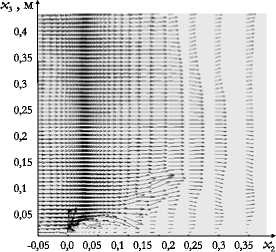
  Моделирование срыва диффузионного пламени проводилось для потока с числом Рейнольдса Re = 9000 . Число узлов разностной сетки и размеры расчетной области были такими же, как и в двух предыдущих расчетах (пункты 6.1 и 6.2). Скорости потоков u_p и u_a задавались равными нулю, скорость бокового потока воздуха u_wnd (в направлении оси x ₂ ) плавно увеличивалась от нуля до величины, при которой происходило прекращение процесса горения. Размер бокового потока составлял h wnd = 0,4 м.

0,4

0,35

0,3

0,25

0,2

0,15

0,1

0,05

т,к

о

а

-0,05 0,0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 Х2 , М

т,к

О

в

-0,05 0,0 0,05 0,1 0,15 0,2 0,25 0,3 0,35 X, , М

б

г

д

е

Рис. 6. Распределение температуры ( а , в , д ) и поле скорости ( б , г , е ) при скорости бокового потока u_wnd , м/с: 0,5 ( а , б ); 3,0 ( в , г ); 5,0 ( д , е )

На рисунке 6 представлены распределение температуры пламени и поле скорости в расчетной области при различных значениях u_wnd . Критерием момента погасания пламени являлось прекращение химических реакций. Критическое значение скорости бокового потока воздуха, при котором пламя погасло, составило u_wnd ≈ 5,5м/с.

7.    Выводы

Предложен и реализован алгоритм моделирования дозвуковых турбулентных течений вязкого реагирующего газа, основанный на методе крупных вихрей. Результаты расчетов, проведенных по предложенной методике, хорошо согласуются с экспериментальными данными и результатами численного моделирования, взятыми для сравнения в работах других авторов.

Выполнено параметрическое исследование диффузионного пламени для различных скоростей потока горючего, позволяющие оценить значение числа Рейнольдса, при котором происходит переход от ламинарного режима горения к турбулентному.

Проведено моделирование диффузионного турбулентного горения с наличием бокового потока воздуха, итогом которого стало определение значения критической скорости бокового потока, при которой происходит погасание пламени.

Полученные результаты позволяют сделать вывод, что предложенный алгоритм может быть использован для моделирования течений с переходными режимами горения, определяющими условие погасания пламени.