Численное моделирование ударных волн в неравновесном химически активном газе

DOI:

Структура слабых ударных волн в неравновесном колебательно-возбужденном газе рассматривалась в работах [2; 7; 9; 10] на основе акустического уравнения с квадратичной нелинейностью. Подход, основанный на решении нелинейного акустического уравнения используется и при исследовании нелинейных волновых структур в различных неравновесных средах, например, с неравновесным тепловыделением [3; 11].

В общем динамика нелинейных волн со значительной амплитудой требует учета не только квадратичной нелинейности, но и нелинейных поправок более высокого порядка. Полный учет всех нелинейных эффектов возможен только при прямом численном решении газодинамических уравнений. Ранее детальное исследование динамики акустической неустойчивости и ударных волн в неравновесном химически активном не проводилось.

1.    Постановка задачи и численная модель динамики неравновесного химически активного газа

Рассмотрим задачу сверхзвукового натекания газа на препятствие (твердую стенку). Воспользуемся математической моделью динамики неравновесного колебательновозбужденного газа с учетом химических реакций, вязкости, теплопроводности, нагрева и охлаждение, которая подробно описана в работе [4].

1.1.    Численная модель

Проведем обобщение численной модели динамики неравновесного колебательновозбужденного газа [5; 6] на случай химической активности газа. В обобщенной модели добавляется новое уравнение динамики химически активного реагента [4], а в уравнении баланса энергии удельная мощность нагрева дополняется новым слагаемым (см. [4]), которое учитывает нагрев газа за счет химических реакций.

Для решения уравнений обобщенной численной модели воспользуемся хорошо апробированными газодинамическими методами сквозного счета CSPH-TVD/MUSCL, которые адаптированы для моделирования динамики химически активных сред и позволяют исследовать как нелинейную динамику акустической неустойчивости, так и структуру ударных волн.

1.2.    Нелинейное акустическое уравнение

Наряду с обобщенной численной моделью полной системы уравнений газодинамики неравновесного химически активного газа (см. пп. 1.1) рассмотрим приближение, в котором учитываются только квадратичные поправки по возмущенным величинам. Этот подход используется при выводе нелинейного акустического уравнения, широко применяемого для исследования структуры ударных волн в различных неравновесных средах [2; 3; 7; 9–11]. Для того, чтобы получить аналог нелинейного акустического урав- нения в рамках нашей обобщенной численной модели необходимо в выражениях для по- токов импульса и энергии исключить кубические поправки относительно возмущенных величин f = f — f0 (fo — начальные стационарные значения параметров течения):

^и ~~2

Fu = QU + р — ^0^7--QU , ox

. ди

F _e = (Е + р)и — p₀QU 77- дх

дТ      ди

^{— к} 0 + 0qQ^u ^- , дх       дх

где F _u и F _e — потоки импульса и энергии для модели с квадратичной нелинейностью соответственно. Также необходимо заменить функции общего вида f ( q, Т ) для времени колебательной релаксации т , скорости химической реакции К , мощности нагрева Q и охлаждения Л следующей квадратичной аппроксимацией:

̃︀

̃︀

f (Q,T )

Q / д lnf \    Q ² / д ² ln f \ Т / д ln f \ Т ² / д ² ln f \

Q 0 дм 0 ⁺ q 0 дм ² 0 ⁺ Т дШТЛ ⁺ Т ² дlnT ²)

̃︀

̃︀

= i^f‘ ⁺

О ² Т

Q 0 ^f _&& + —^f T +

̃︀

Т 2 hr.

^Т 0

Предложенный подход (1)–(2) обладает рядом преимуществ по сравнение с аналитическим представлением нелинейного акустического уравнения и прямыми численными методами его решения. Во-первых это универсальность, позволяющая рассматривать различные неравновесные среды, а во-вторых это использование хорошо апробированных численных газодинамических методов, которые обладают свойствами консервативности, устойчивости и отсутствием паразитных осцилляций в численных решениях за счет использования TVD-ограничителей [5; 6].

2.    Результаты численного моделирования

Будем рассматривать три режима натекания неравновесного химически активного газа: дозвуковой с числом Маха М <  1 , околозвуковой М =1 и сверхзвуковой М >  1 . Далее будем использовать безразмерные параметры, определенные в [5; 6]. Базовые фиксированные значения безразмерных параметров численной модели зададим в виде [4–6]: Y = 1 , 4 , С . = 0 , 0888 , S 0 = 0 , 5 , т 0 “ ) = 1 , Р 0 \ = 10 ^-4 , т , = —1 , т т = —4 , 3333 , Q ,^a,s) = 0 , qT = 0 , qT = 10 , Q ^ = 1 , Л , = 0 , Л _т = 1 , 4286 . Варьируемые параметры численной модели: число Маха М = {0 , 5;1;2} ; доля химического энерговыделения в общей мощности нагрева в = {0; 0 , 5} . Расчетную область X Е [0 , L ] ( L = 500 ) покроем сеткой с размером ячеек h = L/N , где количество ячеек N = 5 х 10 ⁴ . Выбранное пространственное разрешение ( h = 0 , 01 ) позволяет детально исследовать структуру ударных волн (УВ) и мелкомасштабных неустойчивых возмущений, генерируемых фронтом УВ. Даже для самых мелкомасштабных неустойчивых гармоник, возникающих в численных экспериментах, количество ячеек, приходящихся на длину волну, оказывается больше 50. Твердая стенка расположена в точке X = 0 , а газ натекает на нее справа со скоростью и ₀ = —М .

2.1.    Нелинейная динамика акустической неустойчивости в неравновесном химически активном газе

В обычной равновесной и диссипативной среде при дозвуковом натекании газа на препятствие нелинейные волновые структуры с ударными волнами не образуются, а образуется только некоторое гладкое возмущение в виде звуковой волны, которое затухает при удалении от твердой стенки. В неравновесном колебательно-возбужденном газе, параметры которого допускают развитие акустической неустойчивости [1; 4; 8], ситуация кардинально меняется. Начальное звуковое возмущение быстро эволюционирует в ударную волну, за счет развития акустической неустойчивости, рисунке 1 при t = 20. Далее фронт этой ударной волны начинает генерировать возмущения конечной амплитуды, которые, также за счет развития акустической неустойчивости, эволюционируют в систему ударно-волновых импульсов (УВИ) [5; 6] (рис. 1 при t = 500 и t = 390).

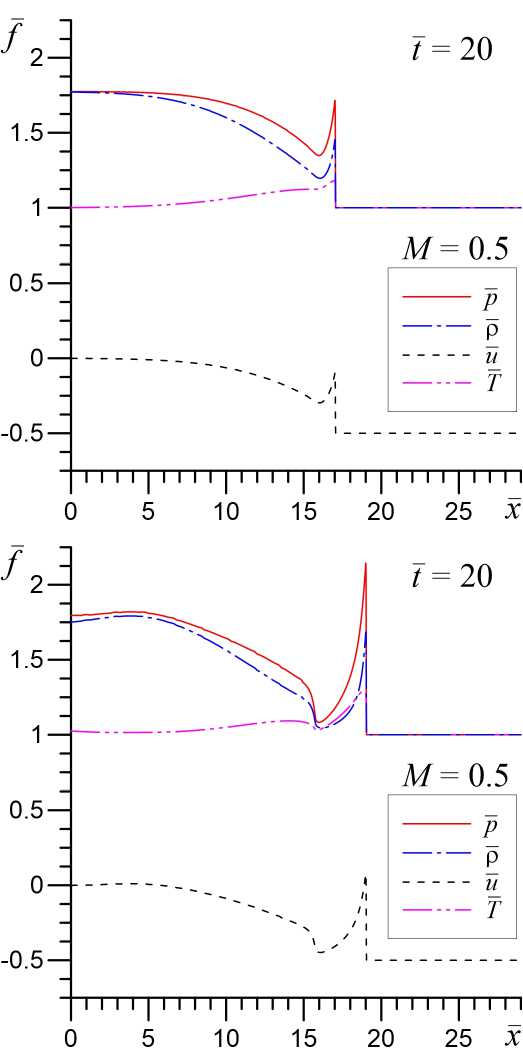
Рис. 1. Структура ударных волн при начальной скорости натекания газа М = 0 , 5 в различные моменты времени. Верхний ряд соответствует модели без учета химический реакций ( в = 0), а нижний ряд — при в = 0 , 5

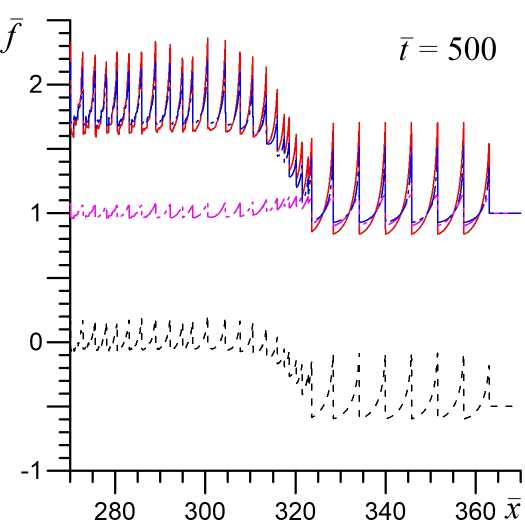
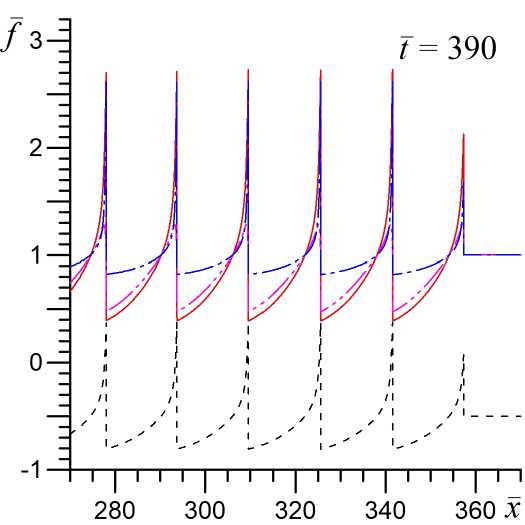
На рисунке 1 показана динамика образования УВИ как для модели без учета химической активности газа (в = 0), так и для модели с учетом химических реакций (в = 0, 5). Видно, что в неравновесном химически активном газе происходит существенное усиление акустической неустойчивости и на конечной нелинейной стадии ее эволюции формируются ударно-волновые импульсы с интенсивностью в 2–2,5 раза больше, чем без учета химических реакций. При этом пространственным масштаб (расстояние между фронтами) УВИ также увеличивается в 2–2,5 раза. Скорость распространения УВИ (скорость первого фронта волнового пакета) относительно невозмущенного газа составляет ush — 1, 22 для модели с в = 0 и ush — 1,44 при в = 0, 5, то есть натекание газа на фронт УВИ происходит со сверхзвуковой скоростью. Увеличение интенсивности и пространственного масштаба УВИ в неравновесном химически активном газе обусловлено усилением акустической неустойчивости при учете химических реакций. Наибольший эффект увеличения акустического инкремента происходит на частотах D ~ 1 [4], чем и обусловлено увеличение пространственного масштаба УВИ.

2.2.    Структура и устойчивость ударных волн в неравновесном химически активном газе

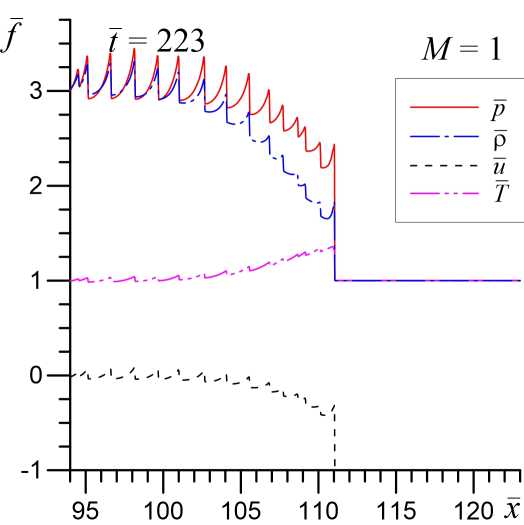
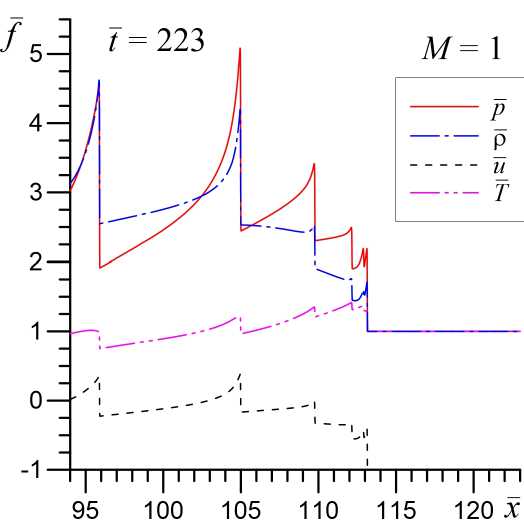
В обычной равновесной и диссипативной среде при околозвуковом и сверхзвуковом натекании газа на препятствие происходит образование ударных волн, которые распространяются от твердой стенки с практически неизменной формой, а за фронтом УВ устанавливается стационарное течение. При околозвуковых режимах натекания образуются слабые ударные волны М ~ 1 , 01 -1,05. Для околозвуковых и сверхзвуковых режимов натекания в неравновесном колебательно-возбужденном газе, параметры которого допускают развитие акустической неустойчивости [1; 4; 8], ситуация также кардинально меняется. На фронте ударной волны, образовавшейся за счет газодинамических процессов, формируется характерный пик, обусловленный развитием акустической неустойчивости (рис. 2 при t = 30 ). Далее фронт ударной волны с этим пиком начинают генерировать звуковые волны, которые также за счет развития акустической неустойчивости эволюционируют в систему УВИ [5; 6], которая формируются за фронтом головной ударной волны (см. рис. 2 при t = 223 ).

На рисунке 2 показана динамика и структура ударных волн для случая околозвукового натекания газа М =1 в моделях без учета химической активности газа ( в = 0 ) и с учетом химических реакций ( в = 0 , 5 ). Видно, что в неравновесном химически активном газе происходит существенное усиление акустической неустойчивости за фронтом головной ударной волны, что на конечной нелинейной стадии ее эволюции приводит к образованию более интенсивной системы УВИ с амплитудой в 2–5 раз больше, чем без учета химических реакций. Пространственный масштаб УВИ также увеличивается в 2–5 раз. Скорость распространения головной ударной волны относительно невозмущенного газа незначительно возрастает при учете химической активности среды. Так при в = 0 она составляет u _s h — 1 , 48 , а при в = 0 , 5 имеем u _s h — 1 , 5 . Также как и для случая дозвукового натекания увеличение интенсивности и пространственного масштаба УВИ за фронтом головной ударной волны связано с более высоким значением акустического инкремента в неравновесном химически активном на частотах D ~ 1 [4].

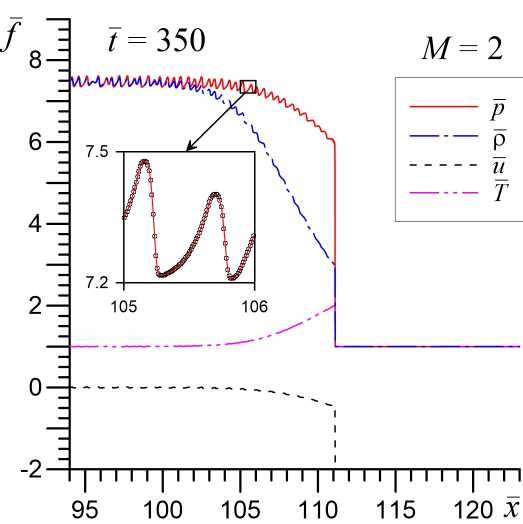
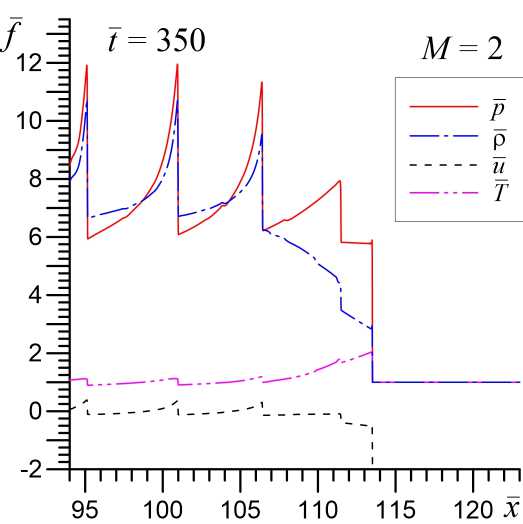
На рисунке 3 показана динамика и структура ударных волн для случая сверхзвукового натекания газа М = 2 в моделях без учета химической активности газа ( в = 0 ) и с учетом химических реакций ( в = 0 , 5 ). Видно, что при сверхзвуковом режиме натекания образуется ударная волна с большей амплитудой, характерный пик на фронте УВ, обусловленный акустической неустойчивостью, становится существенно меньше как по интенсивности, так и по пространственному масштабу (рис. 3 при t = 50 ). В этом численном эксперименте скорость распространения головной ударной волны относительно невозмущенного газа составляет u _s h — 2 , 31 .

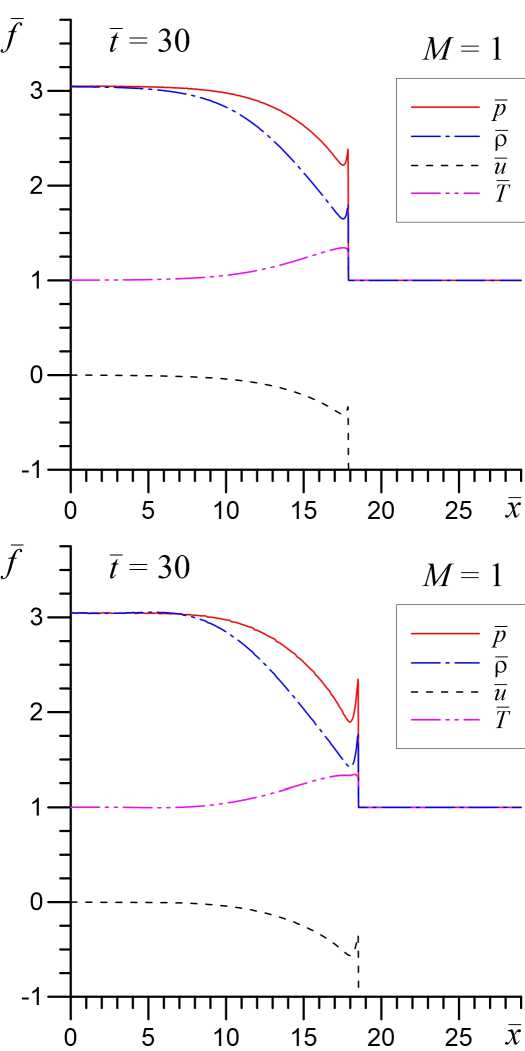
Рис. 2. Структура ударных волн при начальной скорости натекания газа М = 1 в различные моменты времени. Верхний ряд соответствует модели без учета химический реакций ( в = 0), а нижний ряд — при в = 0 , 5

Последующая эволюция структуры ударных волн сильно зависит от параметра β . Так при в = 0 к моменту времени t = 350 за фронтом головной ударной волны образуется мелкомасштабна волновая структура с относительной амплитудой возмущений ~ 10 %, то есть происходит существенное уменьшение акустического инкремента. В модели с учетом химической активности газа в = 0 , 5 при М = 2 стабилизация (уменьшение инкремента) неустойчивости не происходит и также за фронтом головной УВ формируется система интенсивных УВИ с большим пространственным масштабом. Дальнейшее увеличение числа Маха в натекающем газе приводит к полной стабилизации неустойчивости акустического типа за фронтом головной УВ при М > M _crit . Для модели с в = 0 критическое число Маха составляет M _crit ^ 3 , а для модели с в = 0 , 5 имеем M _crit ~ 7 . Величина M _crit возрастает с увеличением начальной степени неравновесности S 0 .

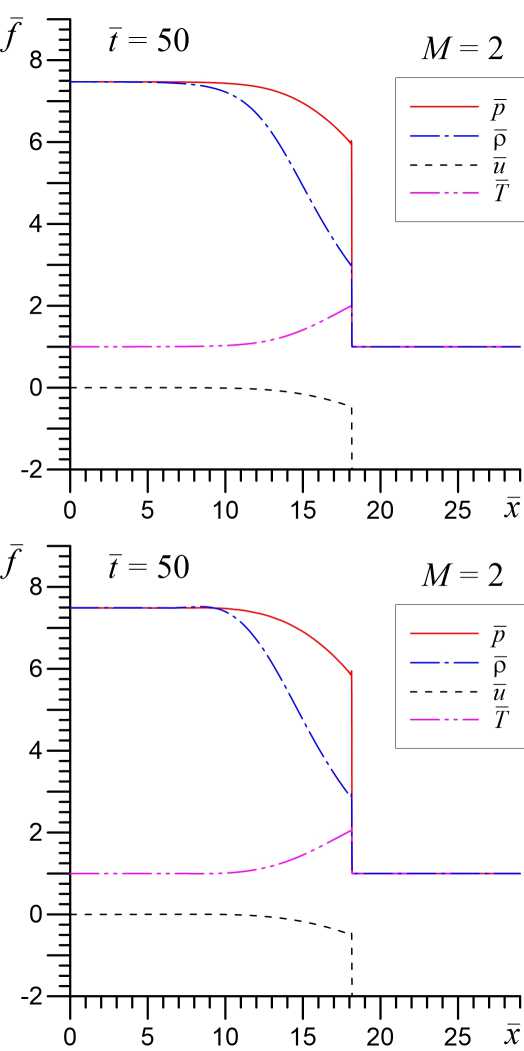
Рис. 3. Структура ударных волн при начальной скорости натекания газа М = 2 в различные моменты времени. Верхний ряд соответствует модели без учета химический реакций ( в = 0), а нижний ряд — при в =0 , 5. На врезке показана структура мелкомасштабных неустойчивых гармоник, генерируемых фронтом УВ, узлы расчетной сетки отмечены точками

Заключение

Сформулируем основные результаты работы:

• 1)    Построена обобщенная численная модель динамики неравновесного колебательновозбужденного газа с учетом вязкости, теплопроводности и химических реакций. В обобщенной модели добавилось новое уравнение динамики химически активного реагента, а в уравнении баланса энергии удельная мощность нагрева дополнена новым слагаемым, учитывающим нагрев газа за счет химических реакций.

• 2)    Разработан программный комплекс для моделирования динамики неравновесных химически активных сред, который основан на газодинамических методах сквозного счета CSPH-TVD/MUSCL и предназначен как для исследования нелинейной

динамики акустической неустойчивости, так и для изучения структуры и устойчивости ударных волн в неравновесных химически активных средах.

• 3)    Исследовано влияние химической активности в неравновесном колебательно-возбужденном газе на нелинейную динамику акустической неустойчивости. Показано, что учет химических реакций в неравновесном газе приводит к усилению акустической неустойчивости и в результате на конечной нелинейной стадии формируются ударно-волновые импульсы (УВИ) более высокой интенсивности и с большим пространственным масштабом. Увеличение интенсивности и пространственного масштаба УВИ связано с более высокими значениями акустического инкремента на частотах шт ~ 1 по сравнению с моделями без учета химических реакций.

• 4)    Проведено численное моделирование ударных волн в неравновесном колебательновозбужденном газе с учетом химических реакций, вязкости, теплопроводности, нагрева и охлаждения. Исследована структура и устойчивость ударных волн (УВ) различной интенсивности (от слабых УВ с числом Маха М <  1 , 01 до сильных УВ с М >  10 ). Показано, что ударные волны в неравновесном колебательновозбужденном газе оказываются неустойчивыми, то есть за фронтом УВ происходит генерация неустойчивых возмущений, амплитуда которых с течением времени нарастает, достигая нелинейного насыщения. С увеличением числа Маха амплитуда и пространственный масштаб, формируемых на нелинейной стадии развития неустойчивости волновых структур за фронтом УВ, уменьшается. При больших значениях числа Маха М > M _crit происходит стабилизация неустойчивости и УВ становятся устойчивыми. Величина M _crit увеличивается с ростом степени неравно-весности S 0 и при учете химических реакций. Кроме того, учет химической активности приводит к увеличению как максимальной амплитуды, так и пространственного масштаба волновых структур, образующих за фронтом УВ на нелинейной стадии развития неустойчивости.

• 5)    Разработана численная модель, которая является аналогом нелинейного акустического уравнения, описывающего динамику возмущений конечной амплитуды в химически активной неравновесной среде с учетом квадратичных поправок. Данная модель строилась на основе базовой численной модели посредством исключения в выражениях для потока импульса и энергии кубических поправок относительно возмущенных величин ( ~ q и 2 ), а также замене функций общего вида f ( q,T ) для времени колебательной релаксации, скорости химической реакции, мощности нагрева и охлаждения квадратичной аппроксимацией с параметрами f _e, fa , f _ee , f iT • Преимуществом данного подхода является универсальность и использование хорошо апробированных численных газодинамических методов, обладающих важными свойствами, такими как консервативность, устойчивость, точность и отсутствие паразитных осцилляций за счет применения TVD-ограничителей. В дальнейшем построенная модель нелинейного акустического уравнения может быть исполь-

• зована для оценок точности и определения границ применимости квадратично-
• го приближения, которое широко применяется для анализа волновых структур

(структуры слабых УВ) в различных средах.