Численное моделирование высокоскоростного ударного воздействия на конструкцию космических аппаратов

федоров м.Ю.

крауС е.и.

Шабалин и.и.

В настоящей работе численное моделирование высокоскоростного ударного воздействия рассматривается по отношению к проблеме техногенного засорения околоземного космического пространства (ОКП), или к так называемой проблеме космического мусора (КМ).

Как известно, появление термина «космический мусор» относится к концу 1980-х гг. Космическим мусором, по определению В. Флюри ( Flury W. ) [1], являются все объекты искусственного происхождения и их части в ОКП, которые не функционируют и не могут служить никаким полезным целям.

За годы освоения ОКП, со времени запуска первого искусственного спутника Земли Советским Союзом 04 октября 1957 г. (параметры орбиты: апогей — 947 км; перигей — 228 км) количество запусков только нарастало. В период с конца 1960-х по 1990-е гг. активность запусков достигла максимума — порядка 100 в год, что, естественно, сопровождалось накоплением КМ в виде как крупных фрагментов, так и мелких частиц [2–5].

Столкновение КМ с элементами конструкции космических аппаратов (КА) может или иметь катастрофические последствия с разрушением значительной части спутника, или вызывать его локальные повреждения. Локальные повреждения не нарушают общую конфигурацию КА (например — пробой элементов систем обеспечения теплового режима КА [6]), однако могут привести или к полной потере работоспособности аппарата, или к утрате некоторых его функций. А в случае ударного воздействия КМ на советские КА с бортовыми ядер-ными энергетическими установками (ЯЭУ) «Бук» и «Топаз», которые прекратили активное существование три десятилетия назад, были потенциально возможны ситуации с образованием осколков, содержащих остаточную радиоактивность, или с падением части реактора на поверхность Земли [7–10].

Чтобы количественно оценивать возникновение фрагментов техногенной природы в ОКП за счёт разрушения КА, а также прогнозировать живучесть КА путём определения граничного размера КМ, опасного для целостности и функционирования КА, а также разрабатывать технические средства защиты, была поставлена весьма амбициозная цель. Она состоит в том, чтобы на основе фундаментальных законов механики сплошной среды создать методики, алгоритмы и, подчеркнём, национальные, российские программные средства, реализующие в масштабе настольного компьютера решение задач высокоскоростного ударного разрушения сложных технических объектов, причём с функцией подсчёта количества образовавшихся осколков и спектров их скоростей.

Высокоскоростное ударное воздействие на материальные объекты сопровождается множеством физических явлений: волновые процессы, разрушение материалов, фазовые переходы. На протекание ударно-волновых процессов существенно влияют начальные условия: скорость взаимодействия (от сотен до десятков тысяч метров в секунду), геометрическая форма (конструкция), состав конструкционных и других материалов соударяющихся объектов.

Задача получения расчётно-теоретическим путём конечного состояния технических объектов типа КА или их энергодвигательных установок после взаимодействия с КМ значительно усложняется за счёт составной разветвлённой конструкции, содержащей широкий набор материалов. В объекте исследования могут присутствовать уникальные композиционные материалы, поведение которых в условиях высоких давлений и температур недостаточно изучены, что выражается, например, в отсутствии соответствующих констант для уравнений, описывающих высокоэнергетические процессы в веществе.

Несомненно, решение может быть получено экспериментальным путём, но организация экспериментов, реализующих скорости в тысячи метров в секунду, само по себе дело непростое и во всех смыслах затратное как при применении баллистических установок, так и метательных систем взрывного действия, причём даже на простых моделях. А при исследованиях на полноразмерных макетах материальные и временные затраты многократно возрастают.

Таким образом, создание программного комплекса, основанного на фундаментальных законах механики сплошной среды применительно к сложным техническим объектам, является наиболее эффективным путём достижения поставленной цели, но, безусловно, при надлежащей верификации, включающей привлечение и экспериментальных данных.

Перейдём к постановке задачи.

Принимаем Лагранжев подход как наиболее подходящий для описания высокоскоростного взаимодействия деформируемых твёрдых тел [11, 12].

Применение Лагранжева подхода обусловлено множеством контактных взаимодействий элементов сложного составного объекта, что естественным образом описывается в данной постановке.

Модель (система уравнений) состоит из уравнений движения, баланса массы, импульса и энергии, а также уравнений состояния и упругопластического течения Прандтля–Рейса: уравнение траектории материальных частиц x.i = ui;

уравнение неразрывности среды

V ₀ρ₀ = V ρ;

закон изменения импульса материальной частицы

.

ρ u _i = σ _ij,j ;

изменение внутренней энергии частицы

ρ e = σ _ij ε _ij ;

тензор скоростей деформаций имеет вид

ε^. _ij = 0,5( u_{i , j} + u_j,i ); тензор напряжений представим в общепринятой форме

σ _ij = –δ _ijP + s_ij , где s_ij — девиатор тензора напряжений, отвечающий за реакцию на сдвиговое формоизменение материальной частицы; δ _ij — символ Кронекера; P — функция давления в форме Ми–Грюнайзена [13].

Уравнения процесса задаём в форме Прандтля–Рейса [11, 12]

s^._ij + d λ′ s_ij = 2 G ε ^. _i ′ _j , где ε ^. _i ′ _j = ε ^. _ij – ε ^. _kk /3

при условии пластичности Губера–Мизеса sij · sij ≤ 2Y02/3, где ρ — плотность; V, V0 — текущий и начальный удельные объёмы; G — модуль сдвига; Y0 — динамический предел текучести; σij — тензор напряжений; e — внутренняя энергия; dλ′ — параметр материала; t — текущее время; s.ij — скорость изменения девиатора тензора напряжений; ε. i′j — девиатор тензора скоростей деформации; ε.ij — тензор скоростей деформации.

Для определения скалярного множителя dλ′   используется известная процедура приведения к кругу текучести [11].   В приведённых выше уравнениях использованы общепринятые обозначения:   каждый из индексов

(i, j) пробегает значения 1,   2; по повторяющимся индексам проводится суммирование; точка над символом — производная по времени; индекс после запятой — производная по соответствующей координате.

Уравнения в частных производных преобразуются в явную разностную схему на треугольной сетке вдоль траектории каждой материальной частицы. Материальная частица — элемент среды (материала), обладающий массой и размерами. В случае нашей модели это ячейка конечноразностной сетки.

Разностная сетка в сложных многосвязных областях генерируется автоматически динамическим способом [14, 15].

Для учёта процессов разрушения система дополняется соотношениями, связывающими параметры напряжённо-деформированного состояния с предельными величинами по отношению к разрушению материалов [12, 16]. В качестве уравнения состояния используется термодинамически полное малопараметрическое уравнение состояния [13, 17, 18], которое отличается тем, что практически все параметры можно найти в справочниках по физико-механическим свойствам материалов. Расчёт контактных поверхностей между взаимодействующими деформируемыми твёрдыми телами осуществляется по симметричному алгоритму [19]. Упомянутые выше разработки реализованы в виде комплекса программ REACTOR 2D [20–22], позволяющего решать плоские и аксиально симметричные задачи механики деформируемого твёрдого тела в широком диапазоне скоростей взаимодействия [8, 16].

Рассмотрим принципиальные схемы построения программного комплекса.

Поскольку в начальных данных задач удара непременно имеет место поле скоростей налетающего тела (ударника), то программа будет иметь принципиальную схему, приведённую на рис. 1.

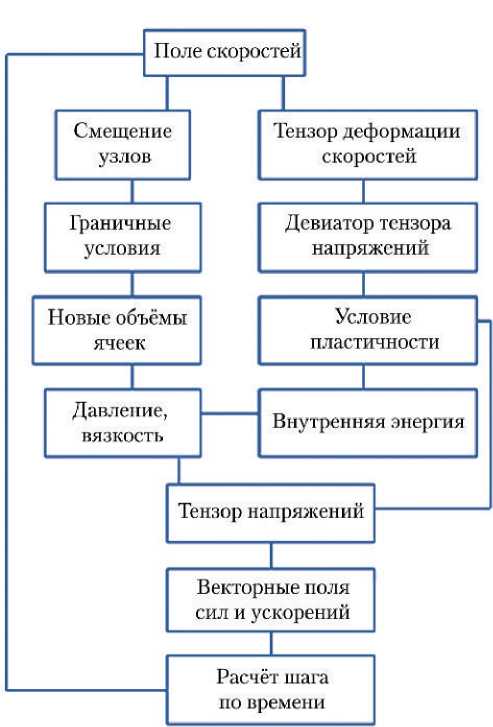
Рис. 1. Принципиальная схема программы

Подробное описание разностных соотношений каждого блока содержится в монографии [12].

Программную реализацию приведённой выше схемы можно представить в виде следующих блоков (рис. 2).

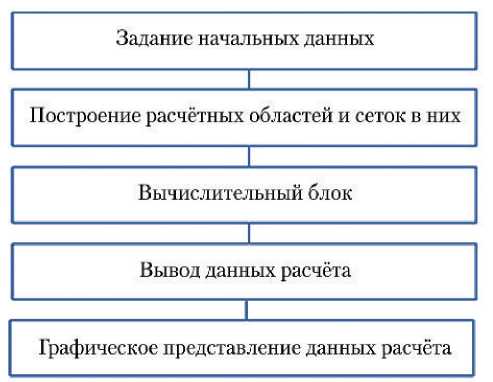
Рис. 2. Блок-схема программы

На рис. 3 представлена схема блока вычислений. По полю скоростей находятся смещения узлов каждой счётной области, свободных от взаимодействия. Затем проверяются граничные условия, т. е. проверяется наличие взаимодействия с жёсткими границами и границами других счётных областей. После чего в едином цикле вычисляются все параметры, отнесённые к ячейкам сетки. Далее в ячейках рассчитываются узловые силы, ускорения и поле скоростей на новом временном слое.

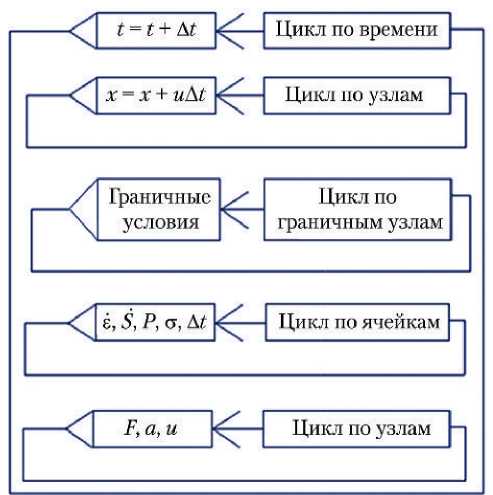
Рис. 3. Схема вычислительного блока

С самого начала разработка программного комплекса REACTOR подразумевала не только получение картины разрушения конструкции в результате высокоскоростного ударного воздействия, но и решение задачи подсчёта образовавшихся осколков с распределением по массам (объёмам) и скоростям.

Для решения указанной задачи были разработаны алгоритм и программный модуль подсчёта осколков. Суть алгоритма подсчёта осколков изложена ниже.

Сплошное тело для расчёта динамических процессов, включая разделение на множество фрагментов, можно представить связным графом с вершинами в дискретных частицах. Каждая вершина графа — центр масс дискретной частицы (т. е. разностной ячейки). Линии, соединяющие вершины графа, — это связи частиц по признаку физической близости, т. е. эти частицы взаимодействуют между собой.

При деформировании тела происходит смещение дискретных частиц относительно друг друга. Увеличение расстояния между частицами приводит к разрушению физических связей, при этом возможна смена соседей и даже потеря части связей вплоть до разделения тела на отдельные осколки и крупные фрагменты.

Что такое осколок с точки зрения моделирования? Очевидно, что это выделившаяся в результате образования сквозных трещин некоторая часть частиц тела или часть счётной области.

Каждая частица в модели имеет свой номер, свои материальные и динамические характеристики. Требуется подсчитать частицы. С этой целью строятся списки соседей для каждой частицы. У каждой частицы будет свой список, причём его длина будет определять число связанных между собой частиц, т. е. количество частиц, находящихся в данном осколке.

Однако использование оптимального списка соседей, с точки зрения вычислений, приводит к значительным затратам машинного времени из-за большого числа переборов. Для существенного снижения времени вычислений соседей в осколках был построен список соседей с двухсторонними связями, что позволило описать полностью связный граф.

При обработке списков обращает на себя внимание то, что для любой связи « I → J » находится парная ей связь « J → I ». Таким образом, зная все связи для любой вершины графа, можно при пересчёте вершин последовательно выключать их из списка. Данная процедура на порядок снизила затраты времени на подсчёт числа вершин в осколках и, соответственно, самих осколков.

В качестве объекта исследования построена схематичная 2 D -модель КА. Параметры модели: длина приборного контейнера 1,8 м, диаметр порядка 1 м и масса ~2 500 кг.

Решение задачи в плоской 2 D постановке для заведомо трёхмерного объекта обосновывается следующими факторами.

Фактор первый — развитие программной реализации задач высокоскоростного удара мы ведём последовательно — «от простого к сложному». Так, например, в 1990-х гг. мы располагали программным средством расчёта высокоскоростного удара только в одномерной постановке (авторы Г.А. Сапожников, А.Е. Медведев, М.К. Лебедева, ИТПМ СО РАН). Однако, применив псевдотрёхмерную обработку результатов расчёта (М.Ю. Федоров) [8], смогли выполнить «оценку сверху» возможных последствий взаимодействия КМ с советскими космическими ЯЭУ. При таком подходе программа, реализующая задачу удара в 2 D постановке, имеет право на применение.

Фактор второй — потребность в оценке безопасности КА и советских космических ЯЭУ в части последствий столкновений с КМ зачастую превышает ресурсы времени разработчиков. В т. ч. всегда сказывалась и недостаточность финансирования.

Фактор третий — консервативный подход. В плоской постановке задачи мы получаем за счёт отсутствия разгрузки среды в направлении третьей координаты Z заведомо худший результат по степени разрушения объекта и количеству осколков, т. е. получаем «оценку сверху».

В настоящее время продолжается работа и по развитию комплекса для расчёта высокоскоростного взаимодействия сложных технических объектов в трёхмерной постановке. К настоящему времени основной этап этой сложной, но, несомненно, важной работы завершён, теперь потребуется обкатка на моделях сложной геометрии.

На рис. 4 показана модель гипотетического КА, которая включает в себя характерные конструктивные элементы: солнечные батареи (материал — кремний на тонком алюминиевом каркасе — рис. 5); антенну; бак рабочего тела для электроракетного двигателя и сам двигатель. Внутрь внешней оболочки помещена разветвлённая конструкция, имитирующая электронные приборы, установленные на панели системы отвода тепла, приборы обеспечения ориентации и стабилизации, приводы солнечных батарей, алюминиевые и стальные конструкции.

В качестве КМ выбран круглый объект («микроспутник») диаметром d = 200 мм с тонкостенной стальной оболочкой толщиной h = 2 мм. Параметры внутреннего содержимого приняты как для алюминия (плотность 2 710 кг/м³), исходя из соображений, что средняя плотность каталогизированного КМ [5], куда входят и выключенные КА, колеблется в пределах 2 500…3 900 кг/м³.

Рассматривается удар под углом с относительной скоростью W = 11,7 км/с. Разложение скорости удара по осям координат V_x = 8,27 км/с; V_y = 8,27 км/с.

Время счёта процесса до 940 мкс составило 192 ч на настольном компьютере Intel® Core™ i7-3820 CPU@ 3,60 GHz, оперативная память 32 Гб.

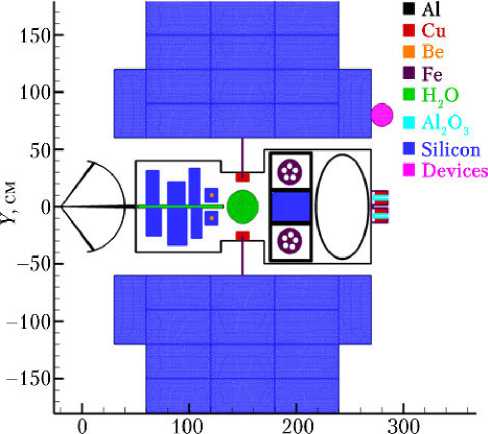
X, см

Рис. 4. Модель космического аппарата

■ Алюминий

О Кремний

1201                              ---------------

110 -

100 -

90'--

80 - ill.!

80         100         120         140

Рис. 5. Фрагмент солнечной батареи с расчётной сеткой

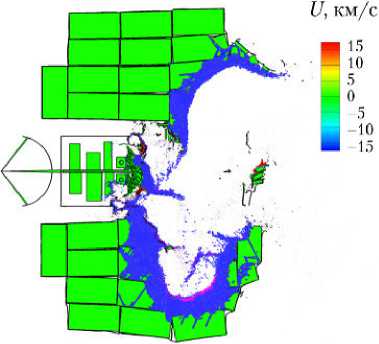
На рис. 6 приведены четыре фазы катастрофического разрушения спутника с образованием множества мелких осколков и отделением крупных фрагментов конструкции.

Значительная схематизация является методическим приёмом при моделировании сложной конструкции и определяется, как отмечалось выше, применением настольного компьютера для решения чрезвычайно ресурсоёмких задач.

При анализе результатов численного эксперимента, если потребуется, применяется «обратный ход», когда осколкам соответствующего размера ставятся в соответствие вполне определённые фрагменты конструкции, например, выполненные из материалов, представляющих опасность для окружающей среды.

Программа позволяет по временным шагам проследить процесс разрушения объекта. Разрушенная область модели без труда может быть поставлена в соответствие конкретной зоне (элементу) конструкции.

При ограниченном наборе основных материалов, образующих конструкцию, и при катастрофическом разрушении объекта химический состав осколков принимается в соответствии с объёмными долями веществ объекта [8].

Сценарий численного эксперимента, результаты которого будут обсуждаться ниже, заключается в воздействии стального ударника ∅1 см на модель выключенного реактора советской ЯЭУ «Бук» [7] при относительной скорости удара W = 11,7 км/с с разложением скорости в направлении X U = –8,27 км/с; в направлении Y V = –8,27 км/с (рис. 7).

Цель расчёта состоит в получении поля размеров и скоростей образовавшихся осколков. То есть, в отличие от модели КА (см. рис. 1) расчёт выполнялся с подключением программного модуля «осколки».

На рис. 8 приведена конечная фаза разрушения реактора и разлёт осколков.

На рис. 9–11 показаны гистограммы количества осколков, скорости осколков в продольном направлении X и в поперечном направлении Y в зависимости от размера, соответственно.

Гистограмма рис. 9 показывает, что основное количество осколков лежит в области мелких частиц размером до 0,5 см в поперечнике. В этом диапазоне находятся тысячи частиц, в то время как количество осколков размером 2 см и больше исчисляется единицами и десятками. Сдвиг гистограммы в отрицательную область размеров — результат некорректной передачи изображения программой-визуализатором. При выводе на экран с многократным увеличением области гистограммы вблизи нуля этот эффект исчезает, но картинка становится неудобной для восприятия.

В табл. 1 и 2 приведена расшифровка данных гистограмм по количеству и скоростям осколков, соответственно.

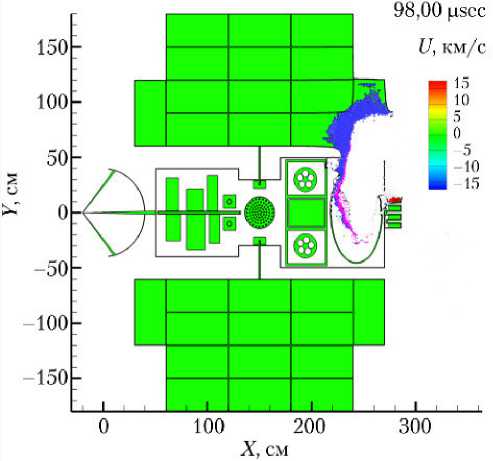
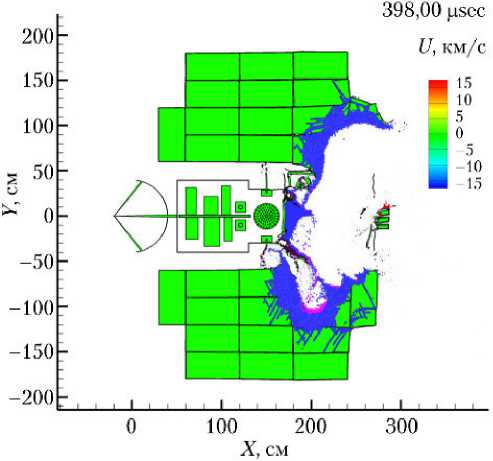
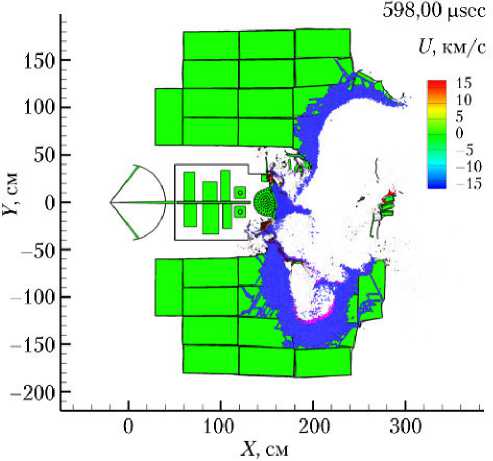
Рис. 6. Четыре фазы разрушения модели КА

В 0

-100

-200

880,00 цзсс

, 1 1 1 1 . 1 ; 1 1 . 1 . . 1 . 1 1 . I_____________I______L 0      100     200     300     400

X, см

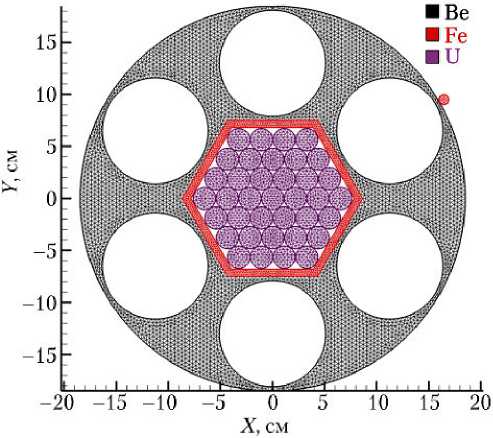
Рис. 7. Расчётная модель реактора

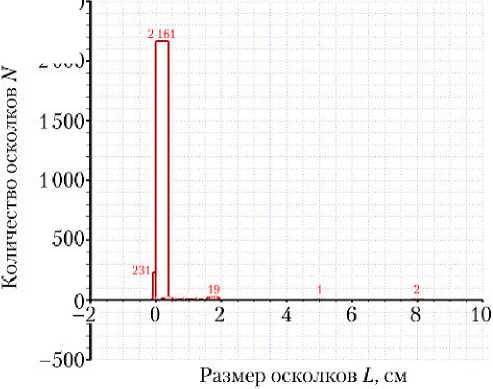
Рис. 9. Гистограмма количества осколков в зависимости

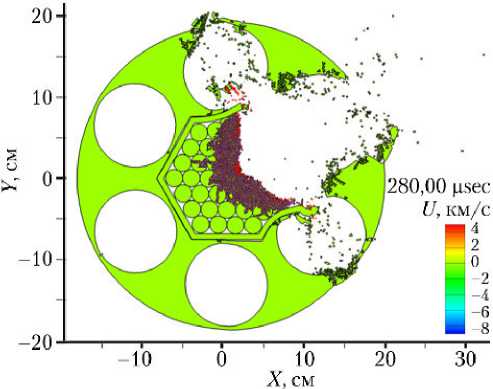
Рис. 8. Конечная фаза разрушения реактора и разлёт осколков

от поперечного размера

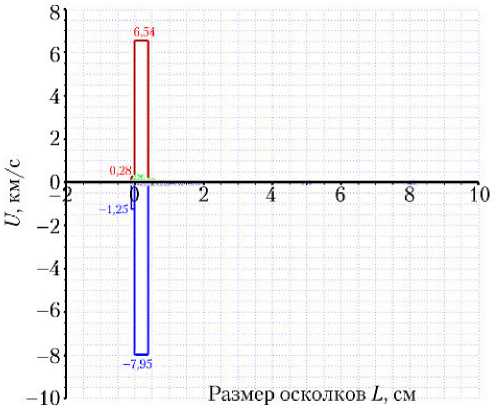
Рис. 10. Гистограмма скоростей осколков в продольном направлении X

Таблица 1

количество осколков N в зависимости от диапазона размеров d , мм

d , мм	0,1–0,5	0,5–1,0	1,0–2,0	3,0–4,0	5,5–6,5	8,0–9,0	12,0–13,0	17,0–18,0	49,0–51,0	80,0
N	5	231	2 161	15	3	5	5	19	1	2

Таблица 2

Скорости осколков (в продольном направлении — U , км/с, в поперечном направлении — V , км/с) в зависимости от размера d , мм

d , мм	0,1–0,5	0,5–1,0	1,0–2,0	3,0–4,0	5,5–6,5	8,0–9,0	12,0–13,0	17,0–18,0	49,0–51,0	80,0
+U	0,01	0,01	6,51	0,09	0,01	0	0	0	0	0
–U	0,03	0,03	7,96	0,05	0,01	0	0	0	0	0
+V	0,04	0,79	7,10	0,08	0,01	0,05	0,01	0	0,001	0,01
–V	0,02	0,99	7,40	0,09	0,01	0	0,02	0,01	0	0,003

Примечание. «0» — скорость менее 1 м/с.

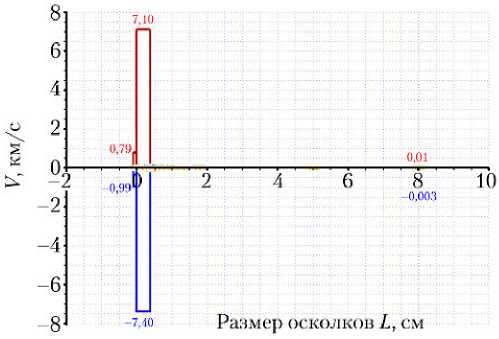
Рис. 11. Гистограмма скоростей осколков в поперечном направлении Y

Как отмечалось выше, важным аспектом при разработке программного средства, предназначенного для численного моделирования быстропротека-ющих физических процессов, является его верификация и сопоставление результатов с данными экспериментов. На протяжении всего срока разработки программных модулей комплекса REACTOR этой работе уделялось достаточное внимание. Например, в диссертационной работе Крауса Е. И. [23] сравнение результатов теоретических разработок по уравнению состояния проводилось с данными экспериментов и результатами других авторов (Альту-шер, Молодец, Бушман, Кормер и др.). Проводилось также сравнение данных расчётов по ударному взаимодействию тонкой пластинки с деформируемой преградой и экспериментальных данных из работы [24].

Результаты численного моделирования взаимодействия монолитных и гетерогенных преград с деформируемыми ударниками с оживальной формой головной части [25] сравнивались с экспериментальными данными работы [26].

Моделирование пробивания разнесённых пластин сферическим ударником [27] сопоставлялось с данными работы [28].

Во всех случаях получено хорошее согласование результатов расчётов при применении комплекса REACTOR с данными соответствующих экспериментов.

выводы

Проблема техногенного засорения околоземного космического пространства определяет актуальность работ по моделированию последствий высокоскоростных ударных воздействий на КА, в т. ч. советские КА с ЯЭУ «Топаз» и автономно существующие на орбитах захоронения ЯЭУ «Бук».

Разработанный комплекс программ REACTOR позволяет исследовать процессы ударного разрушения сложных технических объектов в 2 D постановке в широком диапазоне скоростей взаимодействия.

При решении задач на разветвлённых конструкциях для получения конечного результата в разумные промежутки времени требуется схематизация модели. Для перехода к натурному объекту при анализе полученных результатов численного эксперимента применяется «обратный ход», когда фрагменты разрушенного объекта отождествляются с соответствующими элементами конструкции, например, если эти элементы выполнены из материалов, содержащих радиоактивные или токсичные вещества.

Численное решение в комплексе REACTOR может быть доведено до «конца», т. е. до исчерпания запасов кинетической энергии налетающего тела и, что важно, с определением спектра образовавшихся осколков для последующей оценки рисков для окружающей космической среды и среды обитания человека.