Численное моделирование высотомера малых высот с двойной частотной модуляцией

DOI:

Высотомеры малых высот, построенные по схеме измерения биений сигналов с частотной модуляцией зондирующего и отраженного (ЧМ-высотомеры), отличаются простотой технической реализации, однако обладают существенным недостатком — так называемой «дискретной ошибкой», определяемой девиацией частоты Аш и носящей методический характер [1]. Одним из наиболее простых средств подавления дискретной ошибки является использование дополнительной «медленной» модуляции средней частоты сигнала. Достоинством такого метода является простота технической реализации, выражающаяся в минимальной доработке СВЧ-тракта и регистрирующего устройства, которое должно работать в режиме усредняющего счета. Работы в этой области [2; 3; 5] опираются на вполне конкретный вид закона «медленной» модуляции (пилообразный или гармонический). Такой подход достаточно нагляден, приводит к легко реализуемым результатам, однако оставляет открытым вопрос о потенциальных возможностях снижения дискретной ошибки указанным методом в рамках технических ограничений на девиацию частоты и время измерения.

На рисунке 1 представлена структурная схема ЧМ-высотомера малых высот. При отражении сигнала ж 1 (t) = Л 1 cos \Ф (t)] от поверхности, до которой измеряется расстояние, в приемник поступает сигнал с задержкой фазы на величину т = 2^ : ж ₂ (t) = = Л ₂ cos \Ф (t — т)].

Сигнал с выхода фильтра нижних частот (ФНЧ) поступает на ограничитель и далее — на счетчик. С учетом малости величины задержки τ (для высот до 100 м она составляет ^ 10 ^-7 с) сигнал на выходе фильтра можно записать в виде:

г (t) = Л cos \Ф (t) — Ф (t — т)] « Л cos \ш (t) т].

В стандартном ЧМ-высотомере циклическая частота со временем изменяется по гармоническому закону ш (t) = ш ₀ + Аш cos fit [1], что приводит к записи:

г (t) = Л cos \ш^ + Ашт cos fit],

где ш ₀ — несущая частота сигнала; Аш — девиация частоты; fi — модулирующая частота (fi ^ Аш, ш ₀ ). Усредняющий счетчик измеряет количество положительных переходов через нуль сигнала (2) на некотором временном интервале. При этом показания счетчика за период модуляции Т = 2п изменяются на величину:

N =

— (/ о + А/) с

-

— (/ о с

-

А/) ,

где L x J — целая часть числа х. Зависимость показаний N счетчика от высоты R (рабочая характеристика высотомера) для несущей частоты / 0 = ^ 0 = 450 МГц и девиации А/ = 4^ = 25 МГц приведена на рисунке 2.

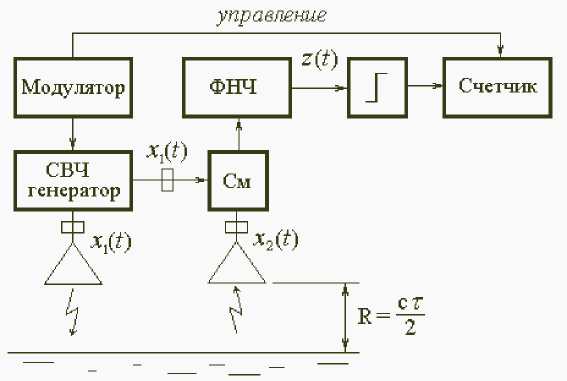
Рис. 1. Блок-схема ЧМ-высотомера малых высот

Эта зависимость немонотонна и, следовательно, обратная зависимость R (N ), по которой можно определить расстояние, неоднозначна в пределах AR = О^П , что и составляет «дискретную ошибку» ЧМ-высотомера. Среднеквадратическое отклонение o r зависимости N (R) от линейной составляет 1,217 м, однако в ряде задач (например, при измерении уровня нефти в танкерах, автоматической посадке и т. п.) требуется большая точность [4; 6].

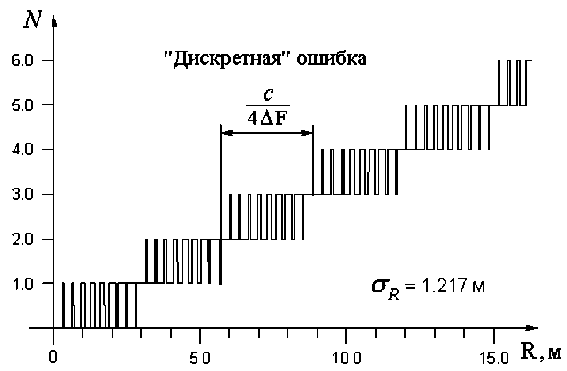
Рис. 2. Рабочая характеристика ЧМ-высотомера

• 1.    Подавление «дискретной ошибки» с использованием дополнительной частотной модуляции

Наиболее простым способом повышения точности ЧМ-высотомера является введение дополнительной «медленной» модуляции частоты несущей в каждом периоде Т и усреднении результатов счета. При этом

N (F _k ) =

^(/ 0 + △ / + ^F k )

С

-- ^(/ 0 - △ ^/ + ^F k )

С

где F k = F (кТ ) — значение медленной модуляции F (t) в к-м периоде. Усреднение показаний происходит за время Т _т = МТ (М периодов):

л м

N^ = М ^N (Fk), k=1

что позволяет счетчику работать в режиме непрерывного счета в течение времени t Е Е (0,Т т ).

Простейшей формой дополнительной частотной модуляции F (t) является линейная: F (t) = 2 Т^4 ; t Е [— Т Т ; Т т] . При такой форме и усредняющем счете за М = 200 периодов частоты модуляции Q рабочая характеристика высотомера N ^ (R) в пределах 3-15 м имеет среднеквадратическое отклонение от прямой o r = 0,121 м (рис. 3).

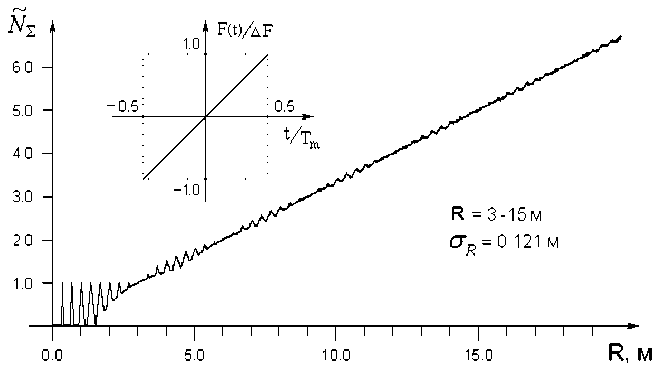
Рис. 3. Рабочая характеристика высотомера при линейной дополнительной частотной модуляции. Девиации частоты основной и дополнительной модуляции выбраны одинаковыми ( А/ = AF = 25 МГц)

Начальный участок характеристики (R < 3 м), не поддающийся подавлению дис- кретной ошибки, можно исключить при начальной установке высотомера.

Однако линейная форма модуляции не является максимально эффективной. Так, например, при использовании нелинейной формы дополнительной модуляции вида F (t) =

2^ arcsin П          Т_т J

при тех же значениях полосы частот линейность рабочей характе- ристики дальномера значительно выше: среднеквадратическое отклонение зависимости ̃︁

N ^ (R) от линейной в диапазоне дальности 3-15 м составляет o _r = 0, 046 м (рис. 4).

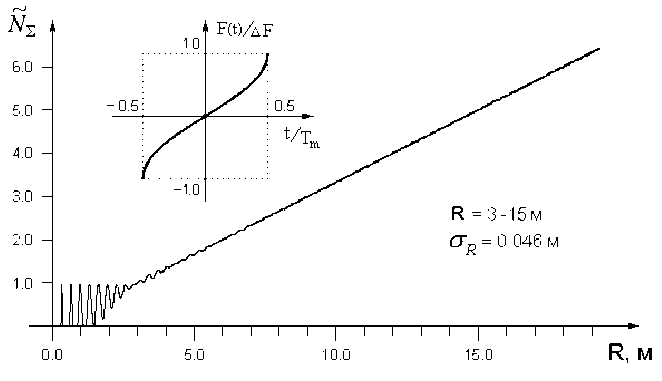
Рис. 4. Усредненные показания счетчика ЧМ-высотомера с двойной частотной модуляцией:

f o = 450 МГц, А/ = AF = 25 МГц, F (t) = ^2V' arcsin (^

В процессе моделирования использовался также параметрический закон изменения дополнительной частотной модуляции:

F ( a ,t) = |a (t) x (1

-

-

α

- [1 — a (t) x (1

^m /                \

-

1     2t

/ m

a )} AF.   (5)

Модельные расчеты показывают, что при значении параметра a = 0, 62 в выражении (5) и приведенных выше частотных параметрах / 0 и AF среднеквадратическое отклонение рабочей характеристики от линейной в диапазоне дальности 3-15 м составляет а д = = 0,043м.

Заключение

Таким образом, использование дополнительной частотной модуляции в высотомерах малых высот позволяет значительно (не менее чем на порядок) повысить точность измерения расстояния. При этом потенциальные возможности повышения точности определяются диапазоном рабочих дальностей и формой дополнительной «медленной» модуляции.

Использование сложных видов «медленной» модуляции с добавлением положительной третьей производной и оптимизация в заданном диапазоне высот позволяет дополнительно в 2–3 раза снизить среднюю погрешность измерения относительно линейной формы модуляции, без расширения занимаемой полосы частот. При этом реализация сложных видов модуляции на низкой частоте повторения ( ^ 5 — 20 Гц) не составляет трудностей при использовании средств бортовой компьютерной техники.