Численное моделирование взаимодействия бризерных решений (2 + 1)-мерной 𝑂(3) нелинейной сигма-модели
Автор: Шокиров Фарход Шамсидинович
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Физика и астрономия
Статья в выпуске: 4 (47), 2018 года.
Бесплатный доступ
Методами численного моделирования проведено исследование процессов взаимодействия бризерных решений в фазовом пространстве (2 + 1)-мерной суперсимметричной 𝑂(3) нелинейной сигма-модели. Получены модели лобовых столкновений, где в зависимости от динамических параметров системы наблюдаются процессы объединения бризеров, образования связанных состояний (сдвоенных бризеров), столкновения и отражения, прохождения бризеров друг сквозь друга, а также их разрушения. Показано, что бризеры 𝑂(3) нелинейной сигма-модели при взаимодействии более устойчивы относительно аналогичных решений уравнения синус-Гордона. При наличии ротационной изоспиновой динамики система бризерных полей после столкновения излучая определенную часть энергии, сохраняет структурную устойчивость с характерной периодической осцилляцией. Выявлены свойства продольно-поперечных колебаний сдвоенных бризеров и скачкообразного увеличения скорости бризеров, отражающихся друг от друга после взаимодействия. Численные модели построены на основе методов теории конечных разностных схем c использованием свойств стереографической проекции, с учетом теоретико-групповых особенностей конструкций класса 𝑂(𝑁) нелинейных сигма-моделей теории поля. Разработан комплексный программный модуль, реализующий алгоритм численного расчета.
Нелинейная сигма-модель, разностная схема, стереографическая проекция, сфера блоха, усредненный лагранжиан, уравнение синус-гордона
Короткий адрес: https://sciup.org/149129849
IDR: 149129849 | УДК: 519.6:530.1 | DOI: 10.15688/mpcm.jvolsu.2018.4.6
Текст научной статьи Численное моделирование взаимодействия бризерных решений (2 + 1)-мерной 𝑂(3) нелинейной сигма-модели
DOI:
Исследование процессов формирования, эволюции и взаимодействия пространственно-однородных колебательных мод, которые можно интерпретировать как классические модели составных частиц (например, поле мезонов), является нетривиальной задачей в солитонной теории [1; 2; 4; 6; 11; 13; 16; 19–21; 23; 26]. Особым классом практических задач в данной теории является поиск и исследование свойств локализованных когерентных структур, обладающих собственной динамикой внутренней степени свободы — так называемых пузырей, пульсонов, бионов [1; 2; 6; 19; 20], бризеров, световых пуль [4; 11; 13; 16; 21; 23; 26]. В работе [14] был предложен один из вариантов асимптотического решения данной задачи в рамках (2 + 1) -мерной 0(3) нелинейной сигма-модели (НСМ). В настоящей работе на основе результатов, полученных в работе [14] (см. также [25]), проведением численных расчетов построены модели, описывающие процессы взаимодействия бризерных решений (2 + 1) -мерной 0(3) НСМ. Моделирование процессов взаимодействия данных решений проведено с целью более подробного изучения их реальной динамики [6] и структурной устойчивости. Полученные в работе [14] двумерные осциллирующие решения сохраняют устойчивость в течение достаточно долгого времени численного моделирования ( t G [0; 270] ), где потеря энергии на излучение составляет: Еп га( } < 5,15 % . Заметим, что численные исследования осциллирующих решений теоретико-полевых моделей с использованием вычислительных процессоров имеют более чем полувековую историю (см., например, [1; 2; 6; 19; 20] и указанную в них литературу). В частности, в работах [1; 2] были обнаружены и исследованы метастабильные (с временем жизни порядка 10 3 периодов осцилляций) пульсирующие солитоны, так называемые пульсоны уравнения синус-Гордона (УСГ) в сферическом трехмерном пространстве. Подробное исследование процессов взаимодействия цилиндрически-симметричных пульсонов и так называемых Q -солитонов проведено в работах [6; 19; 20]. В частности, в указанных работах построены модели лобовых столкновений пульсонов и обнаружено, что при взаимодействии время жизни пульсонов остается таким же, как и в свободном состоянии. Также было показано, что существуют некоторые критические величины v cr скорости движения взаимодействующих пульсонов, определяющие процесс образования их связанных состояний (v < v CT ) или выхода из взаимодействия (v > v CT ) с последующим их разрушением [6; 19].
В настоящей работе проведением экспериментов, аналогичных вышеуказанным для бризерных решений 0(3) НСМ, полученных в работе [14], показано, что данные решения являются более устойчивыми как в свободном состоянии, так и при их взаимодействии.
Плотность функции Лагранжа и гамильтониан исследуемой 0(3 ) НСМ в стандартной (изоспиновой) параметризации можно записать в следующем виде (см., например, работы [3; 5; 9; 10; 15; 17; 18; 22]):
L = ^[9^9 ^ S a - (1 - S 2 )], (1)
Н = 2[(d o S a ) 2 + (d i S a ) 2 + (d 2 S a ) 2 + 1 — s 3 ] , (2)
где S(s1,s2, S3) = S(sin 0 cos (p, sin 0 sin cp, cos 0) единичный вектор — триплет реальных скалярных полей, удовлетворяющих условию S2 = 1; 9Ц9ц = дгк9W9W = 9t9t — 9Х9Х — 9У9У (^ = 0,1, 2; a = 1, 2, 3); дгк — метрический тензор (г, к = 1, 2, 3). Первое слагаемое в (1) является известным выражением функции Лагранжа НСМ в изотропном случае [3; 5; 9; 10; 15; 17; 18; 22; 25]. Исследование настоящей работы проведено в рамках анизотропной 0(3) НСМ, где анизотропия выбрана в направлении s3-компоненты. Симметрией модели является 0(3) — симметрия динамики изотопического вектора (изовектора) в блоховской сфере S2 = SU(2)/U(1) = 5*0(3)/S0(2). Таким образом, состояние исследуемой НСМ описывается движением точки на единичной двумерной сфере S С R3, эквивалентным движению конца изовектора S. Лагранжиан анизотропной 0(3) НСМ использован как в изоспиновой параметризации (1), так и в эквивалентных эйлеровой
L = |[дц0д-0 + sin 2 0(Эцфд-ф — 1)], (3)
и комплексной параметризациях
9 ^, 59 - г — 5 г = 2 (1 + 5г) 2
где 0 = 0(t) G [0; 2п] и ф = ф(t) G [0,2п] — эйлеровы углы; г = ж + гу, 5 = ж — — гу. Соотношения между вышеуказанными параметризациями определяются на основе применения свойств стереографической проекции сферы S2 на комплексную плоскость г = ж + гу = 51 + г82 = eiф tg 0. (5)
1 ± S 3 2
Необходимость перехода на комплексную параметризацию состоит в численном подходе. Проблема заключается в том, что бесконечно большие величины, возникающие на полюсах блоховской сферы S 2 в обычной стереографической проекции, приводят к ошибке в машинном счете вследствие появления операции деления на ноль. Для преодоления данной проблемы в работе [10] была предложена идея проецирования точек нижней части сферы ( s 3 < 0 ) на нижнюю комплексную плоскость, соответственно точек верхней полусферы ( s 3 > 0 ) на дополнительную, верхнюю комплексную плоскость. Таким образом, при эволюции вектора изотопического спина на верхней/нижней части сферы расчеты проведены в верхней/нижней комплексной плоскости. Далее по «экватору» ( s 3 = 0 ) специальным образом проводится «сшивка». В итоге получим параметризацию 0(3) НСМ в комплексном виде (4).
Соответствующие уравнения Лагранжа — Эйлера для 0(3) НСМ (1), (3) и (4) принимают следующий вид:
9-9^Si + Si^Sad-Sa?) — Sy(5iy - Si Sy) = 0,
(1 + 5г )9-9-г — 259^59-г + г(1 — 5г) = 0,
2d^d-0 + sin(20)(1 — 9-ф9-ф) = 0,
2 cos 0дц,фд-ф + sin 0д^д-ф = 0, где 5iY — символ Кронекера, - = 0,1, 2; г = 1, 2, 3; SiSi = 1; у = 3; г = ж + гу, 5 = ж — гу. Разностные схемы для численного моделирования составлены для уравнения (6.2). Значения плотности энергии бризерных полей определяются выражением (2) с учетом соотношений (5). Заметим, что 0(3) НСМ в частном случае сводится [3; 5; 10; 15; 17; 18; 22] к вполне интегрируемому уравнению синус-Гордона (УСГ). В случае уравнений (6.3)
движение изовектора S ограничивается меридианным сечением — ф = 0 , 0 6 [0; 2п] (рис. 1 а ) пространства сферы S 2 и с учетом (5) описывается УСГ следующего вида:
0 tt - 0 хх - 0 уу + ^ sin(2 0 ) — 0.
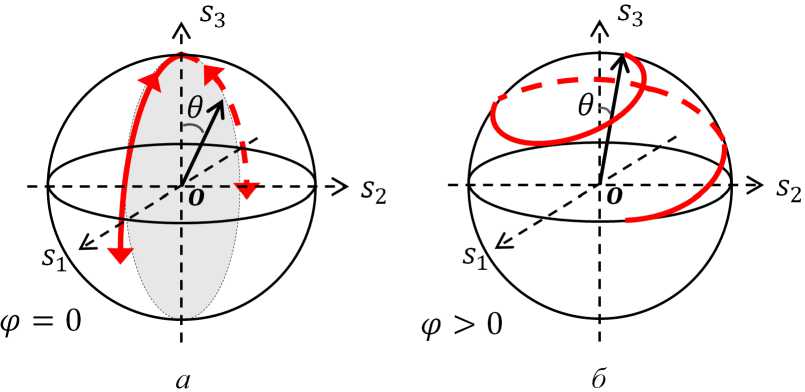
Рис. 1. Динамика S ( s 1 ,s 2 , S 3 ) в пространстве сферы S 2 : а - ф = 0; б - ф > 0
В численных экспериментах настоящей работы использованы приближенные решения осциллирующего типа, найденные в работе [14] методом усреднения лагранжиана (2 + 1) -мерного УСГ следующего вида:
U tt - и хх - и уу + sin и — 0. (8)
Исследования, проведенные в работе [14], были мотивированы результатами работы [21], где в гамильтоновом подходе на основе пробной функции вида
u(ж,y,t) — — 4arctg[A(t)(1 — Л(t) 2 ) -1/2 sin v(t) ch -1 (Лж) ch -1 (Лу)] (9)
были получены относительно устойчивые решения УСГ (8), названные в указанной работе бризерами. В работе [14] выражение для усредненного лагранжиана УСГ (8)
L — 2 (u 2 — u X — U y ) — 1 + cos и относительно быстрой фазы v(t) получено в следующем виде:
L — 2A t 2 (1 — Л 2 ) -3/2 + (1 — Л 2 ) -1 / 2 4Л 2 v 2 — 16(3Л -1 th -1 Л — 2). (10)
Выражение (10) зависит только от фазовых переменных Л(t) и v(t) , которые являются основными параметрами, определяющими динамику пробной функции (9) [21]. В работе [14] из уравнения Лагранжа — Эйлера для (10) были получены выражения для Л(t) и v(t) . Полученное бризерное решение вида (9) в изоспиновой параметризации 8 ^ ( г — 1, 2, 3 ) принимает следующий вид:
8 1 — — 2^/(1 + ^ 2 ) cos ф, 8 2 — — 2^/(1 + У 2 ) sin ф, 8 3 — (1 — ^ 2 )/(1 + £ 2 ), (11)
^(ж, y, t) — Л(1 — Л 2 ) -1/2 sin v ch -1 (Лж) ch -1 (Лу).
В работе [14] на основе найденных параметров A(t) и v(t) были построены численные модели неподвижных и движущихся решений вида (9) УСГ (7) в рамках 0(3) НСМ (при ф = 0 в (11)). В частности, было показано, что найденные решения сохраняют устойчивость в течение достаточно долгого времени — t < 270 . В случае неподвижных (v (^ o ) = 0 ) бризеров для t Е [0; 270] (45 000 итерационных циклов) потеря энергии ( En loss) [20] бризерного поля не превышала 5,15 % [14], где
En i oss = En(t o ) - En(t),
En(t) = У EI(x,y,t)dxdy.
Далее в работе [14] с учетом (7), добавлением возмущений трехкомпонентному изовектору
Л3
-поля
S
(s
1
,s
2
,s
3
)
в пространстве сферы
S
2
Е
R3
(см. рис. 1
б
) [7; 9] построены решения для
0(3)
НСМ (1). Показана устойчивость построенных решений в стационарном и движущемся состояниях в течение достаточно долгого времени (
t
<
<
270
), при этом бризеры
0(3)
НСМ (1) оказались более стабильными
(
En
loss
<
4, 8 %
, для (to + т) = o) + 0, 5т, при v(to) = 0) по отношению к аналогичным решениям УСГ (7).
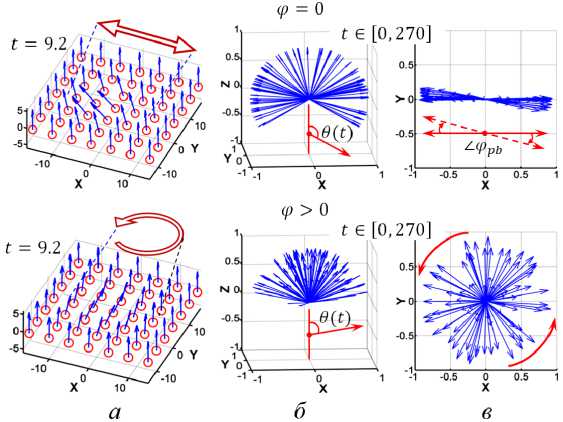
1. Численная модель двумерного бризера В настоящей работе использован подход приближения разностных схем [12], а также алгоритм и численная схема, которые были предложены в работе [10] для неподвижного локализованного решения (см. также [9]). Использована трехслойная разностная схема второго порядка точности 0(т2+ h2) на пятиточечном шаблоне с весами явного типа [12]. Аппроксимация проведена на прямоугольной сетке L(x,y): 4 400 х 2 200, где hx = hy — шаг сетки по координате, т — по времени. Устойчивость разностной схемы удовлетворяет требованиям для гиперболических систем уравнений: т/h < 1. На рисунке 2 приведена иллюстрация распределения плотности энергии (2) (DH, Density of Hamiltonian) и ее контурной проекции [25] для случая v(t0) = 0, t0= 0, а также динамика центральной точки DH(0, 0, t) (11) при t Е [0; 270]. Наличие дополнительного вращения, заданного изовектору S при t0+ т (ф(t0+ т) = ф(to) + шт, ш = 0) в пространстве сферы S2[25] (рис. 1 б), приводит к формированию бризерного решения 0(3) НСМ (бризер с вращением изотопических спинов). При этом наблюдается увеличение площади DH (рис. 2б), определенная диссипация динамики внутренней степени свободы, а также увеличение значения интеграла энергии (En) бризерного поля [14; 25]. В экспериментах работы [14] в случае ф = 0 (рис. 3а,б) наблюдаются некоторые отклонения движения S от плоской (см. рис. 1а) траектории (рис. 3в). В данном случае возмущения фрь > 0 вызваны воздействием линейных волн, отражающихся от границ области моделирования: L[3001 х 3001]. По периметру L действуют специальные граничные условия [7; 9], которые поглощают линейные волны возмущений, излучаемые формирующимся бризером [10; 25]. Тем не менее при относительно интенсивном излучении определенная часть линейных волн, отражаясь от границ L, вносит некоторые возмущения фрь = 0 в динамику бризерного поля (11). На рисунке 3 угол 0(t) определяет отклонение вектора изоспина от оси 0Z, а ф(t) — ротационную динамику вокруг этой оси [9; 14] (см. рис. 1 б, 3в). Рис. 2. Плотность энергии, ее контурная проекция и динамика центральной точки DH(0,0,t) стационарных бризеров вида (11) модели (1): а — p(t) = 0, tin = 15,8; б — p(t) > 0 (ш = 0,5), tin = 16,8. Общее время моделирования: t Е [0; 270] НСМ обладают формальной лоренц-инвариантностью [3; 15], позволяющей провести в ее рамках исследование нелинейных свойств локализованных решений и динамику их взаимодействия [24]. Рис. 3. Изоспиновая структура неподвижных бризеров (11) модели (1) при p(t) = 0 (вверху) и p(t) > 0 (ш = 0, 5) (внизу): а — трехмерная иллюстрация при t = 9, 2 (в разряженном виде); б — движение изовектора S(si, 82,83) в точке 0(0,0,0); в - проекция S(s1, s2,s3) на плоскость (ж, у). Общее время моделирования: t Е [0; 270]
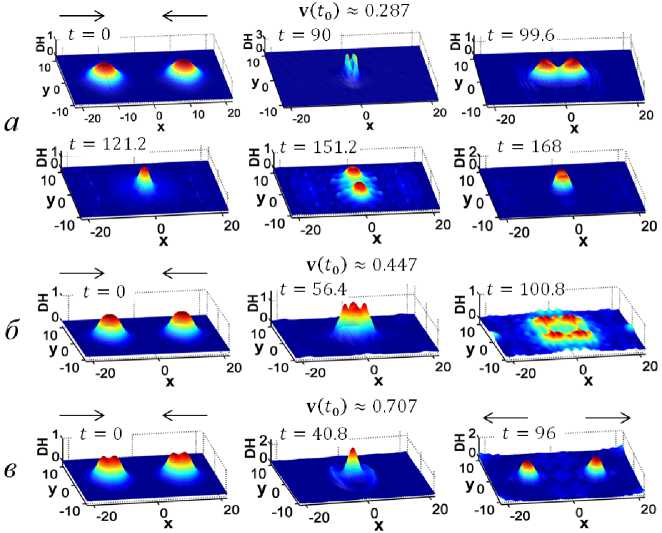
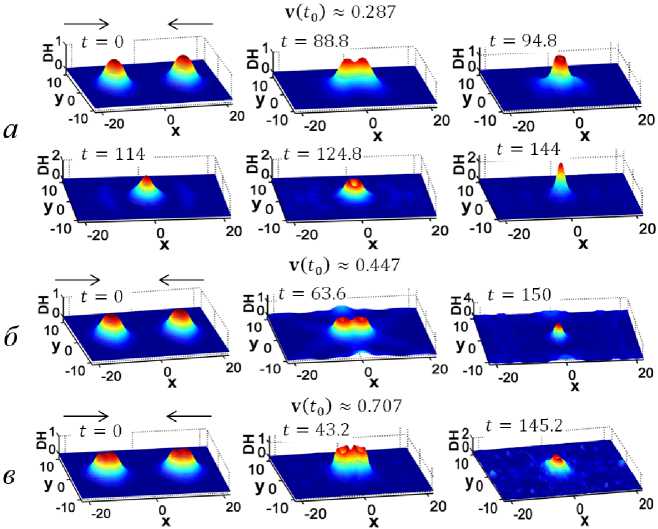
2. Взаимодействие бризеров УСГ На первом этапе рассмотрим модели лобовых столкновений [24] бризеров (11) в рамках УСГ (7) при различных значениях скорости их движения (рис. 4), где 81 = -2^/(1 + ^2), 82 =0, S3 = (1 - ^2)/(1 + ^2), (12) ^(x,y,t) = Л(1 — Л2) 1/2sin v ch 1(Лж)еН 1(Лу). В данном случае в зависимости от значения скорости движения сталкивающихся бризеров наблюдается три вида эволюции системы: |v(t0)| < 0,38 — объединение бризеров; |v(^o)| £ (0, 39; 0, 61) — разрушение бризеров; |v(t0)| > 0, 63 — прохождение бризеров друг сквозь друга. Скорость движения бризеров указана в долях скорости света (в вакууме): с = 1. Рис. 4. Плотность энергии процесса столкновения бризеров (11) УСГ (7) с заданной начальной скоростью (t0 = 0, ш = 0): а — v(to) « ±0, 287; б — v(to) « ±0,447; в — v(to) « ±0, 707. Общее время моделирования: t £ [0; 168] Объединение бризеров (v(t0) ~ ±0, 287). Бризеры при столкновении объединяются в единое устойчивое осциллирующее возмущение поля (рис. 4а). Потеря энергии системы взаимодействующих бризеров на излучение составляет Enloss ~ 4, 33 %. Особым свойством данной серии экспериментов являются периодические колебания составляющих осциллирующего возмущения строго в продольном и поперечном направлениях (см., например, рис. 4а: t = 99, 6, t = 151, 2). Разрушение бризеров (v(t0) ~ ±0,447). Бризеры при столкновении образуют локализованное осциллирующее возмущение, которое постепенно разрушается периодическим излучением энергии (рис. 4б). Прохождение бризеров друг сквозь друга (v(t0) ~ ±0,707). В отличие от предыдущих экспериментов в этом случае сталкивающиеся бризеры проходят друга сквозь друга (рис. 4в), хотя и при наличии излучения определенной части их энергии в виде линейных волн возмущений: Enloss ~ 16,48 %.
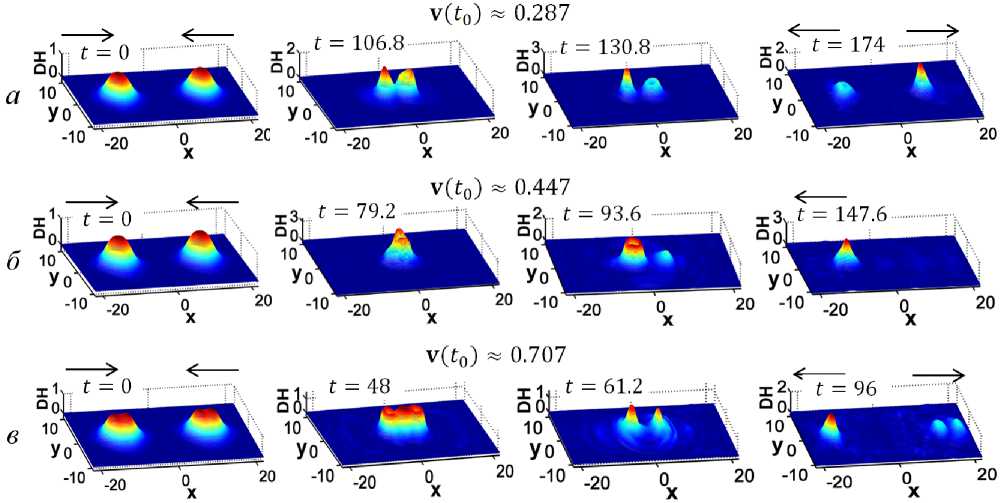
3. Взаимодействие бризеров 0(3) НСМ Столкновение бризеров при шrгght = wieft. В случае столкновения бризеров (11) 0(3) НСМ (1) с одинаковыми значениями ш, при всех значениях скорости их движения наблюдается объединение бризеров в единое осциллирующее возмущение. На рисунке 5 приведены результаты данной серии экспериментов при различных значениях v(t0) и ш = 0, 5, где Enioss = 8, 08 % (а), Enioss = 10, 64 % (б), Enioss = 19,45 % (в). Рис. 5. Плотность энергии процесса столкновения бризеров (11) 0(3) НСМ (1) с заданной начальной скоростью (t0 = 0, ф^0+ т) = ф(^) ± 0, 5т): а — v(to) « ±0, 287; б — v(t0) « ±0,447; в — v(t0) « ±0, 707. Общее время моделирования: t Е [0; 150] Столкновение бризеров при wTight = -ш1е^. Аналогично предыдущему пункту рассмотрены модели лобовых столкновений бризеров (11) 0(3) НСМ (1), но при значениях ш, описывающих взаимно обратные направления вращения вектора Л3-поля (рис. 6). В этой серии экспериментов наблюдается два варианта эволюции: отражение бризеров друг от друга (при |v(t0) < 0,411) и разрушение одного из бризеров (при |v(t0) > 0,42|). Столкновение и отражение (v(t0) ~ ±0,287). На рисунке 6а приведены результаты экспериментов, где бризеры после столкновения отражаются друг от друга. Потеря энергии системы на излучение составляет Enloss = 7,81 %. Наблюдается внезапное увеличение скорости движения бризеров. Разрушение бризера с шle/t < 0. На рисунках 6б и 6в приведены результаты для v(t0) ~ ±0,447 и v(t0) ~ ±0, 707 соответственно. Во всех экспериментах данной серии при столкновении наблюдается разрушение бризера, движущегося в обратном направлении по ж. Рис. 6. Плотность энергии процесса столкновения бризеров (11) 0(3) НСМ (1) с заданной начальной скоростью движения (to = 0, ^„ght(to + т) = ^(to) + 0, 5т, ^iejt(to + т) = ^(to) - 0, 5т): а — v(to) « ±0, 287; б — v(to) « ±0,447; в — v(to) « ±0, 707. Общее время моделирования: t Е [0; 174] В данном случае возможно два варианта эволюции системы — столкновение и отражение бризеров или их прохождение друг сквозь друга. К сожалению, численные модели настоящей работы не позволяют ответить точно на данный вопрос. Потеря энергии систем на излучение составляют соответственно Enloss = 44, 82 % и Enloss = 42,85 %.
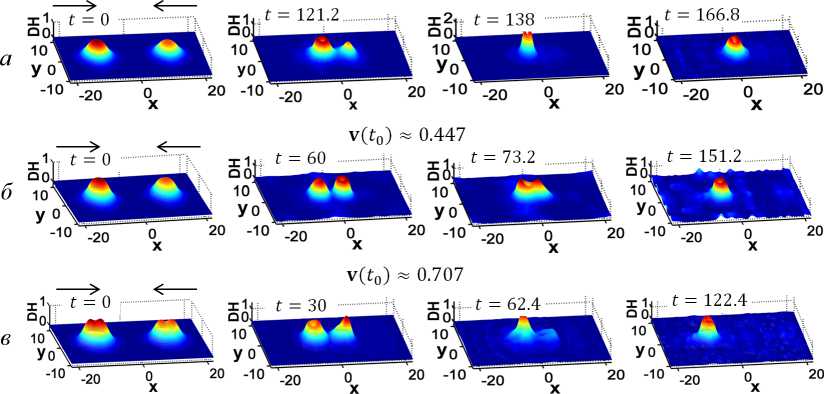
4. Взаимодействие бризеров 0(3) НСМ и УСГ В этой части работы приведены результаты экспериментов по столкновению бри-зеров (11) 0(3) НСМ (движущихся в положительном направлении оси ж) и бризеров (12) УСГ (движущихся в отрицательном направлении оси ж), обладающих значениями частоты вращения вектора А3-поля unsm = 0, 5 и w,sge = 0 соответственно. Во всех экспериментах данной серии наблюдается процесс разрушения бризерного поля УСГ, который происходит особым образом (рис. 7). На первом этапе при приближении друг к другу в резонансной зоне наблюдается притягивание («поглощение») бризерным полем 0(3) НСМ бризерного поля УСГ. Далее «объединенный» бризер периодически излучает часть энергии в виде радиальносимметричных линейных волн. Для моделей, приведенных на рисунке 7, величина излучаемой энергии имеет следующие значения: а — Enloss = 17, 56 %; б — Enloss = 20,4 %; в — Enioss = 31, 34 %.
5. Обсуждение полученных результатов Статические свойства солитонных решений в большинстве случаев поддаются аналитическому исследованию, но процессы их взаимодействия удается исследовать лишь численными методами, особенно в случае осциллирующих солитонов [6]. В настоящей работе построением численных моделей фронтальных столкновений бризерных решений осуществлена попытка исследования динамики их взаимодействия. Все солитонные решения, использованные при построении моделей, были получены асимптотическими методами в работах [14; 25]. v(t0) ~ 0.287 Рис. 7. Плотность энергии процесса столкновения бризеров (11) 0(3) НСМ (1) с заданной начальной скоростью (t0 = 0, v„ght(t0 + т) = ф(t0) + 0, 5т, фи/t(t0 + т) = 0): а — v(to) и ±0, 287; б — v(to) и ±0,447; в — v(to) и ±0, 707. Общее время моделирования: t Е [0; 166, 8] Результаты первой группы экспериментов по лобовому столкновению бризерных решений УСГ (в рамках 0(3) НСМ при ф(7) = 0) приведены во второй части работы. Известно, что движущиеся солитоны вполне интегрируемого УСГ проходят друг сквозь друга с сохранением формы и энергии, приобретая лишь фазовый сдвиг. Однако в экспериментах, описанных на рисунке 4, столкновение бризерных солитонов УСГ при скоростях их движения в пределах |v(t0)| < 0,63 не являются упругими (рис. 4а, б). Процесс взаимодействия бризеров при дальнейшем увеличении скорости их движения (v(t0) ^1) также не является упругим, хотя в этих экспериментах бризеры проходят друг сквозь друга (рис. 4в). В данном случае при взаимодействии бризеров происходит излучение значительной части их энергии (рис. 4в, t > 40, 8). В первой группе экспериментов наблюдается образование сдвоенного осциллирующего возмущения с дополнительной динамикой продольно-поперечного колебания (рис. 4а). При средних скоростях движения (0,39 < |v(t0)| < 0,63) сталкивающихся бризеров наблюдаются процессы объединения и последующего разрушения системы бризерных полей. Заметим, что, как было указано во введении, аналогичные результаты описаны в работе [6] в случае пульсирующих солитонов. Однако результаты настоящей работы показывают, что в отличие от случая пульсонов, разрушающихся как в свободном состоянии [1; 2; 19], так и при взаимодействии [6; 20], бризерные решения вида (9) являются более устойчивыми. Заметим также, что неупругие взаимодействия (рис. 4) бризерных решений вида (9) в рамках УСГ можно объяснить, в частности, тем, что они получены в работе [14] методом усреднения лагранжиана и являются приближенными решениями. Тем не менее описанные процессы нуждаются в качественном анализе. Результаты экспериментов по взаимодействию однотипных (^right(t0) = Vlejt(t0)) бризеров 0(3) НСМ, так называемых возмущенных (ш = 0) решений, как и в одномерном случае [7] сводятся к их слиянию в единое осциллирующее возмущение при всех задаваемых скоростях движения v(t0) взаимодействующих бризеров (рис. 5). Интересные результаты получены при взаимодействии бризеров 0(3) НСМ, отличающиеся направлением вращения (±ш) вектора Л3-поля S в пространстве блоховской сферы S2(рис. 6). Как показано на рисунке 6а, при малых скоростях движения взаимодействующих бризеров (|v(t0) < 0,41|) имеют место процессы их столкновения и взаимного отражения. В этом случае в резонансной зоне проекции изотопических спинов S(s1,s2,s3) взаимодействующих бризеров на комплексную плоскость S^ (рис. 3в) не коллинеарны и вращаются в противоположных направлениях: S^ot(t^) [8]. В работе [8] при исследовании столкновения топологических решений было показано, что в этом случае происходит столкновение и отражение солитонов. Но при 0,41 < |v(to)| ^ 1 наблюдается однотипное нарушение симметричной эволюции системы, где в каждой серии экспериментов происходит разрушение бризерного солитона с отрицательным значением —ш (рис. 6б и 6в). При больших значениях v(t0) ^ 1 (рис. 6в) после взаимодействия наблюдается скачкообразное увеличение скорости движения взаимно-отраженных осциллирующих решений — бризера с положительным значением +ш и пульсирующего сгустка энергии, образовавшегося после разрушения бри-зера с отрицательным значением —ш. Выявленные свойства также нуждаются в строгом теоретическом анализе. В последней серии экспериментов по взаимодействию разнотипных бризеров — 0(3) НСМ (y(t0+ т)) и УСГ (^(t) = 0) наблюдается процесс объединения бризер-ных солитонов (рис. 7). Но в данном случае, в отличие от экспериментов, описанных на рисунках 4 и 5, в резонансной зоне изоспиновая структура бризерного поля УСГ приобретает дополнительную вращательную динамику. Таким образом, происходит так называемое «поглощение» бризера УСГ возмущенным бризером 0(3) НСМ, после которого наблюдается периодическое излучение лишней энергии объединенного бризера в виде линейных радиально-симметричных волн. Заключение В рамках (2 + 1)-мерной анизотропной 0(3) НСМ проведено численное моделирование процессов лобового столкновения локализованных осциллирующих (бризерных) решений вида (9). Численные эксперименты проводились при разных скоростях движения взаимодействующих бризеров и значений частоты вращения (ш = 0) вектора изотопического спина S(s1,s2,s3) в пространстве блоховской сферы S2. Для численных моделей использованы бризерные решения вида (11) и (12), полученные асимптотическими методами в работе [14]. Разработан программный модуль, позволяющий провести комплексный анализ эволюции взаимодействующих решений 0(3) НСМ теории поля с учетом ее групповых особенностей в двумерном псевдоевклидовом пространстве. Проведен анализ изоспиновой динамики, плотности (DH) и интеграла энергии (Еп) системы взаимодействующих бризеров. Целью настоящей работы было определение структурной устойчивости бризерных решений вида (9), найденных асимптотическими методами в работе [14], при их взаимодействии. Модели взаимодействующих бризеров в фазовом пространстве (2 + 1)-мерной 0(3) НСМ, полученные в настоящей работе, показывают их устойчивость при определенных значениях параметров скорости движения v(t) и частоты вращения вектора Л3-поля ш. При этом бризерные решения 0(3) НСМ, обладающие ненулевым значением ш = 0, являются более устойчивыми при взаимодействии относительно аналогичных решений УСГ (ш = 0). Результаты настоящей работы показывают также эффективность метода построения солитонных решений УСГ, предложенного в работе [21], где на основе пробного решения (9) усреднением плотности лагранжиана УСГ (8) были получены соответствующие интегральные уравнения. В работе [14] были найдены точные решения данных уравнений, на основе которых были определены выражения для фазовых параметров пробного решения вида (9). Таким образом, полученные в работе [14] и в настоящей работе результаты показывают возможность применения вышеописанного метода, апробированного в рамках УСГ и 0(3) НСМ, также для построения других видов солитонных решений.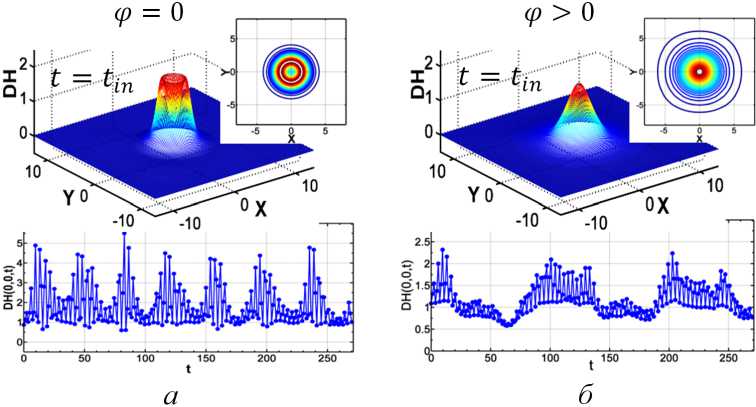
Список литературы Численное моделирование взаимодействия бризерных решений (2 + 1)-мерной 𝑂(3) нелинейной сигма-модели
- Боголюбский, И. Л. Динамика сферически-симметричных пульсонов большой амплитуды / И. Л. Боголюбский, В. Г. Маханьков // Письма в ЖЭТФ. - 1977. - Т. 25, вып. 2. - C. 120-123.
- Боголюбский, И. Л. О времени жизни пульсирующих солитонов в некоторых классических моделях / И. Л. Боголюбский, В. Г. Маханьков // Письма в ЖЭТФ. - 1976. - Т. 24, вып. 1. - C. 15-18.
- Бутрим, В. И. Особенности релаксации магнонов в легкоплоскостном антиферромагнетике в рамках сигма-модели / В. И. Бутрим, Б. А. Иванов // Физика низких температур. - 2012. - Т. 38, № 12. - C. 1410-1421. - DOI: 10.1063/1.4771980
- Киселев, В. В. Нелинейная динамика бризеров в спиральных структурах магнетиков / В. В. Киселев, А. А. Расковалов // ЖЭТФ. - 2016. - Т. 149, вып. 6. - C. 1260-1269. - DOI: 10.4213/tmf8315
- Логинов, А. Ю. Связанные фермионные состояния в поле солитона нелинейной 𝑂(3) модели / А. Ю. Логинов // Письма в ЖЭТФ. - 2014. - Т. 100, вып. 5. - C. 385-389. - DOI: 10.1134/S0021364014170093
- Маханьков, В. Г. Солитоны и численный эксперимент / В. Г. Маханьков // ФЭЧАЯ. - 1983. - Т. 14, № 1. - C. 123-180.
- Муминов, Х. Х. Взаимодействие динамических и топологических солитонов в 1𝐷 нелинейной сигма-модели / Х. Х. Муминов, Ф. Ш. Шокиров // Доклады АН РТ. - 2016. - Т. 59, № 3-4. - C. 120-126.
- Муминов, Х. Х. Изоспиновая динамика топологических вихрей / Х. Х. Муминов, Ф. Ш. Шокиров // Доклады АН РТ. - 2016. - Т. 59, № 7-8. - C. 320-326.
- Муминов, Х. Х. Математическое моделирование нелинейных динамических систем квантовой теории поля / Х. Х. Муминов, Ф. Ш. Шокиров. - Новосибирск: Изд-во СО РАН, 2017. - 375 c.
- Муминов, Х. Х. Многомерные динамические топологические солитоны в нелинейной анизотропной сигма-модели / Х. Х. Муминов // Доклады АН РТ. - 2002. - Т. 45, № 10. - C. 28-36. -
- DOI: 10.1134/S0021364014170093
- Рысаева, Л. Х. Вероятность нарушения РТ-симметрии при столкновении бризеров со случайными фазами в модели плоского РТ-симметричного каплера / Л. Х. Рысаева, С. В. Сучков, С. В. Дмитриев // Письма в ЖЭТФ. - 2014. - Т. 99, вып. 10. - C. 664-668. -
- DOI: 10.7868/S0370274X1410004X
- Самарский, А. А. Математическое моделирование: Идеи. Методы. Примеры / А. А. Самарский, А. П. Михайлов. - М.: Физматлит, 2001. - 320 c.
- Федоров, Э. Г. Взаимодействие электромагнитных бризеров в массиве углеродных нанотрубок / Э. Г. Федоров, А. В. Пак, М. Б. Белоненко // Физика твердого тела. - 2014. - Т. 56, вып. 10. - C. 2044-2049.
- Шокиров, Ф. Ш. Математическое моделирование бризеров двумерной 𝑂(3) нелинейной сигма-модели / Ф. Ш. Шокиров // Математическое моделирование и численные методы. - 2016. - № 4 (12). - C. 3-16. -
- DOI: 10.18698/2309-3684-2016-4-316


