Численное моделирование взаимодействия газовзвеси с ударной волной континуальными математическими моделями с идеальной и диссипативными несущими средами

Моделирование гидродинамических процессов в связи с нелинейностью систем уравнений связано с применением различных численных алгоритмов [1]–[28]. В статье [3] представлена конечно-разностная модель газовой динамики применительно к задачам физики атмосферы. В работе [5] исследована возможность применения математической модели исследования и прогнозирования погоды для изучения характеристик пограничного слоя атмосферы и его изменений над крупным промышленным городом в условиях зимнего антициклона. Получено, что математическая модель относительно хорошо описывает наблюдаемую структуру пограничного слоя. В публикации [6] проводится анализ результатов в области численного моделирования тепломассообмена в различных объектах атомной энергетики. В исследовании [7] на основе конечно-разностного решения уравнений Навье—Стокса разработан комплекс программ моделирования гидродинамического воздействия водных потоков на берегозащитные сооружения и прибрежные конструкции. В статье [8] проводится верификация турбулентной модели для различных струйных течений, проведены численные исследования осесимметричных струй для различных температур и скоростей течения.

Одним из развивающихся разделов современной механики жидкости и газа является динамика неоднородных сред. В монографии [9] представлены теоретические основы механики многофазных сред, описаны различные методики моделирования течений неоднородных сред, в том числе многофазных сред (смесей), компоненты которых имеют различное агрегатное состояние. В монографии [10] разработаны одномерные модели динамики газовзвесей, взвешенных в газе твердых частиц или жидких капель, с невязкой несущей средой. В монографии [11] представлены одномерные и плоские стационарные и нестационарные математические модели запыленных сред. В работе [12] разработана математическая модель и ее компьютерная реализация, позволявшая исследовать акустические процессы в неоднородных средах. Модель описывает процессы тепломассообмена для капли жидкости, покрытой эластичной оболочкой, в центре которой находится парогазовый пузырь. Система уравнений волновых процессов включала в себя уравнения теплопроводности и конвективной диффузии, а также граничные условия, описывающие межфазный тепло- и массоперенос между парогазовой смесью, жидкой фазой, вязкоупругой оболочкой и жидкостью–носителем. В публикации [13] рассмотрена задача моделирования сейсмического поля в неоднородной слоистой среде с включениями, построены алгоритмы моделирования сейсмических процессов в неоднородных средах с учетом влияния электромагнитного поля. В публикации [14] с использованием трехмерной нелинейной математической модели изучаются динамические процессы в однородной среде с примесью, изучены особенности трансформации примеси в море, вызванные действием переменного ветра и атмосферного давления при наличии морских течений. В исследовании [15] представлена математическая модель и численный алгоритм, а также программное средство для проведения вычислительных экспериментов, разработанные на основе методов гидродинамики для моделирования процессов многокомпонентной фильтрации. В исследовании [16] описан метод Годунова, предназначенный для расчетов течений смеси на криволинейных сетках, проведен анализ уравнений математической модели, показана их гиперболичность. В публикации [17] исследованы задачи взаимодействия ударной волны с ограниченным слоем газовзвеси. Для расчетов используется гибридный метод крупных частиц второго порядка аппроксимации по пространству и времени. Исследованы зависимости ослабления ударной волны слоем газовзвеси. Изучены ударно-волновые структуры в двумерных областях и влияние на них релаксационных процессов. Без применения полного гидродинамического подхода, используя уравнения акустики в исследовании [18] численно моделировалось конденсация атмосферного аэрозоля, рассмотрены различные механизмы конденсации капель аэрозоля. В работе [19] численно моделировалось нестационарное течение газа с дисперсными включениями в гиперзвуковой ударной трубе с момента начала движения возмущения до момента формирования стационарного течения. Для газа численно решалась полная гидродинамическая система уравнений, в двухмерном осесимметричном приближении, с учетом сжимаемости газа, но без учета вязкости газа. Динамика частиц описывалась с учетом полей скорости газа с помощью обыкновенных дифференциальных уравнений учи- тывающих газодинамические силы несущей среды, приложенные к частицам. Влияние частиц на течение несущей среды не учитывались, что является корректным для описания динамики дисперсной среды лишь при малых объемных содержания дисперсной компоненты [9]. В работе [20] моделировалось взаимодействие ударной волны с объемом газокапельной взвеси. Получена математическая модель двухкомпонентной сжимаемой среды. В публикации [21] разработана модель течения для численного моделирования многофазных течений с фазовыми переходами. Модель представляет собой многокомпонентную систему уравнений невязкой среды. В статье [22] численно моделировалась динамика процесса детонации, инициируемой ударным схлопыванием заполненной газом эллипсоидальной полости, заложенной во взрывчатом веществе с конденсированной фазой. Математическая модель описывала динамику многокомпонентной смеси, для численного решения уравнений математической модели использовалась конечно-разностная схема Годунова. В публикации [23] получена двухмерная численная модель детонации в неоднородной среде, основанная на методе Эйлера—Лагранжа и учитывающая дробление капель. Модель учитывала межфазный обмен массой, импульсом и межфазный теплообмен. Было обнаружено существенное влияние межфазного взаимодействия на интенсивность процесса детонации.

Из анализа публикаций в отечественных и зарубежных периодических изданиях следует, что при разработке математических моделей динамики неоднородных сред основной задачей является описание эффектов взаимодействия компонент смеси. В различных исследованиях взаимодействие компонент в движущихся смесях сопровождается не только механическими, но и термодинамическими или даже химическими процессами. При этом во многих исследованиях для упрощения математических моделей пренебрегают геометрией или же полным описанием гидродинамических свойств течений. Таким образом, дальнейшее развитие математического моделирования гидродинамики неоднородных сред может состоять как в наиболее полном описании гидродинамики процесса, так и в более подробном описании разнородных эффектов межкомпонентного взаимодействия в движущихся смесях.

Для моделирования динамики неоднородных сред в литературе существует несколько подходов [9] . В равновесном подходе динамики неоднородных сред за счет введения коэффициентов, дающих поправки на неоднородность, динамика смеси описывается как динамика однородной жидкости или газа. Диффузионный подход предполагает, что уравнения сохранения массы описывают непрерывность плотности отдельно каждой компоненты, а уравнения сохранения импульса и энергии интегрируются для всей смеси. Также существует континуальный подход, в котором для каждой компоненты смеси решается полная гидродинамическая система уравнений, включающая в себя уравнения непрерывности плотности, массы и энергии с учетом взаимодействия компонент смеси в процессе движения.

При движении газодисперсной среды (газовзвеси) движение дисперсной компоненты формируется под действием движения несущей среды. Но при этом на несущую среду оказывает воздействие дисперсная компонента смеси. Таким образом при близких массовых долях компонент смеси возможны взаимообратные эффекты, выявить которые можно лишь при моделировании процесса математическими моделями, учитывающими взаимодействие компонент. В данной работе проводится сопоставление математических моделей динамики неоднородных сред, реализующих континуальный подход динамики многофазных сред (газовзвесей). Актуальность данного исследования заключается в том, что динамические процессы в газовзвесях возникают в различных областях техники, в частно- сти ударно-волновые процессы встречаются в технологиях экранирования промышленных взрывов аэрозольными завесами, в различных агрегатах аэрокосмической техники. Интерес к развитию математических моделей динамики газовзвесей вызван необходимостью моделирования такого рода процессов в различных аппаратах и промышленных технологиях. Новизна исследования заключается в том, что сопоставляются расчеты ударно-волнового взаимодействия однородного газа с газовзвесью, полученные различными математическими моделями динамики газовзвесей. В работе исследованы течения газовзвесей при таких объемных содержаниях дисперсной фазы, когда невозможно пренебречь взаимообратными эффектами динамики неоднородной среды, как это делается в работе [19]. В данной работе для моделирования ударно-волновой динамики газовзвесей применяется модель, в которой помимо теплообмена и обмена импульсом между компонентами смеси, а также учета сжимаемости и теплопроводности несущей среды [10], учитывается вязкость газовой фазы смеси. В рамках континуального подхода моделирования динамики газовзвесей определяется влияние свойств (сжимаемость, теплопроводность, вязкость) математической модели динамики несущей среды на результаты расчетов. Сопоставление расчетов континуальных моделей несущие среды, которые отличаются между собой различными газодинамическими описаниями несущих сред, позволит определить то как параметры несущей среды влияют на межкомпонентное взаимодействие при моделировании ударно-волновых процессов в аэрозольных средах. Целью исследования является сопоставление результатов расчетов, полученных континуальными моделями с различным описанием несущей среды. Моделировались такие режимы течений газодисперсных сред, в которых возможно определить различия результатов расчетов межкомпонентного взаимодействия, полученных математическими моделями с разными описаниями динамики газовой компоненты. Задачи исследования заключаются в проведении ряда численных экспериментов для математических моделей с различными свойствами несущей среды. В рамках одного программного комплекса с помощью изменения решаемых уравнений рассматривались математические модели динамики газовзвесей с вязкой теплопроводной, невязкой теплопроводной и идеальной несущими средами. Для полученных расчетов ударно-волновой динамики газовзвесей проводится анализ влияния параметров модели.

Статья имеет следующую структуру. В разделе 1 представлены уравнения математических моделей динамики газовзвесей с идеальной и невязкой теплопроводной несущими средами, что соответствует методике моделирования описанной в монографии [10] , а также вязкой теплопроводной несущей средой. Далее в разделе 1 описан численный алгоритм решения уравнений математических моделей. Раздел 2 посвящен программной реализации численного алгоритма решения системы уравнений динамики газовзвеси. В разделе 3 приведены результаты численных экспериментов, проведенных с помощью программного комплекса, описанного в разделе 2 для реализации основной идеи работы — сопоставления различных математических моделей течений газовзвеси. Также в разделе 3 анализируются результаты моделирования динамики дисперсной компоненты и межкомпонентного взаимодействия в ударной волне при различных методиках моделирования движения несущей среды газовзвеси. В заключении приводится краткая сводка результатов, полученных в работе, и указаны направления дальнейших исследований.

1. Математическая модель

Для описания динамики дисперсных включений, распределенных дискретно, вводится понятие «средней плотности» — произведения постоянной величины «физической плотности» дисперсной фазы на объемное содержание, которое является функцией временной и пространственных переменных, что позволяет моделировать динамику совокупности частиц как однородную среду. В представленной модели смесь состоит из двух континуумов [9] — газовой и дисперсной фазы:

⁹P + ⁹ (pu) + ^{9 (}pv) = 0 \partialt \partialx \partialy

^ЭР 1 , ^{9 (}P i u i ) , ⁹⁽P i v i ) = 0

\partialt \partialx \partialy .

Уравнение (1) описывает непрерывность плотности сжимаемого газа, уравнение (2) описывает непрерывность «средней плотности» дисперсной фазы, также описываемой как сжимаемая среда [10, 11] . При моделировании ударно-волновых процессов в газе [1, 2] и газодисперсных средах [10, 11] существенным является свойство сжимаемости.

^{9 ( pU )} + I*-(pU 2 + p - T xx ) + ⁹-(puv - T xy ) = - F x + a^p, \partialt \partialx                                                                         \partialy                                                                                              \partialx

9(pv)   9 ,            *9.2         .           9p

— + 9X ^{( p}uv + p - ^T xy ^{) +} 9y ^{( pv} + p - ^T yy ) = - F y + ^a9y,

^9(pU) + ⁹ (pu ² + p) + It (puv) = - F x + a^p,                 (5)

\partialt \partialx                                                  \partialy                                                                       \partialx

^{9 ( pv ) +} It ⁽puv ⁺ p ^{) +} It (pv ^{2 +} p) = ^- F y ⁺ “?                ⁽⁶⁾

\partialt \partialx                                                   \partialy                                                                                    \partialy

Уравнения (3) и (4) в совокупности составляют систему уравнений Навье—Стокса, описывающую сохранение пространственных составляющих импульса вязкого газа, уравнения (5) и (6) составляют систему уравнений Эйлера, описывающую сохранение импульса невязкого газа. Отличие от классических уравнений гидродинамики заключается в наличии правых частей уравнений, отвечающих за обмен импульсом с дисперсной компонентой.

9(p1u1)    9      2     99p

-^t- + 9x(piUi) + 9y(piUiVi) = Fx - a9x,

9(p1v1)    9              9      2

-"эТ" + 9X(piuivi) + 9y (piv1) = Fy - а9У

Уравнения (7) и (8) описывают сохранение пространственных составляющих импульса дисперсной фазы и не зависят от вязких свойств несущей среды напрямую, а лишь опосредовано, так как в этих уравнениях присутствуют слагаемые, отвечающие за обмен импульсом между компонентами смеси.

\partiale \partialt

+ It ([e + P - T xx] u - T xy v + X^9T ) +   ([e + p - T yy ]v - T xy u + X^T ) =

\partialx                                                                                                        \partialx \partialy                                                                                                        \partialy

= —6^aXNu 1 ⁽T ^{- T} 1 ^{) / ( d ) 2 -} | F x ^{|( u -} u i ) ^{- | F} y ^{|( v -} v l )) ^{+ a}

9(pu)

^{9 (}pv) \

⁺ 9y J’

"нт +   ([e + p]u + A——) + я-([e + p]v + ^   ) = -6aANui(T - Ti)/(d)2—

\partialt \partialx                                                     \partialx \partialy                                                     \partialy

-|Fx|(u - ui) -|Fy|(v - »)) + <  ;+ ^

Se + SX:[' + p]u) + !ъ :'' + p]v) = -|Fx|(u - “1)-

\partialt \partialx                                                  \partialy

-|Fy|(v - vi)) + -

\partialx \partialy

Уравнения (9) – (11) описывают сохранение энергии вязкой теплопроводной, невязкой теплопроводной и идеальной несущих сред соответственно. В уравнениях учитывается обмен импульсом и теплообмен газа с дисперсной компонентой, в случае идеальной среды в уравнении учитывается только обмен импульсом.

+ £(e i u i ) + £(e i v i ) = Nu i ^(T - T i ),                (12)

at ox         Oy              (d) ²

Te T ⁺ °- (e i u i ) ⁺ °" (e i v i ) = ⁰

\partialt \partialx                                      \partialy

Уравнения (12) и (13) описывают сохранение энергии для вязкой теплопроводной и невязкой теплопроводных сред (12) и для идеальной среды (13) . В уравнениях применятся следующие обозначения: \rho — плотность (для несущей среды плотность газа, а для дисперсной компоненты «средняя плотность») компонент, u i , v i — составляющие векторов скорости, компонент смеси — V i , e i и T i — энергия и температура компонент смеси, p — давление газа. Индекс «1» относится к физическим величинам дисперсной компоненты смеси, переменные без индекса описывают изменение физических параметров несущей среды. Здесь \lambda, \mu, \gamma — коэффициенты теплопроводности, вязкости и постоянная адиабаты для несущей газообразной среды, I = RT i /(^ - 1) — внутренняя энергия несущей среды ( R — газовая постоянная) [2] , \tau _xx , \tau _xy , \tau _yy — составляющие тензора вязких напряжений несущей сред (14) :

p = (7 - 1)(e - p(U 2 + v 2 )/2), e = p(I + (u ² + v 2 )/2), e i = ap_MC pi ,

( du 2 A           O du 2 A           /Ou Ov A         ,

^T“ = ^p (,²dx ^- 3 Dp ^T *y = ^p 7oy ^- 3 Dp ^T xy = ^FU ⁺ ox?      ⁽¹⁴⁾

partialu partialv = ^(dx ⁺ dy) ^.

Используются обозначения: alpha — объемное содержание дисперсной фазы, C _p 1 , rho 10 — удельная теплоемкость и физическая плотность вещества твердых частиц, d — диаметр частиц, предполагается, что все частицы имеют сферическую форму. Компоненты силы межфазного взаимодействия F _x (15) и F y (16) определяются следующим образом [9] – [11] :

F x

3dCd i PV(u - u i ) 2 + (v - v i ) 2 (u - u i ) ,

F ^y = ^dCd i P^(u - u i ) 2 + (v - v i ) 2 (v - v i ) ’                    (16)

Обмен импульсом компонент смеси определяется коэффициентом сопротивления C d1 . Теплообмен и обмен импульсом состаляющих газовзвеси определяются [10] относительным числом Маха M 1 , относительным числом Рейнольдса Re 1 , относительным числом Нуссельта Nu 1 и числом Прандтля Pr 1 , выражения для определения коэффициентов взаимодействия компонент смеси имеют следующий вид (17) :

24       4              .                 . - 0.427

C di = ^C d1 Ф^(M 1 ⁾Ф⁽a^), C di = r— + R_e 0.5 ^{+ 0} - ^{4 , ф ( м}^ = ^{1 +} exp( — m1). ₆₃ ),

Ф(а) = (1 - a) ^-2 ' ⁵ , Re i = dp \ V - V i | /^, M i = | V - V i | ,

Pr i = C pi ^(A) ^-1 , Nu i2 = 2exp( - M i ) + 0/459Re 0- ⁵⁵ Pr 0' ³³ .

Для векторов скорости компонент смеси используется обозначение V = [u, v], V i = [u i ,v i ]. Система уравнений (1) , (2) , (5) – (8) , (11) , (13) описывает динамику газовзвеси с идеальной (невязкой и нетеплопроводной несущей средой) с учетом обмена импульсом между несущей средой и дисперсной компонентой. Уравнения (1) , (2) , (5) – (8) , (10) , (12) соответствуют математической модели динамики газовзвеси с несущей средой (невязким теплопроводным газом), разработанной в монографии [10] . Система уравнений (1) – (4) , (7) – (9) , (12) описывает движение газовзвеси с сжимаемой, теплопроводной и вязкой несущей средой. Система уравнений дополнялась соответствующими граничными условиями. На границах расчетной области задавались однородные граничные условия Дирихле для составляющих скорости несущей и дисперсной фазы при моделировании динамики вязкой среды и однородные граничные условия Неймана при моделировании динамики невязкой среды, для остальных функций в обоих случаях задавались однородные граничные условия Неймана [1, 2] . Для интегрирования систем уравнений применялся явным конечно-разностный метод Мак—Кормака [2] . Рассмотрим численный алгоритм на примере скалярного нелинейного дифферениального уравнения в частных производных (18) от функции f , где a(f), b(f), c(f ) — нелинейные функции:

f + Ml + М =(/).8

\partialt \partialx \partialy

Для нелинейного уравнения (18) численное решение явным конечно-разностным методом Мак—Кормака на n-ом временном слое записывается следующим образом [2] (19) :

f *     fn-i    At , n-i     n-i\    At/ ,n-i    , n-ix дn fjk = fjk - ax (aj+ik- ajk )- Ay (bjk+i- bjk ) +Atcjk , fjk = 0.5(fj*k + fjnk) - 0-5AV(a*k - a*-ik) - 0-57\7(b*k - b*k-i) + 0-5Atc*k.

Ax            Ay

Здесь At, Ax, Ay — шаги по переменной времени и пространственным направлениям.

С целью подавления численных осцилляций использовалась схема нелинейной коррекции сеточной функции (20) [3, 4] . Пусть Z _j ⁿ _,k — произвольная независимая функция на n–ом временном слое в узле j, k . Тогда алгоритм коррекции имел бы следующий вид:

Znk = Znk + «(bZj+i/2,k - bZj-i/2,k), где Zjn,kast — скорректированная функция. Данный алгоритм выполняется в случае, когда (JZn-i/2 k6Z'n+i/2 k) < 0 или (dZn+i/2 k^Zjn+3/2 k) < 0. Здесь используются обозначения 2022, т. 11, № 4 73

,7/п —7" _7" П7п — 7"   _ 7п Л7п — 7"   _ уп           ™

°Zj-1/2,k = Zj Zj-1,k ,°Zj+1/2,k = Zj+1,k Zj,k,°Zj+3/2,k = Zj+2,k   Zj+1k, где K ко эффициент коррекции. Величина шага по времени при реализации численного алгоритма выбирается исходя из условия Куранта—Фридрихса—Леви [2].

• 2.    Компьютерная реализация

Программный комплекс, с помощью которого проводились вычислительные эксперименты в данной работе, реализует математическую модель, составленную из уравнений (1) – (4) , (7) – (9) , (12) , описывающую динамику газовзвеси с вязкой, сжимаемой, теплопроводной несущей средой. Изменения в структуре численно интегрируемых уравнений позволяет проводить расчеты как для математической модели динамики газовзвеси с невязкой теплопроводной несущей средой, описанной в монографии [10] , так и для математической модели, в которой отсутствует вязкость и теплопроводность несущей среды.

В вычислительной гидродинамике компьютерная реализация конечно-разностной модели течения жидкости или газа состоит из следующих частей: определение геометрических параметров физической области течения, формирование конечно-разностного разбиения области моделирования, задание граничных условий и непосредственно самого процесса численного интегрирования системы аэро-гидродинамических уравнений. В данной работе компьютерная программа написана на языке программирования Fortran. Программный код, составляющий компьютерную модель, представляет собой набор последовательно реализуемых компонент. Алгоритм программной реализации численной модели динамики га-зовзвеси имеет следующую последовательность:

• 1)    задаются физические параметры газа и твердых частиц;

• 2)    из файлов считываются начальные значения функций, геометрия области и характеристики ее сеточного разбиения;

• 3)    строится сеточное разбиение области течения смеси;

• 4)    определяется значение величин межфазного обмена импульсом и межфазного теплообмена;

• 5)    реализуется конечно-разностное решение уравнений динамики смеси;

• 6)    проводится нелинейная коррекция сеточных функций.

• 7)    значения искомых функций в узлах сетки на каждом временном слое выводятся в файл.

• 3.    Вычислительные эксперименты

  В работе исследовалось распространение прямого скачка давления из однородного газа в газовзвесь, моделировалось течение происходящее в ударной трубе [1, 10] . С учетом наличия поверхности раздела сред «неоднородная среда — однородная среда», наиболее адекватно такой процесс может быть описан только в рамках континуального подхода динамики неоднородных сред [10, 11] . Ударная труба представляет собой канал, разделенный мембраной, часть канала заполнена газом с меньшим давлением — камера низкого давления, часть канала заполнена газом имеющим большее давление — камера высокого давления. В отличии от классических работ по ударным трубам предполагалось, что в камере низкого давления расположена газовзвесь — взвесь твердых частиц. Начальный разрыв давления задавался через температуру газа T = T 20 = 2 • T 10 ,x <  L/2, таким образом давление в камере высокого давления ударной трубы вдвое превосходит давление газа в камере низкого давления Р 20 = 2 • p io = 196 кПа. Длина канала L=2 м, ширина канала h=0.1 м. Несущая среда описывалась как воздух. Физическая плотность материала дисперсной компоненты и теплоемкость материала дисперсной компоненты составляла \rho 10 =2700 кг/м ³ , p1 =903 Дж/кг \cdot К, дисперсность частиц — d =2 мкм.

Вычисление значений параметров неоднородной среды на каждом последующем временном слое осуществляется последовательным применением шагов 4)–6). Программный комплекс состоит из нескольких компонент: подпрограмма задания граничных условий, подпрограмма формирования конечно-разностного разбиения физической области, подпрограмма расчета взаимодействия компонент смеси, основная численного решения уравнений динамики газовзвеси.

На рис. 1 изображена структура программы моделирования динамики аэрозолей. Расчеты течения газовзвеси формируются программой численного решения уравнений динамики неоднородной среды, для функционирования основной программы необходимы подпрограммы: подпрограмма формирования сеточного разбиения физической области, подпрограмма задания граничных условий системы уравнений математической модели, подпрограмма межкомпонентного взаимодействия, описывающая обмен импульсом и теплообмен компонент смеси. Для работы объектного модуля необходима информация о физических параметрах моделируемой смеси и геометрических параметрах физической области и количестве узлов конечно-разностного разбиения области. Начальные параметры содержат-

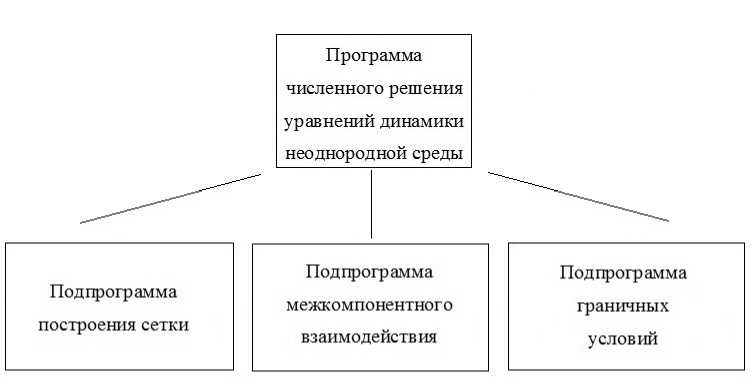
Рис. 1. Структура программного комплекса моделирования динамики двухфазной смеси ся в двух файлах: файл с данными о физических свойствах движущихся сред и файл с данными области течения и параметрами ее конечно-разностного разбиения. Вызов подпрограммы построения сетки осуществляется перед циклом численного решения системы уравнений в основной программе, построения конечно-разностного решения явного метода Мак—Кормака. Вызов подпрограммы граничных условий осуществляется на каждом временном слое в основной программе. В основной программе реализуются метод конечноразностного решения и схема нелинейной коррекции сеточных функций, необходимая для преодоления численных осцилляций и применяемая после получения численных решений на каждом временном слое. После вычисления функций динамики компонент смеси рассчитываются величины межкомпонентного взаимодействия. Вычисленные на предыдущем временном слое значения межкомпонентного обмена импульсом и теплообмена применяются при определений значений искомых функций на следующем временном слое. Функции динамики компонент смеси в программе задаются двухмерными динамическими массивами двойной точности (double precision). Файл с начальными значениями параметров неоднородной среды считывается в основной программе. При написании алгоритма численного решения для математических операций применялись встроенные функции языка Fortran. При помощи оператора COMMON осуществляется связь переменных и массивов, которые используются одновременно и в основной программе расчета динамики газовзвеси, а также во вспомогательных подпрограммах. В основной программе на каждом временном слое с помощью оператора CALL производится вызов вспомогательных подпрограмм. Таким образом, структура кода программы, численного решения уравнений континуальной математической модели динамики неоднородной среды, отличается от кода программы моделирования динамики однородной среды наличием дополнительной подпрограммы расчета взаимодействия компонент смеси.

Программный комплекс, примененный в данной работе, разработан на основе континуального подхода [9] методики моделирования динамики дисперсных сред в сжимаемой газовой среде [10] в процессе работы над диссертацией [24]. Программный комплекс моделирования динамики газовзвеси с учетом взаимодействия компонент смеси был развитием уже существовавшего программного комплекса численного моделирования динамики одиночной частицы в сжимаемом газе [4]. Развитие программного комплекса заключалось в добавлении расчета полной гидродинамической системы уравнений движения для дисперсной компоненты и в учете взаимообратного (воздействующего на каждую компоненту смеси) межкомпонентного взаимодействия. В работе [25] проводится сопоставление физического эксперимента по ударно-волновому течению газовзвеси с численными расчетами, полученными вышеописанным программным комплексом.

Рассмотрим результаты применения конечно-разностного метода (15) при интегрировании системы уравнений (1) – (13) программным комплексом, описанным в разделе 2.

• а)    невязкая среда                            б) вязкая среда

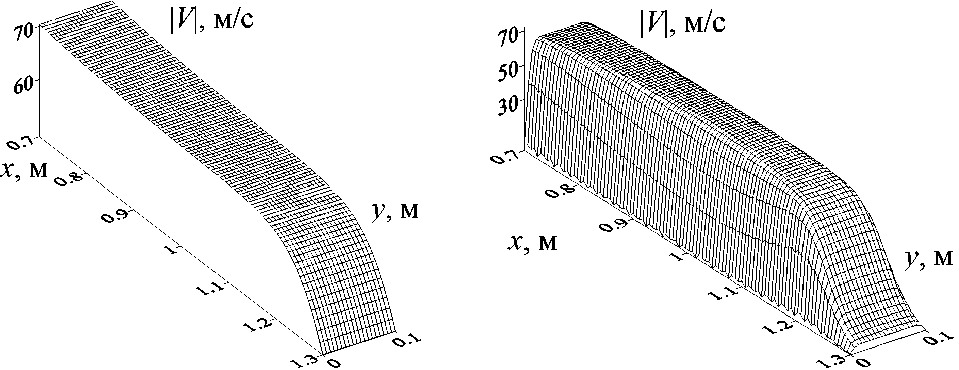
Рис. 2. Двухмерное распределение модуля скорости газа, при распространении ударной волны

На рис. 2 изображено распределение модуля скорости газа V = Vu2 + v2 при моделировании движения ударной волны в канале с однородными граничными условиями Неймана для невязкой среды (рис. 2а) и с однородными граничными условиями Дирихле (рис. 2б) для вязкой среды. Можно наблюдать равномерное в y-направлении распределение скорости для невязкой среды, в случае движение ударной волны в канале в вязкой среде, можно наблюдать «параболический» [1, 2] профиль скорости несущей среды. При моделировании течений сплошных сред в узких каналах более предпочтительным, чем модель невязкой среды, является описание течения с учетом пристеночной вязкости в канале [1, 2].

а) Пространственное распределение

модуля скорости газа

• б)    Пространственное распределение модуля скорости дисперсной фазы

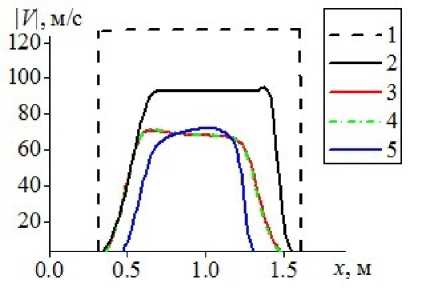
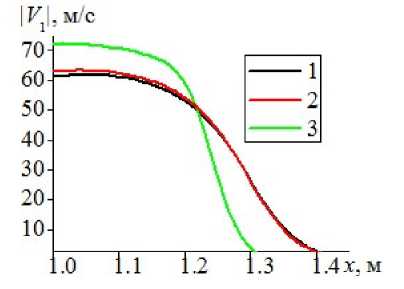
Рис. 3. Сопоставление расчетов модуля скорости спутного потока газа и модуля скорости дисперсной фазы для различных математических моделей

На рис. 3a представлены сопоставления скорости газа как при распространении ударной волны из газа в газовзвесь, так и в однородной среде, на оси симметрии канала, где достигаются наибольшие значения скоростей. Кривые 1 и 2 — соответственно аналитическое решение скорости спутного потока, полученное для идеального газа в работе [1] и численный расчет для распространения ударной волны в идеальном газе. Аналитически рассчитанное решение имеет большую интенсивности спутного потока газа. Кривые 3 и 4 — результаты расчетов динамики ударной волны из однородного газа в газовзвесь, полученные по моделям идеальной несущей среды и теплопроводной несущей среды [10] . Кривая 5 — результаты расчетов распространения ударной волны из однородного газа в газовзвесь с учетом вязкости несущей среды. Численные расчеты динамики несущей среды до взаимодействия ударной волны с газовзвесью по математическим моделям с идеальной и невязкой теплопроводной несущей средой [10] совпадают с численными расчетами спутного потока в однородном идеальном газе. Наибольшее значение скорости дисперсной компоненты при движении ударной волны по газовзвеси достигается в расчетах по математической модели с вязкой несущей средой (рис. 3, кривая 3). Скорость дисперсной компоненты при расчетах по математической модели с теплопроводной невязкой несущей средой [10] (кривая 2) немного больше, чем скорость дисперсной компоненты с идеальной несущей средой (кривая 1). Модуль скорости дисперсной компоненты при учете вязкости несущей среды имеет большее значение, при этом можно наблюдать, что непосредственно ударно-волновое возмущение по дисперсной фазе распространяется с меньшей скоростью относительно расчетов с невязкими несущими средами.

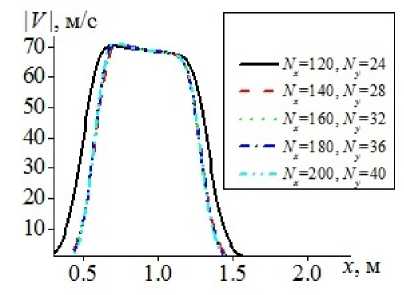
На рис. 4а представлено распределение модуля скорости газа в канале при различных сеточных разбиениях области в момент времени t=1 мс, для математической модели с несущей средой (идеальным газом). Для разбиений сетки N _x =120, N y =24 ширина области затронутой спутным потоком газа за ударной волной в камере низкого давления и спутным потоком за волной разряжения, в камере высокого давления, составляет L _w =1282 мм, для разбиений расчетной области N _x =140, N y =28, N _x =160, N y =32, N _x =180, N y =36, N _x =200,

а) идеальная несущая среда

Рис. 4. Пространственное распределение модуля скорости газа, для различных сеточных разбиений

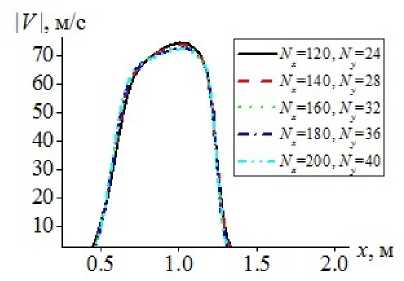
б) вязкая несущая среда

N _y =40 ширина зоны движения газа составляет соответственно L _w =1083 мм, L _w =1053 мм, L _w =1031 мм, L _w =1026 мм. Для данных сеточных разбиений скорости ударной волны составляют соответственно \theta = 521 м/c, \theta = 445 м/c, \theta = 430 м/c, \theta = 418 м/c, \theta = 416 м/c. Аналогичны результаты для математической модели с вязкой теплопроводной несущей средой в тот же момент времени изображены на рис. 4б Для разбиения расчетной области N _x =120, N _x =24 ширина области затронутой движением газа составляет L _w =892 мм для разбиений расчетной области N _x =140, N _y =28, L _w =872 мм, N _x =160, N _y =32, L _w =858 мм, N _x =180, N y =36, L _w =852 мм, N _x =200, N y =40, L _w =848 мм ширина зоны движения газа составляет соответственно L _w =1083 мм, L _w =1053 мм, L _w =1031 мм, L _w =1026 мм. Скорости движения ударных волн для указанных разбиений составляют \theta = 314 м/c, \theta = 305 м/c, \theta = 298 м/c, \theta = 294 м/c, \theta = 292 м/c. При измельчении сеточных разбиений как для невязкой, так и для вязкой несущих сред происходит равномерное уменьшение скорости ударно-волнового возмущения и области, затронутой движением газа — ударной волны в камере низкого давления и волны разряжения в камере высокого давления.

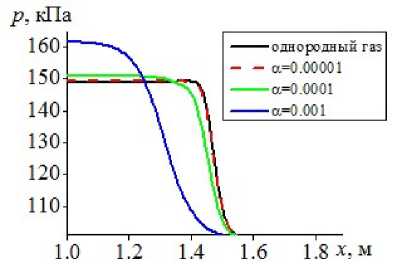
а) идеальная несущая среда

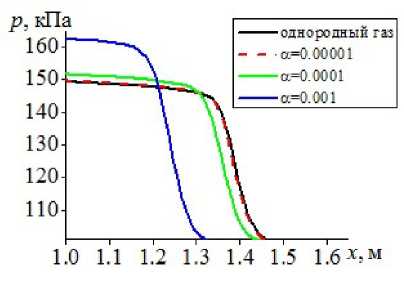
б) вязкая несущая среда

Рис. 5. Пространственное распределение давления газа для различных объемных содержаний дисперсной фазы и однородной среды

На рис. 5 представлены пространственные распределения давления в ударной волне, движущейся в однородном газе и газовзвесях с различными объемными содержаниями дисперсной фазы, для математических моделей несущей среды, описываемой как идеальный

а) однородный газ

б) газовзвесь с объемным содержанием дисперсной компоненты \alpha=0.001

Рис. 6. Пространственное распределение температуры газа при моделировании однородной и неоднородной сред, кривые: 1 — идеальная несущая среда, 2 — невязкая теплопроводная несущая среда, 3 — вязкая несущая среда газ (рис. 5а) и вязкий теплопроводный газ (рис. 5б). Для объемного содержания дисперсной фазы \alpha=0.0001 скорость ударной волны в расчетах по модели несущей среды (идеального газа) составляет 99.67% от скорости движения однородного газа, для модели динамики вязкого теплопроводного газа скорость ударной волны для того же объемного содержания дисперсной фазы составляет 94.36% от скорости движения ударной волны в однородном вязком газе. При объемном содержании дисперсной фазы \alpha=0.001 скорость ударной волны в расчетах, проведенных для несущей среды (идеального газа), составляет 86% от скорости движения однородного газа, для модели динамики вязкого теплопроводного газа скорость ударной волны составляет 69.9% от скорости движения ударной волны в однородном вязком газе.

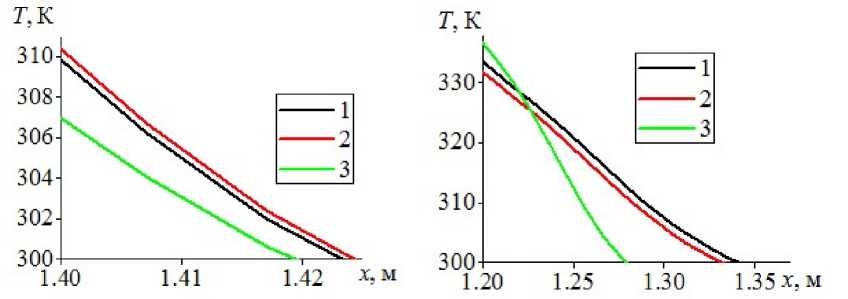
На рис. 6 изображены распределения температуры газа вдоль координаты x вблизи переднего края ударной волны в однородном газе (рис. 6а ) и в газовзвеси (рис. 6б ), полученные для различных математических моделей динамики газа. При моделировании распространения возмущения поля температуры в однородном газе скорость распространения возмущения в невязком теплопроводном и вязком теплопроводном газе составляют 99.71% и 97.62% от скорости распространения возмущения в идеальном газе. В газовзвеси с объемным содержанием дисперсной фазы \alpha=0.001 скорость движения возмущения поля температуры газовой компоненты газовзвеси в невязкой теплопроводной среде, которая рассматривается в качестве газовой фазы при составлении математических моделей в монографии [10] и в вязком теплопроводном газе составляют соответственно 97.26% и 81.33% от скорости движения возмущения температуры несущей среды рассчитанной по модели динамики идеального газа. Таким образом выявлено, что для континуального подхода моделирования, учитывающего температурную неравновесность несущей среды и дисперсной фазы, влияние, которое оказывает дисперсная компонента на распространение ударно-волнового возмущения полей давления и температуры несущей среды имеет существенные отличия при расчетах с газовой компонентой — вязкой теплопроводной средой, невязкой теплопроводной и идеальной средой.

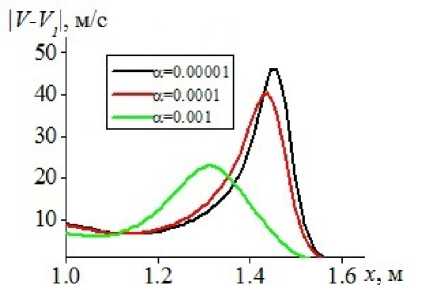
На рис. 7 представлены распределения величин модуля скоростного скольжения | V - V 1 1 = ^y (u — u i ) 2 + (v — v i ) 2 для газовзвесей с различными объемными содержаниями дис- 2022, т. 11, № 4 79

а) идеальная несущая среда

Рис. 7. Пространственное распределение модуля межфазного скоростного скольжения в газовзвесях с различным объемным содержанием дисперсной компоненты

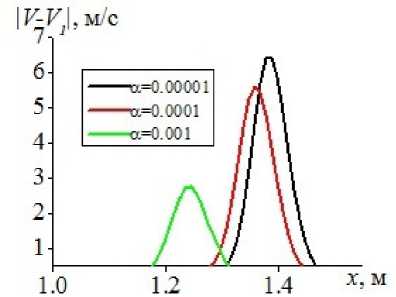
б) вязкая несущая среда

персной фазы. Величина скоростного скольжения существенно выше в модели идеального газа (рис. 7а ). Меньшая интенсивность скоростного скольжения в вязкой среде (рис. 7б ) может объясняться большим межфазным взаимодействием, в связи с чем менее существенны различия в скоростях компонент двухфазной смеси.

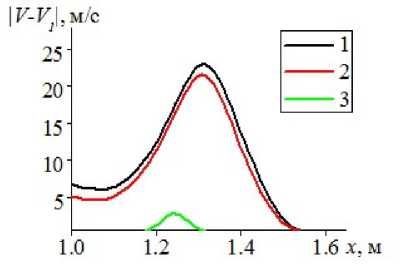
Рис. 8. Пространственное распределение модуля скоростного скольжения, кривые: 1 — идеальная несущая среда, 2 — невязкая теплопроводная несущая среда, 3 — вязкая несущая среда

Интенсивность скоростного скольжения рис. 8 при моделировании динамики несущей среды моделями идеального газа и невязкого теплопроводного газа имеет близкое значение, существенно большее, чем в вязкой среде. Данная закономерность демонстрирует, то, что при моделировании движения ударной волны по газовзвеси в канале определяющим фактором является вязкость несущей среды, а такое свойство несущей среды как теплопроводность имеет существенно меньшее значение.

На рис. 9 представлено пространственное распределение величины кинетической энергии несущей среды газовзвеси \rho V ² (рис. 9а ) и дисперсной компоненты \rho 1 V ² ₁ (рис. 9б ) при распространении ударной волны из однородного газа в газовзвесь с объемным содержанием дисперсной компоненты \alpha=0.001, для различных моделей динамики несущей среды: кривая 1 — идеальный газ, кривая 2 — невязкий теплопроводный газ, кривая 3 — вязкий теплопроводный газ. При моделировании несущей среды как невязкой теплопроводной и при моделировании несущей среды как идеальной кинетическая энергия несущей среды достигает больших максимальных значений, чем в случае учета вязкости газовой компо-

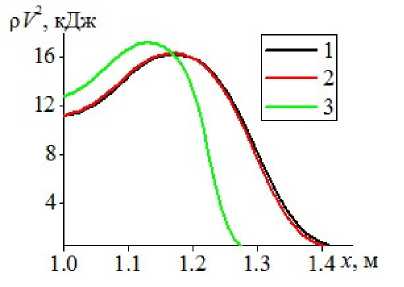
а) несущая среда

Рис. 9. Пространственное распределение кинетической энергии компонент газовзвеси

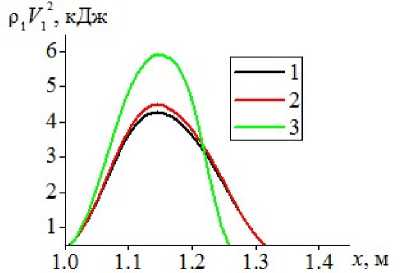
б) дисперсная компонента

ненты. При этом максимальное значение кинетической энергии дисперсной фазы в ударной волне от соответствующей величины для модели несущей среды (идеального газа) для модели вязкого газа составляет 138.76%, а для модели невязкого теплопроводного газа — 105.3 % соответственно. Столь существенное отличие в кинетической энергии дисперсной компоненты может иметь критическое значение при моделировании процессов отражения промышленных взрывов применяемых в геотехнолгиях [10] . Сопоставление численных расчетов кинетической энергии дисперсной компоненты и скоростного скольжения газовой и дисперсной фаз смеси в ударной волне демонстрирует, что в вязкой среде межфазное взаимодействие, которое является определяющим при моделировании смесей с равными массовыми долями компонент, имеет большую интенсивность, чем в невязких средах. Что является более правильным с точки зрения физики таких процессов, так как существующие в природе газы и жидкости являются вязкими, в то время как отсутствие вязкости или теплопроводности является допущением, применяемым при разработке математических моделей динамики сплошных сред.

Заключение

В работе проведено сопоставление численных расчетов распространения ударной волны из однородного газа в газовзвесь, полученных для различных математических моделей динамики несущей среды. В работе выявлено, что при моделировании динамики вязкой теплопроводной среды величины скоростного скольжения фаз смеси существенно меньше, чем аналогичные величины при описании несущей среды как идеальной. Определено, что при моделировании ударно-волновой динамики газовзвесей в каналах, влияние вязкости несущей среды наиболее существенный фактор взаимодействия газовой и дисперсной компонент смеси. При описании газовой компоненты газовзвеси как вязкой среды межфазное скоростное скольжение достигает меньших величин, чем в случае невязкой несущей среды. Также при учете вязкости несущей среды кинетическая энергия дисперсной компоненты имеет большую величину. Учет теплопроводности невязкой несущей среды также приводит к результатам расчетов с несколько меньшим скоростным скольжением фаз и большей кинетической энергией дисперсной компоненты в сравнении с результатами, полученными для несущей среды — идеального газа. Данные эффекты можно объяснить большей интенсивностью взаимодействия между компонентами смеси при учете вязких напряжений газа в ударно-волновом течении. Представленные сопоставления моделей показали, что в зависимости от выбора математической модели описания несущей среды могут наблюдаться важные (при расчете технологических процессов и агрегатов) отличия в интенсивности межкомпонентного взаимодействия и кинетической энергии дисперсной компоненты в ударно-волновом течении. Таким образом данное исследование выявило, что в континуальном подходе динамики неоднородных сред при моделировании динамики несущей среды системами уравнений Навье—Стокса и Эйлера результаты расчетов, кроме отличий в полях скоростей несущей среды, отличаются также интенсивностью взаимодействия компонент в моделируемых течениях. Выявленные закономерности, возможно использовать при разработке вычислительных моделей скоростных потоков в газовзвесях с большим объемным содержанием дисперсной фазы. Дальнейшим развитием представленной математической модели динамики газовзвесей можно предположить увеличении геометрии с плоской до трехмерной, а также учет взаимодействия между частицами дисперсной компоненты смеси.

Работа выполнена в рамках государственного задания ФИЦ КазНЦ РАН по теме «Развитие динамики многофазных сред, аэрогидроупругих систем и механики оболочек с приложениями в машиностроении и нефтедобыче» № 121021800126-4.