Численное моделирование задачи вытеснения магнитного поля при течении электропроводной жидкости в плоском МГД-канале

Развитие термоядерных реакторов, например, использование в конструкции бланкетов-размножителей, предназначенных для воспроизводства трития, порождает новые вызовы в изучении магнитогидродинамических (МГД) процессов в жидких металлах, таких как литий (Li) или его сплавы со свинцом (PbLi) [1, 2] . Существенный задел в этой области сделан в исследовании МГД-эффектов в постоянных сильных магнитных полях [3, 4] . Численное моделирование таких систем часто проводится в рамках «безындукционного МГД приближения», при котором индуцированное магнитное поле b пренебрежимо мало в сравнении с приложенным внешним B 0 . Большинство задач, связанных с моделированием МГД-эффектов в термоядерных реакторах, характеризуются значениями магнитного числа Рейнольдса Re m = U 0 L/X в диапазоне от 1.3 х 10 ⁴ до 1.7 х 10 ¹ [1, 2] (здесь U ₀ — масштаб скорости, L — линейный масштаб, λ = (σµ) ^{- 1} — коэффициент магнитной диффузии, где σ — электропроводность, µ — абсолютная магнитная проницаемость). Верхняя граница применимости «безындукционного приближения» оценивается величиной Re m ~ 0.1 [1, 2] , что позволяет использовать его для математической постановки задач [3] .

Для обеспечения надежной и безопасной эксплуатации термоядерных реакторов необходимо подвергать анализу не только установившиеся, но и переходные режимы работы. Одним из наиболее критичных переходных процессов является срыв плазмы (plasma disruption), который представляет собой быструю потерю магнитного удержания, сопровождающуюся резким падением температуры (thermal quench) и последующим стремительным затуханием тока плазмы (current quench) [5 –7] . Этот процесс, развивающийся на временном масштабе τ порядка десятков миллисекунд, порождает интенсивные импульсные электромагнитные поля. Быстрое затухание тороидального тока плазмы приводит к резкому изменению полоидальной компоненты магнитного поля, амплитуда которого может достигать значений B 0 « 1 Тл [8] .

Изменение полоидального магнитного поля приводит к возникновению вихревых токов в проводящих элементах реактора, например, в бланкетах и диверторах. Взаимодействие этих токов с основным тороидальным магнитным полем реактора вызывает появление значительных сил Лоренца. Эти силы создают импульсные механические нагрузки, которые могут привести к возникновению критических напряжений в элементах конструкции и оказать существенное влияние на гидродинамику жидкого металла. В таких режимах оценивать степень влияния индукционных эффектов стоит с помощью отношения скорости нарастания магнитного

Статья опубликована в открытом доступе по лицензии CC BY 4.0

поля y = В 0 /т к характерному значению его диффузии — А. Тогда магнитное число Рейнольдса Re m = 7/А будет достигать десятков единиц и преимущественно выражаться его импульсным воздействием. Применение численных моделей с использованием безындукционного приближения для воспроизведения процессов в таких МГД-системах становиться невозможным [9] .

В [10, 11] проведены упрощенные оценки поведения потоков проводящей жидкости в быстро меняющихся силовых полях. В работе [10] найдены аналитические одномерные решения для поля скорости и магнитной индукции в бесконечном изолированном канале при допущении, что магнитное поле бесконечно затухает. Влияние экспоненциального затухания его полоидальной компоненты за конечное время т = 60 мс на поведение потока проводящей жидкости рассмотрено в [11] с существенным упрощением в постановке гидродинамической части задачи. В [8] на примере течения в каверне с подвижной крышкой (lid-driven cavity) в присутствии сильного магнитного поля авторы рассматривают нештатные режимы работы токамака, характеризующиеся высокими значениями магнитного числа Рейнольдса. Им удалось создать численную модель, которая явно учитывает распространение постоянного магнитного поля во внешнюю среду, окружающую жидкий металл.

Близким направлением является изучение плазмоконтактирующих компонентов (Plasma-Facing Components — PFC) с жидкометаллическими элементами, например, дивертора с самовосстанавливающимся жидкометаллическим покрытием, которое защищает конструкционные элементы от экстремально высоких тепловых нагрузок [12 –14] . В [12] исследуется возможность снижения МГД-потерь давления путем подвода внешнего электрического тока для изменения результирующей силы Лоренца. Данная постановка близка к рассматриваемой в предлагаемой вниманию читателя статье из-за наличия двух компонент магнитного поля, однако отличается характером распределения плотности тока: ток подводится извне и не имеет вихревой природы как в случае индуцированных токов. В работах [13, 14] изучается влияние пространственных градиентов магнитного поля, которые также генерируют вихревые токи, однако во внимание принимаются именно пространственные, а не временные градиенты, которые по величине значительно меньше, чем в переходных процессах данной работы.

В [15, 16] обсуждаются проблемы, связанные с импульсными проявлениями природы магнитного поля, а именно его силового воздействия, вызванного резким ростом скорости движения (время нарастания скорости т « 80 мс) твердого проводника в постоянном магнитном поле. Авторы заключили, что линейная зависимость между силой Лоренца и магнитным числом Рейнольдса наблюдается только при малых значениях Re m . В [15] экспериментально подтверждается наличие переходных эффектов и влияние на силу Лоренца конечных значений Re m . Роль МГД-эффектов в этих работах не рассматривается, так как объектом изучения являются твердые тела.

Таким образом, ключевыми проблемами исследования МГД-течений под действием импульсных магнитных полей являются: отсутствие экспериментальных данных для течений в условиях быстроменяющихся полей; сложности численного моделирования, требующие решения полной системы уравнений магнитной гидродинамики; тщательная верификация используемых вычислительных кодов [8] , то есть проверка получаемых с их помощью данных на предмет соответствия проектным спецификациям и стандартам, предъявляемым к исследуемым объектам.

Цель данной работы состоит в верификации нескольких численных алгоритмов, предназначенных для моделирования МГД-течений в условиях сильных нестационарных магнитных полей, поскольку предполагается, что возникающие при этом эффекты будут оказывать заметное влияние на работу бланкетов при срыве плазмы в реакторе. Проверка кодов осуществляется путем вычислительных экспериментов на классической задаче выноса магнитного поля, впервые поставленной в работе 1982 года [17] . Задача выбрана по причине опубликованных результатов ее решения методом прямого численного моделирования (Direct Numerical Simulation — DNS) в работе [18] , в которой выявлено, что существенную роль в поведении МГД-течений играют эффекты, связанные с конечным значением магнитного числа Рейнольдса (Re m > 1) и вытеснением магнитного поля из объема проводящей жидкости.

Далее рассматриваются программные пакеты: коммерческий COMSOL Multiphysics, свободно распространяемый ANES, а также программное обеспечение с открытым исходным кодом OpenFOAM и Elmer. Сравниваются результаты, полученные с помощью указанных вычислительных инструментов, оценивается эффективность счета в каждом из них, обсуждаются особенности используемых в них численных методов и математических моделей, а также формулируются выводы об эффективности применимости пакетов для решения поставленной задачи.

• 2.    Постановка задачи

  • 2.1.    Основные физические уравнения численной модели

Полная система уравнений МГД, позволяющая описать физические процессы в проводящих жидкостях при сильных быстро меняющихся полях, включает уравнения сохранения массы (неразрывности), сохранения импульса и уравнения Максвелла. Для формулировки задачи в размерном виде закон изменения импульса удобнее записать относительно субстанциональной производной скорости (производной Лагранжа), что позволит обобщить математическое представление всех рассматриваемых в данной работе численных моделей, а особенности реализации конкретных программ изложить по отдельности.

Итак, для несжимаемой жидкости уравнения сохранения массы и баланса импульса, соответственно, имеют вид:

V• u = 0, p ^U = —V p+n V 2 u + F .

В уравнениях (1) , (2) обозначено: u — векторное распределение скорости; p — давление; ρ — плотность жидкости; n = pv — динамический коэффициент вязкости жидкости, где v — кинематический коэффициент вязкости; F — объемная сила

F = ix pG + Fem, состоящая из эквивалентной силы ixρG (где G — постоянное значение градиента давления), вызванной приложенным постоянным давлением в направлении движения потока (вдоль оси x), и силового воздействия внешнего магнитного поля на проводящую среду:

Fem = Jx B = 1([VxB]x B) = — 1- V|B|2 + 1(B-V)B. M              2MM

Силовое воздействие электромагнитного поля определяется векторными полями полной магнитной индукции B = B ₀ + b и плотности тока J :

dB + (u^V)B = (B.V)u+AV2B,

∂t

J = o(E+uxB).

Уравнение переноса магнитного поля (3) выводится из уравнений Максвелла и обобщенного закона Ома (4) . В численных моделях (3) , (4) необходимо дополнить условием:

V- B = 0.

При этом (5) описывает соленоидальность магнитного поля. Решение уравнения (3) дает возможность находить плотность тока J :

Vx B = m J .

В таком представлении задачи влияние электрического поля во внимание не принимается (а именно не учитываются токи смещения).

Введем векторный магнитный потенциал A такой, что B = Vx A и V • (Vx A) = 0 ,и далее, используя обобщенный закон Ома в форме (4) и уравнения Максвелла, для плотности электрического тока придем к соотношению вида:

J = О’

∂ A

^{+ E} e ∂t

—V ф+ u xVx A

где φ — скалярный электрический потенциал. Пренебрегая влиянием внешнего электрического поля E _e и подставляя (7) в закон Ампера (6) , получим для задачи A –φ формулировку [19 –21] :

V ( V- A ) — V 2 A = мст

— ^d A + u xVx A — V ф ∂t

V 2 ф = V-

∂ A

— + u xVx A .

∂t

Количество уравнений можно сократить если считать, что V ф = 0 или ф = const. К таким допущениям часто прибегают в задачах, в которых не требуется учитывать электропроводность стенки канала (стенка «сверхпроводящая» или изолированная) или влияние особенностей геометрии на электрический потенциал. В таком случае уравнение для векторного магнитного потенциала записывается в виде:

V ( V^ A ) —V 2 A = мо

^——+ ^{u xVx A}

Использование в формулировке задачи векторного магнитного потенциала явно накладывает условие соленоидальности поля (5) и позволяет упростить задание граничных условий для магнитного поля. Функция, описывающая численное решение дифференциального уравнения для магнитного поля, выраженного через векторный магнитный потенциал, является более гладкой по сравнению с функцией решения уравнений, сформулированных относительно магнитной индукции, особенно в областях с резкими изменениями физических свойств. Это приводит к повышению устойчивости решения системы линейных алгебраических уравнений (СЛАУ). Кроме того, данный подход в двумерной постановке задачи вместо двух компонент вектора магнитной индукции требует нахождения только одной компоненты вектора магнитного потенциала. Потенциал A определяется с точностью до градиента скалярной величины ф: A ^ A + Vф. Вследствие этого для ряда физических задач из решения уравнения (8) следует множество вариаций векторного магнитного потенциала A. В таких случаях может потребоваться отыскание в явном виде потенциала на границах или его калибровка, например, калибровка Кулона: V^ A = 0. Задача вытеснения магнитного поля при течении электропроводной жидкости в плоском МГД-канале в работе [18] сформулирована в двумерной постановке с граничными условиями, которые исключали необходимость калибровки потенциала.

• 2.2.    Физическая модель

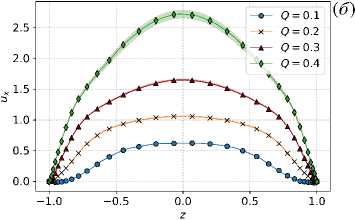
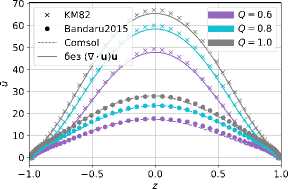
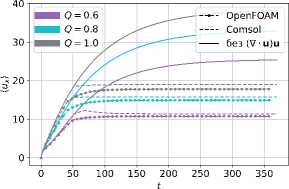
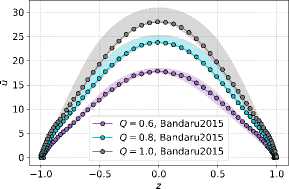
Рассматривается вынужденное течение вязкой, несжимаемой и электропроводной жидкости в плоском канале высотой 2L и длиной 2п/к под действием постоянного перепада давления и внешнего постоянного во времени магнитного поля с неоднородной поперечной компонентой B0z = B0cos(kx), где B0 — амплитуда приложенного магнитного поля, k — волновое число, [1/м]. Такие магнитные поля в реальных установках могут быть индуцированы распределенными токами в катушках с переменным сдвигом фаз в пространстве или постоянными магнитами с переменной полярностью. Постановка задачи аналогична той, которая использована авторами работы [18]. Ее схематичное представление содержит рисунок 1. Задача решается в безразмерном виде: x = x/L, z = z/L и t = t/T0, где L — линейный пространственный масштаб задачи, т0 — временной масштаб. С учетом этого высота канала составляет H = 2, а длина — Lx = 2п/(kL) = 2п/к, где к = kL — безразмерное волновое число. В начальный момент времени жидкость покоится: u(t0 = 0,x,z) = 0. Движение жидкости вызывается приложенным перепадом давления Др = 2п/к в направлении х. Как отмечено в [18], силовое воздействие вдоль канала моделируется как объемная сила Vxp = Fx = {1,0,0}, равномерно распределенная по всему объему канала.

В численных моделях авторский подход и подход в [18] эквивалентны. Однако описание перепада давления на границах в сочетании с периодическими граничными условиями для других переменных в решаемых уравнениях может привести к противоречиям в процессе вычислений. Этот момент необходимо учитывать в применяемой численной модели, а не прибегать безоговорочно к готовым типовым решениям, предлагаемым открытыми программными пакетами.

Верхняя стенка ^ ₌ q q^, ₌ q

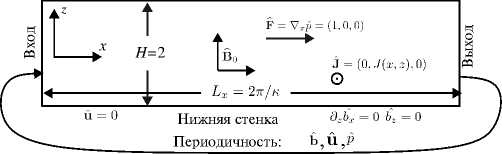
Рис. 1. Схема расчетной области и основные параметры модели

Такая проблема свойственна, например, OpenFOAM — широко известному пакету численного моделирования гидродинамических процессов.

В данной работе в постановке задачи предполагается периодичность всех физических переменных в направлении x , то есть по длине канала. На верхней и нижней стенках задается условие прилипания, согласно которым имеем: для скорости и = 0, для давления V n p = 0.

Распределение приложенного магнитного поля во всем пространстве канала в начальный момент времени в безразмерном виде опишем так:

sin(Kx)sh(Kz).    cos( kx )cH( kz) .

B (t₀ ,x,z) = B_o (x,z) =-- \  /—- i_x +--\ ?—- i_z.

^v 0, ,        ⁰⁴ ’ ’            сй(к)        x          сй(к)        z

Выражение (9) следует из аналитического решения для магнитного поля неподвижной проводящей среды при аналогичных рассматриваемым здесь геометрии и граничных условиях. При этом B = B /B ₀ , а В ₀ — масштаб для индукции магнитного поля, i x и i z — единичные векторы в направлении движения потока ( x ) и перпендикулярно стенкам канала ( z ).

В работе [18] при численном анализе задачи для скорости U ₀ , времени τ ₀ , давления P ₀ и электрического тока J 0 используются масштабы, которые определяются следующим образом:

λ           λ                       σλB 0

U0 L2k,    Т0 L2kG,    P0 PGL,    J0

На основе этих физических масштабов можно получить безразмерные формулировки уравнений для описания сохранения массы (1) , импульса (2) , эволюции магнитного поля (3) , дополненные законами Гаусса (5) и Ампера (6) :

V-u = 0, du

+ —( u -V ) u = -V p+e V ² u + F ,

∂t βκ dB 1       4 a 11

+ —(u^V)B =— B^V u+ -V2B dt вк         в кв

V^ B = 0,

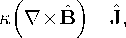
в которых u , B , J , pi — безразмерные векторные поля скорости, магнитной индукции, плотности тока и скалярное поле давлений соответственно. Силовое воздействие на поток моделируется внешней силой

F = ix + Fem = ix + 7.J x “, состоящей из постоянного градиента давления в направлении х, равного 1, и электромагнитной силы. Хотя в большинстве работ, связанных с исследованием МГД-течений, в посановках задач используются числа подобия Re, Rem и N, в данной работе для согласования обозначений с работами [17, 18] в уравнениях (10) - (14), введены безразмерные критерии, по которым и проводится верификация:

νλ	v _ 1
"   L 4 kG	U ° L = Re ’
L 4 kG P A 2	U 0 L x — Re m λ
ρL 2 kG Q = jAB 2	_ Re 1 = Ha 2 — N.

Здесь ε — о братн ое число Рейнольдса; β — магнитное число Рейнольдса; Q — обратное число Стюарта, где Ha = B 0 L у/a/(pv) — число Гартмана.

Уравнения системы (10) – (14) в самом общем случае решаются в двумерной нестационарной постановке с учетом д/ду — 0 на основе A - и B -формулировок задачи.

• 2.3.    B -формулировка

• 2.4.    A -формулировка

Уравнения системы (10)–(14) записаны для полной индукции магнитного поля, которую для удобства разложим на приложенную внешнюю (B0) и индуцируемую (Ь) составляющие: B = B0 + Ь. Это упрощает реализацию граничных условий и, по сравнению с решением для полной магнитной индукции Bˆ , снижает накопленную ошибку вычислений. Повышение точности при формулировке системы с использованием индуцируемой составляющей магнитной индукции b, а не полного поля Bˆ , объясняется структурой матрицы СЛАУ. При представлении с Bˆ некоторые члены уравнений (например, вклад внешнего поля Bˆ 0) остаются неявными и находятся численно, что вносит дополнительную погрешность. Формулировка относительно bˆ позволяет исключить известное поле Bˆ 0 из неявного оператора и вычислять соответствующие вклады явно до формирования матрицы. В результате неявная часть системы сужается, и кумулятивная ошибка уменьшается.

Итак, учитывая, что дB 0 /д1 = 0 и V 2 B 0 — 0, перепишем уравнение (12) :

!⁺вК u '   “ ° ^{+ b |} =вК ( ^[ “ ° ^{+ bbV} ) ^{u +} в ^V ’ ^b

Граничные условия на стенках при z = ± 1 для индуцируемого поля сформулируем в смешанном виде: для z-компоненты магнитной индукции b z = 0 (условие Дирихле), для х-компоненты d z b x = 0 (условие Неймана). Граничные условия b z = 0 и d zbx = 0 моделируют сверхпроводящую стенку. Первое условие (b z = 0) вытекает непосредственно из эффекта Мейснера (идеального диамагнетизма), запрещающего проникновение магнитного поля в материал. Второе условие (db x /dz = 0 — отсутствие градиента тангенциальной компоненты вдоль нормали)

обозначает, что не возникают вихревые токи и, как следствие, что поле никоим образом не проникает вглубь сверхпроводника. Такие же граничные условия используются в численных моделях МГД-течений в работах [22, 23] и полностью повторяют граничные условия модели [18] , на основе которой проводится верификация.

При записи уравнений через векторный магнитный потенциал A вместо уравнения магнитной индукции (12) получим уравнение для векторного магнитного потенциала, которое в безразмерном виде выглядит так:

+ —( u -V ) A =— (V ( b - A ) - A -V u +- V 2 A -V ( V- A ) ;

∂t βκ        βκ                  β

масштаб для векторного магнитного потенциала равен B 0 L . Тогда электромагнитная сила может быть рассчитана по формуле:

11 i

F em = Q J x “ =

К ([ VxVx A | x [ Vx A f).

Q

Отметим, что для двумерной постановки обсуждаемой задачи существует только y-проекция безразмерного магнитного векторного потенциала A = { 0, A y , 0 } ; граничные условия для него следуют из равенства n x A = n x A 0 , имеющего место на твердой границе (Z = ± 1), где y-компонента приложенного внешнего векторного магнитного потенциала .A 0 определяется из выражения B 0 = V X. A 0 иравна A y = A = (1/K)sin(Kx). Данное условие эквивалентно требованию на границе n x IB = 0 и означает отсутствие проникновения магнитного поля в стенку [22, 23] .

• 2.5.    Рассуждения о значениях размерных параметров задачи

  В [18] рассматриваются диапазон обратного числа Стюарта Q G [0.1,1.0] и значения аналогов е = 0.005 и в =1.0. Такие параметры соответствуют диапазону числа Стюарта N G [1.0,10.0], значениям гидродинамического и магнитного чисел Рейнольдса Re = 200 и Re _m = 1.0. Магнитное число Прандтля в этом случае составляет P m = v/A = Re m /Re = 0.005. Отметим, что значение P m , например, в жидких металлах на три порядка меньше. Принятое здесь такое высокое P m теоретически может отвечать сильно ионизированной плазме. Заметим также, что гидродинамическое число Re, определенное в данной задаче по масштабу скорости U ₀ , согласуется с числом Рейнольдса Re * = Re/ (3е) = 13333, вычисленным по среднерасходной скорости ( U ) = 1/ (3е) и, вообще говоря, характерно для турбулентного течения в канале, для которого использование при моделировании двумерной постановки не вполне корректно. Тем не менее результаты стационарных решений для одномерного и двумерного приближений (см. далее в разделе 3) вполне могут быть применимы к жидкометаллическим средам при условии в <<  Q.

Большинство существующих программных пакетов численного моделирования предполагают размерные формулировки физических уравнений. Одна из возможностей применения в них безразмерных уравнений заключается во введении таких значений «псевдофизических» свойств жидкости, при которых уравнения в размерной форме по виду совпадут с безразмерными. Например, для определения безразмерного числа β = 1, соответствующего магнитному числу Рейнольдса Re m = 1, удобно использовать выражение σ = Re m /(U 0 Lµ) со значением абсолютной магнитной проницаемости µ = 1 Гн/м. В этом случае электропроводность составляет σ = 1 См/м для всего рассматриваемого диапазона Q. Такой подход часто применяется в оптике, геофизике и астрофизике [24] , а также в тестовых задачах кода, в частности, в тестах OpenFOAM на задаче Гартмана [25] .

Значение Q в размерных моделях можно варьировать двумя способами: изменять или плотность ρ согласно выражению

ρ=B 0² Lσ/(NU 0 )                                        (17)

при фиксированном в (17) значении B 0 = 1 Тл, или магнитную индукцию

B 0 =  ρNU 0 /(Lσ)

при фиксированной в (18) плотности ρ = 1 кг/м ³ . Для ε = 0.005 или обратного ему значения числа Рейнольдса Re= 200 кинематическая вязкость равняется ν= U ₀ L/Re = 0.005 м ² /с для всего рассматриваемого диапазона Q при масштабе скорости U 0 = 1 м/c.

Таблица 1. К сравнению расчетных параметров в диапазоне значений Q 6 [0.1,1] при двух разных ^

Q	^ = 1, Гн/м		^ = 4п х 10 7 ,Гн/м		N	Ha
	ρ, кг/м 3	B 0 ,Тл	ρ, кг/м 3	B 0 , мТл
0.1	0.1	3.16	79577.5	3.5	10.00	44.7
0.2	0.2	2.24	159154.9	2.5	5.00	31.6
0.3	0.3	1.83	238732.4	2.0	3.30	25.8
0.4	0.4	1.58	318309.9	1.8	2.50	22.4
0.5	0.5	1.41	397887.4	1.6	2.00	20.0
0.6	0.6	1.29	477464.8	1.5	1.67	18.6
0.8	0.8	1.12	636619.8	1.2	1.25	15.8
1.0	1.0	1.00	795774.7	1.1	1.00	14.1

Другой путь прихода к безразмерным уравнениям заключается в том, что при исходных безразмерных критериях (например, ε, Q, β, κ) математической постановке задачи придается «размерная» форма со значениями, выраженными в системе СИ, а затем, после проведения расчета, решение обратно переводится в безразмерный вид. Этот прием является более предпочтительным ввиду возможных особенностей внутренней архитектуры вычислительных пакетов. Например, в COMSOL, ANSYS и Elmer по умолчанию используется значение магнитной постоянной вакуума [j,0 =4п x 10-7 Гн/м, и задать «псевдосвойство» ^ =1 Гн/м, проблематично. При том же масштабе скорости U0 = 1 м/c и ^ = 4п x 10

⁷ Гн/м

электропроводность будет равняться а = 7.958 • 10 5 См/м. В таблице 1 представлены вычисленные значения параметров для выбранного в задаче диапазона значений Q и величины соответствующих чисел Стюарта N и Гартмана Ha и двух значений абсолютной магнитной проницаемости µ. Плотность ρ вычислялась согласно (17) при фиксированном B 0 = 1 Тл, а B 0 — по (18) при постоянной плотности ρ= 1 кг/м ³ .

• 2.6.    Явление вытеснения/выноса поля

• 3.    Одномерное приближение

Перераспределение магнитного поля движущейся в нем проводящей средой — это фундаментальный МГД-процесс, который определяется конкуренцией двух эффектов, описываемых уравнением магнитной индукции:

— = Vx ( u x B )+n V 2 B .

Первое слагаемое в правой части — адвективное, изображает математически, как силовые линии магнитного поля переносятся и деформируются потоком среды, движущимся со скоростью u . В средах с высокой электропроводностью этот член доминирует и приводит к условию «вмороженности» силовых линий: они увлекаются потоком. Второе слагаемое — диффузионное, представляет естественное сопротивление магнитного поля противостоять деформации и сглаживать резкие градиенты путем диффузии. Соотношение адвективных и диффузионных эффектов характеризуется магнитным числом Рейнольдса Re m .

Явление выноса магнитного поля — один из ключевых объектов исследования в области МГД-динамо. На его основе объясняется самогенерация магнитных полей в планетах, звездах и галактиках. В работах по теории динамо [26 –29] изучается растяжение, скручивание и усиление линий магнитного поля за счет движения проводящей среды вопреки наличию омической диссипации. Задача, используемая для верификации численных моделей в данной статье, предполагает рассмотрение взаимодействия внешнего (приложенного) магнитного поля с движущейся проводящей средой, поэтому учет самогенерации магнитного поля не требуется. Тем не менее, исследуемые механизмы переноса и перераспределения магнитного поля в ограниченной геометрии актуальны как для инженерных приложений, так и для теории динамо в приложении к ограниченным областям. Стоит отметить, что течение в канале принципиально отличается от динамики планетарного или звездного динамо. Тестируемые в этой статье программы не находят широкого применения из-за особенностей реализации численных методов в исследованиях МГД-динамо. Например, в [29] авторы при изучении выноса поля в течениях с замкнутыми линиями тока прибегают к собственному псевдоспектральному методу.

В режиме Re m >  1, который рассматривается в данной работе, преобладает адвекция магнитного поля. При определенных условиях, поток жидкости может «вытеснять/выносить» магнитное поле из областей, в которых имеет высокую скорость, и концентрировать его в областях с более низкой своей скоростью. Для несжимаемой жидкости этот процесс обусловливается растяжением и в уравнении индукции (3) описывается членом ( B -V ) u . Данный эффект наиболее выражен в областях с большим градиентами скорости, например, в пограничных слоях вблизи стенок канала. Обсуждаемая здесь задача в значительной степени отличается от классического течения Гартмана, когда однородное магнитное поле приложено перпендикулярно потоку в канале [30, 31] . Скорость потока имеет только одну компоненту (допустим, u x ) , ау приложенного ортогонально потоку жидкости равномерного поля (например, B z ) индуцируется также одна компонента, направленная исключительно вдоль потока (b x ). Поскольку индуцированное поле ортогонально приложенному, они не компенсируют друг друга, и эффект вытеснения в канонической задаче течения Гартмана отсутствует.

В данной статье как приложенное, так и индуцированное магнитное поле являются неоднородными по двум компонентам. Индуцированное магнитное поле b компенсирует приложенное поле B 0 , что приводит к вытеснению полного магнитного поля B в области с наибольшими значениями градиента скорости жидкости в потоке (вблизи стенок). Под воздействием таких магнитных полей формируются существенно отличающиеся от течения Гартмана потоки, которые могут включать например, обратные течения. Такая формулировка задачи выбрана для сравнения результатов с существующими работами [17, 18] .

Следуя рассуждениям работы [17] , при условии в ^ Q и пренебрежении нелинейными членами в уравнении (11) обоснуем двумерное стационарное приближение для системы уравнений (10) , (11) , (13) , (14) и (16) в A -формулировке. Система уравнений имеет следующий безразмерный вид (символ «'», указывающий на безразмерность величин, далее в тексте опускается):

— е

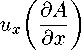
∂ ² u x ∂z ²

д ² А д ² А \

∂x ² ∂z ^{2 ,}

кдА ( д ² А д ² A \

Q ∂x ∂x ² ∂z ^{2 ,}

где A — y-проекция безразмерного магнитного векторного потенциала. Для системы (19) , (20) имеют место граничные условия, соответственно, периодические для u x и A в направлении х, а на стенке (при z = ± 1) u x = 0 и дА/дх = — cos( kx ) .

Магнитный потенциал предлагается искать в виде функции: A(x,z) = (1/K)Re iff (z)e^{t K} x) , где i — мнимая единица. Подстановка этого выражения потенциала в уравнения (19) и (20) , а также использование осреднения по x (в направлении течения) дают систему уравнений в одномерном приближении относительно u x и комплексной функции f :

— ux!m(f )=Re

d 2 f dz ²

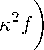
U x Re(f )=Im

d 2 f dz ²

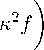
d ² u x

^£ dz ² =

u | f | ² , 2Q x f ¹ ,

и граничные условия при z = ± 1: u x = 0 и f =1.

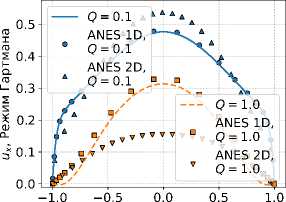
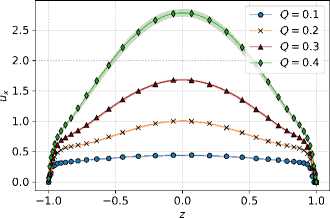
• 3.1.    Режим течения Гартмана ( Q ^ 1 )

В случае Q — 0 (Ha ч то) поток тормозится во всей области, то есть U — 0. Левые части уравнений (21) и (22) становятся близкими нулю, следовательно, поток не влияет на магнитное поле. Учтем граничные условия для f, а это означает, что Re(f) = ch(Kz)/ch(K и Im(f) = 0. Тогда, после подстановки решения для f в (23), придем к уравнению для cкорости d2ux      1    /ch(Kz)V dz2      2Q x у ch(K) )

при условиях на границе z = ± 1: u x = 0.

Одно из асимптотических приближений уравнения (1) вблизи стенки (z — ± 1) дает решение в виде течения в гартмановских слоях с характерным размером порядка 5 _Ha ~ (2е) ^{1 / 2} :

u x (z — ± 1) = 2Q 1 -

ch [ (2Qe) ^{1 / 2} z ] ch [ (2Q_e) ^{- 1 / 2} ]

Другое асимптотическое приближение уравнения (1) получается, если пренебречь трением вдали от стенки d2ux

(e— —— 0 при z — 0): dz ²

u x (z —— 0) — 2Q

/ ch(K)

у ch(Kz)

Таким образом, приближенное решение представляется как ux (z)« 2Q

ch(K ch(Kz)

ch [ (2Qe) ^{1 / 2} z ] ch ^[ (2Q_£) ^{- 1 / 2 ]}

3.2. Режим течения Пуазейля ( Q ^ 1 )

При значениях Q — то (Ha — 0) задача (1) вырождается в известное в гидродинамике течение Пуазейля в канале в отсутствие магнитного поля. Ее решением является поле скорости, выражающееся параболической зависимостью: u x (z) = (1 / 2е) (1 — z²) .В работе [17] сделано аналитическое уточнение этого решения для больших, но конечных значений Q. При выводе авторы пренебрегли диффузией f в продольном направлении течения и использовали в уравнениях (21) и (22) выражение параболического поля скорости. В итоге для f было получено

дифференциальное уравнение Эйри

d 2 f dζ ²

- iζf

при граничных условиях f (Z = 0) = 1 и f (Z — то ) = 0, где Z = е ^{1 / 3} (1 — z). Решение уравнения (25) имеет вид:

f (Z ) =

Ai(Ze ^{- in/} 6 )

Ai (0)

∞ где Ai(w) = — J^eit /3+^t)dt — функция Эйри. Окончательное выражение приближенного решения для поля скорости выглядит так:

^u x ^{( z )} ~ 2е ( 1 ^z 2 ^ + _eQ^u 1 ,

где u ^{1 ( Z} ) = - 2A

∞ ζ

Z У Z i | Ai(Z i e ^- i^n/ 6 ) | ² dZ i + / Z i² | Ai(Z i e - i^{n/ 6} ) | ² dZ i

ζ 0

, ζ ₁ — переменная интегрирования.

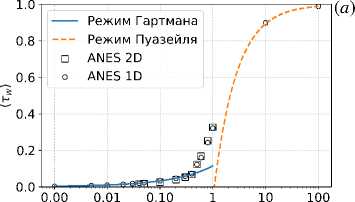
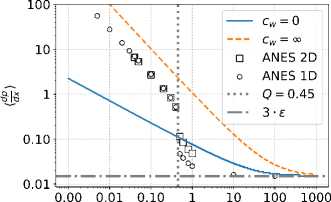
• 3.3.    Гидравлическое сопротивление

Для оценки гидравлического сопротивления рассматриваемого течения запишем одномерное нестационарное уравнение баланса импульса, которое получим интегрированием уравнения (11) для продольной скорости u _x по сечению канала S :

^Р К ^ + ' ¥ = - ¹ К > - / Tw dn C / F x dS,

S S ∂t ∂x        S S ∂x Π Π      S S где П — периметр твердых стенок канала, tw = pv(dux/dz)\w — касательные напряжения на стенке. Для стационарного (квазистационарного) установившегося потока уравнение можно упростить:

( ' ) = -Tw> П + =   T + , dx        S          L где величины в скобках ⟨...⟩ здесь и далее обозначают осреднение по длине канала согласно формуле: Lx

< g > = L _x - 1y gdx. Итак, {dp/dx), {t_w > , < F _x > — соответственно, средние величины градиента давления, 0

касательного напряжения на стенке, x -проекции электромагнитной силы. Для касательных напряжений, определяющих сопротивление трению, обычно используется соотношение:

< T w >  = ^£P < U > 2 = C f P < U > 2 ,

8           2

здесь £ = C f /4, где C f — коэффициент сопротивления трению, < U > — среднерасходная скорость потока. При переходе к безразмерному виду и учете периодических граничных условий вдоль x левая часть уравнения (1) становится равной ( — 1), тогда:

.                 1 , ^ .

1 = < ^T w >^—^< ^F x > .

Q

С практической точки зрения интерес представляют значение коэффициента сопротивления трению ( C f ) и полное гидравлическое сопротивление dp/dx , которые в обсуждаемой задаче зависят от безразмерных параметров ε , Q , β , κ .

• 4.    Настройка программных продуктов с учетом разработанных формулировок задачи

• 4.1.    Особенности формулировок в OpenFOAM

Далее проанализируем численную реализацию задачи вытеснения магнитного поля при течении электропроводной жидкости в плоском МГД-канале с помощью как открытых (OpenFOAM, ANES, Elmer), так и коммерческих (COMSOL Multiphysics) программ. В программах реализованы численные модели в A -и B -формулировках задачи распределения магнитного поля. Дискретные аналоги разрешающих уравнений имеют существенные отличия, так как получаются на основе различных численных процедур (МКО или МКЭ). Математические подходы к решению образующихся СЛАУ также отличаются.

Консервативная дифференциальная форма уравнения изменения импульса du +V • (uu) = —Vpk + v V2 u+ F                           (27)

∂t                           ρ используется в OpenFOAM для моделирования течений несжимаемых жидкостей. Уравнение (27) выражается через кинематическое давление pk = p/p и решается численно. Блок-схема основных вычислительных процедур приведена на рисунке 2.

В реализации программного кода OpenFOAM уравнение (27) представляется через потоки ϕ u на гранях ячеек и не содержит член -∇ p k :

du+V • (^u) = v V2u + F.(28)

∂tρ

Давление учитывается как поправка к импульсу в уравнении (28) , и за счет этого обеспечивается выполнение закона сохранения массы (1) . Давление определяется из решения уравнения Пуассона:

V2pk = —V[(u^V)u].

В OpenFOAM осуществляется совместное решение уравнений для полей скорости и давления на основе PIMPLE-алгоритма (Pressure–IMplicit with Pressure-Linking Equations) [4, 25, 32]. В этом алгоритме число расчетных итераций уравнения (28) имеет значение nPIMPLE на каждом временном шаге. Будем называть этот цикл «PIMPLE-контур», а итерации этого цикла — «PIMPLE-итерациями». На каждой PIMPLE-итерации производится nPISO итераций расчета давления согласно (29) в цикле под названием PISO (Pressure– Implicit with Splitting of Operators). Количество исполненных итераций решения уравнения изменения импульса может быть меньше заданного nPIMPLE при условии достижения невязкой по давлению и скорости значения, меньшего 10-4. При необходимости или по желанию уравнение изменения импульса (28) можно решать численно с явным членом давления Vpi-1 (со значением с предыдущей итерации) на каждой PIMPLE-итерации при задании переменной momentPredictor = True. Последовательность выполнения данной процедуры показана на рисунке 2.

Расчет магнитной индукции согласно уравнению (15) производится после окончания работы PIMPLE-цикла. Для этого по аналогии с процедурами реализации гидродинамической части численной модели организуется BPISO-контур (PISO-контур относительно магнитного поля — модификация классического PISO-алгоритма). Уравнение (15) решается n BPISO раз или до достижения невязкой значения 10 ^-5 по каждой компоненте магнитной индукции. На всех BPISO-итерациях магнитная индукция корректируется согласно выражению (5) n B раз. Отметим, что верхние индексы со значением (i — 1) на блок-схеме рисунка 2 обозначают явное задание данного члена в системе уравнений.

В результате проведенного параметрического исследования

Инициализация настроек модели

Временной контур

PIMPLE контур

^ + (Vu) u = W2u + F1

if momentPredictor = True:

^PIMPLE

^ + (Vu) u = z/V²u + F’^ - Vp'-

PISO контур

Р²р = -V ■ [(u ■ V) u]

корректировка поля скорости

BPISO контур

KBPISO

> + > +(Vu)b + {(Vu)B0r1

= {(VB)u}'-1 - — V2b- {—V2B0}'-’

<7 /io           O’ Hq

=V-(V-B)

корректировка магнитного поля

Запись результатов

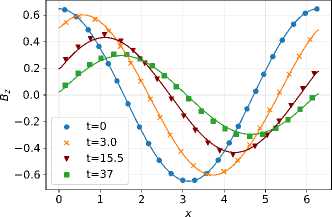
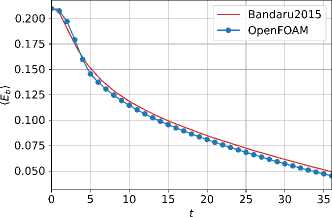
Рис. 2. Блок-схема процедур вычислительного модуля в OpenFOAM

установлены оптимальные значения итерационных параметров численной модели. Таким образом, требуется произвести n PIMPLE = n _BPISO = 4 внешних PIMPLE- и BPISO-итераций и совершить n _PISO = n _B = 2 внутренних итераций PISO и магнитных подшагов корректировки. Данная конфигурация обеспечивает баланс между точностью

решения (достаточным для достижения сходимости числом итераций) и вычислительной эффективностью (минимально необходимым числом шагов).

• 4.2.    Особенности формулировок в ANES

• 4.3.    Особенности формулировок в Elmer-FEM и Comsol Multiphysics

В ANES для построения дискретных аналогов уравнений, математически описывающих исследуемый физический процесс, используется МКО [33] в программном исполнении на языке Fortran и MPI-распараллеливание вычислений. Численно на структурных и неструктурных сетках, дискретизирущих расчетную область, решаются уравнения баланса (переноса) удельной (отнесенной к единице массы) величины Φ в обобщенной дивергентной форме:

д(дФ)+ V

Процедура решения получающихся СЛАУ аналогична описанной для пакета OpenFOAM (см. Рис. 2). Отметим, что в ANES установлен критерий сходимости по невязке 10^-5для всех Ф-переменных, поэтому на одном шаге по времени требуется большее количество итераций. Параметры PIMPLE-алгоритма при этом специально не оптимизируются под решаемую задачу и в данной работе по умолчанию принимаются следующими: n_PIMPLE= 20 и nPISO = 1.

Elmer-FEM — конечно-элементная программа с открытым исходным кодом, написанная на языке Fortran и имеющая в своей основе процедуру мультифизического моделирования и распараллеливание по MPI стандарту [36]. Comsol Multiphtsics — коммерческая, также главным образом конечно-элементная программа, ориентированная на задачи с мультифизическими процессами. Оба продукта используют конвективную форму записи уравнения изменения импульса (2):

∂u

p —+ (u-V)u = -Vp+nV^ K+F, ∂t где K = (V • u +(V'u)Tj — линеаризованный тензор скоростей деформации. В пакете Elmer-FEM нелинейное слагаемое в уравнении (30) приводится к линейному виду на первых итерациях посредством выражения (u^V)u и(U^V)u, так как оно обладает более плавной сходимостью, а на последующих — согласно формуле (u^V)uи(U^V)u + (u^V)U — (U^V)U, где U — поле скорости жидкости с предыдущей итерации.

В данной работе расчет магнитного поля с использованием модели на основе A-формулировки (16) реализован в обоих пакетах, а модели с B-формулировкой (15) — только в Elmer-FEM.

• 4.4.    Обобщение разработанных численных моделей

• 5.    Результаты

• 5.1.    Сравнение с одномерным приближением

Использованные в работе вычислительные инструменты представлены в таблице 2. Они включают шесть разработанных авторами численных моделей: по одной модели встроено в OpenFOAM и COMSOL, соответственно, на основе B- и A-формулировок, по две модели (для обеих формулировок) реализовано в ANES и Elmer. Каждая модель имеет свои особенности при расчете гидродинамики и в процедурах решения дифференциальных уравнений в частных производных. СЛАУ — результат дискретизации при помощи МКЭ, в COMSOL и Elmer решаются прямыми методами, а в ANES их метод решения является итерационным (применяется KIVA — итерационный алгоритм решения СЛАУ в матричном виде [37]) с предобуславливанием ILU, то есть с преобразованием исходной СЛАУ к виду с улучшенной обусловленностью матрицы. Предобуславливание повышает эффективность итерационных методов решения. В OpenFOAM уравнение, описывающее поле давлений, решается также итерационно — методом GAMG (Geometric Algebraic Multi-Grid) с предобуславливателем Гаусса– Зейделя [38], а уравнения для поля скорости и магнитной индукции рассчитываются с помощью встроенного в стандартную библиотеку OpenFOAM алгоритма smoothSolver для итерационного решения СЛАУ с симметричным предобуславливанием Гаусса–Зейделя [38].

Таблица 2. Используемые для численного моделирования средства

	OpenFOAM	COMSOL	ANES	Elmer
А-формулировка	–	+	+	+
В-формулировка	+	–	+	+
Постановка 1D	–	–	+	–
Постановка 2D	+	+	+	+
Метод дискретизации	МКО	МКЭ	МКО	МКЭ
Порядок аппроксимации по времени	2	2	2	2
Порядок аппроксимации по пространству	1	1	1	1
Метод решения СЛАУ	p: GAMG + GaussSeidel u,b: smoothSolver + symGaussSeidel	MUMPS	KIVA	MUMPS

Моделирование проведено при значениях в = 1, к =1, е = 0.005 и варьировании параметра Q. В расчетах с одномерным стационарным приближением (21), (22) и (23), выполненных в A-формулировке в коде ANES, параметр Q изменялся от 0.001 до 100. При вычислениях в двумерной постановке Q принимал значения из диапазона от 0.1 до 1.0 во всех кодах (см. Табл. 2). В численных алгоритмах, кроме пакета Elmer, при решении дифференциальных уравнений использовался адаптивный временной шаг, который рассчитывался на основе критерия Куранта. Все нестационарные режимы рассматривались при временном масштабе т₀= 0... 360 до момента выхода на квазистационарный режим. В решенных задачах пространственная дискретизация осуществлялась на структурной сетке с количеством элементов Nx xNz = 129 х 129, сгущающейся к стенке канала аналогично подходу, который использован в работе [18].

На рисунке 3 представлены результаты численного решения задачи в одномерной (21)–(23) и двумерной (10)–(13) постановках и аналитические приближения: (24) для поля скорости (Рис.3а) и (26) для скорости в центре канала (Рис. 3б). Видно, что в режиме Гартмана (Q = 0.1) результаты расчета поля скорости в одномерной постановке мало отличаются от аналитических приближений. Отклонения наблюдаются лишь в центральной части канала из-за пренебрежения трением в этой области в аналитическом приближении (24). Результаты вычислений в одномерной постановке и данные аналитического приближения в режиме Пуазейля (Q = 1.0) различаются значительнее. Возможно, на решение для поля скорости влияет пренебрежение диффузией магнитного поля в продольном направлении, а также использование аппроксимации в уравнении для f (26) только линейных членов. Графики, полученные в двумерной постановке, как в режиме Гартмана, так и в режиме Пуазейля показывают еще более серьезное расхождение между найденным численно и рассчитанным аналитически полем скорости практически по всему поперечному сечению канала. Исключение составляет область вблизи стенки. Зависимость скорости в центре канала от параметра Q (Рис.3б) демонстрирует существенные отклонения данных расчетов в одно- и двумерных постановках как друг от друга, так и от аналитических приближений в области развитого нестационарного течения (Q > 0.4). Отметим, что результаты в двумерной постановке являются осреднением полей вдоль оси x в стационарном случае (при Q ⩽ 0.4) и дополнительно осредняются по времени в нестационарной задаче (при Q > 0.4).

(а)

100 K =;

80 m

О

60 c s

40 Ф

20 3S

0.00   0.01    0.10     1      10     100

--- Режим Гартмана

Режим Пуа:

ANES 2D

ANES ID

136ЙЛЯ

□

Q

(б)

Рис. 3. Поля скорости (a), скорости в центре канала (б) в одно- (24) и двумерной (26) постановках и аналитические приближения

Вид распределения касательных напряжений трения на стенке показан на рисунке 4а. Видно, что аналитическое приближение (24) для режима Гартмана (сплошная линия) неплохо совпадает с результатами расчетов как в одномерном, так и в двумерном приближениях, что подтверждает адекватность разработанных моделей и, следовательно, точное описание градиента скорости (см. Рис.3а для Q = 0.1). Для режима Пуазейля ситуация несколько хуже: удовлетворительное согласование численных результатов и аналитического приближения достигается лишь при Q ⩾ 10. Как и при оценке скоростей, поля напряжений в двумерной постановке осредняются: в стационарной случае (при Q ⩽ 0.4) вдоль оси x, в нестационарной задаче (при Q > 0.4) — дополнительно по времени.

Q

Q

Рис. 4. Сопротивление трению (a) и полное сопротивление (б) в канале как функции параметра Q; сплошной и пунктирной линиями на фрагменте (б) показано полное сопротивление в задаче Гартмана [39] с изолированными (непроводящими) и сверхпроводящими стенками

Результаты для полного гидравлического сопротивления, масштабированные на среднерасходную скорость ⟨U⟩ = 1/(3ε), показаны на рисунке 4б. Здесь же, для сравнения, представлены зависимости гидравлического сопротивления в задаче Гартмана об одномерном течении в плоском канале с изолированными (∼ Ha/Re) и сверхпроводящими (∼ Ha²/Re) стенками при действии поперечного магнитного поля [39]. В режиме Гартмана (Q < Q_c∼ 0.45) полное сопротивление с увеличением Q (уменьшением числа Ha) снижается в одно- и двумерных расчетах, но хорошо совпадает в них само с собой и лежит между кривыми сопротивления из задачи Гартмана [39]. При переходе к режиму Пуазейля наблюдается кризис сопротивления — оно резко падает в окрестности Qc и при дальнейшем нарастании Q становится меньше и стремится к величине 3ε, соответствующей сопротивлению трению при ламинарном течении Пуазейля в канале в отсутствие магнитного поля. При Q > Qc ∼ 0.45 данные расчетов в одно- и двумерной постановке уже значительно различаются между собой.

• 5.2.    Обсуждение результатов, полученных с помощью различных кодов. Режим течения Гартмана

На рисунке 5 изображен установившийся профиль продольной составляющей скорости ux , полученный с помощью используемых программных пакетов. Корректность профиля можно оценить по приведенным здесь

Рис. 5. Установившийся профиль продольной составляющей скорости ux при различных значениях параметра Q, построенный в сечениях x = π (а) и x = π/2 (б); точками показаны результаты из [18], прозрачная область заливки соответствует максимальным и минимальным рассчитанным значениям

же данным из работы [18]. Видно, что с увеличением параметра Q (то есть, с уменьшением числа Стюарта) растет не только средняя скорость в канале, но и расхождение между результатами. Это связано с тем, что нелинейный член в уравнении движения становится более значимым, и, следовательно, требуется корректное (удовлетворяющее критерию Куранта) описание гидродинамики процесса. Из таблицы 3 следует, что наибольшая погрешность наблюдается при дискретизации на основе МКО, причем как в B-формулировке (OpenFOAM), так и в A-формулировке (см. пакет ANES). Это может быть вызвано большей чувствительностью в МКО-решении к величине временного шага.

Таблица 3. Максимальные отклонения данных численных расчетов от данных из [18]

OpenFOAM		COMSOL	ANES-A	ANES-B	Elmer-B
		Линия x	=π/2
Q=0.1	0.014	0.010	0.009	0.010	0.010
Q=0.2	0.016	0.008	0.008	0.010	0.009
Q=0.3	0.024	0.012	0.013	0.012	0.012
Q=0.4	0.072	0.027	0.075	0.025	0.023
Линия x = π
Q=0.1	0.014	0.018	0.018	0.018	0.018
Q=0.2	0.014	0.017	0.018	0.017	0.018
Q=0.3	0.016	0.016	0.029	0.013	0.014
Q=0.4	0.060	0.024	0.092	0.018	0.021

5.3. Верификация численных моделей в режиме Пуазейля

Переход течения проводящей жидкости из режима Гартмана в режим Пуазейля является следствием эффекта выноса магнитного поля. При больших значениях параметра Q уменьшается интенсивность силового воздействия магнитного поля на жидкость. Под действием гидравлического давления поток ускоряется, и перенос магнитного поля течением вдоль канала становится более интенсивным. Это проявляется в том, что линии магнитного поля отклоняются от центральной области канала, группируются у его стенок, формируются их новые замыкания. Влияние силы Лоренца в центре канала становится пренебрежимо малым по сравнению с силами гидравлического давления, что в свою очередь вызывает ускорение потока в этой области. На рисунке 6 представлены профили скорости для режима Пуазейля. При этом время перехода к развитому потоку в режиме Пуазейля tp слабо зависит от значения Q и в большей степени определяется точностью решения по применяемой численной модели на каждом временном шаге. Характерное время установления режима Пуазейля составляет порядка 50τ0 временных

Рис. 6. Усредненные во времени профили скорости u¯ в центре канала (расчетные и данные из работ [17] и [18]) (а); среднерасходная скорость ⟨ux⟩ как функция времени (б); профили скорости u¯ с нанесенными диапазонами отклонений от данных из работы [18] (в)

масштабов (см. Рис. 6б), что соответствует 50 с. Точность вычисления времени tp зависит от корректности разрешения уравнений поля на каждом временном шаге, особенно, если в используемом алгоритме шаг по времени адаптивный, как, например, в PIMPLE. Важно контролировать невязки получаемых физических полей во избежание потребности в искусственном изменении времени перехода tp . В данной работе невязки у всех полей не превышали 10-4, что обеспечило достаточную точность расчетов.

Рисунок 6а показывает усредненные во времени профили скорости течения электропроводной жидкости в плоском МГД-канале, вычисленные в пакете COMSOL Multiphysics для двух вариантов моделирования: с учетом нелинейного члена (V-u)u в уравнении импульса (30) (величины на рисунке обозначены согласно документации Comsol) и без его учета. Для сравнения приведены данные из работ Камкара [17] и Бандару [18] (см. кривые KM82 иBandaru2015) для значений Q = 0.6,0.8,1.0. Усреднение скорости выполнено по формуле:

1 ^u=1oT0

t_s+10τ₀

где ts ^ 50т₀ — момент выхода течения на режим Пуазейля. Интегрирование проведено на интервале десяти временных масштабов (10т₀).

Выяснилось, что при исключении нелинейного члена значения скорости существенно завышаются и

приближаются к результатам [17], а с учетом нелинейного члена скорости снижаются и согласуются с данными

[18]. Как отмечают авторы [18], отсутствие нелинейного члена в одномерной модели [17] приводит к значительным погрешностям в режиме Пуазейля. Интересно, что аналогичные работе [17] данные дают МКЭ-модели (COMSOL, Elmer) с учетом нелинейного члена, когда временной шаг превышает ограничение числа Куранта C < 1. Однако в

МКО-моделях нарушение условия Куранта неизбежно приводит к расходимости решения.

Сравнительный анализ временной эволюции средней скорости потока выявил систематическое завышение значений, отвечающих модели COMSOL Multiphysics, по сравнению с OpenFOAM, но не превышающее 5%. Для комплексной оценки точности разработанных численных моделей на рисунке 6в представлены профили скорости ux в сечении x = п, закрашенная область отражает отклонения между максимальными и минимальными значениями, полученными с помощью численных моделей и пакетов OpenFOAM, COMSOL и ANES. Наблюдается незначительное увеличение разброса площади доверительной области с ростом параметра Q. Максимальные

Таблица 4. Максимальные отклонения значений ux , рассчитанных в Comsol, OpenFOAM и ANES для Q = {0.6,0.8,1.0}

Q	OpenFOAM	Comsol	ANES
0.6	0.998	1.284	1.33
0.8	0.640	0.838	2.73
1.0	0.606	0.949	4.741

отклонения модельных данных от значений Бандару представлены в таблице 4. Стоит отметить, что наиболее

близкие к результатам Бандару значения показывает модель OpenFOAM, хотя при гартмановских режимах наиболее близкое соответствие данным Бандару демонстрирует модель ANES.

Количественная оценка воспроизводимости магнитного поля численными моделями выполнена путем сравнения распределения магнитной индукции bz вдоль центральной линии канала, рассчитанной в OpenFOAM и взятой из работы [18], при Q = 0.5 для моментов времени t =0,3,15.5,37 с (Рис. 7а). Наблюдается хорошее

соответствие полученных результатов. Дополнительно проведена оценка поведения во времени интегрального

L

x

параметра — средней магнитной энергии вдоль канала: (EB) = L^-1

/ ⁽bx

+ b2)dx. Ее временные зависимости

(Рис. 7б) демонстрируют рост расхождения до 4% к моменту t = 37 с, что связано, вероятнее всего, с различиями в подходах к коррекции поля (5) и оцифровке данных из [18] для их использования в данной работе. Однако выявленное расхождение не будет оказывать какого-либо влияния на воспроизведение планируемых физических эффектов, для наблюдения которых разрабатывались тестируемые численные модели.

Рис. 7. К сравнению вычисленных в OpneFOAM по длине канала распределения компоненты магнитной индукции bz в разные моменты времени (а) и эволюции во времени средней магнитной энергии (б) с данными из работы [18]

• 5.4.    Производительность кодов

  Таблица 5. Время расчета в используемых пакетах, [мин]

  Пакет	\ 2 ядра \ 4 ядра \ 8 ядер
  A-формулировка
  АNES		14.5	7.5	4
  Comsol		34	25.5	20
  Elmer		48	32	21.5
  B-формулировка
  OpenFOAM		4.5	3	2
  АNES		39	20.5	11
  Elmer		510	257	126

  
  

  Сравнение производительности кодов осуществлено на вычислительной станции AMD Ryzen 9 3900X (12 ядер, 4.2 ГГц), 64 ГБ DDR4 (2666 МГц) при следующих настройках: время расчета 60 с; число итераций, приходящихся на временной шаг 10 (PIMPLE-итераций); ограничение по числу Куранта C = 0.5; шаг записи числовых данных 1 с. Результаты тестирования представлены в таблице 5. Особое внимание уделено масштабированию пакетов при различном числе ядер. Наибольшую эффективность демонстрирует OpenFOAM (при B-формулировке) с

• 6.    Заключение

временем расчета 2–4.5 мин. Среди программ с векторным магнитным потенциалом (с А-формулировкой) наиболее эффективным является пакет ANES (4–14.5 мин). Наименьший выигрыш от распараллеливания (20–34 мин) показывает COMSOL.

Следует отметить, что OpenFOAM с включением моделей может быть реализован и через векторный магнитный потенциал. При этом будет решаться СЛАУ вдвое меньшего размера и, следовательно, сократится время моделирования. Ключевой особенностью высокой производительности кодов OpenFOAM и ANES является высокая стабильность МКО-дискретизации в задачах гидродинамики, что дает высокую эффективность их решения. Отличие времени расчета по разработанным моделям в OpenFOAM (счет по программе на языке C++) и ANES (счет по программе на языке Fortran), возможно, заключается в различиях реализации и оптимизации программных алгоритмов, которые содержатся в вычислительных модулях, а также в управлении памятью центральных процессоров во время решения.

Выполнена верификация численных моделей, разработанных для воспроизведения поведения проводящих жидкостей в условиях, когда магнитное число Рейнольдса Rem ≳ 1, что характерно для процессов при наличии импульсных магнитных полей в термоядерных реакторах. Модели реализованы в четырех программных пакетах: ANES, OpenFOAM, Elmer и COMSOL Multiphysics. Тестирование показало, что пакеты, использующие для дискретизации МКО (OpenFOAM и ANES) демонстрируют наибольшую вычислительную эффективность и более высокую стабильность решения. В частности, OpenFOAM с моделью магнитного поля в B-формулировке требует меньшего вычислительного времени, чем даже модели МКЭ на основе A-формулировки, хотя последние решают в два раза меньшее число уравнений, описывающих эволюцию магнитного поля. Выявлено, однако, что МКО-модели более чувствительны к величине временного шага и требуют строгого соблюдения критерия Куранта для обеспечения сходимости решения. В то же время МКЭ-модели (COMSOL и Elmer) при нарушении этого критерия могут давать физически некорректные, но численно стабильные результаты.

Таким образом, по совокупности критериев точности и производительности для решения обсуждаемого класса задач среди протестированных программных пакетов наиболее перспективным представляется OpenFOAM. Несмотря на то, что в отдельных режимах лучшую точность демонстрируют другие пакеты (например, ANES в гартмановских режимах), меньшее время расчета и хорошая общая согласованность с данными из работы [18] делает OpenFOAM предпочтительным инструментом. Дальнейшее развитие кода, в частности, введение в вычислительный модуль модели на основе векторного магнитного потенциала (A-формулировки) поможет дополнительно сократить время вычислений и улучшить сходимость при наличии в расчетной области неоднородности свойств. Потенциально повысить производительность численных моделей, применяемых в ANES, можно за счет оптимизации настроек PIMPLE-алгоритма для решения уравнения баланса импульса.

Проведенный анализ продемонстрировал ключевую роль нелинейного члена в уравнении движения, особенно при течении в режиме Пуазейля (Q ⩾ 0.5), где его учет позволяет получить данные, близкие к результатам из [18]. Установлено, что согласно упрощенной одномерной модели (21)–(22), использующей осреднение по длине канала и не учитывающей это нелинейное слагаемое, как и из аналитических зависимостей, получаются решения для предельных случаев: Q → 0 (течение Гартмана) и Q → ∞ (течение Пуазейля). При параметре же Q > Qc ≈ 0.45 поля скорости течения значительно искажаются, что согласуется с выводами более ранних работ [17]. Построены практически значимые зависимости от параметра Q для касательных напряжений и полного гидравлического сопротивления течению. Расчеты подтверждают наличие кризиса сопротивления в области перехода от течения Гартмана к течению Пуазейля в области 0.4 < Q < 0.5, после которого при дальнейшем увеличении Q одномерные и двумерные модели дают существенно различающиеся результаты. Все это подчеркивает ограниченность одномерных подходов при рассмотрении режимов, в которых перенос магнитного поля течением электропроводной жидкости играет значимую роль.

Работа выполнена при поддержке Российского научного фонда, проект № 25-19-00642 .