Численное определение несущей способности армированных кольцевых пластин, покоящихся на несжимаемом жидком основании и по-разному сопротивляющихся растяжению и сжатию
Автор: Янковский А.П.
Журнал: Вычислительная механика сплошных сред @journal-icmm
Статья в выпуске: 2 т.18, 2025 года.
Бесплатный доступ
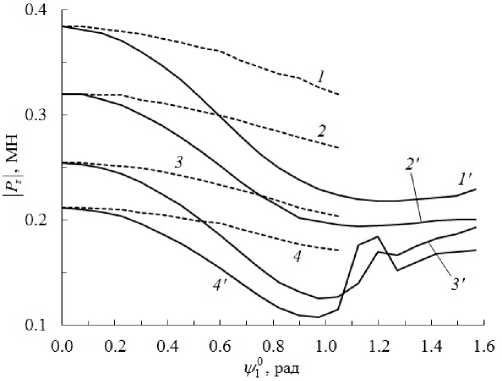
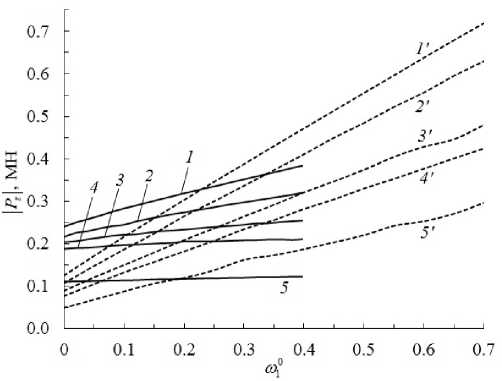
На основе принципа виртуальной мощности сформулирована экстремальная задача определения верхней (кинематической) границы несущей способности изгибаемых кольцевых армированных двухслойных пластин, контактирующих по одной из лицевых плоскостей с несжимаемой жидкостью. Присутствующие в пластинах сквозные отверстия закрыты абсолютно жесткими вставками (шайбами). Структура армирования обладает радиальной и осевой симметрией. Деформированное состояние пластин описывается кинематическими соотношениями классической теории изгиба. Использована жесткопластическая модель механического поведения материалов компонентов композиций, согласно которой пластическое течение в них ассоциируется с кусочно-линейными критериями текучести. Фазовые материалы могут иметь разные пределы текучести при растяжении и сжатии; материал связующей матрицы обладает цилиндрической ортотропией. Пластическое течение композиций происходит в рамках структурной модели, учитывающей возникновение плоского напряженного состояния во всех компонентах. Вдоль полярного радиуса произведена дискретизация поставленной осесимметричной задачи. Для ее численного решения применен симплекс-метод теории линейного программирования. На примерах деформирования однородных и изотропных пластин продемонстрирована сходимость численного решения и его хорошее согласование с результатами расчетов по ранее полученным аналитическим выражениям. Выполнен параметрический анализ влияния направлений и плотностей армирования пластин на предельно допустимую величину поперечной силы, действующей на жесткую шайбу. Рассмотрены варианты укладки волокон по прямолинейным радиально-симметричным траекториям и логарифмическим спиралям, а также радиально-окружные структуры армирования. Продемонстрировано, что наибольшая несущая способность присуща конструкции с радиально-окружной структурой при жестко защемленной внешней кромке и жестком закреплении шайбы и условии, что суммарная плотность армирования в каждой точке пластины постоянна и равна предельно допустимому (технологически) значению. Исследовано нетрадиционное граничное условие на внешней кромке пластины - ее подвижная в вертикальном направлении заделка.
Изгибаемые кольцевые пластины, армирование волокнами, жесткая вставка (шайба), несжимаемое жидкое основание, жесткопластическая модель, разносопротивляемость, кусочно-линейные критерии текучести, двуслойная модель изгиба, предельное состояние, несущая способность, численное решение, линейное программирование
Короткий адрес: https://sciup.org/143184629
IDR: 143184629 | DOI: 10.7242/1999-6691/2025.18.2.12
Текст научной статьи Численное определение несущей способности армированных кольцевых пластин, покоящихся на несжимаемом жидком основании и по-разному сопротивляющихся растяжению и сжатию
В современной инженерии широко распространены конструкции из композитных материалов (КМ) [1 –6] , компоненты которых при высокоинтенсивных нагрузках могут испытывать пластическое деформирование [1, 2, 4, 6, 7] . Поэтому актуальна проблема математического моделирования неупругого поведения КМ-изделий, которая на данный момент времени находится на стадии становления [4, 6 –18] .
Для оценки в первом приближении несущей способности КМ-конструкций целесообразно применять жесткопластическую модель деформирования компонентов их композиций [11, 19] . Согласно ей, в [10 –12, 14, 17, 18] рассматривалось механическое поведение волокнистых пластин и оболочек в их предельном состоянии. Тонкостенные КМ-конструкции используются в качестве контейнеров, заполненных жидкостью [20, 21] , а также эксплуатируются как емкости под водой, где возможен контакт с несжимаемой жидкостью. Следовательно, практический интерес представляет и определение несущей способности волокнистых пластин и оболочек, функционирующих в таких условиях. Так, в работах [12, 14] в аналитической форме построены полные решения о предельном изгибном состоянии волокнистых круглых пластин, покоящихся на несжимаемой жидкости. Авторы в [12, 14] полностью повторили ход рассуждений, который ранее использовался для однородных пластин [22, 23] . В отличие от базовой работы [22] , в [12, 14, 23] предполагалось, что материал изгибаемой пластины в предельном состоянии по-разному сопротивляется растяжению и сжатию. При этом в [12, 14, 23] исследования выполнялись в рамках теории поперечного изгиба пластин, то есть не учитывались мембранные усилия, свойственные предельному состоянию таких конструкций, что, строго говоря, справедливо только для изгибаемых пластин, материалы которых имеют одинаковые пределы текучести при растяжении и сжатии (см. [22] ). Как будет показано далее, в изгибаемых пластинах, изготовленных из разносопротивляющихся материалов, мембранными усилиями пренебрегать нельзя, поэтому аналитические решения, построенные в [12, 14, 23] при отсутствии этих усилий, следует признать некорректными.
При моделировании предельного состояния изгибаемых армированных пластин из разносопротивляющихся фазовых материалов прежде всего необходимо определить поверхность текучести их композиций, поведение которых зависит и от изгибающих моментов, и от мембранных усилий (следует заметить, что в [12, 14, 23] учитываются только изгибающие моменты, которые представляются с использованием лишь кривых текучести). Даже у однородной осесимметрично деформируемой цилиндрической оболочки из равносопротивляющегося материала поверхность текучести в четырехмерном пространстве «изгибающие моменты–мембранные усилия»
получается весьма сложной [24] . Еще большие трудности возникают в случае КМ-конструкций, в силу чего автор работы [10] вынужден был прибегнуть к упрощенной (двуслойной) модели тонкостенной оболочки. Однако даже при таком упрощении поверхность текучести у армированной изгибаемой оболочки оказалась настолько сложной, что в [10] она подгонялась под более простую поверхность, установленную ранее в [24] .
Приведенный анализ публикаций показывает, что адекватный расчет несущей способности тонкостенных КМ-конструкций, особенно из разносопротивляющихся материалов осуществим, по-видимому, только численно. Так, в [11] для отыскания верхней (кинематической) границы несущей способности однородных пластин и оболочек был предложен численный метод, вытекающий из теории линейного программирования [25] . Позже он эффективно применен для решения аналогичных задач изгиба волокнистых пластин и пологих оболочек [17] .
С учетом вышеизложенного данная работа посвящена: во-первых, численному определению верхней границы предельной нагрузки для изгибаемых круглых составных армированных пластин, покоящихся на несжимаемом жидком основании, материалы компонентов композиции которых по-разному сопротивляются растяжению и сжатию; во-вторых, верификации разработанного для этого численного метода; в-третьих, анализу влияния параметров армирования на величину предельной нагрузки.
-
2. Формулировка задачи и численный метод расчета
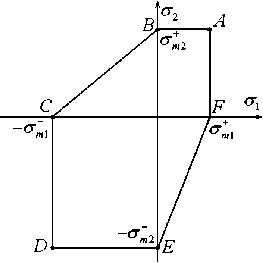
Рассмотрим тонкую кольцевую пластину, возможно, переменной толщины 2 h , ограниченную кромками радиусов R 0 и R 1 (R 0 < R 1 ). Внутреннее отверстие радиуса R 0 (Рис. 1) полностью закрыто жесткой вставкой (шайбой), которая может быть соединена с пластиной шарнирно или жестко (подвижная в вертикальном направлении заделка на внутренней кромке радиуса R 0 ). Конструкция покоится на жидком основании, причем в предельном состоянии не допускается перетекание несжимаемой жидкости с одной лицевой поверхности на другую. На внешней кромке радиуса R 1 пластина может иметь разные типы опирания: жесткое защемление или подвижное соединение, закрепленный или подвижный шарнир. В целом составная конструкция обладает осевой симметрией.
Кольцевая пластина осесимметрично усилена двумя семействами волокон с плотностями ω k и углами армирования ^ k (k = 1,2), которые отсчитываются в направлении вращения полярного радиуса r (см. Рис. 1 а , ψ 1 — угол первого семейства армирующих волокон). Сравниваются две структуры:
-
1) радиально-симметричное армирование двумя семействами волокон, изготовленных из одинакового материала и уложенных по спиральным траекториям: w 1 (r) = w 2 (r), ^ 1 (r) = —fa (r), R 0 < r < R 1 (см. Рис. 1 а , б );
-
2) армирование в радиальном (w 1 (r), fa(r) = 0) и/или окружном (w 2 (r), fa(r) = п/2) направлениях (см. Рис. 1 в ); при этом волокна разных семейств могут быть выполнены из разных материалов.
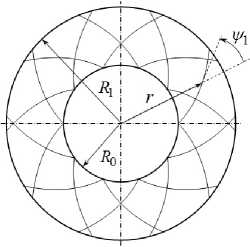
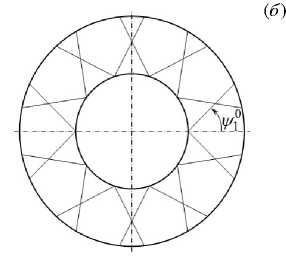
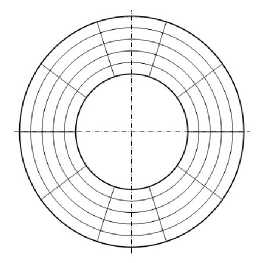
Рис. 1. Варианты армирования изгибаемой пластины: по логарифмическим спиралям ( а ); по прямолинейным радиальносимметричным траекториям ( б ); по радиальным и окружным направлениям ( в )
В поперечном направлении z ( | z | ⩽ h ) структуры армирования квазиоднородны. Армирующие волокна имеют постоянные поперечные сечения [1, 3] и обрываются только на кромках пластины, поэтому при укладке силовых элементов k -го семейства по спиральным траекториям плотности армирования определяются по формулам [17] :
w k (r) = h o R o w ° cosfa ° /[h(ryrcosfa (r)], R o < r < R i , h o = h(R o ) w k = ^ k (R o ), fa 0 = fa k (R o ), fa= n/2 (k = 1,2),
где w 0 > 0 — интенсивность армирования на кромке внутреннего отверстия радиуса R 0 . При окружной укладке волокон k-го семейства угол равен fa = fa = п/2, поэтому в правой части первого равенства из (1) возникает неопределенность 0/0, а значит, плотность армирования ω k может задаваться произвольно, но с учетом следующих физических ограничений: при любых структурах армирования функции w k (r) являются неотрицательными и суммарная плотность армирования ш % (r) удовлетворяет неравенству [17] :
w s (r) = W i (r)+W 2 (r) < w m = const < 1 (w k (r) > 0, k =1,2), R o < r < R i , (2)
где w m > 0 — максимально допустимое значение w % ; на практике оно обычно таково: w m « 0.7 [26] .
Жесткопластические материалы композиции однородны, их пределы текучести при растяжении и сжатии могут различаться. Арматура полагается изотропной, а связующая матрица обладает цилиндрической ортотропией. В предельном состоянии пластическое течение в фазах композиции ассоциировано с кусочно-линейными условиями текучести (типа модифицированных критериев Треска и Ишлинского–Ивлева [11, 17, 19, 27] ).
Конструкция осесимметрично нагружена в трансверсальном направлении z и, возможно, в радиальном — r . При указанных выше свойствах материалов субструктурных элементов композиции, особенностях армирования, геометрии, способах закрепления и нагружения в пластине, находящейся в предельном состоянии, реализуется осесимметричный изгиб, который описывается соотношениями кластической теории идеально пластических тел и конструкций [11, 28] . Согласно этому, в предельном состоянии кольцевой пластины направления главных осредненных напряжений и ассоциированных с ними скоростей деформаций в композиции совпадают с радиальным и окружным направлениями.
К рассматриваемой конструкции приложены нагрузки двух типов. Внешние силы первого типа имеют фиксированные значения (например, весовые нагрузки, а также выталкивающая сила со стороны жидкого основания — отпор жидкости в предельном состоянии [14, 22] ). Внешние силы второго типа предполагаются пропорциональными параметру нагружения p, для которого необходимо определить предельно допустимое значение (то есть минимальное).
Пусть u (r) и v (r) — кинематически допустимые скорости точек срединной плоскости пластины (z = 0) в радиальном ( r ) и поперечном ( z ) направлениях ( v — скорость прогиба); v 0 — кинематически допустимая скорость смещения жесткой шайбы вдоль оси z ; q — значение отпора жидкости, который равномерно действует на срединную плоскость всей составной конструкции (шайбы и пластины); G — фиксированный вес жесткой шайбы с учетом уложенных на ней грузов; g r (r) и g z (r) — заданные массовые нагрузки, которые действуют на единицу площади срединной поверхности КМ-пластины в направлениях r и z и выражаются так [17] :
gr(r) = 2fr(r)h(r)(^o(r)po + ^Mk (r)Pk), gz(r) = -2gh(r)(^o(r)Po + ^^k (r)Pk), k=1 k=1
w o (r) = 1 —^^k(r), R o < r < R 1 .
k =1
Здесь g = 9.81 м/с 2 ; p 0 , pk — объемная плотность материала связующей матрицы и волокон k-го семейства; ω 0 — относительное объемное содержание связующего материала в репрезентативной ячейке композиции; f r (r) — интенсивность массовой нагрузки в радиальном направлении (например, если рассматриваемая конструкция является элементом центрифуги, вращающейся вокруг вертикальной оси z с постоянной угловой скоростью ш, то f r (r) = rw 2 ).
Нефиксированные нагрузки состоят из суммарной силы P z , которая действует на шайбу в направлении оси z , и, в частности, из поперечной распределенной силы p z (r), которая действует на КМ-пластину. Эти и аналогичные им нагрузки (подробнее см. ниже) пропорциональны параметру нагружения p , то есть
P z = pP z , P z (r)= PP z (r), R o < r < R i , (4)
где P z и p z (r ) — соответственно известная величина и функция от r.
Предельно допустимое значение параметра p обозначим как p ∗ ; для его определения воспользуемся принципом виртуальной мощности [11] . В самом общем случае закрепления и нагружения рассматриваемой конструкции этот принцип с учетом соотношений (3) и (4) выражается равенством:
R 1
p [ P z v o +2nR i ( Q Z
11 v i +T r u i + mn
^ i ) +2nRom П ^ о +2n
j P z (r)v(r')rdr] =
R 0
R 1 R 1 R 1
= 2п У D(r)rdr — 2n j[g r (r)u(r)+ g z (r)v(r)]rdr-nq(v o R 2 +2^ v(r)rdr)
— Gvo — 2nR o M°'d o
R 0 R 0
R 0
—2nR i (Qi v i +T i u i + М П $1).
Здесь D — мощность диссипации механической энергии, отнесенная к единице площади срединной поверхности изгибаемой пластины; M n j — фиксированные изгибающие моменты на кромках пластины радиусов R j ; pm jn — изгибающие моменты на кромках радиусов R j (j = 0, 1), пропорциональные параметру нагружения p (аналогично выражениям (4) ); T 1 и Q 1 — фиксированные мембранное радиальное усилие и перерезывающая сила, заданные на внешней кромке r = R i, pT r и pQ \ — мембранное радиальное усилие и перерезывающая сила на кромке r = R i , пропорциональные параметру p; u i и v i — скорости радиального смещения и прогиба точек пластины на внешней кромке радиуса R 1 ; ϑ 0 и ϑ 1 — скорости поворота нормали к срединной плоскости пластины
в радиальномнаправлении накромкахрадиусов R o и R 1 , то есть d j = d(R j ) (j = 0,1), причем
d(r) = -v'(r), R 0 < r < R 1 ;
штрих означает производную по радиальной координате r . Предполагается, что при плоском напряженном состоянии (ПНС) в плоскости главных усредненных напряжений ( σ 1 и σ 2 ) кривая текучести КМ представляется кусочно-линейной [11, 19, 27] .
Условия совместного перемещения точек внутренней кромки КМ-пластины и жесткой шайбы определяются равенствами:
u(R o )=O, v o = v(R o ).
Рассматриваемая составная пластина покоится на несжимаемом жидком основании и конструктивно выполнена так, что в ее предельном состоянии жидкость не может перетекать с одной лицевой поверхности на другую, поэтому при учете второго равенства из (7) должно выполняться дополнительное соотношение [12, 14, 22, 23] :
R 1
v 0 R 2 + 2 У v(r)rdr = 0.
R 0
Согласно формулировке кинематического метода [11] , для получения верхней границы несущей способности такой конструкции из соотношения (5) нужно сначала вычислить минимальное значение p ∗ параметра нагружения p при всех кинематически допустимых распределениях функций u(r) и v(r).
Для построения численного решения задачи (5) – (8) от равенства (5) при учете (8) целесообразно перейти к задаче минимизации [11]
{ R i
2n / D(r)rdr — Gv 0 — 2nR 0 M n d 0 -
R 0
R 1
-2nR i ( Q i v i + Tu i + M ^ d i ) - 2n J[g r (r)u(r)+g z (r)v(r)]rdr
R 0
при условии нормирования
R 1
P z v o + 2nR i ( Q Z v i + T 1 u i +m П ^ i )+2nR o m ^ ^ o + 2n Jp z (r)v(r)rdr = 1
R 0
и ограничениях–неравенствах
J
D > X8:^ (n =1,2,...,N), D > 0.
j =1
Здесь S j,n — значения j -х обобщенных напряжений (например мембранных усилий или изгибающих моментов) в n -й угловой точке линеаризованной поверхности текучести изгибаемой КМ-пластины; N — число угловых точек этой поверхности; qj — значение j -й обобщенной скорости деформаций, определяемое кинематическим соотношением (подобным (6) ) через допустимые скорости перемещения точек КМ-пластины; J — количество обобщенных напряжений S j и соотносящихся с ними обобщенных скоростей деформаций q j (при рассматриваемом осесимметричном общем изгибе кольцевой пластины пространство «мембранные усилия-изгибающие моменты» имеет размерность J = 4).
Система неравенств (11) соответствует принципу максимума Мизеса [11, 19], согласно которому мощность «ассоциированных» обобщенных напряжений Sj на отвечающих им обобщенных скоростях деформаций qj (при J этом D = ^^Sjqj) больше или равна мощности любого не «ассоциированного» обобщенного напряжения Sjn j=1
на этих же скоростях q j .
Как отмечалось в разделе 1, в общем случае изгиба тонкостенных конструкций построение поверхности текучести в пространстве обобщенных напряжений Sj (например в пространстве мембранных усилий и изгибающих моментов) представляет собой довольно сложную задачу, причем получающиеся при этом поверхности текучести не являются кусочно-линейными [10, 24], поэтому-то в [10] для армированных оболочек была применена упрощенная модель деформирования — двуслойная модель изгибного поведения КМ-оболочек. Учитывая эти обстоятельства, при разработке численного метода решения возникающей в данной работе экстремальной задачи целесообразно ориентироваться сразу на двуслойную модель, без предварительного построения поверхности текучести в пространстве обобщенных напряжений Sj, j = 1,J. Возможно использование и более сложной —M-слойной — модели (M > 3). Однако, как показывают расчеты [11], с практической точки зрения уточнение верхней границы несущей способности тонкостенных конструкций при M > 3, по сравнению с M = 2, пренебрежимо мало, но создает значительные вычислительные трудности.
Согласно двуслойной модели, изгибаемая пластина рассматривается как состоящая из двух фиктивных слоев; толщина каждого слоя h(r), расстояние между срединными плоскостями слоев также h(r). Присвоим верхнему слою номер 1, а нижнему номер 2. Диссипация механической энергии в пластине D (r) (см. (9) ) равна сумме диссипаций в слоях, в которых реализуется ПНС, однородное в поперечном направлении, то есть
D(r) = Dir>(r)+Di2>(r), R0 D®(r) = h[a^(r) (^i(r)-(-1Пк1(гУ2}+^\г) (e2(r)-(-1)ihK2(r)/2)] (i = 1,2), При этом £1и £2— скорости мембранных деформаций КМ-пластины в радиальном и окружном направлениях; к1и к2 — скорости параметров искривления срединной плоскости изгибаемой кирхгофовской пластины в тех же направлениях [11, 17, 28]; ^[' и a^i —радиальное и окружное усредненные напряжения в композиции i-го слоя, которые, как уже отмечалось, являются главными напряжениями (аналогично и £1, £2, и к1, к2); верхний индекс в скобках указывает на номер слоя. В двух последних равенствах из (14) следует принимать во внимание выражение (6). Таким образом, задачу определения верхней (кинематической) границы несущей способности изгибаемой составной КМ-конструкции, покоящейся на несжимаемом жидком основании, в рамках двуслойной модели сформулируем так (см. (9) и (12)): найти минимум параметра нагрузки {Ri 2п / hD(1)(r) + D(2)(r)lrdr— Gv0—2пЕоМП$о— R0 R1 —2nRi (Qivi +Tiui +МП'&1 )—2п/ [gr(r)u(r)+gz (r)v(r)]rdr R0 при ограничениях–равенствах (7), (8), (10) и ограничениях–неравенствах (см. (11), (13) и (14) с учетом (6)) D^r) >hh где aj^ — значение напряжения aji (j = 1,2) в n-й угловой точке кусочно-линейной кривой текучести композиции при ПНС, N — количество угловых точек этой кривой (условия (16) эквивалентны неравенствам (11)). К соотношениям (7), (8), (10), (15) и (16) необходимо присоединить кинематические граничные условия на внешней кромке (см. (6)): u(Ri)= uj, v(Ri) = vj, v‘(Ri) = —^, (17) где uj, vj и dj — заданные фиксированные величины. Если КМ-пластина на ее внутренней кромке соединена с шайбой жестко, то к равенствам (7) следует добавить соотношение (подвижная заделка): v‘(Ro) = O. (18) Минимум функционала (15) с учетом ограничений–равенств (7), (8), (10), (17), (18) и ограничений–неравенств (16) будем определять численно, методами теории линейного программирования [11, 17, 25]. С этой целью предварительно дискретизируем сформулированную задачу условной минимизации: введем равномерную сетку на интервале r G [R0,R 1 ] с шагом Д =(R 1 — Ro)/(K — 1). Узлы сетки имеют координаты rk = r 1 + (k — 1)Д (при этом r1 = Ro, rK = R1, k = 1,2,...,K, где K — количество узлов). Интегралы в соотношениях (8), (10) и (15) вычислим приближенно с применением формулы трапеций. Производные в неравенствах (16), краевых условиях (17), (18) и в соотношениях (10), (15) при учете выражения (6) запишем в конечно-разностном виде. Для этого во внутренних узлах сетки (2 < k < K — 1) для аппроксимации производных от v прибегнем к центральным конечным разностям на трехточечном шаблоне {rk-1,rk ,rk+1}; в крайних же узлах r1 и rK первые производные от v в соотношениях (10), (15)–(18) (при учете (6)) заменим скошенными разностями также на трехточечных шаблонах, а вторые производные от v в неравенствах (16) — скошенными разностями, но на четырехточечных шаблонах [29]. В отличие от предыдущего, производную от u в (16) аппроксимируем скошенной, например, влево конечной разностью на трехточечном шаблоне {rk,rk+1,rk+2} при 1 < k < K — 2; в двух же последних узлах (rK-1 и rK) используем аналогичную конечную разность, но скошенную вправо [29]. Такой нетрадиционный способ дискретизации рассматриваемой экстремальной задачи позволяет построить устойчивое численное решение со 2-м порядком точности по шагу ∆. После завершения дискретизации задача поиска минимума функционала, аналогичного (15), решена симплекс-методом теории линейного программирования [25]. Найденное численное решение не является полным, так как, согласно равенству (8), соотношения (9) и (10) (а затем (10) и (15)), полученные из равенства (5), уже не содержат величину отпора жидкости q, и она остается неизвестной. Следовательно, разработанный метод не способен вычислить значение q (построенное же ранее в [22] полное аналитическое решение аналогичной задачи для однородной пластины, материал которой подчиняется условию текучести Треска, определяет величину q). Очевидно, что с точки зрения инженерных приложений интересно не конкретное значение q, а знание p∗— предельно допустимой величины параметра нагружения. Поэтому предлагаемый численный подход все-таки имеет практическую значимость. Однако с его помощью невозможно найти в узлах сетки значения усредненных напряжений a(i) (rk) и a(i) (rk) (1 < k< K) в композиции i-го слоя конструкции (см. (13)). Поэтому, согласно соотношениям (16), для реализации разработанного численного подхода необходимо предварительно рассчитать координаты угловых точек a^n и a^n (1 < n< N) на кусочно-линейных кривых текучести КМ в каждом i-м слое пластины (i =1,2). 3. Кривые текучести армированного материала пластины Для определения напряжений a^n и a^n (i = 1, 2, 1 < n< N), входящих в неравенства (16), необходимо построить кусочно-линейные кривые текучести композиции усиленной волокнами пластины. В рамках принятой двуслойной модели в каждом из фиктивных слоев КМ-конструкции приближенно реализуется ПНС. При этом, как отмечалось выше, напряжения в радиальном и окружном направлениях (и в связующей матрице, и в волокнистой композиции) являются главными для рассматриваемых структур армирования, способов нагружения и закрепления составной пластины. Так как структура армирования пластины однородна по толщине, в ее обоих слоях кривые текучести композиции одинаковы, поэтому в данном разделе далее, в отличие от (16), верхний индекс (i), обозначающий номер слоя не указываем. При условии, что кривые текучести материалов всех компонентов композиции при ПНС являются кусочно-линейными (см. Рис. 2), кривую текучести КМ можно рассчитать по формулам из работы [16]. Однако получающаяся при этом кусочно-линейная кривая текучести задается параметрически, то есть в неявном виде, что приводит к некоторым (но не принципиальным) трудностям определения координат присутствующих угловых точек. Поэтому используем упрощенный вариант структурной модели из [16], который позволяет рассчитывать координаты угловых точек на кривой текучести КМ [17]. При этом предполагаем, что связующему материалу присущи не только разные пределы текучести при растяжении и сжатии, но и цилиндрическая ортотропия. Пусть amj > 0 — пределы текучести материала связующей матрицы при растяжении (+) и сжатии (-) в радиальном (j = 1) и окружном (j = 2) направлениях, а его кусочно-линейная кривая текучести соответствует модифицированному критерию Треска при ПНС [30] (см. Рис. 2а), из которого при am. = am2 и ami = am2вытекает критерий текучести Ху для изотропного материала, имеющего разные пределы текучести при растяжении и сжатии [27], апри am. = am^ = am1= am2— критерий текучести Треска [11, 19]. (a) (в) Рис. 2. Кусочно-линейные кривые текучести КМ пластины: согласно модифицированному критерию Треска–Ху для ортотропного материала (а); при прямолинейной радиально-симметричной укладке волокон (б); при радиальноокружной структуре армирования (в) Первый тип структуры армирования (Рис. 1а, б). Обозначим через a+ и a— пределы текучести изотропной арматуры k-го семейства со при растяжении и сжатии (a±] > 0, k = 1, 2). При этом варианте армирования выполняются равенства: ^2(r) = —^1(r), w2(r) = w1(r) и a± = a± (R0< r< R1). Кривая текучести композиции при ПНС и указанных параметрах армирования, согласно [17], в общем случае представляет собой восьмиугольник ABCDEFGH (Рис. 2б), координаты a1,n и a2,n (1 < n < N = 8) угловых точек которого вычисляются по формулам: где A: B: C: D: E: F: G: H: σ1 =<1,1=<+1+<m1, <2=<2,1=<+2+<m2; σ1 = <1,2 = <+1, <2 = <2,2 = <+2 +<m2; <1 = <1,3 = -<-1, <2 = <2,3 = -<f2+<m2 (<+2/<-1 < <+2/< <1 = <1,3 = <+1 -<m1, <2 = <2,3 = <f2 (<+2/<f1 ><m2/<m1): σ1 = <1,4 = -<-1 -<m1, <2 = <2,4 = -<-2; σ1 = <1,5 = -< f1-<m1, <2 = <2,5 = -<f2 -<m2; σ1 = <1,6 = -<-1, <2 = <2,6 = —<+-2 -<m2; <1 = <1,7 = <+1, <2 = <2,7 = <+2 -<m2 (<+2/<-1 < <m2/<m1): ( J1 = <1,7 = -<f1 + <1 = <1,8 = <+1 +<m1, <2 = <2,8 = <+2, f(r)=2G±1}^1(r)l2j(r) <±j(r)=(1—^(ryij(r))<±j (j=i,2), 111 (r) = cos01 (r), l12(r) = sin-01 (r) , а плотность армирования w1 (r) задается формулой (1) при k = 1. Второй тип структуры армирования (Рис. 1в). При радиально-окружной укладке волокон кусочнолинейные кривые текучести КМ пластины при ПНС являются шестиугольниками ABCDEF (N = 6), координаты угловых точек которых, согласно [17], определяются так (см. Рис. 2в): A :<1 = J1,1 = <+ +^1,<2 = J2,1 = <+ + ^2; B : <1 = <1,2 = —<-1, <2 = <2,2 = <+ + <^2; C: <1 = <1,3 = -a- -<-1,<2 = <2,3 = f D: <1 = <1,4 = —<f1 -<m1, <2 = <2,4 = -<f2 -<m2 ; E : <1 = <1,5 = <+1,<2 = <2,5 = -<- -<-2; F : <1 = <1,6 = <+1 +<m1, <2 = <2,6 = -f Здесь <±j(r)= (1-Щ (r))<±j, <±j(r)= <±]^j(r) (j= 1,2), Ro < r< R1; (22) плотность армирования w1 (r) вычисляется по формуле (1) при 01 (r) = 0 (k = 1), а функция w2(r) может быть задана достаточно произвольно при выполнении неравенств (2); пределы текучести арматуры разных семейств могут различаться, то есть <± = <±]. Таким образом, равенства (19) и (21) при учете соотношений (1), (2), (20) и (22) в явном виде описывают напряжения <1,nи <2,n(1 < n < N) в неравенствах (16) для рассматриваемых типов структур армирования пластины, если кривая текучести материала связующей матрицы ее композиции соответствует модифицированному критерию Треска [27, 30] (подробное описание кривых на Рис. 2б и 2в приведено в разделе 5). Если повторить ход рассуждений из раздела 3 работы [17], вместо выражений (19) и (21) можно построить другие равенства для расчета угловых точек кривой текучести КМ-пластины при условии, что кусочно-линейная кривая текучести материала матрицы при ПНС не похожа на шестиугольник, изображенный на рисунке 2а, то есть соотносится с критерием текучести, отличным от модифицированного условия текучести Треска [27, 30], например, с критерием текучести Ишлинского–Ивлева [19]. 4. Верификация численного метода Для верификации представленного выше (см. раздел 2) численного подхода проведем сравнение с известными аналитическими решениями, полученными в [14, 22]. С этой целью полагаем: однородная пластина постоянной толщины 2h =1 см изготовлена из изотропного материала с одинаковыми пределами текучести при растяжении и сжатии: <m1 = <m2 = 151 МПа (это условно соответствует магниевому сплаву [1,31]); пластическое течение в материале ассоциируется с критерием текучести Треска; радиусы кромок пластины имеют значения: R0 = 0.25 м и R1 = 1 м; при r = R0 пластина жестко соединена с шайбой (см. (7) и (18)); внешняя кромка может быть шарнирно опертой или жестко защемленной. Эта составная конструкция нагружена только силой Pz, которая приложена к шайбе, поэтому в выражениях (4) принято Pz = 1 и pjz (r) = 0, а в соотношениях (9), (10) и (15)gz (r) = gr(r) = 0, G = 0, МП = МП = 0, Q1 = T1 = 0, Q1 = Tr1= 0 и mП = mП = 0. В случае шарнирного опирания на внешней кромке пластины (при неучете последнего равенства в (17) и задании Ui = vi =0) точное значение предельно допустимой силы Pz можно найти из решения нелинейной системы [22]: P(п -Ro) + <(r3-R3)/3+RoMo = 0, Pln(r2/r1)+ P (R1 -гз) +< (R3-r|)/3+Mor3-2R1Mo = 0, P = -Mor2/(r2-r2), q = Mo/(r2-r2), Pz = 2n(Mo-P), q = 2q, где M0 = h2ff—1; r1, r2 и r3 — радиусы окружностей, переход через которые сопровождается сменой режима пластического течения на кривой текучести Треска, причем R0 < r1 < r2 < r3 < R1 (не следует путать с узлами сетки rk, введенными в разделе 2 при дискретизации задачи). При задании же на внешней кромке жесткой заделки (см. (17) при u1 = v^ =0 и Р1 =0) точное значение нагрузки Pz определяется из системы нелинейных уравнений: P (n-Ro)+q(r3-R33)/3+MoRo = 0, P ln(r2/ri) + q(r2-r2)/2+Mo =0, P (r4 - ri) + q(r3 - r3)/3+Mori - 2М0Г4 = 0, (P-2M0)ln(R1/r4)+q(Rl-rl)/2-Mo = 0, P = -^°4, q= ^°2 , Pz = 2n(Mo-P), q = 2q, r -r r -r где использованы обозначения, аналогичные принятым в (23). В таблице приведены расчетные значения предельно допустимой силы Pz, полученные по формулам (23) и (24), а также численно (см. описание подхода см. в разделе 2) при разной степени дискретизации рассматриваемой задачи (при разном количестве K узлов сетки, вводимой на отрезке r G [R0,R1]). Из таблицы видно, что значения силы Pz , , находимые численно в пределе (с увеличением K) стремятся к аналитическим решениям, что демонстрирует сходимость численного решения. Значения нагрузки Pz, установленные численно при K = 101 (последний столбец), превышают точные значения (второй столбец) не более чем на 1.2%, поэтому далее численные расчеты в настоящем исследовании будем проводить при K = 101. Таблица. Значения предельно допустимой силы Pz, кН, приложенной к шайбе в однородной изотропной пластине, пластическое течение КМ которой соотносится с критерием текучести Треска Опора на внешней кромке R1 Аналитическое решение (23) и (24) Численное решение K=7 K=13 K=26 K=51 K=101 Шарнирное опирание 120.73 190.02 151.58 139.64 127.03 121.91 Жесткая заделка 139.78 248.29 194.86 168.22 149.91 141.53 5. Обсуждение результатов расчетов пластин из разносопротивляющихся материалов Прежде всего отметим, что случай поперечного нагружения пластины исключаем и рассматриваем только нагружение равномерно распределенной по всей составной конструкции поперечной силой pZ, то есть приложенной и к кольцевой пластине, и к шайбе. При этом в соотношениях (4) Pz = nR2p0, Pz (r)= pz0 =const. (25) После подстановки равенств (25) в (5) с учетом условий (7) и (8) и значений Q1 = T1 = 0, mП = тП = 0 приходим к тому, что сомножитель в левой части уравнения (5), заключенный в квадратные скобки, становится равным нулю. В предельном же состоянии конструкции правая часть в соотношении (5) отлична от нуля. Таким образом, силовой параметр |p| → ∞, а значит, при рассматриваемом виде нагружения эта составная конструкция обладает неограниченно большой несущей способностью. Однако, если при наличии равенств (25) выполняются, например, неравенства QZ = 0 и/или T1 = 0, и/или тП = 0, и/или тП = 0, то предельная нагрузка, имеющая в этом случае конечное значение p∗, все-таки может быть определена из экстремальной задачи, сформулированной в разделе 2. Далее, в данном разделе, для конкретности, полагаем: как и в работах [12, 14, 22, 23], составная конструкция нагружена только силой Pz (хотя это и не принципиально), которая приложена лишь к шайбе, то есть в равенстве (5) (и, как следствие, в соотношениях (9), (10) и (15)) считаем, что Pz = -1 Н, QZ = T1 = 0, mП = mП = 0, pz (r) = gz(r) = gr(r) = 0, G = 0, Q1 = T1 = 0 и M^ = МП = 0. У радиусов Ro, R1 и толщины пластины 2h те же значения, что и в разделе 4. С целью демонстрации неприменимости (с практической точки зрения) аналитических решений, полученных в [12, 14, 23] для пластин из разносопротивляющихся материалов в предположении, что в их предельном состоянии можно не учитывать возникающие мембранные усилия, рассмотрим сначала следующую модельную задачу. Пусть кольцевая пластина является однородной и изотропной, причем ее пределы текучести при растяжении и сжатии существенно различны: a—1 = a—2 = 0.29 МПа, am1 = am2 = 2.9 МПа (таким отношением o—i/ami = 1/10 (i = 1,2) обладают, например, бетоны [32]). Пластическое течение в КМ-пластины ассоциируется с критерием Ху [27]. Численный расчет, выполненный по формулам раздела 2, показал, что для пластины, жестко защемленной на внешней кромке и жестко скрепленной с шайбой, предельная нагрузка равняется |PZ | = 0.9926 кН. На рисунке 3 пунктирные кривые 1 и 1’ характеризуют для этой задачи, соответственно, зависимости v(r) и u(r), нормированные так, чтобы v0 = -1 м/с. Если в тестовых задачах (см. разд. 4) при чисто поперечном изгибе пластин скорость радиального перемещения u (r) в численном решении имеет порядок 10-7V0, то есть там зависимость u(r) можно было рассматривать как машинный нуль по сравнению со значением v0, то, согласно поведению кривой 1’ на рисунке 3, в пластине, изготовленной из материала, по-разному сопротивляющегося растяжению и сжатию, в предельном состоянии радиальная скорость u(r) достигает значений порядка 2% от величины v0 (см. кривую 1 при 0 < r < 0.25 м). Так как для жесткопластической пластины вклад в диссипативную функцию D (см. (11)–(13)) изгибающих моментов пропорционален h2, а вклад мембранных усилий есть h [11], то для относительно тонкой пластины (h/(R1 — R0) ^ 1/50) эти вклады будут уже сопоставимыми, и пренебрегать мембранными усилиями (как это сделано в [12, 14, 23]) уже нельзя. Об этом же свидетельствует и характер кривой 1 на рисунке 3 (зависимость v (r)), которая качественно отличается от аналогичных кривых, полученных в работах [12, 14, 23] без учета мембранных усилий в предельном состоянии составной конструкции. Действительно, зависимости v(r), определенные в [12,14, 23], качественно похожи на такую же зависимость, рассчитанную в основополагающей работе [22], но в ней, в отличие от [12, 14,23], рассмотрена пластина из материала, одинаково сопротивляющегося растяжению и сжатию. Во всех этих публикациях эпюры скоростей прогибов v (r) качественно аналогичны кривой 4 на рисунке 3 (подробнее эта кривая будет описана ниже). Как видно, внутри области изгибного деформирования (R0< r < R1) кривой 4 присущ горизонтальный участок (0.54 < r< 0.685 м), других горизонтальных участков на этой кривой при r>R0 = 0.25 м нет. Кривая же 1 на рисунке 3 не имеет внутреннего горизонтального участка, однако подобный участок наблюдается справа (0.94 < r< R1 = 1 м). Последнее обстоятельство означает, что в предельном состоянии изгибаемой пластины, изготовленной из разносопротивляющихся материалов, в окрестности ее внешней кромки может возникнуть абсолютно жесткая, не деформируемая подобласть. В работах же [12, 14, 23] возможность появления в окрестности внешней кромки радиуса R1 такой абсолютно жесткой подобласти теоретически не предсказана. Рис. 3. Зависимости от полярного радиуса скоростей прогиба v (г) и радиального смещения u (r) точек срединной плоскости пластины из материала различной композиции при подвижной заделке внутренней кромки и разных условиях опирания внешней кромки: жесткое защемление, материал бетон - v(r) (кривая 1) и u (r) (кривая 1’); жесткое защемление, армирование по логарифмическим спиралям с разными углами V1 = —V0 - v (r) при V1 = 0 (кривая 2), при V1 = 8п/21 (кривая 3), при V1 = п/2 (кривая 4); подвижное опирание, радиально-окружное армирование, определяемое формулами (29) и (30) при ш0= 0.7- v(r) (кривая 5) Проведенный автором численный анализ показывает, что полученные в [12, 14, 23] полные решения для изгибаемых однородных и композитных пластин из разносопротивляющихся материалов без учета возникающих в их предельном состоянии мембранных усилий являются чисто формальными, не имеющими в общем случае (при сильно различающихся пределах текучести на растяжение и сжатие) практического значения. Далее в настоящем исследовании оценим влияние параметров армирования (направлений и плотностей) на величину предельной нагрузки Pz , которую может выдержать КМ-пластина, покоящаяся на несжимаемом жидком основании. Жесткопластические материалы компонентов композиции обладают разными пределами текучести при растяжении и сжатии, а именно: пластина изготовлена из изотропного магниевого сплава МА2 (^m1 = ат2 = 151 МПа и am1 = am2 = 113 МПа [31]) и усилена двумя семействами стальной проволоки марки 35ХГСНА (ст+ = 1554 МПа и а— = 1754 МПа, k =1,2 [31]). [k] [k] 5.1. Влияние углов армирования при заданном общем объеме арматуры Рассмотрим частный случай спирального армирования, когда стальная проволока уложена по прямолинейным наклонным траекториям (Рис. 1б). Эта структура наиболее просто может быть реализована на практике. При этом углы армирования ^k (r) в силу осевой симметрии конструкции определяются по формуле Клеро [33]: rsin^k (r) = R0sin^° = const > 0 (k =1,2), R0 < r < R1, где ^k — значение угла ^k, задаваемое при r = R0 (см. Рис. 1 б, где ^° = п/4). При такой укладке силовых элементов, согласно выражениям (1), с учетом (26) получаем, что плотности армирования wk (r) монотонно убывают с увеличением r, но остаются положительными при wk > 0 (k =1,2). Если принять w0 = w0 и ^° = —^°, то из соотношений (1) и (26) вытекает: w1 (r) = w2 (r) и ^1 (r) = —ф2 (r). Так как функции wk (r) являются положительными и убывающими, выполнимость физического ограничения (2) достаточно проверять только на внутренней кромке пластины (при r = R0). Объем армированной пластины (Vp) и общий объем силовых элементов в ней (Vf ) имеют выражения: R1 R1 Vp = 2п J" 2h(r)rdr, Vf = V1 +V2, Vk = 2п 2h(r)wk (r)rdr (k =1,2). (27) R0 R0 Как и выше, рассмотрим КМ-пластины постоянной толщины 2h(r) = const, причем для структуры армирования, которая относится к первому типу, с параметрами (1) и (26) при углах ф0 = —ф0 = п/3 примем значения w0 = w0 = 0.35. При этом физическое ограничение (2) выполняется во всех точках конструкции с максимально допустимым значением суммарной плотности армирования wm = 0.7. Значение относительного объема волокон Ω ≡ Vf /Vd (см. (27) при учете (1) и (26)) в такой КМ-пластине возьмем за эталонное: Me = 0.1589. Отметим, что на рисунке 2б изображены графики текучести в безразмерных осредненных напряжениях di = <^/<7+1 (i = 1,2), рассчитанные в трех точках пластины с заданной структурой армирования (см. формулы (19) и (20)). При этом кривая 1 получена при r = R0 (ф1 (r) = ф0 = п/3), кривая 2 — при r = vT.5R0(в этой точке ^1(r) = п/4) и кривая 3 — при r = R1, где ф1 (r)« 0.218 рад. Все кривые являются восьмиугольниками, причем кривая 2 симметрична относительно прямой <2 = д-1, а кривая 3 визуально почти неотличима от шестиугольника. Графики на рисунке 2б демонстрирует существенную (как количественную, так и качественную) изменяемость по радиусу r текучести композиции пластины с обсуждаемой структурой армирования. Будем изменять углы ф0 = —ф0 в диапазоне ф0 G [0,п/3], а плотности армирования w0 = w0 при различных значениях ψ10выберем такими, чтобы относительный общий расход волокон Ω, рассчитанный по формулам (1), (26) и (27), был равен эталонному значению (28). На интервале ф0 G (п/3,п/2) при такой структуре армирования нарушается физическое ограничение (2), если накладывается требование M = Me, поэтому углы ф0 из этого интервала не рассматриваем. На рисунке 4 изображены зависимости |Pz (ф°) |. Штриховые кривые 1 -4 рассчитаны при укладке арматуры по прямолинейным наклонным траекториям (см. Рис. 1б). Кривая 1 получена для случая жесткого скрепления КМ-пластины с шайбой и при неподвижном защемлении ее внешней кромки (см. (7), (17) и (18) при u^ = vj =0 и ^ = 0); кривая 2 отвечает жесткому скреплению пластины с шайбой и неподвижному шарнирному опиранию ее внешней кромки (см. (7), (18) и два первых равенства (17) при u^ = v X = 0); кривая 3 соответствует шарнирному скреплению пластины с шайбой и жесткому защемлению ее внешней кромки (см. (7) и (17) при u^ = v X = 0 и ^ =0); кривая 4 соотносится с шарнирным скреплением пластины с шайбой и неподвижным шарнирным опиранием ее внешней кромки (см. (7) и два первых равенства (17) при u^ = v X = 0). Кривые 1 -4 монотонно убывают, а значит, из всех структур армирования по прямолинейным траекториям максимальную несущую способность КМ-пластинам обеспечивает структура с укладкой волокон в радиальном направлении (при ф 0 = —ф0 = 0). Как видно, обсуждаемые кривые имеют незначительную изменяемость (особенно кривая 4), следовательно, варьирование углов ф0 = —ф0, по крайней мере в диапазоне 0 < ф0 < 0.4 рад, слабо влияет на значение предельной нагрузки Pz при данном типе армирования пластины. Это обстоятельство может представлять особый интерес с точки зрения практической реализации таких структур, а именно: в рамках технологического процесса изготовления рациональных КМ-пластин (при ф0 = —ф0 = 0) не обязательно армирующую проволоку укладывать строго радиально. Рис. 4. Зависимость от угла армирования модуля предельной поперечной нагрузки, действующей на жесткую шайбу, на контакте с внутренней кромкой КМ-пластины при разных вариантах спиральной укладки волокон; армирование по прямолинейным траекториям (кривые 1–4); армирование по логарифмическим спиралям (кривые1’–4’); виды граничных условий на кромках пластины: 1, 1’ — подвижное опирание на внутренней кромке и жесткая заделка на внешней; 2, 2’ — подвижное опирание и неподвижный шарнир; 3, 3’ — подвижный шарнир и жесткая заделка; 4, 4’ — подвижный шарнир и неподвижный шарнир Рассмотрим другой вариант спирального армирования — укладку по логарифмическим спиралям: ^1 (r) = —^2 (r) = ^0, R0< r< R1 (см. Рис. 1 а). Для КМ-пластин постоянной толщины в этом случае из выражения (1) вытекает: wk(r) = RoW/r (k =1,2), Ro< r<R, (29) то есть функции wk (r) не зависят от углов армирования ^0и являются монотонно убывающими. Если при этом w0 = w0, то из (29) следует w1(r) = w2(r), а значит, при заданных плотностях армирования w0 = w0 и произвольных углах армирования ^0 G [0,п/2) общий расход волокон в пластинах с укладкой по логарифмическим спиралям фиксированный. На основании равенств (27) и (29) получаем, что при w0 = w0= 0.1986 относительный объем волокон в пластине с такой структурой армирования равен эталонному значению (28). Графики зависимостей предельной нагрузки |Pz| от углов армирования по логарифмическим спиралям ψ10 представлены на рисунке 4 сплошными линиями 1’–4’, при укладке по прямолинейным траекториям Кривые рассчитаны при одинаковых видах скрепления КМ-пластины с шайбой и способах опирания на внешней кромке пластины. Видно, что кривые 1’–4’ обладают значительной изменяемостью. Однако ипри таком типе армирования из всех сравниваемых структур максимально возможное значение предельной нагрузки |Pz | опять-таки е обеспечивает укладка волокон в радиальном направлении (см. ординаты точек на кривых 1’-4’ при ^° = 0), которое, как уже отмечалось, совпадает с одним из направлений главных напряжений в композиции изгибаемой кольцевой пластины. Вернемся к рисунку 3, на котором кривые 2-4 характеризуют зависимости v(r), рассчитанные при разных значениях углов армирования пластины ψ10по логарифмическим спиралям и при подвижном опирании ее обеих кромок в этих случаях зависимость | Pz (^0) | описывается кривой Г рисунка 4). Графикам на рисунке 3 отвечают: кривой 2 значение ^0 = 0 (структура с радиальным армированием), кривой 3 — у ^° = 8п/21 (спиральное армирование), кривой 4 — ^° = п/2 (окружная структура) при задании интенсивности армирования по формуле (29) для обоих семейств волокон. Заметим, что зависимости u (r) для этих типов армирования пластины на рисунке 3 не изображены, потому что они визуально практически лежат на оси абсцисс в силу малого различия пределов текучести компонентов металлокомпозиции при их растяжении и сжатии. Изломы на кривых 2–4 рисунка 3 свидетельствуют о том, что в предельном состоянии изгибаемой КМ-пластины появляются пластические шарниры. Это обстоятельство ранее было обнаружено аналитически для однородных (в том числе и композитных) пластин, покоящихся на несжимаемом жидком основании [12, 14, 22, 23]. Однако сравнение кривых 2–4 показывает, что в предельном состоянии армированной пластины графики скорости прогиба v(r) существенно зависят от ее структуры, причем эпюры v(r) при разных углах армирования ^° могут различаться не только количественно, но и качественно. Так, кривые 2 и 3 имеют на один шарнир меньше, чем кривая 4, то есть у пластины с окружной укладкой волокон в предельном состоянии на один пластический шарнир больше, чем у пластины с армированием по логарифмическим спиралям при ^°= п/2 (в частности, и при радиальном армировании). Выше отмечалось, что в работах [12, 14, 23], где в предельном состоянии конструкции не учитывались мембранные усилия, зависимости v (r) получаются качественно аналогичными кривой 4 рисунка 3, то есть возможность изменения количества пластических шарниров с изменением структуры армирования в [12, 14] теоретически не была обнаружена. 5.2. Влияние плотностей армирования при заданных направлениях укладки волокон В композиции осесимметрично изгибаемой кольцевой пластины влияние варьирования интенсивностей армирования wk (r) на величину предельной нагрузки Pz при заданных углах армирования ^к(к = 1,2) продемонстрируем на примере структуры с радиально-окружной укладкой волокон (см. Рис. 1в), у которой направления армирования совпадают с направлениями главных напряжений и ассоциированными с ними главными скоростями деформаций. Структуры армирования, обладающие таким свойством, традиционно принято считать рациональными [26]. Об этом, в частности, свидетельствуют и особенности поведения кривых на рисунке 4: из всех спиральных структур армирования, рассмотренных в подразделе 5.1, максимальные по модулю значения предельной нагрузки достигаются в вырожденном случае — при укладке волокон в радиальном направлении (^0 = 0). При радиально-окружном армировании первое (к = 1) семейство силовых элементов укладывается вдоль полярного радиуса (^1 = 0), поэтому в силу 2h(r) = const плотность армирования w1(r), согласно (1), выражается как (29). Второе (к = 2) семейство арматуры укладывается по окружным траекториям (^2 = п/2), поэтому интенсивность армирования w2(r) при выполнении физических ограничений (2) может задаваться достаточно произвольно. Например, можно принять: U2(r)= w0 — wi(r), Ro < r< R1, (30) где функция w1 (r) определяется соотношением (29). Из (30) вытекает: для данной структуры суммарная интенсивность армирования (см. (2)) постоянна по радиусу (wP (r) = w0 = const); относительное же объемное содержание волокон ^ = Vf /Vd = w0 (см. (27) при учете (29) и (30)). На рисунке 2в представлены кривые текучести такой металлокомпозиции (см. (29) и (30)) в безразмерных главных усредненных напряжениях Oi = oi/a^^ (i = 1, 2), полученные при значении "o= 0.7 в трех точках КМ-пластины (см. соотношения (21) при учете (22)): при r = R0 (на внутренней кромке) — кривая 1; при r = (Ro+Ri)/3 (во внутренней точке) — кривая 2; при r = R1 (на внешней кромке) — кривая 3. Сравнение этих кривых позволяет проследить за тем, как существенно изменяются кривые текучести рассматриваемой композиции вдоль полярного радиуса r, хотя при радиально-окружной укладке волокон суммарная плотность армирования в КМ-пластине является величиной постоянной. Следовательно, проведенные в [14] расчеты, выполненные в предположении об однородности радиально-окружной структуры армирования (то есть при условии, что кривая текучести композиции во всех точках пластины фиксированная), являются идеализированными, даже несмотря на то, что в [14] возникновение мембранных усилий в предельном состоянии изгибаемой КМ-пластины во внимание не принималось. Выше отмечалось, что при определении интенсивности армирования окружного семейства волокон формулой (30) выполняется равенство: П = "o, а значит, при такой укладке волокон невозможно варьировать функции "i(r) и "2(r) так, чтобы при этом обеспечивалось условие П = Пе (см. (28)). Откажемся временно от выражения (30) и для конкретности представим интенсивность армирования второго семейства волокон линейной функцией: "2(r) = r-R0 R1-R0 "2+ R1 -r R1-R0 ω20, R0⩽r⩽R1, где w° = w2(Ro) и "2 = w2(R1). С целью обоснованного сопоставления предельных нагрузок Pz, получаемых для составных конструкций с радиально-окружной и спиральной укладкой волокон, потребуем, чтобы в них при армировании по радиальным и окружным траекториям относительный объем волокон Ω равнялся прежнему эталонному значению (28). Так как рассматриваются пластины постоянной толщины, исходя из равенств (27) при учете выражений (29)(к = 1) и (31) будем иметь: Из соотношения (33) следует: ω 1 2= Vp = 2nh(R2-R2), Vi = 4nhRo(Ri-Ro^l, 4nh R1- R0 R31 -R30 -R0 R21 10 ω2- ω2 R02 (R3 - R0)+ 2 “iRl (Ri -R(,) V2(Ri-Ro) ,( Ri-R RR2!-R2 \ n 4nh 3--R1 2^ J"2 где V2 нужно выразить через Пе. Используя второе равенство (27), (32) и П = Vf /Vd = Пе, получаем искомую зависимость: V2 = V2 Н) = 2nh[Пе(Ri-R2) -2Ro(Ri -Ro>l]. Учитывая соотношения (35) и заданное значение Ωe (см. (28)), параметры ω10и ω20в выражении (34) можно варьировать, то есть на основании равенств (29) и (31) управлять распределением плотностей армирования "i(r) и "2(r). При этом необходимо контролировать выполнение физического ограничения (2) при "o> 0, "o> 0 и "2 > 0. В работе [17] для аналогичных составных КМ-конструкций, но не покоящихся на несжимаемом жидком основании, были проведены расчеты при разных значениях ω10и ω20в (34). Показано, что при фиксированном значении ω10максимальную несущую способность имеют КМ-пластины со структурой, в которой значение ω20 таково, что выполняется требование "2 =0. Предварительно осуществленные расчеты показали, что этот результат справедлив и в рамках настоящего исследования. Поэтому далее полагаем "2 = 0, и из (34) при учете (35) получаем: "0 = ( R - R - Ri R 2R\ i (Ri ^ [2Ro"0 - Пе (Ri + Ro)]. (36) Тогда из соотношений (29), (31) и (36) следует, что в этом случае плотности армирования "i(r) и "2(r) являются монотонно убывающими функциями, поэтому физическое ограничение (2) вполне достаточно проверять только на внутренней кромке (r = Ro) и следить за выполнением неравенств "o> 0 и "o> 0. На рисунке 5 приведены зависимости |Pz ("o) |, полученные для пластин с радиально-окружной укладкой волокон. Сплошные кривые 1 -5 рассчитаны при использовании соотношений (29), (31), (36) и "2 = 0, причем кривые 1–4, как и штриховые кривые 1’–4’, определены при тех же вариантах опирания КМ-пластин и их скрепления с шайбой, что и кривые 1–4, 1’–4’ на рисунке 4 соответственно. Кривые 1–4 на рисунке 5 являются монотонно возрастающими, ординаты их точек достигают максимальных значений при ш0 = 0.3972, как и при радиальной структуре армирования: ш2 (r) = 0. Напомним, что при ш0 > 0.3972 нарушается физическое ограничение (2) для рассматриваемых структур армирования, поэтому при ш0 > 0.3972 кривые 1 -4 на рисунке 5 не изображены. Из рисунка видно, что с увеличением номера изменяемость кривых значительно уменьшается и, например, для кривой 4 становится почти несущественной (ординаты ее левой и правой точек различаются всего на 10.8%). Сопоставление максимальных значений ординат точек кривых 1–4 на рисунках 4 и 5 показывает, что они полностью совпадают, так как относятся к одной и той же укладке волокон в радиальном направлении, которая может считаться оптимальной на множестве обсуждаемых здесь структур армирования. Выше анализировались зависимости предельной нагрузки |Pz | от параметров армирования ψ 0и ω 0для составных конструкций с фиксированным относительным объемом силовых элементов в них (см. (28)). Теперь рассмотрим структуры армирования, на которые это требование не накладывается. КМ-пластины по-прежнему имеют радиально-окружную структуру, причем плотность армирования радиальным семейством волокон ш 1 (r) вычисляется по формуле (29) при k = 1, а интенсивность армирования окружным семейством волокон ш2(r) задается соотношением (30). Как уже отмечалось, при такой структуре суммарная интенсивность армирования ωΣ (см. (2)) постоянна по радиусу r и поэтому равна Ω, а параметр ω10может принимать значения из интервала ш0G [0,0.7]. Штриховые кривые 1’-5’ на рисунке 5 характеризуют такие зависимости: |Pz (ш0) | = |Pz (^)| (описание кривых 5 и 5’ приводится ниже). При ш0 = 0 ординаты точек указанных кривых определяют значения |Pz | для однородных изотропных кольцевых пластин из магниевого сплава МА2. Кривые 1’–4’ на рисунке 5 возрастают почти по линейному закону, и их изменяемость гораздо заметнее изменяемости кривых 1–4. Монотонное возрастание кривых 1’–4’ демонстрирует эффект увеличения несущей способности кольцевых пластин, покоящихся на несжимаемом жидком основании, за счет их армирования. Сопоставление ординат левых и правых точек на данных кривых свидетельствует, что армирование рассматриваемых составных конструкций позволяет увеличить их несущую способность в 5.4–5.9 раз (в зависимости от способа закрепления кромок кольцевой КМ-пластины). При значении ш0= ^e (см. равенство (28)) ординаты точек на кривых 1’-4’ рисунка 5 примерно на 25–30% меньше ординат правых точек на кривых 1–4 . Следовательно, при фиксированном расходе арматуры (^ = ^e) укладка волокон по радиальным и окружным траекториям с плотностями армирования (29) и (30) дает значительно меньший эффект, чем аналогичная структура армирования с параметрами (29), (31), (36) и ш1 = 0 при задании ш0= 0.3972. Сравнение же ординат правых точек на кривых 1’-4’ и 1 -4, соответственно, показывает, что использование радиально-окружной структуры с последним вариантом распределения интенсивностей армирования (см. кривые 1–4) приводит к значениям |Pz | примерно на 50% меньшим, чем при плотностях армирования, находимым по формулам (29) и (30) при ш0= 0.7 (см. кривые 1’-4’). Однако относительный объем волокон при этом варианте распределения интенсивностей армирования на 76% больше, чем в случае параметров армирования, описываемых соотношениями (29), (31), (36) и ш2 =0 при ш0= 0.3972. Рис. 5. Зависимость на внутренней кромке КМ-пластины модуля предельной поперечной нагрузки, действующей на шайбу, от значения интенсивности армирования первым семейством волокон при разных типах радиально-окружных структур: армирование окружным семейством волокон с плотностью (31) (кривые 1–5) и с плотностью (30) (кривые 1’–5’); — те же способы закрепления кромок пластины, что и на рисунке 4 (кривые 1–4 и 1’–4’); подвижное опирание на обеих кромках (кривые 5 и 5’) Ранее обсуждались результаты расчетов (см. кривые 1–4 и 1’–4’, Рис. 4 и 5), выполненных при традиционных видах граничных условий на кромках КМ-пластины [12, 14, 22, 23]: подвижные в вертикальном направлении шарнир или заделка на внутренней кромке радиуса R0 ; неподвижные шарнир или заделка на внешней кромке радиуса R1. Сопоставление значений ординат точек на кривых 1–4 и 1’–4’ на рисунке 4 (или 5) при заданных величинах ψ10 или ω10 позволяет оценить влияние граничных условий на несущую способность армированных пластин. Однако разработанный и описанный в разделе 2 численный подход дает возможность получать решения рассматриваемых задач и при других (нетрадиционных) вариантах как закрепления, так и нагружения кромок КМ-пластины. В частности, на внешней кромке радиуса R1 может быть подвижное в вертикальном направлении опирание. При этом предполагается, что в предельном состоянии жидкость, с которой контактирует составная конструкция, не может перетекать с одной лицевой плоскости на другую. Так, на рисунке 3 кривая 5 определяет скорость прогиба v(r) в предельном состоянии КМ-пластины с подвижными опираниями на обеих ее кромках (r = R0 ,R1). При этом волокна уложены по радиальным и окружным траекториям с распределением интенсивностей армирования по формулам (29) (при k = 1) и (30) при задании w0 = we = 0.7. Правый горизонтальный участок на кривой 5 свидетельствует о том, что в предельном состоянии такой КМ-конструкции в окрестности ее внешней кромки (0.82 < r < 1.0 м) возникает абсолютно жесткая, не деформируемая подобласть. Подчеркнем еще раз, что возможность возникновения жестких подобластей в окрестности кромок кольцевых пластин, покоящихся на несжимаемом жидком основании, в работах [12, 14, 22, 23] ранее не была обнаружена. Поведение кривой 5 на интервале 0.25 < r< 0.82 м показывает: при рассматриваемом варианте граничных условий КМ-пластина в предельном состоянии изгибается так, что приобретает форму усеченного конуса. Подобный тип деформирования характерен для кольцевых пластин с жесткими вставками (шайбами), неподвижно закрепленных на внешней кромке и не покоящихся на несжимаемом жидком основании [17]. На рисунке 5 кривые 5 и 5’ характеризуют зависимости | Pz (ш°) | для пластин с обсуждаемым нетрадиционным вариантом граничных условий и радиально-окружной укладкой волокон с плотностями армирования, распределенными согласно формулам (29), (30) (кривая 5’) и (29), (31), (36) при учете (28) и w1 =0 (кривая 5). Как и кривые 1’–4’, кривая 5’ рисунка 5 монотонно возрастает по закону, близкому к линейному, тто есть и в этом случае (см. (29), (30)) наблюдается эффект увеличения несущей способности пластины с ростом общего расхода арматуры в ней. Кривая же 5, как и кривая 4, является почти горизонтальной (максимальное и минимальное значения ординат ее точек различаются всего на 10.7%). Это означает, что при некоторых вариантах граничных условий и некоторых типах армирования (см. (29), (31), (36) при учете (28) и w1 = 0) несущая способность КМ-конструкции может незначительно зависеть от распределения параметров армирования (в данной работе — от распределения плотностей армирования). С практической точки зрения в подобных ситуациях следует ориентироваться на структуру, которая наиболее просто реализуется технологически. Кривые 5 и 5’ на рисунке 5 располагаются существенно ниже кривых 1–4 и 1’–4’ соответственно (особенно по сравнению с кривыми 1 и 1’, которые, как и кривые 5 и 5’, рассчитаны при жестком защемлении обеих кромок пластины, но внешняя опора в первом случае предполагалась неподвижной). Следовательно, замена внешней неподвижной кромки составной КМ-конструкции, покоящейся на несжимаемом жидком основании, на подвижную кромку с сохранением остальных граничных условий прежними приводит к существенному (даже в разы) уменьшению ее несущей способности. 6. Заключение Рассмотрена задача вычисления верхней (кинематической) границы несущей способности армированной изгибаемой кольцевой пластины (возможно переменной толщины), покоящейся на жидком основании, которое предполагается несжимаемым. Имеющееся в пластине внутреннее отверстие закрыто абсолютно жесткой вставкой (шайбой). Пластина усилена двумя семействами непрерывных волокон постоянного поперечного сечения, уложены или по радиально-симметричным спиральным траекториям (у волокон один и тот же материал), или в радиальном и/или окружном направлениях (возможно, что материалы волокон разные). Такие структуры армирования обладают существенной неоднородностью. Жесткопластическим материалам компонентов композиций присущи разные пределы текучести при растяжении и сжатии; кроме того, материал связующей матрицы может обладать цилиндрической ортотропией (его пределы текучести в радиальном и окружном направлениях могут различаться). Использована двуслойная модель изгибного поведения кирхгофовской КМ-пластины, в каждом из фиктивных слоев которой напряженное состояние приближенно предполагается плоским и однородным в поперечном направлении. Пластическое течение в субструктурных элементах композиции ассоциировано с кусочно-линейными условиями текучести при ПНС (типа критериев Треска, Ху, Ишлинского–Ивлева [11, 19, 27]). Механическое поведение композиций описывается соотношениями структурной модели, учитывающей ПНС во всех их компонентах. Приведены расчетные формулы кривых текучести рассматриваемых композиций, волокна в которых изотропны и по-разному сопротивляются растяжению и сжатию, а пластическое течение в связующем подчиняется модифицированному критерию Ху [27, 30]. Для определения предельно допустимой нагрузки сформулирована задача на условный экстремум, базирующаяся на принципе виртуальной мощности. Проведена дискретизация задачи, ее численное решение строится с применением симплекс-метода теории линейного программирования [25]. Выполнена верификация разработанного численного алгоритма решения. Для этого решение на его основе сравнивается с известными аналитическими решениями, полученными для однородных изотропных пластин постоянной толщины, пластическое течение в которых подчиняется критерию Треска [22]. Продемонстрирована сходимость численного метода и хорошее согласование точных и численных результатов. На решении модельной задачи показано, что для однородных пластин из изотропных материалов, пределы текучести которых при растяжении и сжатии существенно различаются (например в 10 раз), в предельном состоянии эпюры скоростей прогибов имеют вид, качественно отличный от установленных ранее теоретически в [12, 14, 23], где возникновение мембранных усилий в изгибаемых конструкциях из разносопротивляющихся материалов не учитывалось. Последнее, как выяснено в настоящей работе, не корректно. Исследовано влияние варьирования параметров армирования (направлений и плотностей) на предельное значение поперечной нагрузки, приложенной к жесткой шайбе. Анализировались следующие структуры армирования: укладка волокон по прямолинейным радиально-симметричным траекториям (по геодезическим линиям), по логарифмическим спиралям, по радиальным и окружным траекториям. Показано, что в силу неоднородности таких структур кривые текучести соответствующих композиций существенно изменяются (не только количественно, но и качественно) вдоль полярного радиуса. Продемонстрировано, что при фиксированном расходе силовых элементов из всех обсуждаемых спиральных структур армирования (в том числе и по прямолинейным радиально-симметричным траекториям) наибольшую несущую способность составной изгибаемой конструкции обеспечивает армирование в радиальном направлении. Почти такие же (с точностью порядка 0.5%) значения предельно допустимой нагрузки при том же объеме волокон обеспечивает и структура с радиально-окружной укладкой силовых элементов и с рациональным (из заданного множества) распределением интенсивностей армирования. Рассмотрены различные граничные условия на кромках КМ-пластины: подвижные опирание или шарнир на внутренней кромке и неподвижная заделка или шарнир на внешней кромке. Показано, что наибольшее значение предельной нагрузки реализуется при жестком скреплении КМ-пластины с шайбой и жесткой заделке ее внешней кромки. Максимальной же несущей способностью обладают составные конструкции именно с такими типами граничных условий и с радиально-окружной структурой, при которой суммарная плотность армирования пластины постоянна вдоль полярного радиуса и равна максимально допустимому значению. Осуществлен расчет с нетрадиционными граничными условиями на кромках пластины, а именно жесткое скрепление с шайбой и подвижная в вертикальном направлении заделка внешней кромки. Продемонстрировано, что для КМ-пластин, покоящихся на несжимаемом жидком основании, при замене на их внешней кромке неподвижной заделки на подвижную предельная нагрузка уменьшается более чем вдвое. Работа выполнена в рамках государственного задания (№ госрегистрации 124021400036-7).