Численное решение краевых задач для уравнения Пуассона методом точечных источников поля

с условиями на границе dQ, соответствующими задаче Дирихле:

U=g.                                    (2)

Пусть для уравнения (1) известно частное решение U_o (г) (не обязательно с однородными условиями на границе):

^UQ^ = f(ry

Введём функцию u (г) = U (г) - U_o (г). Эта функция удовлетворяет однородному уравнению

Лапласа Ди = 0 с граничными условиями

Работа выполнена по грантам РФФИ № 13-07-00952-а и № 14-07-00705-а.

Для нахождения неизвестной функции и (г) можно теперь использовать МТИ, как это описано в [3-4]. В результате искомое решение краевой задачи найдём в виде суммы U (г) = и (г) + U_Q (г). Таким образом, для успешного решения краевой задачи для уравнения Пуассона необходимо сначала найти его частное решение. При этом могут использоваться различные подходы.

Как известно, правая часть f (г) в уравнении Пуассона LU =f (г) пропорциональна плотности заряда р(г) в точке с координатой г: f (г) = А'р(г). Коэффициент пропорциональности зависит от используемой системы единиц и, следовательно, от конкретного представления фундаментального решения для однородного уравнения (в данном случае уравнения Лапласа). Если фундаментальное решение, то есть потенциал поля, созданного в точке с координатой г единичным положительным зарядом, находящимся в точке с координатой R, имеет вид Im——т, то

f(r) = 2np(r). Для численного решения уравнения Пуассона область решения Q разбивается на небольшие элементарные участки боо/, каждый из которых имеет площадь 6s/. На этой площади находится заряд, приблизительно равный бу ~ ——6Si, 2п где г,. — координата центральной точки элементарного участка боо/.

В результате частное решение уравнения Пуассона можно приближённо представить в виде суммы:

1                     ( i )

Ц)(г)^УГ(г;)б5;1п — ,

/=1               V г - Г/ )

где N_P — число элементарных участков, на которые разбита область решения Q.

Таким образом, решаемая задача приводится к задаче численного решения уравнения Лапласа с помощью МТИ.

Рассмотрим конкретный, тестовый пример решения краевой задачи для уравнения Пуассона. Пусть правая часть в уравнении Пуассона f (r) = 2(№ +y2)cos(xy)-(x3y-xy3)sin(xy).(4)

Область решения представляет собой квадрат, сторона которого равна единице:

Q = {-0,5 <х < 0,5, -0,5<у <0,5}.(5)

Решается задача Дирихле с граничными условиями, соответствующими точному решению задачи

(/(r) = xysin(xy).(6)

Условия (4) — (6) соответствуют условиям задачи, решаемой в [10] путём разложения по собственным функциям уравнения Гельмгольца. При численном решении уравнения Пуассона с условиями (4) — (6) с помощью МТИ заряды, моделирующие искомое поле для уравнения Лапласа располагались на окружности радиусом, равном 1,25. Заряды бу, внутри области Q располагались в узлах равномерной прямоугольной сетки, покрывающей область Q. В узлах этой сетки на границе области Q располагались узлы коллокации, число которых соответствовало числу зарядов для уравнения Лапласа.

На рис. представлен график зависимости погрешности численного решения тестовой задачи от полного числа зарядов, моделирующих искомое поле (тонкая сплошная линия 2).

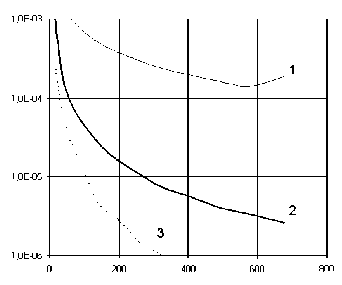
Рис. Зависимость погрешности численного решения от количества зарядов и узлов в прямоугольной (линии 1; 2) и круговой (линия 3) области, полученные различными способами: моделированием частного решения зарядами внутри области Q (линия 1) и использованием разложения правой части уравнения Пуассона в двумерный тригонометрический ряд (линии 2; 3)

Анализ данных, представленных на рис., показывает, что величина погрешности МТИ обратно пропорциональна числу зарядов (точнее, £ ~ /V"1-2). Это свидетельствует о достаточно медленном убывании погрешности МТИ с ростом числа зарядов. В то же время очевидно, что уже при небольшом числе зарядов, равном 25, погрешность £ ~ 1СГ3. Следовательно, в тех случаях, когда требования к точности решения не являются слишком строгими, применение МТИ для получения приближённого решения уравнения Пуассона описанным выше способом является вполне допустимым и разумным.

Повысить точность численного решения краевой задачи для уравнения Пуассона можно, аппроксимируя правую часть уравнения (1) тригонометрическим многочленом.

Известно [И], что функцию ф(х), определённую в узлах хо = xi, 26,..., хл на отрезке /можно аппроксимировать тригонометрическим многочленом, имеющим вид

ф(х)«^Ф^(х), где ф, =ф(х,), ^(х)= П k=X,k*i

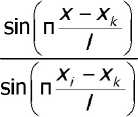
При использовании равноотстоящих узлов функции /^ (х) могут быть преобразованы в три гонометрические многочлены [12]. В результате получаем

1 П (         . п фМ^-Е (-1) 4>,Ssin(V+Q) п /=1 к           /(=1

где . 2пГ. пЛ , ,            fl Г2(/ —1) 2x_nV, 1^ . ,

' ^си< Д— п---Г " 2)у

Аналогичным образом функцию двух переменных f (х,у) (правая часть уравнения (1)), заданную в прямоугольнике со сторонами к, к и определённую в узлах прямоугольной равномерной сетки (х,,у₇), 1 < / <  n_x , 1 <  j <п_у, можно представить в виде тригонометрического многочлена

Г(х,у)

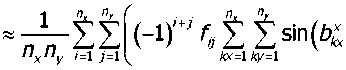
Y -L г^х

А ' L / кх

) sin (^у+с^)

где f_g = f ^х_иУдУ а параметры Ь^ .Ь^ .с^ .с^ и другие определяются по формулам, аналогич ным (7).

Так как частным решением уравнения Пуассона при f (x,y) = sin(bxx H-c^sin^y + ск)

является функция и₀ (г)

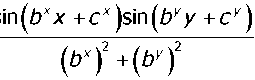
, то, учитывая линейность уравнения, част

ное решение уравнения (1) запишется в виде

U

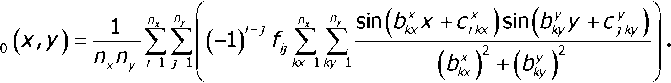
На рис. представлен график зависимости погрешности численного решения тестовой задачи от полного числа зарядов, моделирующих искомое поле (жирная сплошная линия 2), полученный с использованием частного решения (8). Видно, что погрешность решения в этом случае почти на два порядка ниже, чем в том случае, когда поле, соответствующее частному решению, моделируется зарядами, расположенными внутри области Q.

При решении краевой задачи для области Q, форма которой отличается от прямоугольной, строится прямоугольник минимальных размеров (для минимизации численной погрешности), охватывающий область Q; функция f (х,у) экстраполируется за пределы области Q вплоть до границ построенного прямоугольника. Далее находится численное решение краевой задачи описанным выше способом. При этом может оказаться, особенно при решении задач Дирихле, что погрешность численного решения для области Q окажется ниже, чем для прямоугольной области. Это объясняется тем, что в области Q отсутствуют участки прямоугольника, примыкающие к его вершинам, в которых погрешность аппроксимации функции f(x,y) наибольшая. Эту особенность описываемого здесь метода иллюстрирует пунктирная линия 5 на рис., построенная при решении тестовой задачи для круговой области радиусом R = 0,5. Очевидно, что точность решения для круговой области почти на порядок выше, чем для прямоугольной области. При использовании зарядов, расположенных внутри области решения непрямоугольной формы (линия 1 на рис.), точность решения значительно ухудшается.

Заключение. Полученные результаты свидетельствуют о возможности эффективного использования МТИ не только при решении краевых задач для уравнения Лапласа, но и для неоднородных уравнений эллиптического типа, например для уравнения Пуассона.

Следует отметить, что предложенный алгоритм получения частного решения уравнения Пуассона может применяться и к другим неоднородным уравнениям эллиптического типа, например к уравнению Гельмгольца. Возможно также обобщение предложенного метода решения уравнения Пуассона для трёхмерного случая.