Численное решение линеаризованной квазистационарной системы уравнений фазового поля с запаздыванием

В настоящей работе предложен численный метод решения линеаризованной квазистацио- нарной системы уравнений фазового поля [1] с запаздыванием v t (x, t) = Av(x, t) - Aw(x, t) + Фпv (x, •) + Ф12 w (x, •), (x, t) g [0, n] x[0, T],(1)

0 = v(x, t) + (в + A)w(x, t) + Ф21 vt (x, •) + Ф22 wt (x, •), (x, t) g [0, n] x[0, T],(2)

v(0, t) = v(n, t) = w(0, t) = w(n, t) = 0, t g[ 0, T],(3)

v (x, t) = ф( x, t), w (x, t) = H x, t), (x, t) G[0,n] x[-r ,0],(4)

где v t ( x , s ) = v ( x , t + s ), w t ( x , s ) = w ( x , t + s ) при s g [ - r ,0 ] , r >  0. При этом отображения Ф i 1 : v ( x , • ) ^ Z i i ( x , t ), Ф i 2 : w t ( x , • ) ^ z i ₂( x , t ) при каждом x G [ 0, n ] , t g [ 0, T ] линейно и непрерывно действуют из пространства C ( [ - r ,0 ] ; R ) в R .

Исследование разрешимости этой задачи в рамках начальной задачи u (t) = h (t), t g[- r ,0], (5) для операторно-дифференциального уравнения соболевского типа с запаздыванием

LU t (. t ) = Mu ( t ) + Ф u t + f ( t ), t g [ 0, T ] , (6) было проведено ранее в работах В.Е. Федорова и Е.А. Омельченко [2, 3]. Здесь U, F – банаховы пространства, u t ( s ) = u ( t + s ) при s g [ - r ,0 ] , операторы L : U ^ F , Ф : C ( [ - r ,0 ] ; U ) ^ F линейны и непрерывны, ker L ^ { 0 } , оператор M : dom M ^ F линеен, замкнут и плотно определен в U , f : [ 0, T ] ^ F . Особенность линейного эволюционного уравнения с запаздыванием (6) в том, что оно является вырожденным в смысле присутствия оператора при производной, не обратимого в силу наличия у него нетривиального ядра. Настоящая работа представляет собой шаг к завершению естественного цикла исследований задач вида (5), (6), заключающемуся в разработке численных методов решения класса задач.

^исленным аспектам исследования задач для уравнений с последействием, в том числе задач для функционально-дифференциально-алгебраических уравнений, которые относятся к классу уравнений вида (6), посвящены работы В.Г. Пименова и его учеников [4–6]. В этих работах, в частности, сконструировано семейство сеточных методов для численного решения эволюцион-

Математика

ных уравнений с, вообще говоря, нелинейной функцией запаздывания на основе идеи разделения конечномерной и бесконечномерной фазовых составляющих.

С помощью результатов работ [2, 3, 5, 6] авторами данной статьи исследована сходимость явной разностной схемы для задачи (1)-(4). В первом параграфе, следуя идее разделения конечномерной и бесконечномерной фазовых составляющих, показана сходимость сеточного метода для соответствующей задачи без запаздывания ( Ф ij = 0, i , j = 1,2). Во втором параграфе доказана сходимость разностной схемы, учитывающей запаздывание. При этом соответствующая схеме дискретная модель определяется стартовыми значениями, формулой продвижения на шаг и оператором интерполяции и поэтому относится к классу моделей, исследованному в [5, 6] в связи с рассмотрением невырожденных эволюционных уравнений. И, наконец, третий параграф посвящен конкретной программной реализации метода.

• 2.    Линеаризованная квазистационарная система уравнений фазового поля

Рассмотрим начально-краевую задачу для системы уравнений vt (x, t) = A v (x, t) -A w (x, t), (x, t) е[0,п] x[0, T ],(7)

0 = v (x, t) + (в + A) w (x, t), (x, t) е[0,п] x[0, T ],(8)

v(0, t) = v(п, t) = w(0, t) = w(п, t) = 0, t e [0, T],(9)

v (x ,0) = ^( x), x е [0,п],(10)

где в <  0, а v , w - искомые функции. Заметим, что начальное значение w ( x ,0 ) для одной из искомых функций w не задано. Однако, как показано в [7], задача (7)-(10) однозначно разрешима. В случае же задания обеих начальных функций v ( x ,0 ) , w ( x ,0 ) задача оказывается переопределенной и необходимо выполнение условий согласования данных задачи (7)-(10) для ее разрешимости.

Разобьем отрезок пространственной переменной [0,п] на части с шагом h = п/ N, определив тем самым точки x n = nh, n = 0, ^, N. Аналогичным образом разобьем временной отрезок [0, T] на части с шагом т > 0, получив точки разбиения tm = тт, m = 0,..., M. Приближенные значения функций v, w в узлах с координатами (xn, tm) будем обозначать через vm , wm. Рассмотрим сеточный метод

т

v m + 1 - 2 v m + v m 1 _ w m + 1 - 2 w m + w m - л h ²                    h ²

m = 0,..., M - 1,

где n = 1,

mmm

0 = v ^m + e w ^m + w ^{n + 1 2} w n ⁺ w ^{n - 1} , n n              h ²

N -1, с начальными условиями vn0 = ^( xn), n = 0,..., N,

m = 0,..., M ,

и граничными условиями vm=vNm=wm=wNm=0, m=0,...,m.

Невязкой метода (11), (12) назовем сеточную функцию Т m = ( T m П ) , где

m

T n

^{v (} x n , t m + 1 ) ^{- v (} x n , t m ) - ^{v (} x n + 1 , t m ) ^{- 2 v (} x n , t m ) ^{+ v (} x n - 1 , t m ) . т                                   h h-

+ w(xn+1, tm ) - 2 w(xn , tm ) + w(xn-1, tm ) h h- nn = v(xn, tm ) + ew(xn , tm ) +

^{w (} x n + 1 , t m ) ^{- 2 w (} x n , t m ) ^{+ w (} x n - 1 , t m ) h ²

через v(xn, tm), w(xn, tm) обозначены истинные значения решения v, w задачи (7)-(10) в соответ ствующих точках. Будем говорить, что невязка имеет порядок тp1 + hp2, если существует такая

Оме^ьченко Е.A., П^е^анова М.В., ^авыдов П.Н.

константа   C , не зависящая от τ и h , что

Ψ _n ^m ₂ ≤ C ( τ ^{p 1} + h ^{p 2} )для всех,

n = 1, ^ , N - 1, m = 0, ^ , M - 1.

Лемма 1. Пусть точное решение v , w задачи (7)–(10) таково, что функция v дважды непрерывно дифференцируема по t , функции v , w четырежды непрерывно дифференцируемы по x . Тогда невязка метода (11), (12) имеет порядок τ + h ².

Доказательство. С помощью тейлоровского разложения функций v ( x , t ) , w ( x , t ) получим выражения для невязки

ξm=- τv+  h2(v+w),ηm n 2tt 12 xxxx xxxx n

-

h ² w .□

12 ^xxxx

Исследуем устойчивость этой схемы методом разделения переменных.

Теорема 1. Пусть β < 0 . Тогда схема (11), (12) устойчива, если выполнено условие τ ≤ h ².

Доказательство. Обозначив через ρ _q ^m , σ _q ^m коэффициенты q -х гармоник на m -м слое, имеем

v ⁽ x n ,t m ) = p q e iq" , w ⁽ x n , t m ) = ^ q e qx , q = 0, ± 1, ± 2, -

Подстановка этих функций в (11), (12) приведет к равенствам

ρ _q ^{m + 1} - ρ _q ^m = τ ₂ (2 ρ _q ^m (cos qh - 1) - 2 σ _q ^m (cos qh - 1)), h

mm

0=ρqm+βσqm+

Из последнего равенства получим выражение

2 σ _q ^m

(cos qh - 1). h ²

и подставим его в (13), тогда

ρ _qm + 1 ₌ ρ _qm

^m σ _q

^m ρ _q

_{h 2} (1 - cos qh ) - β

2τ

1 - (1 - cos qh )1

L 2

h

Из того, что β< 0, следует неравенство rq ≡1-2τ2(1-cosqh)1 h              I

-

-

h ²

2(1 - cos qh ) - h ² β

h ²

2(1 - cos qh ) - h ² β

≤ 1

.

сразу для всех q ∈ N . Покажем, что r _q ≥- 1 при любом q ∈ N . Для этого надо показать, что

T

(1 - cos qh ) 1

h 2             I

Это неравенство выполняется при τ ≤ h ² .

В силу равенств (14) и (15)

-

h ²

2(1 - cos qh ) - h ² β

≤ 1.

m + 1 σ _q

m + 1 ρ _q

^m ρ _q

1 2t                I

1 - ^2 (1 - cos qh ) 1

h ²

-

2(1 - cos qh ) - h ² β

m = σ q^m

_{h 2}(1 - cos qh ) - β

_{h 2}(1 - cos qh ) - β

A

2 t_z

1 - h 2 (1 - cos qh ) ¹

-

_{h 2} (1 - cos qh ) - β

.

Математика

Поэтому коэффициент перехода для второй неизвестной функции также равен r q и поэтому рассматриваемая разностная схема является устойчивой при т <  h ² . □

Замечание 1. Анализ доказательства теоремы 1 приводит к выводу, что при в >  0 не представляется возможным доказать устойчивость предложенной разностной схемы и необходима ее модификация или выбор другого метода вычисления.

В качестве итога полученных результатов сформулируем теорему о сходимости, которая сразу следует из критерия Куранта [8], леммы 1 и теоремы 1.

Теорема 2. Пусть в <  0 и для разностной схемы (11), (12) т , h таковы, что т <  h ² . Тогда разностное решение сходится к точному решению задачи (7) - (10) с порядком не ниже т + h ².

• 3.    Система уравнений с запаздыванием

Вернемся к начально-краевой задаче с запаздыванием (1)-(4). Для отрезка пространственной переменной [0,п] имеем прежнее разбиение с шагом h = п / N и точками x n = nh, n = 0,., N . Временной отрезок теперь имеет вид [-r, T]. Для определенности считаем, что T / r - рациональное число, шаг разбиения т = T / M = r / L , где L, M е N, точки разбиения t m = mт, m = -L,...,0,...,M. Помимо приближений vn^, wm искомых функций v, w понадобится также дискретная предыстория в точке xn к моменту tk :

{ ( v m , w m ) } = { ( v m , w m ) : k - L <  m <  k } , n = 0, . , N , k = 0, . , M .

k

Предполагается также, что задан оператор интерполяции дискретной предыстории

N , Q [ — r ,0 ] — множество кусочно

I:{(vm,wm)} ^(gk,hk)e Q[—r,0]xQ[—r,0]. Здесь n = 0, k непрерывных функций на [-r,0] с конечным числом точек разрыва первого рода в точках разры ва непрерывных справа. Зададим норму: ||g||Q[-r Q1 = sup |g(s)| для gе Q[-r,0]. Будем считать, L , J sе[-r,0]

что линейные операторы Ф ij продолжимы на пространство Q [ - r ,0 ] ограниченным образом.

Следуя работам [4, 5], будем говорить, что оператор интерполяции имеет порядок погрешно сти тp на точном решении v, w, если существуют такие положительные константы С 1, С2,что для всех n = 0,.,N, к = 0,.,M и tе[tk -r,tk] выполняются неравенства

I g ^ ⁽ t ) ^{- v (} x n , t )| <  C 1, max ^{V m - v (} x n , t m )| ⁺ С 2 ^{т p} ,

I                      ।       k - L < m < kl।

I h n ⁽ t ) ^{- w (} x n , t )| <  ^C 1 , ^max w ^{m -} w ⁽ x n , t m )| ⁺ C 2 ^т p .

I                       ।        k - L < m < kl।

Рассмотрим разностную схему vm+1- vm nn

т

m mmm mm vn+1  2 vn + vn-1   wn+1  2 wn + wn-1        mm

, 2                  , 2        +ф11 gn +ф12 hn , hh о=vm + ewm+wmi-2wm+wmi.+ф 2, gnm+ф 22 hm,(17)

h где n = 1,.,N-1, m = 0,.,M -1 в (16) и m = 0,.,M в (17), с начальнымиусловиями vn = ^( Xn ,0), w0 = y( Xn ,0), n = 0,., N,(18)

g0( t) = ^( Xn, t), hn0( t) = ^( Xn, t), n = 0,., N, t е[-r ,0],(19)

и граничными условиями vm = vN = wm = wN = 0, m = 0,., M.(20)

Согласно результатам работ [2, 3] необходимым условием разрешимости задачи (1) - (4) является выполнение условия согласования начальных данных ф и у

0 = ф ( x ,0) + ( в + А ) у ( x ,0) + Ф ₂₁ ф ( x , • ) + Ф ₂₂ у ( x , • ), x е (0, п ).

Оме^ьченко Е.A., П^е^анова М.В.,       Чис^енное ^ешение ^инеа^изованной квазистациона^ной

^авыдов П.Н.                           системы у^авнений фазового по^^ с запаздыванием

По умолчанию считаем, что оно выполняется.

Невязкой метода (16), (17) назовем сеточную функцию / 7 ^ = ( 1 ^ , П ^ ), где

2 m = v ^{( x} n , t m + 1 ) ^- v ^{( x} n , t m ) - v ^{( x} n + 1 , t m ) ^{- 2} v ^{( x} n , t m ) ⁺ v ^{( x} n - 1 , t m ) . ⁿ               T                               h h

+ w(xn+1, tm ) 2w(xn , tm ) + w(xn-1, tm ) - Ф] 1Vtm (X„, •) - Ф; 2wtm (x , •), h 2

П n^m = v ( X n , t m ) + e w ( X n , t m ) + w ⁽ x ⁿ^ t m ) "  ² w ⁽ X" t m ) ⁺ w ⁽ x ⁿ — 1 , t m ) + Ф 21 Vm ( X n , " ) + Ф 22 w m ( X n ,").

h

Так же, как теорема 4 в [5], с помощью теоремы 1 настоящей работы об устойчивости схемы (11), (12), теорем 1 и 3 из [5] доказывается следующий результат.

Теорема 3. Пусть в < 0, т < h2, оператор I: R2L+2 ^ Q[-r,0] липшицев и имеет порядок погрешности тР0 на точном решении, невязка /7% имеет порядоктР1 + hp2. Тогда разностное решение сходится к точному решению задачи (1)-(4) с порядком тmin{p0’Р1} + hp2.

Отметим лишь, что требующаяся для доказательства теоремы липшицевость операторов Ф^ в данном случае очевидна, поскольку они линейны и ограничены.

• 4.    Численный эксперимент

Пусть Ф^д = aijg(-1) для gе Q[-1,0], i, j = 1, 2. Другими словами, система (1)-(4) имеет вид vt (x, t) = Av(x, t) - Aw(x, t) + аи v(x, t -1) + a12 w(x, t -1), (x, t) е [0,n] x [0, T],        (21)

0 = v ( x , t ) + ( в + A ) w ( x , t ) + a ₂₁ v ( x , t - 1) + a ₂₂ w ( x , t - 1), ( x , t ) е [0, n ] x [ 0, T ] ,        (22)

и снабжена краевыми и начальными условиями (3), (4). Разностная схема (16), (17) для нее при выборе, например, кусочно-постоянной или кусочно-линейной интерполяции будет иметь вид

V ^{m +1}- v m v _n v _n

т

m mmm vn+1 - 2 vn + vn-1   wn+1

h ²

^{- 2} w m ⁺ w m - 1       m - L      m - L

-----------^{+ a} 11 v n ^{+ a} 12 w n ,

h

mmm m m , wn+1 2 wn + wn-1       m - L       m - L

⁰ = v n ⁺ P w n ⁺---------------- ⁺ a 21 ^v n   ⁺ a 22 w n ,                  ⁽²⁴⁾

h где n = 1,^,N-1, m = 0,^,M -1 в (23) и m = 0,^,M в (24), с начальными условиями (18), (19) и граничными условиями (20). При этом порядок погрешности оператора кусочно-постоянной интерполяции на точном решении равен т, для кусочно-линейной интерполяции - т2 [9]. По аналогии с леммой 1, нетрудно доказать следующее утверждение.

Лемма 2. Пусть точное решение v , w задачи (21), (22), (3), (4) таково, что функция v дважды непрерывно дифференцируема по t , функции v , w четырежды непрерывно дифференцируемы по x . Тогда невязка метода (23), (24) имеет порядок т + h ².

Теорема 3 влечет

Следствие 1. Пусть в <  0, т <  h ², интерполяция кусочно-постоянна или кусочно-линейна. Тогда разностное решение сходится к точному решению задачи (1)-(4) с порядком т + h ².

На рис. 1 представлено решение (v,w) для параметров в = -0,75, T = 10, M = 1000, N = 16 c начальным условием v ( x ,0) = sin x , x е [0, п ] для задачи (7)-(10).

Математика

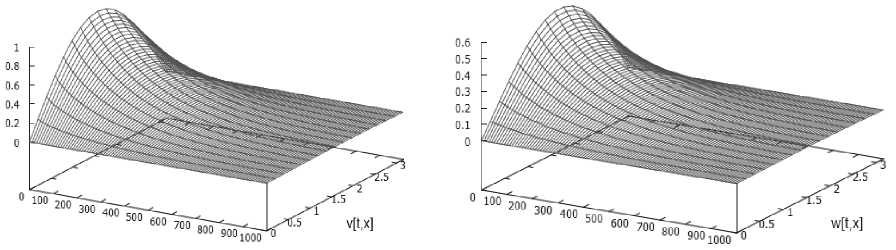
Рис. 1

Для задачи с запаздыванием (1)-(4) при значениях a 11 = 1, a ₁₂ = a ₂₁ = a 22 = 0 , в = -0,75, T = 10, M = 1000, N = 16, v ( x , t ) = ( t + 1)sin x , ( x , t ) e [0, ^ ] x [ - 1,0 ] решение ( v ,w ) показано на рис. 2.

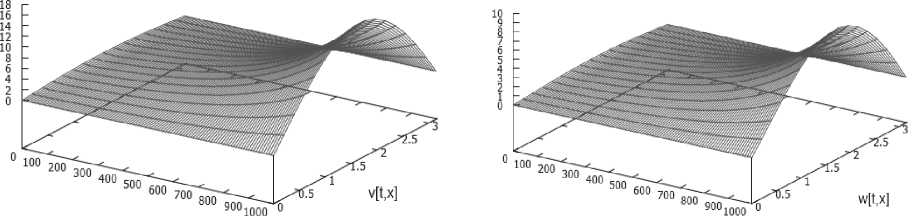
Рис. 2