Численное решение начально-конечной задачи для нестационарных систем леонтьевского типа

При построении математических моделей экономических систем и процессов широко используются балансовые модели [1,2]. Использование динамических моделей позволяет описать процесс изменения экономических показателей, установить непосредственную взаимосвязь между предыдущими и последующими этапами развития и тем самым приблизить анализ на основе экономико-математической модели к реальным условиям развития экономической системы. Кроме того отметим, что реальные модели обычно имеют большую размерность.

Рассмотрим в R n динамическую балансовую модель в виде нестационарной системы леонтьевского типа

Lx ( t ) = a (t ) Mx ( t ) + f ( t ),                                  (1)

где L, M - квадратные матрицы порядка n, причем det L = 0. Здесь a : [0; T] ^ R+ - скалярная функция, описывающая изменение во времени параметров взаимовлияния значений исследуемой системы, а матрица M - (L, p) -регулярна (т. е. существует ре С такая, что det(pL — M) ^ 0, и бесконечно удаленная точка является полюсом матриц-функции (pL — M)—1 порядка p ∈ N , здесь и далее N о = {0}u N). Вектор-функция f :[0; T] ^ Rn описывает внешние воздействия на систему. Отметим, что условие вырожденности системы det L = 0 является одной из отличительных черт систем леонтьевского типа, описывающих балансовые модели экономики, так как ресурсы определенного типа запасти нельзя [2]. Кроме того заметим, что балансовые модели зачастую имеют нестационарный вид, т. е. матрицы, входящие в систему (1), зависят от времени [3].

Системы леонтьевского типа являются конечномерным аналогом уравнений соболевского типа [4-6]. Данное исследование проведено в рамках теории вырожденных разрешающих семейств операторов [5]. Нестационарные уравнения соболевского типа впервые были рассмотрены в работе [7], далее для исследования таких уравнений было предложено использовать вырож- денные потоки операторов, которые являются аналогами разрешающих (полу)групп операторов [5] в стационарном случае. Разрешающие потоки матриц для нестационарных систем леонтьевского типа рассмотрены в работе [8].

При решении прикладных задач возникают ситуации, когда часть условий на искомую вектор-функцию нам известна в начальный момент времени, а остальные условия, в силу учета особенностей моделируемого процесса, нам известны в конечный момент времени. В таком случае адекватно рассматривать начально-конечные условия [9] для систем леонтьевского типа. Начально-конечную задачу будем рассматривать в следующем виде:

P_o( x (0) - x 0 ) = 0,     P t ( x ( T ) - X t ) = 0 ,                       (2)

где P , P - матрицы, с помощью которых задаются условия в начальный и конечный моменты времени, а векторы x ₀, x_T е R n описывают желаемые значения системы в начальный и конечный моменты времени соответственно. Начально-конечные условия могут быть применены при изучении различных математических моделей (см., например, [10-13]). Отметим, что начальноконечные условия являются обобщением [14] условий Шоуолтера-Сидорова [15], которые при исследовании вырожденных операторно-дифференциальных уравнений являются более естественными, так как снимают необходимость проверять согласование начальных данных [16].

Основной целью данной статьи является построение численного решения задачи (1), (2) без использования контурных интегралов, а также исследование сходимости этого решения. Численные решения начальных задач для систем леонтьевского типа исследуются, например, в работах [16-18].

Статья кроме введения, заключения и списка литературы содержит две части. В первой приводится необходимая информация для описания решений начальных задач для систем леонтьевского типа, для которых разрешающие семейства матриц описаны с помощью предельных переходов. Во второй части приводится основной результат статьи, а именно построено численное решение начально-конечной задачи (1), (2) и показана его сходимость к точному решению.

Решение начальных задач для нестационарной системы леонтьевского типа

Пусть L , M - квадратные матрицы порядка n , причем det L = 0 . Рассмотрим в R ⁿ нестационарную систему леонтьевского типа

LX( t ) = a ( t ) Mx (t ),

где a : [0; T ] ^ R₊ - скалярная функция, описывающая изменение во времени параметров взаимовлияния значений исследуемой системы, вектор-функция x : [0; T ] ^ R ⁿ искомая.

Будем называть матрицу M ( L , p ) -регулярной, если существует це С такая, что det( p L — M ) ^ 0 , и бесконечно удаленная точка является полюсом матриц-функции ( p L — M ) ^{— 1} порядка p е N_o . Этот термин является аналогом термина «регулярный пучок матриц p L — M » К. Вейерштрасса [19].

Лемма 1 [8]. Пусть матрица M ( L , p ) - регулярна ( p = 0, n — 1) . Тогда существуют проекторы, задаваемые с помощью матриц

P = lim ( ( L — k M ) ^{— 1} L ) p ^{+ 1}, Q = lim ( L ( L — k M ) ^{— 1} ) p ' . k ^^                         k ^^

Определение 1. Вектор-функция x е C 1([0;T];Rn) называется решением (3), если подстановка этой вектор-функции в уравнение (3) делает его верным тожеством. Решение x = x(t) уравнения (3) будем называть решением задачи Коши x (t 0) = x0

для уравнения (3) (коротко, задачи (3), (4)), если оно удовлетворяет условию Коши (4) при некотором х₀ е R ⁿ .

Определение 2. Вектор-функция x е C 1 ([0, T ]; R ⁿ ) называется решением (1), если подстановка этой вектор-функции в уравнение (1) делает его верным тожеством при некоторой вектор-

Математика

функции f :[0, T ] ^ R ⁿ . Решение x = x ( t ) уравнения (1) будем называть решением задачи Шоуолтера–Сидорова

P ( x ( t 0 ) - x 0 ) = 0                                      (5)

для уравнения (1) (коротко, задачи (1), (5)), если оно удовлетворяет условию (5) при некотором x ₀ е R ⁿ .

Используя аппроксимации Хилле-Уиддера-Поста [20] для матриц разрешающего потока [8], получим справедливость следующего утверждения.

Теорема 1 [8]. Пусть матрица M обратима и (L,p)-регулярна (p = 0,n — 1), а функция a е Cp+1([0,T];R+ ). Тогда для любой вектор-функции f : [0; T] ^ Rn, такой что Qf е C([0;T];Rn) и (En — Q)f е Cp+1([0; T];Rn), а также для любого начального значения x0 е Rn существует единственное решение x е C 1([0, T];Rn) задачи Шоуолтера-Сидорова

(1), (5), которое имеет вид x (t) = lim xk (t) = lim k ^^       k ^^

L

—

-

p

t

f

(

t

t                  1          t

⁺ I ^L / ^M I a ⁽ r ) ^dr

0 tk     k    s

k

X —1

A

k

L

kk

L — ¹ M

k

Z M ^— E ,

-

L — ¹ M

— 1

A p +1 V

A

q

q = 0

k

k

k

k

L

L

M

— 1

E n

-

k

t

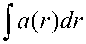
L

— 1

f

k

A — ¹

L — ¹ M

k

k

A

k

— 1

^x 0

\

+

p

L  f ( s ) ds

—

L — ¹ M

— 1

A p + 1V

k

L

k

1 d

k

q

f ( t )

Если дополнительно выполнено условие согласования

-

p

E n

—

L — ¹ M

— 1

A p +1 V

k

k

k

L

^x 0

a ( t ) dt

a ( t )

. (6)

Z m -' e ,

-

L — ¹ M

— 1

A p +1 V

A

q

(

q = 0

k

k

k

k

L

L

M

— 1

E n

-

L — ¹ M

— 1

A p +1 V

k

k

k

L

1 d

A

q

f ( t )

k a ( t ) dt

a ( t )

,

t = 0

то функция (6) является единственным решением задачи Коши (4) для уравнения (1).

Здесь и далее через Еп обозначена единичная матрица размера n . Отметим, что условие об ратимости матрицы M в теореме 1 не является ограничительным, так как при проведении замены в системе (1) всегда можно добиться его выполнения (подробнее см. в [8]).

2. Численное решение начально-конечной задачи для нестационарной системы леонтьевского типа

Пусть L , M - квадратные матрицы порядка n , такие что det L = 0 , а матрица M ( L , p ) -регулярна ( p = 0, n — 1) . Для постановки начально-конечной задачи обычно применяются спектральные проекторы [9-14], которые задаются с помощью контурных интегралов. Однако в конечномерном случае такое задание матриц-условий можно упростить. Именно, представим матрицу P из леммы 1 в виде суммы двух матриц P = P _o + P _r, причем эти матрицы P _o, P описывают проекторы в R ” , т. е. обладают теми же свойствами, что и матрица P . С помощью этих матриц задаются начально-конечные условия

P _o( x (0) — x ₀) = 0,     P t ( x ( T ) — x t ) = 0                         (7)

Сагадеева М.А., Фаткуллина Л.М.

Уфимцева О.В.

с x ₀, x_T е R n описывающие желаемые значения в начальный и конечный моменты времени для нестационарной системы леонтьевского типа

Lx ( t ) = a (t ) Mx ( t) + f ( t ),                                   (8)

где a : [0; T ] ^ R + - скалярная функция, описывающая изменение во времени параметров взаимовлияния значений исследуемой системы, вектор-функция f : [0; T ] ^ R n описывают внешние воздействия на систему. Отметим, что аналогично матрицам P , P существуют соответствующие им матрицы Q_o , Q_T , для которых также выполнено равенство Q = Q_o + Q_T для матрицы Q из леммы 1.

Определение 3. Решение x е C 1 ([0, T ]; R n ) уравнения (8) назовем решением начальноконечной задачи (7), (8), если оно дополнительно удовлетворяет этому условию (7).

Сформулируем теорему о виде решения начально-конечной задачи для нестационарной системы леонтьевского типа.

Теорема 2. Пусть матрица M обратима и (L, p) -регулярна (p = 0, n — 1), а функция a е Cp+1([0, T]; R+ ). Тогда для любой вектор-функции f :[0; T] ^ Rn, такой что Qf е C([0;T];Rn) и (En — Q) f е Cp+1([0;T]; Rn), а также для любых значений x0, хТ е Rn существует единственное решение x е C 1([0, T]; Rn) начально-конечной задачи (7), (8), кото- рое имеет вид

t

х — ¹

х

k

(f

T

X —1

k

^{x (} t ) = lim x k ⁽ t ) = lim k ^^        k ^^

-

p

L

-

L

P 0 ^x 0 ⁺

L

-

L

P^xy +

Z M — E n

-

q = 0

V

V

V

VV

VV

t

t

t

tt

+ i L_/; M i a ⁽ r ) dr 0 ^V     k S

—

X —1

X

k

— 1

L

V

L — ¹ M I Q „ f ( s ) ds

k7

—

T ( '

t

i | l — 1 M f a ( r ) dr

t V V     k S         7

V

L — ¹ M

— 1

X p+1 V

X

k

L

X —1

X

k

— 1

q

L

M

L

— 1

L — ¹ M I Q i f ( s ) ds

k 7

E n

-

L — ¹ M

— 1

V

V

k

—

X p + 1V

L

1 d

q

f ( t )

V a ( t ) dt 7 a ( t )

. (9)

Справедливость данного утверждения следует из применения теоремы 1 к задаче (7), (8).

В теореме 2 через x ( t ) обозначено точное решение задачи (7), (8), а через x_k ( t ) - приближенное численное решение этой задачи.

Следствие. Пусть выполнены условия теоремы 2, тогда приближенное решение x_k ( t ) начально-конечной задачи (7), (8) сходится к точному решению x ( t ) этой задачи, причем выполнено неравенство ||x_k ( t ) — x ( t )|| <  const/ k .

Доказательство. Для того, чтобы показать справедливость данного утверждения, представим решение (9) в виде x ( t ) = x ¹ ( t ) + x ² ( t ) + x ³ ( t ) + x ⁴ ( t ) + x ⁰ ( t ) , где x^l ( t ) - предел соответствующего слагаемого из (9). Покажем сходимость каждого из слагаемых x_k ( t ) ( i = 0,1,2,3,4 ).

При достаточно больших k для первых двух слагаемых решения имеют место неравенства II x k ( t ) — x 1( t )|| <  C 1 / k ,   || x k ;( t ) — x ²( t )|| <  C ₂/ k   ( С_х , С ₂ не зависят от k ),

Математика

которые справедливы в силу результатов из [21] для аппроксимации матриц разрешающих полугрупп. Аналогично для третьего и четвертого слагаемого, используя оценки интегралов и результатов о сходимости из [21], получим неравенства вида

||xk (t) - x3 (t)|| ^ C3 lk , 1x4 (t) - x4(t)|| ^ C4/k , где C3, С4 также не зависят от k. Последнее слагаемое в решении также подчинено подобной оценке.

В силу всех этих оценок мы получаем утверждение следствия.

Заключение. В дальнейшем планируется применить полученные результаты при исследовании конкретных моделей леонтьевского типа, а также для проведения вычислительных экспериментов. Кроме того, в дальнейшем можно будет перейти к исследованию многоточечных начально-конечных условий для систем леонтьевского типа.