Численное решение начально-краевых задач для уравнения теплопроводности методом интегральных уравнений

DOI:

При численном исследовании процессов удаления влаги из влагосодержащих материалов электромагнитным излучением возникает необходимость решения начально-краевых задач для уравнения теплопроводности при различных краевых условиях. Для некоторых тел канонической геометрии удается получить аналитическое решение [1–3]. Для областей произвольной формы предлагается численный алгоритм, основанный на использовании функции Грина оператора Лапласа.

Рассмотрим твердое тело с постоянным коэффициентом температуропроводности a и действующими внутри источниками тепла с заданной плотностью f ( M , t ).

Температурное поле внутри тела определяется решением начально-краевой задачи [7]:

A T -

1 d T a d t

< T|_S =ф ( M , t\ M e S ,

T(M,0) = v(M), M e V, здесь S – поверхность тела; V – объем.

Запишем уравнение в виде:

A T = f +¹ — = F a d t

.

Пусть известна функция Грина G ( M , t ) оператора Лапласа для области V (способ приближенного построения этой функции будет указан ниже).

Тогда решение уравнения представимо в виде [7]:

T ( M , t ) = - 1- J f ( N , t ) G ( M , N ) dV_N - 1- Ы N , t )| G ( M , N ) dS 4 п V                    4 n S      d n_N

N .

Подставляя сюда вместо F ( M , t ) его значение из (2), получаем:

T ( M , t ) +-1- J^ T ( N , t ) G ( M , N ) dV_N =- 1- J f ( N , t ) G ( M , N ^dlV_N 4 n a V d t                      4 п V

—

—

± О n , t )| G ( M , N ) dS_N = g ( M , t ). 4 n S       6 n_N

Уравнение (3) есть интегро-дифференциальное уравнение, описывающее температурное поле T ( M , t ) в объеме V . К нему необходимо добавить начальное условие T ( M , 0) = ψ( M ).

Особенностью уравнения является независимость ядра интегрального оператора от времени и его симметрия, что позволяет применить для построения решения теорему Гильберта – Шмидта [4]. В соответствии с этой теоремой решение и правую часть уравнения представим в виде разложения по собственным функциям f_k ( M ) интегрального оператора, порождающего уравнение (3):

T ( M , t ) = £ C k ( t ) f_k ( M ) , g ( M, t ) = X a k ( t ) f k ( M ) ,

где f_k ( M ) – нормированное решение уравнения:

f ( M ) = x f f ( N ) G ( M , N ) dV_N .

V

Подставляя (4) в (3), получим:

^ C k ( t ) f k ( M ) + 1- ^ dC k T t ) f f k ( N ) G ( M , N ) dV N = k               4 n a k dt v

= 2 ak (t)fk (M),

k где                           ak (t ) = J g (N, ‘)fk (N)dVN = al‘)+ «It),

V ak1 (‘ ) =    HN, ‘ fN) dSN

^{4 л} k л S        5 n N      ^,

^ (t ) = 71" j f ( N , ‘ ) f k ( N >n 4 л k n V                    ^.

В силу линейной независимости системы собственных функций f_k ( M ) имеем:

c k ^{( t )+} '     dc , ^{( t} ) = a k ^{( t} ) или

4Л k na dt dc^ (t)+4л k nack (t ) = 4л k n aak (t),

C k ( 0 ) = b k = J v ( N ) f_k ( N>_N . V .

Решение этой задачи Коши представимо в виде:

c_k ( t ) = 4 Л _k n a J a_k ( t ) D ( t - t ) d т + d_ke ^{- 4X} k ^{a n} t . 0

Удовлетворяя начальному условию, имеем d_k = b_k . Здесь D ( t ) – импульсная реакция дифференциального оператора, определяемая решением задачи Коши:

( t ) + 4 nX_k aD = 0 dt            ^k ,

D ( 0 ) = 1 ,

D ( t ) = e " 4 ^nX k ^at .

Подставляя найденные c_k ( t ) в (4), получим окончательный вид решения:

t

T ( M , t ) = 4n a^fk ( M ) Л_к J a_k ( т ) е ^{- 4 л} k ⁿ a ⁽ ‘ ^-t) d т + be ^{- 4 л} k ⁿ at L

где

ak(t) = J g(N, ‘)fk(N)dVN = ak(‘)+ ak (t), V bk =Jv(N)fk (N>N .

V

Для построения решения по этой формуле необходимо знание функции Грина G ( M , N ), собственных функций f_k ( M ) и собственных чисел λ _k .

Приближенное построение функции Грина

По определению функции Грина задача Дирихле для уравнения Лапласа в области V , ограниченной поверхностью S , имеет вид [7]:

G ( M , N ) = — + U ( M , N )

r MN             ,

G ( M , N ) = 0 при N e S ,

A U ( M , N ) = 0 .

Задача построения G ( M , N ) заключается в отыскании гармонической в V функции U ( M , N ), обеспечивающей выполнение граничного условия G ( M , N) = 0, при N e S.

Эту функцию можно построить приближенно в виде наложения полей нескольких источников, расположенных за пределами области V . Выбор их положения во многих случаях может быть сделан настолько рациональным, что необходимое число источников будет сравнительно мало.

Будем искать функцию Грина в виде:

Г                       ^

G (M, N ) = — + -с1- + -с2- +... + -с-v        r       r             V , rMN ^ rM 1N rM2N        rMnN J здесь Mi – точки расположения источников вне V; ci – мощности источников.

Совмещая точку N последовательно с граничными точками Q_i , i = 1, 2 … m , потребуем выполнения граничного условия:

G ( M , Q i ) = 0, i = 1, 2... m .

Эти соотношения задают систему алгебраических уравнений относительно c_i :

	a ll	a 12	Л	a 1 n		Г C i 1		■ b i "
	a 21	a 21	Л	a 2 n		c 2		b 2
	M	M		M		M		M
	. a m 1	a m 1	Л	a mn .		. c n .		L b m J
где	aij	= 1 r Q i M	, b i	=—, M e V . r MQ i

Заметим, что при m >  n система не совместна, тогда ее можно решить приближенно, например, методом наименьших квадратов [6]. Для исключения такого случая целесообразно положить n = m , в результате получим систему с квадратной матрицей. Такой способ вычисления функции Грина можно рассматривать как распространение метода электростатических изображений [8] на области произвольной формы.

Второй способ приближенного построения функции Грина оператора Лапласа основан на использовании потенциала двойного слоя. Гармоническую в области функцию U ( M , N ), входящую в выражение для функции Грина:

G ( M , N ) = — + U ( M , N )

rMN             , можно искать в виде потенциала двойного слоя:

u ( M , N ) = 1- fT Q k^— dS_e ^{4 П} S     ^d n Q r NQ     .

Удовлетворяя граничному условию:

U m ( M , N )

N e S M e V

rMN

N e S

M e V

и используя свойства потенциала двойного слоя, получим интегральное уравнение:

т ( N ) - -1-f t ( Q )-^— dS Q = 2_ N е S , M е V

4п S     dnQ rNQ       rMN                , здесь n – внешняя к S нормаль.

Для каждой точки M е V , необходимой для дальнейшего использования функции Грина G ( M , N ), решается это ИУ и вычисляется функция Грина.

Если решение искать в виде потенциала простого слоя:

U (M, N ) = — f52 dSt 4тг г п S rNQ

Q ,

то приходим к интегральному уравнению первого рода:

{^ Q ) dS Q =—L, N е S , M е V

.

S r NQ          r MN

Вычисляя приближенно интеграл по формуле прямоугольников, получим:

f

S

^ dS Q = ^ r NQ           i

f a Q dS Q ^i f dS Q =

A S i ' NlQ            i A S i r N k Q

, к = 1,2... n r MN_k

Эти соотношения задают систему линейных алгебраических уравнений (СЛАУ) относи- тельно σ : г

E ^a i a ik = , a ik = J dS Q , k = 1,2... n ^.

i               r MN k          A S i r N k Q

Из-за наличия особенностей 1 r_{N Q} диагональные элементы матрицы этой СЛАУ превосходят остальные, поэтому определитель СЛАУ не равен нулю и она разрешима и при этом единственным способом.

Синусоидальный режим

Пусть все функции, входящие в (3), изменяются во времени по синусоидальному закону. Тогда сопоставляя им комплексные амплитуды, отмеченные точками, получим:

T & M ) +x f T & N ) G ( M , N ) dV_N = g ( M ) ,                         (6)

V i ® где X =----; to - частота,

4 n a

g ( M ) = - 1- f ( NN ) G ( M , N ) dV N -U N )| G ( M , N ) dS N .

4 п V                   4 n S     d n_N

Представляя 2& ( M ) и ^& ( M ) в виде разложений по собственным функциям ядра и подставляя эти разложения в (6), получим:

^ C k f k ( M ) + ^A & f k ( M ) - £ D k f k ( M ) = 0.

k                k ^X k               k

Отсюда имеем:

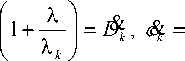
D k

( 1 л 1+ А

где

V ^X к >

D k = J 5M ) / к ( M ) dV M = D'¹ + D k ²⁾, V

5 = ZT" ИN)^fk (N Ш , 4nXk S     оn k = ZT" /N)fk (N) dVN.

^{4 nX} к V

Подставляя найденные 5 в решение, получим:

TM)=2   ; /к (M)=2 I#'"8 / (M).

к 1+—        к х к

Соответствующая временная функция имеет вид:

T ^{( M} , t ) = 2 Wk ^{( M ) si}n ⁽® t ⁺ arg ⁵ )• k

Решение задачи при краевых условиях Неймана

Пусть в задаче (1) краевые условия имеют вид:

^ ( M , t ) о n

= ф ( M , t ), M e S

M e S

Решение этой задачи может быть выражено через функцию Грина задачи Неймана [8]:

T ( M , t ) = - J F ( N , tG N ( m M , N ) dV N - W\T r - ( N , t'G N ( m M , N ) d? N + 4 п V                        4 n a V d t

+ 2 ^ф( N , t 'G N ( M , N ) dS_N ,

4n S где

G^N ( M , N ) = — + U ( M , N ), r MN

A U ( M , N ) = 0,

^ G -( M , N ) = 2, N e S • d nN ^{v 7}   4n S

Эта функция определяется с точностью до слагаемого с ₀( M ), зависящего от положения точки M .

Нормирующее условие J G N ( M , N ) dS N = 0 определяет функцию G N ( M , N) однозначно и де-

S лает ее симметричной [8]. Интегро-дифференциальное уравнение, аналогично (3), имеет вид:

T(M,t)+1- f^T(N,tG (M,N)dVN = - 1- [f (N,tGN (M,N)dVN 4naV dt                       4п V f Ф

Интегральный оператор, порождающий это уравнение, является самосопряженным в классе интегрируемых с квадратом функций и для решения уравнения применима теория Гильберта – Шмидта. Повторяя выкладки, изложенные выше, решение можно записать в виде:

t

to

T(M, t) = £ fk (M) 4naXk J ak (t)e-xk't-t)dт + bke-4Xknat k=1

bk = Jv(N)fk (N) dVN, V ak = ak(t)+ ak(t),

fT( N, t)fk (N) dSN, 4nXt kS

—     Jf (N, t)fk (N) dVN

^4nXk V

К (N), X k – решение уравнения f (M )=XJ f (N "GN (M, N >N,

V нормированное условием

J f (N )dS_N = 0.

S

Приближенное построение функции Грина задачи Неймана

Как и ранее, функцию Грина G^N(M, N) будем искать в виде:

GN(M, N) = — + -^- + с²^ +... + с²^ + c₀(M), N e V rMN   rM₁N   rM₂N       rM_nN

Здесь c₀ – постоянная, зависящая от точки М, с точностью до которой определяется G^N(M, N). Эта постоянная однозначно определяется нормирующим условием:

J GN (M, N)dSN = 0, S c о(M ) = - ^f — SS rM,

n

+z c^

k=1 rM_tN

dSN

Подставляя G^N(M, N) в граничное условие:

dG^N     „ x 1

-----(M, Q ) =--, dn_o^{v     7} 4nS

Qi

Q, e S, i = 1,2K m, i

получим СЛАУ относительно c_k. В матричном виде эта СЛАУ имеет вид:

a₁₁

a₂₁

М

a₁₂

a₂₁

М

л

л

a1n a2n

М

•

ci c2

М

а 1 m1

а 1 m1

л

а mn

cn

b b2

М . bm .

д aij =----- дnQi

\

I rQMJ

,

bi =

-

д

/

1 )

-

дп,

’ Qi I ^rMQ J

4п5^.

Подстановка найденных c_k и c₀в (8) дает приближенное значение функции Грина задачи Неймана для уравнения Лапласа.

Приближенные значения собственных функций fk(M) и собственных чисел X _к интегральных операторов с ядрами G(M, N) и G^N(M, N) можно построить методом Келлога [4]. Другой способ вычисления собственных функций и чисел заключается в замене в (5) интеграла квадратурной формой (например, прямоугольников). При этом задача отыскания собственных функций и чисел сводится к алгебраической проблеме вычисления спектра симметричной матрицы, которая может быть решена методом спектрального разложения матрицы [6].

Из формул (6) и (7) следует, что искомое температурное поле T(M, t) определяется только собственными функциямиf(M) и числами Xк удовлетворяющими уравнению (5). Известно [8], что решение (5) эквивалентно решению задачи Штурма – Лиувилля:

Af + Xf = 0, f (M ) M ., = 0.

Эту задачу можно приближенно решить методом, аналогичным методу построения функции Грина G(M, N), изложенному выше.

При положительных X фундаментальное решение уравнения (8) имеет вид [7]:

R (M, N )= n'^Xr") r_MN

.

Вне области решения Vвыберем произвольно точки Ni, i = 1,2...п и расположим в них источники мощностью c_i. Решение уравнения (8) представим в виде наложения полей этих источников:

f (M, N )-£ s^n|'^;rMNi)

.

i=1

rMN_i

Последовательно совмещая точку M c граничными точками Qi, i = 1,2...п и приравнивая результат к нулю, получим однородную СЛАУ с симметричной матрицей A = (a_ij), где

а aij

sin ⁽7XrM .Ni.)

,

rMjNi

ненулевое решение этой СЛАУ существует при условии det(a_ij) = 0. Корни этого уравнения есть искомые собственные числа Xк. Метод решения этого уравнения и вычисления собственных функций изложен в [5].

Заметим, что при таком способе определения собственных чисел и функций не требуется предварительного вычисления функции Грина G(M, N), что сокращает объем вычислений.

Для областей, границы которых совпадают с координатными поверхностями каких-либо ортогональных координат, собственные функции и числа легко построить методом Фурье [7].