Численное решение нелинейного уравнения Шредингера в декартовой системе координат

Как известно [1], нелинейное уравнение Шре-

Без учета нелинейных эффектов уравнение Шредингера принимает вид

дингера является частным случаем волнового уравнения в параболическом приближении, записанном с учетом эффекта самовоздействия. Эффект самовоз-

д U

---+ дz

i

2 кп ₀

Л D U = 0

действия проявляется при распространении оптического излучения в средах с кубичной нелинейностью (поляризация пропорциональна напряженности электрического поля в третьей степени).

С учетом этого эффекта уравнение Шредингера в декартовой системе координат запишем как [1]

В дальнейшем уравнение (1) будем называть нелинейным уравнением Шредингера, а уравнение (3) - линейным уравнением.

д и i , +    Л d д z   2 кп 0	и + 1кпн: и 2 и = 0, (1) 2 п 0
- L x <  x < — 22	LL , -    <  y <     , 0 <  z <  L ,
где Ло = Л + Л = xy	Г д 2 ^д 2 )        _ п = 1 —-+--- 1 - оператор Лапла- (д x 2 д y 2 J

1. Расчетная конечно-разностная схема с итерационным уточнением

Для численного решения системы (1) - (2) построим разностную схему Писмена-Рэкфорда [2]. Определим сетку zk = к ■ h,, к = 0, K, h, = L / K kz    z

са в декартовой системе координат,

U - напряженность электрического поля, k - волновой вектор,

По - показатель преломления среды, пнл - изменение показателя преломления под действием поля распространяющейся волны.

Отметим, что ось Z совпадает с направлением распространения волны, а оси X и Y лежат в плоскости, перпендикулярной оси Z .

Для получения замкнутой краевой задачи дополним уравнение (1) следующими краевыми условиями

x i = i ■ h_x , i = - 1 /2, I /2, h_x = L_x 11

y - = - ■ h . , - = - J /2, J /2, h . = L y I J h z , h_x , h_y - шаги дискретизации по переменным z, x и y .

Обозначим через и к сеточный аналог численного решения и ( x i , y - , z_k ) .

Оператор Лапласа аппроксимируем следующим разностным оператором [2]:

Uk hx hxk '

1V x   ij

Ц + ик+ hx2

x

.

Задаче (1)-(2) поставим в соответствие следующую двухслойную нелинейную разностную схему:

и к. + ^1/2 ij

U z = 0 = ^{ф (} x , У )

Hx- L x ,2 = ⁰

Ч = L x /2 = 0 .                           (2)

^U|, - L y ,2 = ⁰

_ Д = L . ,2 = ⁰

Функция ф ( r ) описывает напряженность электрического поля волны на входе в среду (волновод), а нулевые граничные условия показывают, что среда (волновод) ограничены проводящей оболочкой.

0,5 h_z

и^{к + 1} ij

^ик ₊   i

2 кп ₀

ikn ² I

। нл

2 п 0

U к. + ^1/2 ij

0,5 h_z

к +л и к ) +

| ик ^{+ 1/2}|² и к ^+1/2 = 0

i

+

2 кп ₀

,к * ^|/2 +Л> к ⁺ ) + (4)

, ^iknнл к кк + 1/2 I² _ткк + 1/2 _ _п

⁺ 2 п ₀ ^иу ।         = ⁰

и - = ф ( r )

^и — I /2 - = ^ик /2 - = ^ик- J /2 = ^иУ /2 = ⁰

Первое уравнение системы разностных уравнений (4) является нелинейным. Для нахождения неиз- k + 1/2

вестной функции U _ij можно использовать итерационный метод последовательных приближений в сочетании с разностной прогонкой по x и y :

5 + 1 k + ¹/² U ij

^^^^^^в

0,5 h_z

^Ui^kj        i

+ 2 kn ₀

( „ 5 + 1 ^{k +1/2} Л h x U ij

I

■ ^{л u}

+

2.1. Результаты экспериментальных исследований линейного уравнения

Пучок, описываемый формулой (7), является стационарным, так как | U ⁽ x , y , z ) = \U ⁽ x , y ,0 ) , то есть распределение интенсивности в плоскости OXY не зависит от расстояния z . Это распределение изображено на рис. 1.

+ ik'i

2 n ₀

₅ k + 1/ 2

U ij

² 5 + 1

k + 1/2

U ij = 0

,

(5),

₀ k + 1/2 причем U ij = U k .

5 + 1

Таким образом, система (4) примет вид: k + 1/2

U ij

^^^^^^в

0,5 h_z

U ik + i

2 kn ₀

( „ 5 + 1 ^{k + 1/2} Л ^ U ij

I

^ + A h U

+

Рис. 1. Распределение интенсивности волны в линейной среде.

На рис. 2-4 приведены результаты численного решения линейного уравнения Шредингера на различных расстояниях от входа в среду.1

Для проведения численных расчетов были использованы следующие значения параметров:

L _x= L _y =50 мкм;

X =0,63 мкм, причем X =2 n /k;

n 0 =1.

<

U ^{k +1} ij

^^^^^^в

₊ ^ikn2л 2 n ₀

₅ k + 1/ 2

U ij

² 5 + 1

k + 1/2

U ij = 0

k + 1/2 ij

0,5 h_z

i

+

2 kn ₀

k +² +Л h y U k ⁺¹ ) +

U j = Ф r )

₊ ^л

2 n ₀

Uk ^

1² U * ^+1/2 = 0

₀ k + 1/2

U ij    = u *

^U — kl /2 j = U I /2 j = ^Uik - J /2 = ^Uik /2 = ⁰

В ходе теоретических исследований удалось доказать, что схема (6) имеет порядок аппроксимации Oh², h y , h z ^{) .}

В результате проведения вычислительных экспериментов получено подтверждение сходимости разностной схемы (6). Процесс итерационного уточнения обнаружил быструю сходимость: для уточнения решения до величин порядка 10-4 требуются 2-3 итерации.

Рис. 2. Распределение интенсивности волны на расстоянии L от входа в среду (L = 100 мкм, nz = 1000, nx = 70, ny =70).

2. Вычислительные эксперименты для среды с постоянным показателем преломления

Рассмотрим сначала аналитическое решение линейного уравнения.

Будем решать линейное уравнение методом разделения переменных. В этом случае одно из частных решений задачи (1) –(2) запишется в виде

(

U ( x , y , z

2   „2 7

) = exp ⁱ²| r ■ y r -     '

V V

x

'^y ; ;

n x | . — I sm

L

x

Г „ A ny

L"

V ^y 7

,

Рис. 3. Распределение интенсивности волны на расстоянии L от входа в среду (L = 500 мкм, nz = 5000, nx =70, ny =70).

где ^a =      ,

2 kn ₀

а начальное условие

sm

Г ny

T"

V ^y 7

1 В дальнейшем использованы следующие обозначения: nx, ny, nz- количество интервалов разбиений по осям x, y и z соответственно.

Рис. 4. Распределение интенсивности волны на расстоянии L от входа в среду

(L = 1 мм, nz =5000, nx = 70, ny = 70).

Из приведенных рисунков видно, что на расстояниях порядка миллиметра распределения интенсивности волны, полученные с помощью численного решения уравнения Шредингера практически совпадают с аналитически рассчитанным распределением. Среднеквадратическая ошибка при этом не превосходит 5%.

3.2. Численное решение нелинейного уравнения Шредингера

Самофокусировка пучка

На рис. 5-7 приведены результаты численного решения нелинейного уравнения Шредингера сосле-дующими параметрами:

L _x= L _y = 50 мкм;

X = 0,63 мкм, причем X =2 n /k;

n о =₂ 1;

n _нл =0,001, причем n _нл >0.

Рис. 5. Распределение интенсивности волны на расстоянии L от входа в среду (L = 100 мкм, nz = 1000, nx =50, ny = 50).

Рис. 6. Распределение интенсивности волны на расстоянии L от входа в среду

(L =300 мкм, nz = 5000, nx = 50, ny = 50).

Рис. 7. Распределение интенсивности волны на расстоянии L от входа в среду

(L = 500 мкм, nz = 10000, nx =50, ny = 50).

В работе [1] показано, что при пнл >0 происходит фокусировка пучка, то есть смещение энергии пучка к центру. Это явление можно наблюдать и на рисунках 5-7.

Самодефокусировка пучка

На рис. 8-11 приведены результаты численного решения нелинейного уравнения Шредингера со следующими параметрами:

L _x= L _y = 50 мкм;

X = 0,63 мкм, причем X =2 n /k;

n 0 = 1;

n _нл² =0,001, причем n _нл<0.

Рис. 8. Распределение интенсивности волны на расстоянии L от входа в среду (L =200 мкм, nz = 1000, nx = 50, ny = 50).

Рис. 9. Распределение интенсивности волны на расстоянии L от входа в среду (L =500 мкм, nz = 1000, nx = 50, ny = 50).

Рис. 10. Распределение интенсивности волны на расстоянии L от входа в среду

(L = 800 мкм, nz = 1000, nx = 50, ny = 50).

Таким образом, A ( z ) = K exp l i

Преобразуя (11), получаем

-¹ Л x^B + ^fn 0 = B

- C ^Л y C = g 2 ,

где g ² - произвольная константа.

С учетом (13)

^C = s^{in (} yg ) .

Представим B ( x ) функций

r

B ( x ) = X ( x ) exp

^^^^^^B

в виде произведения двух

Рис. 11. Распределение интенсивности волны на расстоянии L от входа в среду

(L = 1000 мкм, nz = 1000, nx = 50, ny = 50).

В работе [1] показано, что при n нл <0 происходит самодефокусировка пучка в нелинейной среде, то есть смещение энергии пучка в периферийную зону. Приведенные выше графики численного моделирования демонстрируют этот факт.

V

x 2

'X ..

.

После подстановки (15) и (9) в (13), и осуществив замену переменных, получаем

X ( x ) = H n

V ® 0 )

где H N – многочлен Эрмита, причем

2 N = ( fn 1 - g 2 ) ^ 2^L - 1,

2      2 ^a

®0 = R”T '

V fn 1A

Таким образом, с учетом (15), (14), (12) и (9) получаем искомое решение

r. f

U ( x , y , z ) = K exp l i ту z I Sin ( yg ) H n V 2 k )

( RA xn 2

x

r x exp

^^^^^^B

3. Вычислительные эксперименты для среды с показателем преломления, распределенным по параболическому закону

V

x ²

.„2 ® 0 J

.

( ®0 J

V 7      (19)

Пусть показатель преломления зависит от координаты x следующим образом

3.1.Результаты численного решения линейного уравнения Шредингера

n 0 = n 1

Г            2

1 - 2 a[ - I

V a )

Для вычислительных экспериментов выберем, например, моду Гаусса-Эрмита с номером N =11.

,

Для выполнения граничного условия необхо-

V

причем n нл = 0.

Заметим [3], что при x < a

димо, чтобы H_N

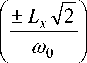
= 0 . Пусть, например,

n о = n 1

Г ,

1 —A

V 1

x

a

2 ^

Будем искать решение уравнения в виде

U ( x , y , z ) = A ( z ) B ( x ) C ( y ) .                  (10)

Подставляя (10) в уравнение (1), получаем факторизованное уравнение

2 ik d A

T 'a z

—I— Л, B +—Л C = — f , n ₀ V в       C y )

где f - произвольная константа.

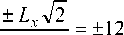
® 0

так как H N ( ± 12 ) ® ± 10 ¹⁶ .

Для выполнения граничного условия при y = L y получаем

п g=т

Ly

.

Из (17) и (18) можно найти f и p = Д- a2

На рис. 12 изображено распределение интенсивности в пучке, описываемом формулой (19).

На рис. 13 - 14 приведены результаты численного моделирования линейного уравнения со следующими параметрами:

R = 50 мкм;

X = 0,63 мкм, причем Х =2 п / к ;

n 1 = 1.

Как видно из приведенных графиков, результат численного решения уравнения Шредингера практически полностью совпадает с результатом аналитического решения.

Рис. 12. Распределение интенсивности волны в линейной среде.

Рис.13. Распределение интенсивности волны на расстоянии L от входа в среду (L=1 мм, nz =1000, nx = 80, ny = 80).

Рис.14. Распределение интенсивности волны на расстоянии L от входа в среду (L = 10 мм, nz =50000, nx = 80, ny = 80).

Заключение

Проведенные исследования подтвердили высокую точность численного решения задачи на расстояниях порядка миллиметра. Так для модели среды, не учитывающей эффект самовоздействия, численное решение практически совпадает с аналитическим, рассчитанным по формуле (7).

Для среды с “параболическим профилем” показателя преломления моды Гаусса-Эрмита, рассчитанные с помощью схемы (6), практически не претерпевают изменений в процессе распространения волны на расстояния порядка десятков миллиметров, что соответствует теории [3].

Для модели среды, учитывающей эффект само-воздействия, численный расчет позволяет наблюдать как явление самофокусировки излучения, так и его самодефокусировки, что спрогнозировано теоретическими оценками, например, в работе [1].