Численное решение нелинейного уравнения Шредингера в радиально-симметричном случае

Как известно [1], нелинейное уравнение Шредингера является частным случаем волнового уравнения в параболическом приближении и с учетом эффекта самовоздействия. Эффект самовоздействия проявляется при распространении оптического излучения в средах с кубичной нелинейностью (поляризация пропорциональна напряженности электрического поля в третьей степени).

С учетом этого эффекта уравнение Шредингера в радиально-симметричном случае запишется как [2]

д U i , — + ——Л _rU

дz 2 kn ₀ 0 <  r <  R ,

- kn^ U ² U = 0, 2 n 0

0 <  z <  L ,

где Л _r

Г д ²

1 д)

--Г +---

^д r ² r д r ^

- оператор Лапласа в ради-

ально-симметричном случае,

U - напряженность электрического поля, k - волновой вектор, n о - показатель преломления среды, n _нл - изменение показателя преломления под действием поля распространяющейся волны.

Уравнение (1) необходимо дополнить граничным и начальным условиями

zk = k ■ hz, k = 0, K -1, hz = LIK kz      z ri = (i + 0,5) ■ hr, i = 0, I -1, hr = R I( I + 0,5), где hz, hr - шаги по переменной z, описывающей направление распространения волны, и по радиальной переменной соответственно.

Оператор Лапласа по переменной r аппроксимируем следующим разностным оператором [3]:

Л , A ( r ) = 4- ( r + 0.5 h r ) A ^{( r +} h r ¹ - A ^{( r} ' - rh_r                     h_r

1 ( n C1 a A(r)- A(r - hr) (r - 0.5hr)---------------------, rhr           r          hr причем Л r =Л rA + O(hr21 r) для достаточно гладкой функции А. Задаче (1)-(2) поставим в соответствие следующую двухслойную нелинейную разностную схему:

I a" h z • r ^)- a ^{( z} ■ r ) + -L- л A ( z , r ) - h z             2 kn 0 ^{r !}

■              - kn^ |A ( z , r )|² A ( z , r ) = 0        ⁽⁴⁾

2 n 0a (0, r) = ^( r)

a ( z , R ) = 0

A ( z , r ) = 0.5 ( a ( z + h_z , r ) + a ( z , r )) .

^U\z =0 = ^{ф (} r )

U r = R = 0

<

Функция ф ( r ) описывает напряженность электрического поля волны на входе в среду (волновод), а нулевые граничные условия показывают, что среда (волновод)ограничены проводящей оболочкой.

Без учета нелинейных эффектов уравнение Шредингера принимает вид

Система разностных уравнений (4) является нелинейной. Для нахождения неизвестной функции a ( z + h_z , r ) можно использовать итерационный метод последовательных приближений в сочетании с разностной прогонкой по r:

5+1/ a (z + hz, r)- a (z, r)

дU    i . п

--1--Л _rU = 0

дz   2 kn ₀

В дальнейшем уравнение (1) будем называть нелинейным уравнением Шредингера, а уравнение (3) - линейным уравнением.

1. Расчетная конечно-разностная схема с итерационным уточнением

Для численного решения системы (1)-(2) построим консервативную разностную схему [2]. Определим сетку

hz

s

2 s

i           ^s +1

+ y—^Л r A ^{( z} , ^{r )} 2 kn 0

--нл- A ( z , r ) A ( z , r ) = 0, ^{2 n} 0

< a ( z + h_z , R ) = 0,

"A ( z , r ) = 0.5 | a ( z + h z , r ) + a ( z , r )|,

a ( z + h z , r ) = u ( z , r ),   5 = 0,1,...

Теоретические исследования сходимости схем вида (5) приведены в работе [2].

Необходимо также отметить, что так как данная схема является консервативной, она - аналог интегральной формы закона сохранения электромагнитной энергии в среде.

2. Вычислительные эксперименты для среды с постоянным показателем преломления

Рассмотрим сначала аналитическое решение линейного уравнения, то есть п нл = 0. В этом случае решение задачи (1) запишем в виде

На рис. 2-3 приведены результаты численного решения линейного уравнения Шредингера на различных расстояниях от входа в среду.1

В расчетах были использованы следующие значения параметров:

R =50 мкм;

X =0,63 мкм, причем Х =2 л /к;

n 0 =1.

«

U(z, r)= Е Cm exP m =0

2     1

i "

R 7

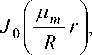
где ^a = -^T~ , 2 kn ₀

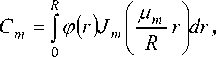
а ^ _m - нули функции Бесселя нулевого порядка.

Для простоты выберем начальное условие в виде функции Бесселя нулевого порядка

^{ф (} r ) = J о

f * r 1

V R 7

тогда, используя свойство ортонормированности Бесселевых функций, получаем

C 0 = 1, C m = 0, m = 1,2...,

в результате решение системы (1) - (2) будет иметь вид

f

U ( z , r ) = exp

V

„ 2 1

i     ^{0 2} J'

R 7

f ^ 1 r 1 .

V R 7

2.1. Результаты экспериментальных исследований линейного уравнения

Пучок, описываемый формулой (6), является стационарным, так как | U ( r , z ) ² = | U ( r ,0)| 2 , то есть распределение интенсивности в плоскости OXY не зависит от расстояния z . Это распределение изображено на рис. 1.

Рис. 2. Распределение интенсивности волны на расстоянии L от входа в среду

(L = 1м, nz = 1000, nr = 100).

Рис. 1. Распределение интенсивности волны в линейной среде.

Рис.3. Распределение интенсивности волны на расстоянии L от входа в среду (L = 10м, nz = 1000, nr = 100).

Как видно из приведенных графиков результат численного решения уравнения Шредингера полностью совпадает с результатом аналитического решения. Это подтверждает правильность выбора консервативной разностной схемы (5) для вычислительных экспериментов с уравнением Шредингера.

3.2. Численное решение нелинейного уравнения Шредингера

Самофокусировка пучка

На рис.4-6 приведены результаты численного решения нелинейного уравнения Шредингера со следующими параметрами:

R =50 мкм;

Х =0,63 мкм, причем Х =2 л /к;

¹ В дальнейшем использованы следующие обозначения:

nr - количество интервалов разбиений по радиусу;

nz - количество интервалов разбиений по оси z .

Белым цветом изображается график решения линейного уравнения (3), а серым цветом - график численного решения уравнения Шредингера (1)-(2).

n о = 1;

n нл 2 =0,001, причем n нл >0.

В работе [1] показано, что при nнл >0 происходит фокусировка пучка на расстоянии f = R

n 0

2 n 2 ф ( 0 )

от входа в нелинейную среду.

Рис. 4. Распределение интенсивности волны на расстоянии L от входа в среду (L = 500мкм, nz = 1000, nr = 100).

Подставляя экспериментальные значения параметров, получаем, что f ® 1100 мкм. Вычислительные эксперименты (рис. 3-5) показывают, что фокусировка пучка происходит на расстоянии порядка 800-900 мкм. Таким образом, результаты численного решения достаточно близки к теоретическим оценкам, что еще раз подтверждает практическую пригодность выбранной разностной схемы.

Рис. 5. Распределение интенсивности волны на расстоянии L от входа в среду (L = 700мкм, nz = 1000, nr = 100).

Рис. 6. Распределение интенсивности волны на расстоянии L от входа в среду (L = 750мкм, nz = 1000, nr = 100).

Самодефокусировка пучка

На рис. 7-10 приведены результаты численного решения нелинейного уравнения Шредингера со следующими параметрами:

R = 50 мкм;

X = 0,63 мкм, причем X =2 n /k;

n 0 =1;

n нл ²=0,001, причем n нл <0.

Рис. 7. Распределение интенсивности волны на расстоянии L от входа в среду (L = 500мкм, nz = 1000, nr = 100).

Рис. 8. Распределение интенсивности волны на расстоянии L от входа в среду (L = 1мм, nz = 1000, nr = 100).

Рис. 9. Распределение интенсивности волны на расстоянии L от входа в среду (L = 1,5мм, nz = 1000, nr = 100).

В работе [1] показано, что при n нл <0 происходит самодефокусировка пучка в нелинейной среде, то есть смещение энергии пучка в периферийную зону. Приведенные выше графики численного моделирования демонстрируют этот факт.

Рис. 10. Распределение интенсивности волны на расстоянии L от входа в среду (L = 2,5мм, nz = 1000, nr = 100).

Осуществим еще одну замену переменных

2а а = — to02

Тогда получим

, д2 х         дх а---- + (1 - а')---+ да'2          да'

₊ ®!_ f fn 1

V

^^^^^^»

I

X^х = ⁰ to ₀ 7

Решением уравнения (16) являются многочлены Лагерра

X = L s ( а ') = L s

3. Вычислительные эксперименты для среды с показателем преломления, распределенным по параболическому закону

Пусть показатель преломления зависит от радиуса следующим образом

причем fn 1

s = —¹ to о —

n 0 = n 1

f 2 I

1 - 2 A ^f r 1

V a 7

,

V

причем n _нл = 0.

Будем искать решение уравнения в виде

U ( z , r ) = A ( r ) B ( z ) .                               (8)

Подставляя (8) в уравнение (1), получаем факторизованное уравнение

2 ik 8 B     1 _A ,

--=---Л _rA = - f

B d z   n 0 A

где f - произвольная константа.

f f

Таким образом, B ( z ) = C exp l г —z I .      (10)

V 2 k )

Представим A (r) функций

в виде произведения двух

f

A ( r ) = X ( r ) exp

-

V

r ²

^{to 2} 7

.

После подстановки (11) и (10) в (8) получаем

a ² х 4 r a x

^^^^^^B

a r ² го 0 a r

1 ax + r ar

^^^^^^B

4- ^{x + to} 0

+ — X + fn 0 X = 0

^to 0

Осуществим замену переменных а = r ². Тогда (12) преобразуется к виду

д2 X   , а—у + 1 да2

^^^^^^B

V

2а |дX hx+ to0 ) да

f А

V 4

^^^^^^B

X | ^х + ^го 0 7

+

f а - ^а д /П 1 1 x = 0.

V to 4 4 a ² 7

1     A Ini

Пусть 4 =    2- .

to 0     4 a

^f 2 r ²'

V to ₀ 7

,

Таким образом, с учетом (8), (10) и (11) получаем искомое решение

f f Y f 2 r ² 1

U ( z , r ) = C exp i—z L ——lx exp ^s_m2 I

V 2 k 7 V to ₀ 7

f

2 k

f r ²

^^^^^^B

V ^to 0 ²

3.1. Результаты численного решения линейного уравнения Шредингера

Для вычислительных экспериментов выберем, например, моду Гаусса-Лагерра с номером s=10

Тогда из (18) и (14) получаем, что

_f = 42 2 ^A n ₁ a ²

a ²

to о =

Для того чтобы обеспечить выполнение граничного условия, выберем аргумент многочлена Лагерра, равный десятому нулю функции.

2 R ²

—Г = m 10 , ^to 0 ²

где m 10 =29,9206970123 - десятый нуль многочлена Гаусса-Лагерра.

На рис. 11 изображено распределение интенсивности в пучке, описываемом формулой (19).

Рис. 11. Распределение интенсивности волны в линейной среде.

На рис. 12-13 приведены результаты численного моделирования линейного уравнения со следующими параметрами:

R = 50 мкм;

λ = 0,63 мкм, причем λ =2 π /k;

n 1 = 1.

Рис.12. Распределение интенсивности волны на расстоянии L от входа в среду

(L = 1м, nz = 1000, nr = 100).

Рис. 13. Распределение интенсивности волны на расстоянии L от входа в среду

(L = 10м, nz = 1000, nr = 100).

Как видно из приведенных графиков, результат численного решения уравнения Шредингера полностью совпадает с результатом аналитического решения.

Заключение

Итак, в результате проведения вычислительных экспериментов получено подтверждение сходимости разностной схемы (5), использованной для решения нелинейного уравнения Шредингера. Процесс итерационного уточнения обнаружил быструю сходимость: для уточнения решения до величин порядка 10-4 требуются 2-3 итерации.

Проведенные исследования подтвердили высокую точность численного решения задачи. Так для модели среды, не учитывающей эффект самовоздей-ствия, численное решение практически совпадает с аналитическим, рассчитанным по формуле (6).

Для среды с “параболическим профилем” показатели преломления моды Гаусса-Лагерра, рассчитанные с помощью схемы (5), практически не претерпевают изменений в процессе распространения волны на расстояние порядка десятков метров, что соответствует теории [4].

Для модели среды, учитывающей эффект само-воздействия, численный расчет позволяет наблюдать как явление самофокусировки излучения, так и его самодефокусировки, что спрогнозировано теоретическими оценками, например в работе [1].