Численное решение обобщенных осесимметричных задач динамики упругопластических оболочек вращения при больших деформациях

Обзор работ, посвященных численным решениям осесимметричных геометрически нелинейных задач упругопластического деформирования и устойчивости оболочек при статических нагружениях, представлен в [1], а при динамических — в [2]. Эти публикации в основном посвящены решению задач с малыми деформациями и немалыми перемещениями металлических оболочек. Численный анализ больших безмоментных деформаций гиперупругих оболочек содержится в монографии [3]. Постановки и результаты решения обобщенных осесимметричных упругопластических задач с кручением в литературе отсутствуют. Подобные задачи возникают при действии внутреннего давления и / или растяжения с кручением и характерны для экспериментальных исследований поведения металлических трубчатых образцов при больших деформациях и неоднородном сложном напряженно-деформированном состоянии. Численное решение этих задач в трехмерной постановке малоэффективно, а подчас и невозможно при использовании коротационной производной Яуманна без выделения больших вращений оболочки как жесткого целого, характерных для задач кручения длинных оболочек даже при малых деформациях. Наиболее простым способом численной реализации нестационарных упругопластических задач с большими деформациями является применение метода конечных элементов и явной схемы интегрирования по времени. Последняя позволяет осуществлять пошаговое перестроение геометрии оболочки, причем на каждом шаге по времени фактически рассматриваются линеаризованные кинематические соотношения в метрике текущего состояния. Современные компьютеры дают возможность с приемлемыми вычислительными затратами осуществлять путем прямого интегрирования уравнений движения моделирование процессов деформирования в широком диапазоне скоростей нагружения (от квазистатических до динамических). Отметим, что обзор математических моделей, постановок задач и численных методов решения нелинейных задач динамики оболочек представлен в работах [4–6].

2.    Кинематические соотношения

Обобщенную осесимметричную задачу (с кручением) сформулируем в цилиндрической системе эйлеровых координат O rz , где O z — ось вращения. Для каждого оболочечного элемента введем местную сопутствующую (лагранжеву) систему координат O ’ s S [1]. Здесь: s — длина дуги меридиана оболочечного элемента (0 <  s <  L ); S — координата, отсчитываемая от срединной поверхности оболочки и нормальная к ней ( - h /2 h /2); h = h ( s , t ) — толщина оболочки; t — время. Общая и местная системы координат связаны соотношениями: s = r v z - z v r , S = r у r + z у z , где v z = - r , _s , V _r = z , _s — направляющие косинусы нормали к срединной поверхности, символ «, _s » означает дифференцирование по пространственной переменной s .

Оболочечные элементы полагаем тонкими, изменением метрики по толщине пренебрегаем. Деформации поперечного сдвига и изгиба считаем малыми, а деформации срединной поверхности — большими. Деформации сдвига 8_ps не принимаем во внимание ( в — окружная координата).

Распределение скоростей перемещений по толщине оболочки представим в виде:

U t s ( s , S , t ) = U s ( s , t ) + S «_ф ( s , t ),      U^ ( s , S , t ) = U^ ( s , t ),      U p ( s , S , t ) = r 9 ( s , t ).

Здесь: U_s ( s , t ), U _s ( s , t ) — скорости перемещений срединной поверхности в направлении касательной и нормали; U t ^ ( s , t ) — угловая скорость поворота поперечных сечений в плоскости меридионального сечения; 9 ( s , t ) — угловая скорость поворота относительно оси вращения; точка над обозначением величины означает ее дифференцирование по времени.

Кинематические соотношения запишем в скоростях и построим в метрике текущего состояния, что позволяет учитывать большие деформации и формоизменения оболочки. Распределение компонент скоростей деформаций (симметричной части градиента скорости перемещений) по толщине примем в виде:

8 _н = 8 0 + S ⁸ ИИ     ( i = s , в ),      8 s s =8 0 , (1 - (2V h )²),      8 s p =8 0 p ,                        (1)

где 8 ° — компоненты скорости деформации срединной поверхности, S ^8И — компоненты скорости деформации изгиба.

Компоненты тензора скоростей деформации и скорость вращения гоsр элемента выразим через компоненты обобщенных скоростей перемещений Utr, Utz, U^, 9

• 0      ■             ■            д0 ■ —1    дИ • дИ •        —1    -0 А

• ⁸ss = ^Ur, s V z^{- U}z, s V r , ⁸pp = ^Urr , ⁸ss = U^, s , ⁸pp= ^U„V zr , ⁸_sp= r⁹, s Z^2, 8s°s = (U„ + Utr,sVr + Utz,sVz )/2, bsp = - r9,s /2.

  
  
3.    Физические соотношения

Учет упругопластических свойств материала оболочки (металлы, сплавы) осуществляется в рамках теории течения с нелинейным изотропным упрочнением. Предполагается, что упругие деформации малы, а пластические деформации могут быть большими. Компоненты тензора скоростей деформаций 8 t _ij можно представить в виде суммы упругой 8 e и пластической 8 p составляющих: t j =8 j +8 p , 8 p = 0 ( i , j = s , p , S ).

Компоненты тензора напряжений Коши, нормальные к срединной поверхности оболочки, принимаются равными нулю ( o ^^ = 0). Из этого условия и обобщенного закона Гука определяются компонента 8 Ss , компоненты скоростей напряжений O j и напряжений o j :

8 ^^ =А ( 8 ss +8 p p ), o ss =       ( 8 es_S +p8 p p ),

ц-1               1-ц

e e             E e            E e

^{( 8} pp ⁺ ^ ⁸ ss )’    ^O s p   ,      ⁸ s p ,    ^O s s   .      ⁸ s s ,

1 + Ц           1 + Ц

t

E

^{O pp} 1 -ц ² t

D , ^o u =° ij ^+o jk ^b ki ^+o ik ^b kj  ⁽ i , ^j , ^k = ^s , ^{p )},    O j = J D J ^o ij ^{dt  (} i , ^j = ^s , ^{p )},    ^o s s = j ° s s ^dt ,

0                                               0

где E — модуль Юнга, ц — коэффициент Пуассона, символ DJ означает производную по Яуманну [7, 8], которая учитывает поворот элемента оболочки за счет сдвиговой деформации как квазижесткого целого относительно нормали к её срединной поверхности при кручении. Причем местная сопутствующая система координат О’ 5 ^ обуславливается формоизменениями оболочки без учета сдвиговых деформаций кручения, то есть она является лагранжевой только в случае осесимметричной деформации. Заметим, что деформации сдвига при кручении тонких оболочек ограничены из соображений устойчивости осесимметричного процесса деформирования. Металлические трубки при чистом кручении, как показывают эксперименты, теряют устойчивость при углах закручивания порядка л/12 с образованием неосесимметричных форм. Поэтому введение производной Яуманна для учета квазижесткого вращения при кручении вполне обосновано при использовании явной схемы интегрирования с малыми шагами по времени. В итоге существенно упрощается запись основных уравнений обобщенной осесимметричной задачи с кручением, так как за базовую берется лагранжева система координат осесимметричной задачи.

Скорости пластических составляющих деформации описываются ассоциированным законом течения:

t

• s pp = к с j , с j c j =( 2/3 ) с 2 ( к ), с j =Cy -а8 у , с = (с 55 + C pp )/3, к = 72/3 J VS p S p" dt .         (⁴)

• 4.    Уравнение движения

Здесь параметр к , тождественно равный нулю при упругом деформировании, определяется при пластическом деформировании из условия прохождения мгновенной поверхности текучести через конец вектора догрузки; с , ( к ) — радиус поверхности текучести; к — параметр Одквиста.

Рассмотрим элемент оболочки, ограниченный контурными сечениями 5 = 0, L . Пусть к контурам приложены внешние усилия [ P_r ( t ), P_z ( t ), P p ( t ) ] и изгибающий момент Г M И ( t ) ] Кроме контурных усилий на оболочечный элемент могут действовать нагрузки p_r ( 5 , t ), p_z ( 5 , t ), распределенные по поверхности.

Уравнения движения оболочки следуют из уравнения баланса виртуальных мощностей работы, известного из механики сплошных сред. Учитывая принятые гипотезы теории оболочек, выполняя интегрирование по толщине и пренебрегая силами Кориолиса, получим вариационное уравнение

L

J [ N 88 0 5 И + M , 88 55 ¹ + 2 Q 88+ N p 88_рр И + M p 88 pp + 2T 88 5 _p + M _p ( ( й, - r 9 ²) 8 u_r + u_z 8 u z + r ² 989 ) +

0                                                                                                      .                                          (5)

+Ju 8u - pr8ur - pz8u J rds -Гr (P8ur + Pz8uz + MИ8u + Pp89)1    = 0, р v v                      z z I [ у r r z z                v p ) 15=0 l где Ns, N3, T, Q, Ms, Mp — внутренние усилия и моменты; Mр, Jр — масса и момент инерции, представляемыми интегралами:

h/2

N i = J c ii d ^ ,   M i = J c^d §

-h/2

h /2

T = J c5p d ^,

- h /2

(i = 5, в), h/2

= J P d ^ ,

- h /2

h /2

Q = J c 5 , (1 - (2 ^ / h )²) d ^ ,

- h /2

h /2

J р = J P^ ² d

- h /2

Подставляя (1) и (2) в (5), получим уравнение мощностей работ относительно вариаций скоростей перемещений 8 u_r , 8 u_z , 8 U _ф , 89 :

J { ( Q V r + N 5 V z ) 8 u r , 5 + ( Q V z - N 5 V r ) 8 u z , 5 + M 5 8 u v , 5 + rT 89 , 5 + ( M р U_z - p_z ) 8 u z +

+ [ r ^-1 N в + M р ( u ; - r 9 ² ) - P r ] 8 u r + ( Q + r ^-1 M _p v z + J р u /) 8 u _ф + r ² M р 989 } rd5 -              (7)

-[ r ( P_r 8 u_r + P_z 8 u_z + M И 8 u _v+ P _p89 ) ] ^ = 0.

Отметим, что при больших деформациях напряженное состояние оболочек стремится к безмоментному, так как изгибные и сдвиговые деформации ограничены рамками применимости теории тонких оболочек и осесимметричной постановкой задачи.

5.    Вариационно-разностный метод решения задачи

Для решения системы уравнений, описывающей динамическое упругопластическое деформирование оболочек при соответствующих граничных и начальных условиях, воспользуемся явной конечно-разностной схемой «крест». Срединную поверхность каждого оболочечного элемента заменим сеточным аналогом с T 1 узлами вдоль меридиана. Кроме этого, введем промежуточную сетку, смещенную на половину шага по отношению к основной. Значения компонент тензоров деформаций и напряжений вычисляются в узлах промежуточной сетки, а перемещения и скорости перемещений — в узлах основной разностной сетки. Определение напряжений и пластических деформаций оболочечного элемента осуществляем в узлах промежуточной сетки на Т ₂ слоях по толщине оболочки. Внутренние усилия и моменты найдем путем численного интегрирования напряжений по толщине.

Пространственные производные и функции аппроксимируем в виде:

f , s = ( f + 1 ^- ft )f ^{A s} _{i +} i/2 , A s_{i +} i/2 = V ⁽ r i + i ^- Г -)^{2 + (} z i + i - z i )² , f + 1/2 = ⁽ f + i ⁺ f V².            (8)

Процесс деформирования во времени разбиваем на временные слои t ⁰, t 1 , ..., t^k , .. с шагом A t^{k +1} = t^{k +1} - t^k . Интегрирование уравнения (7) при дискретизации заменяем суммированием величин виртуальных работ по всем ячейкам сетки, покрывающей оболочку. Собирая коэффициенты при вариациях скоростей перемещений ( 8 i_r ) j , ( 8 i t _z ) j , ( 8 и _ф ) j , ( 80 ) j и учитывая произвольность и независимость вариаций, получаем систему обыкновенных дифференциальных уравнений, описывающую движение дискретной модели оболочки:

( Ф M i r ) j = ( Ф r ) j ,    ( Ф m U _z ) j = ( Ф z ) j ,    ( Ф ji i , ) j = ( Ф_ф ) j ,    ( Ф y 9 ^ = ( Ф д j            (9)

Здесь Ф _r , Ф _z , Ф_ф , Ф₀ — обобщенные силы, действующие на расчетный узел j ; Ф _M , Ф J , Ф Y — узловые масса и моменты инерции.

Коэффициенты уравнений движения (9) определяем в виде:

• -    для внутренних узлов ( Ф_а ) j = ( A _а ) j _{+ 1/2} + ( A ) j _ _1/2 ( а = r , z , ф , 0 , M , J , Y );

• -    для контурных узлов ( Ф а ) _у = ( A а ) _у ± 1/2 + ( A а ) j ( а = r , z , ф , 0 , M , J , Y ).

Здесь A _а представляют собой односторонние вклады обобщенных сил от ячеек, примыкающих к расчетному узлу разностной сетки:

⁽ A r ) _{У ±} 1/2 = ±[ ^{r ( Q} V r ⁺ N s V z ) ] _у ± 1/2 ⁺ 2 ^[A ( ^{r (} Pr ^{+ rM} р ° ² ) ^- N в ⁾ ] . ± _1/2,

⁽ A z ) _{У ±} 1/2 =± ^[ r ^{( Q} V z ^- N s V r ⁾] _у ± 1/2 ⁺ j ^{[ A} srP z ^] j ± 1/2 ’    ⁽ A M ) У ± 1/2 = j [ ^{A SrM} Р ] j ± 1/2 ’

⁽ A ф ) j ± 1/2 =±^[ r^M s ^] _у ± 1/2 ^- 2 ^{[A s} I ^{rQ + M} p V z ⁾] j ± _1/2, ⁽ A ^± 1/2 =±[ r ² T ] _y ± 1/2 , ⁽ A J ) j ± 1/2 = 2 ^{[A srJ} _p] _ ± 1/2 , ( A Y ) j ± 1/2 = 2 [a sr³ M _p] j ± _1/2,    A ; = rP r ,    A> rP_z ,     A ф = rM ^И ,     A e ^: = rP _p ,     A M = A J = A Y = 0.

Решение полученной системы уравнений строим по явной конечно-разностной схеме второго порядка точности. Скорости и перемещения вычисляем по рекуррентным формулам:

^{k +1/2}                               .                                        1

гk +1/2 _ г- -1/2    /x k А-i t              k+ +1 _ k^     k++1/2 к ,k +1     Л/ k +1/2 _ ¹ / * ,k +1    Л/ к\

Jj = f j    ^{+ ( Ф} а ) j ( ф ) k , Jj = Jj ⁺ f j   ^A t  ,   ^A t    = 2^{( A} t   ^+A t )

( f = U r , u_z , u ф , 0 ;    а = r , z , Ф , 0 ; Z= M , J , Y ;    j = 1, T ).

6.    Алгоритм решения задачи

При решении задачи расчетная область разбивается на конические конечные элементы. Узлы сопряжения конечных элементов с толщинами hi+1/2 (s) определяются координатами ri (s), zi (s), i = 0, T1 -1. Задаются начальные, граничные условия и поверхностные нагрузки. Начальный временной шаг At1 выбирается согласно критерию устойчивости разностной схемы [9].

По известному на момент времени t = t^k распределению параметров напряженно-деформированного состояния из уравнения движения при помощи соотношений (10) находятся компоненты скоростей перемещений (г/ r , u z , u t ^ , 9 ) ^k j ^+1/2, перемещений ( u r , u z , u _ф , 9 ) ^k j ⁺¹ и новая геометрия оболочки: m^{k +1} = m “ + f^{k +1}

( m = r , z , p , f = U r , U z , 9 , j = 1, T ).

Следующим этапом расчета на текущем временном слое является вычисление компонент тензора скоростей деформаций по формулам (1), (2) и конечно-разностным соотношениям (8).

При ^ст/стj > ^2/3ст, для нахождения приращений пластических деформаций (Asp)р^^2 организуется итерационный процесс «посадки» девиатора напряжений стj на поверхность текучести (4). Для этого выполняются следующие операции:

• 1.    Вычисляются параметр AX = (1 -^2/3ст,/^стjCTj )Д2(G + qj3)), где СТр=ст‘ + 2GAsp (в первом приближении Asp = 0 стj = стj), приращения пластических деформаций (Asp) = AX ■ стj, приращение параметра Одквиста Ak = ^2/3 ■ ^Asp Asp ; по диаграмме деформирования ст, (к) находится q = [ст. (к^k+Ak) -ст, (к^k)]/Ak ; определяются упругие составляющие приращений деформаций Ase = Ask⁺¹ - (As^p)^k, напряжения ст,_у по формулам (3), шаровая составляющая тензора напряжений

• 2.    Проверяется условие текучести |1 - ^ст /ст j J (^ 2/3ст,) < e = 10^-3, где ст, = ст, (к^k+1). При невыполнении условия текучести осуществляется переход к пункту 1.

• 3.    Находится приращение деформации As_$и изменение толщины элементов оболочки:

  /а_  \ k+1/2         ^Ц/ а _ e  । а _ e \k+1/2   / а _ p . а _ p \k+1/2   /„k+1      тк    Г i .         k++1/2

7.    Регуляризация разностной схемы

ст = ( ст _ss + ст_рр )/3, компоненты девиатора напряжений ст'. = ст _у -ст5 _у .

^{( As}$ ) i + 1/2 = -,      ^{( As} ss ^+As pp ) i + 1/2 - ^{( As} ss ^+As pp ) i + 1/2 , h j + 1/2 = h j + 1/2 |_ 1 ^{+ ( As}" ) i + 1/2 _| ^.

^{1 -Ц}

Далее по формулам численного интегрирования рассчитываются усилия и моменты (6) и формируются коэффициенты уравнений движения для следующего временного слоя, где процесс вычислений повторяется.

Изложенная выше явная разностная схема на гладких решениях имеет второй порядок точности от шагов сетки по пространству и времени

устойчивости схемы получены в [6,9] в

при задании кинематических граничных условий. Оценки (At As,        , виде {At < h]c,, As > h, где h — толщина оболочки,

c

скорость звука. При решении большинства задач достаточная точность достигается при использовании пространственного шага сетки вдоль срединной поверхности порядка толщины оболочки. Но с точки зрения эффективности вне зоны краевых эффектов целесообразно применять сетки с большими размерами ячеек. В этом случае ограничение на временной шаг At < h/c становится весьма обременительным. Поскольку оно определяется длинноволновыми высокочастотными сдвиговыми колебаниями, то целесообразной становится регуляризация разностной схемы, позволяющая понижать частоты этих форм колебаний.

В работах [6, 9] предложен и обоснован метод повышения эффективности явных численных схем интегрирования уравнений теории оболочек типа Тимошенко путем введения регуляризирующего множителя к инерции вращения. В результате при As/h = n >> 1 удается без понижения точности существенно (в n раз) увеличить шаг интегрирования по времени.

8.    Численный эксперимент

Рассмотрим поведение цилиндрической оболочки при монотонном кинематическом нагружении кручением-растяжением [10]. Оболочка имеет геометрические параметры: средний радиус

R 0 = 1,45 - 10^-2м, длину L 0 = 9,2 - IO^-2м, толщину h = 1 - 10^-3 м и изготовлена из стали 12Х18Н10Т с модулем упругости E = 2,1 - 10 5 МПа и коэффициентом Пуассона ц = 0,3 . В качестве диаграммы деформирования ст . ( к ) возьмем экспериментально-расчетную диаграмму, построенную в работе [10]. Один край оболочки ( s = L ₀) жестко защемлен, u r = U_z = й _ф = 0, другой ( s = 0) может перемещаться и / или закручиваться относительно оси с постоянными осевой ( u_z ) и угловой ( А ) скоростями. В расчетах скорости растяжения и кручения примем такими, чтобы скорость деформации составляла 10 с^-1, а начальное распределение скоростей перемещений по длине будем считать линейным. Это обеспечит пренебрежимо малый вклад сил инерции в решение квазистатической задачи.

Для оценки взаимного влияния двух видов нагружения на процесс деформирования введем параметры:

R А                           2 и                  и           R A              ^{h /}2                      h 2

q = "ту,  eI = V ezz + 4/3 epz =    \1 + q ,  ezz = ~T,  ep z = у,  F = 2пR Jстzzd ^,  M = 2пR0 J стрzd §•

V^{3 u} z                             L 0                    L 0            L 0                - h / 2                      - h 2

Здесь: кинематический параметр q характеризует «соотношение кручения и растяжения» (при чистом кручении q = го , при одноосном растяжении q = 0, при комбинированном нагружении 0 <  q < го ); б , , б zz , Б р _z — условные интенсивность деформации, осевая и сдвиговая деформации соответственно; u_z и А — осевое перемещение и угол закручивания между краями; F — осевая сила; M — крутящий момент. Компоненты ст _zz и ст_{р z} определяются преобразованием компонент тензора напряжений Коши из местного базиса O ’ s ^ в общий O rz . В предположении q = const общую работу осевой силы и крутящего момента можно выразить через обобщенную силу W : A = J Fdu_z + J Md А = J Wd б I . 000

В качестве критерия потери устойчивости процесса однородного пластического деформирования длинной оболочки с локализацией деформаций в виде шейки принимается условие dW/d б I = 0, характеризующее момент достижения обобщенной силой W максимальных значений. Данное условие является обобщением известного условия А. Консидера dF/d б I = 0, полученного при растяжении стрежней [11].

На рисунке 1 приведены зависимости от условной осевой деформации б zz и условной интенсивности деформаций б , следующих безразмерных силовых параметров: осевой силы F* = F^ F T , где F T = 2 п Rh ст T , ст _т =ст * ( к = 0 ) ; крутящего момента M* = MM T , где M T = 2 п hR 2 CT T] V3 ; обобщенной силы W* = WW T , где W T = L ₀ F T , при пяти значениях параметра q = 0; 0,5;1; 4; 8. Точками на кривых отмечены моменты достижения обобщенной силой W максимальных значений, после прохождения через которые наблюдается потеря устойчивости оболочки. Резкое изменение интегральных силовых характеристик после потери устойчивости объясняется тем, что условная интенсивность деформаций б I не учитывает локального изменения геометрических параметров оболочки. Рост осевой силы F * в зависимости от параметра Одквиста к в шейке происходит плавно и после момента потери устойчивости.

На рисунке 2 показаны распределения относительного изменения радиуса u_r R ₀ вдоль оси оболочки z/L ₀ при q = 0,1, 4, 8 (пунктирными линиями отмечены формы в моменты потери устойчивости оболочек, штрихпунктирными — формы оболочек при дальнейшем нагружении). Здесь же для сравнения приводятся формы оболочек при чистом растяжении ( q = 0) в моменты времени, соответствующие моментам потери устойчивости оболочек при q = 1, 4, 8 (сплошные линии). До момента потери устойчивости форма оболочки определяется только ее относительным удлинением б _zz и не зависит от доли кручения.

При одноосном растяжении потеря устойчивости происходит при б zz = 0,5. Увеличение доли кручения вызывает потерю устойчивости на более ранней стадии растяжения, при этом условная интенсивность деформации возрастает, что видно из рисунка 3, на котором по оси абсцисс отложен параметр q , по оси ординат — б zz и б , в момент потери устойчивости.

Сравнение результатов расчета и эксперимента [10] по остаточной форме при растяжении ( q = 0, б , = 0,56) показало, что различие составляет 2,5% как в изменении диаметра, так и толщины оболочки в шейке.

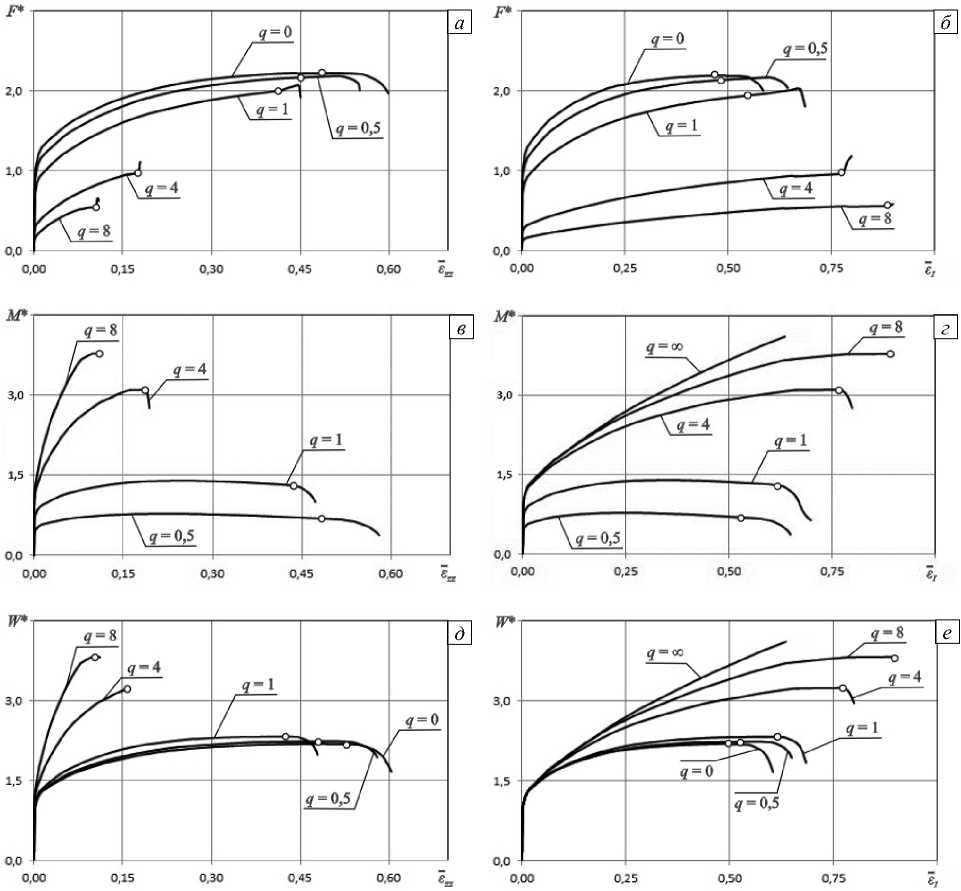
Рис. 1. Зависимости от условной осевой деформации ( а , в , д ) и условной интенсивности деформаций ( б , г , е ) безразмерных силовых параметров: осевой силы ( а , б ); крутящего момента ( в , г ); обобщенной силы ( д , е )

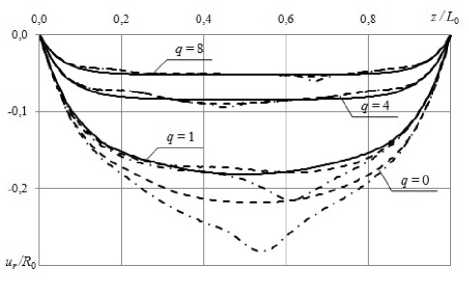
Рис. 2. Относительное изменение радиуса по оси оболочки в зависимости от параметра q

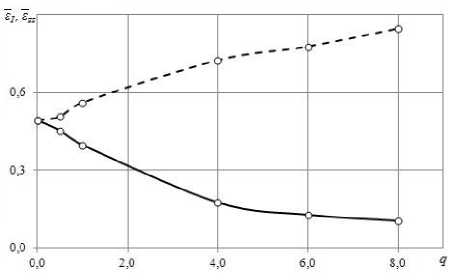
Рис. 3. Зависимость условной осевой деформации (сплошная линия) и условной интенсивности деформаций (пунктирная линия) от q

9.    Заключение

Разработанная методика и программа позволяют проводить численное моделирование осесимметричных упругопластических процессов деформирования и предельных состояний оболочек вращения в широком диапазоне скоростей нагружения (от квазистатических до динамических). За базовую взята вариационно-разностная методика решения осесимметричных задач при больших деформациях оболочек вращения путем пошаговой перестройки геометрии оболочки. Вращение элементов как жесткого целого при кручении учитывается введением коротационной производной Яуманна при умеренных сдвиговых деформациях.

Методика проста в численной реализации и предоставляет возможность рассчитывать оболочки с любым очертанием меридиана. Приведенный выше пример решения задачи с образованием шейки при растяжении с кручением цилиндрической оболочки демонстрирует работоспособность методики и эффективность при больших деформациях.

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках реализации ФЦП «Научные и научно-педагогические кадры инновационной России» на 2009-2013 гг. (соглашение 14.132.21.1812), Совета по грантам Президента РФ для ведущих научных школ (грант НШ-2843.2012.8), а также при финансовой поддержке РФФИ (проекты № 11-08-00565а, 12-08-31190-мол_а, 12-08-33106-мол_а_вед, 12-08-12044-офи_м).