Численное решение обыкновенных дифференциальных уравнений второго порядка с переменными коэффициентами методом конечных разностей с разностными схемами четвертого порядка точности

Рассмотрим краевую задачу:

f1(x)y"(x) + f2(x)y'(x) + f3(x)y(x) = f4(x)    (1).

На отрезке x G [а, Ь].

С граничными условиями вида

Г у(а) = Л

(у(Ь) = В

Будем считать, что функции у(х), / 1 (х), / 2 (х), / 3 (х) и /₄(х) определены и непрерывны на [ct, h], их значения и аргумент принадлежат области действительных чисел, а краевая задача поставлена корректно, то есть:

• 1)    Решение задачи существует.

• 2)    Решение задачи единственное.

• 3)    Решение задачи непрерывно зависит от входных данных.

Для численного решения задачи разобьем отрезок [c, h] на сетку, состоящую из N + 1 одинаковых узлов, тогда координата узла сетки задается соотношением х = c + nh

Где п = 0, N — индекс узла сетки, h = —- — шаг сетки. N

То есть выберем равномерную сетку, к которой узлы расположены друг от друга на равном расстоянии. Численное решение задачи сводится к отысканию приближенного значения функции у(х) в узлах этой сетки.

Запишем разностные схемы для аппроксимации производных:

„^ ₌ -У⁽х — 2h) + 16у⁽х -h) — 30у⁽х) + 16у⁽х + h) — у(х + 2h) _। 4^

у⁽х — 2h) — 8у⁽х — h) + 8у⁽х + h) — у(х + 2h)

У (х) =----------------------7777----------------------+ 0⁽h⁴⁾

Где член 0(h4) характеризует четвёртый порядок точности аппроксимации производных.

За исключением некоторых оговорок, которые в данной статье не будут рассмотрены, чем выше порядок точности, тем ближе наше решение окажется к действительности.

Обычно в подобных статьях рассматривают второй порядок точности аппроксимации производных, мы же воспользуемся разностными схемами более высокого порядка.

Следует также отметить, что обычно переменный коэффициент при старшей производной опускают, считая, что на него можно разделить. Но мы делать этого не будем, так как по мнению автора в некоторых случаях намного удобнее записать уравнение в виде (1).

Более того, если положить этот коэффициент равным нулю, получим дифференциальное уравнение первого порядка. Это делает наш инструмент еще более универсальным.

Подставим разностные схемы в исходное уравнение:

—у(х — 2h) + 16у(х — h) — 30у(х) + 16у(х + h) — у(х + 2h) f(х) ------------------------ Л------^---------^-----

+

+f 2 ⁽X⁾

у(х — 2h) — 8у(х — h) + 8у(х + h) — у(х + 2h)

+

12h

+fз(x)у(x) ~ Ь(х)

Умножим все слагаемые на 12h² и приведем подобные. В итоге получим выражение:

у(х — 2h)(hf2(x) — fi(x)) +

+у(х — h)(16fi(x) — 8hf^(x)) +

у(x)(12h2fз(x) — 30f1(x)) +

+у(х + h)(16fi(x) + 8hf2(x)) +

+у(х + 2h)(—hf2(x) — fi(x)) « 12h2f4(x)  (2).

Положим k1 (%) ЕЕ (//2 (%) — AGO), k2 (%) = (16/1 (%) - 8hf2 (%)), кз(х) = (12^2/з(%) - 30/1 (%)), k4(%) = (16f1(%) + 8hf2(%)), k5(%) = (—hf2(%) — f1(%)),

/(%) = 12^ 2 / 4 (%).

Суть метода конечных разностей состоит в том, что выражение (2) справедливо на всем отрезке [а, b], следовательно, мы можем составить систему из W — 4 уравнений, следующего вида:

у(a)k₁(a + 2h) + у(а + h)k₂(a + 2h) + у(а + 2h')k₃(a + 2h) +

+у(а + 3h)k 4 (a + 2h) + у(а + 4h)k₅(a + 2h) = /(а + 2h) —

Первое уравнение системы.

Поясним, что взять % < а + 2h мы не можем, так как тогда первое слагаемое окажется за пределами исследуемой области.

у(а + h)k1(а + 3h) + у(а + 2h)k2(a + 3h) + у(а + 3h)k3(a + 3h) +

+у(а + 4h)k4(a + 3h) + у(а + 5h)k5(a + 3h) = /(а + 3h) —

Второе уравнение системы.

у(Ь — 4h)k₁(b — 2h) + у(Ь — 3h)k₂(b — 2h) + у(Ь — 2h)k₃(b — 2h) +

+у(Ь — h)k₄(b — 2h) + у(b)k₅(b — 2h) = f(b — 2h) —

N — 4-е. уравнение системы.

По той же причине мы не можем взять % > b — 2h.

Итак, имеем N — 4 уравнений системы. Чтобы система была разрешимой, необходимо составить еще четыре уравнения.

Два из них возьмем из граничных условий:

у(я) = Л, —  N — 3-е. уравнение системы.

у(Ь) = В,—  N — 2-е. уравнение системы.

Оставшиеся уравнения будем искать, составив выражение с использованием разностных схем второго порядка точности:

уЧх ^^-^ — ^ + ОМ.

2ft

У--(х)

у(х + ft) — 2у(х) + у(х — ft) ft²

+ 0(ft2).

Опуская арифметические преобразования, получим схожее с (2) выражение:

у(х — ft)(2/1(x) — ft/^x)) + y(x)(2ft2/з(x) — 4/1 (х)) + +у(х + ft)(2/1(x) + ft/2 (х)) ~ 2ft2/4(x)

Свяжем этим соотношением точки на границе области: у(а)(2/1 (а + ft) — ft/^a + ft)) + у(а + ft)(2ft2/3(a + ft) — 4/1(61 + ft)) +

+у(а + 2ft)(2/1(a + ft) + ft/2(a + ft)) ~ 2ft2/4(а + ft) —

N — 1-е. уравнение системы.

у(Ь — 2ft)(2fi(b — ft) — ft/,(b — ft)) +

у(Ь — ft)(2ft2/3(b — ft) — 4/1 (b — ft)) +

+у(Ь)(2/1(Ь — ft) + ft/2(b — ft)) ® 2ft2/4(b — ft) —

N-е. уравнение системы.

Таким образом, мы заполнили систему N-уравнений. Она всегда имеет нетривиальное решение, если все ее уравнения являются линейно независимыми. Более того, это решение будет единственным вследствие линейности компонентов, входящих в уравнение (1).

Решая численно данную систему уравнений любым доступным методом, например, методом Гаусса с выбором ведущего элемента по строке, можно получить приближенные значения функции у(х) в узлах сетки.

Проиллюстрируем возможности метода на примерах:

• 1)    Рассмотрим краевую задачу

у" СО + уСО = 0.

У(0) = 0,

у(30) = sin(30).

Ее аналитическое решение имеет простой вид у(х) = sin(x).

Решим задачу численно вышеизложенным методом. Для этих целей была специально написана прикладная программа. Внешний вид которой представлен на рисунке 1.

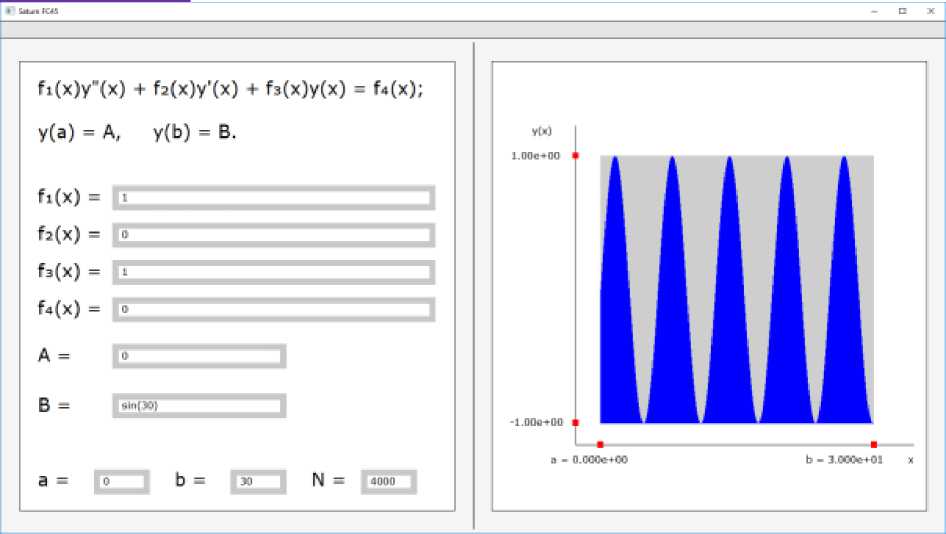
Рисунок 1. Внешний вид программы.

На современном компьютере для N = 4000 узлов сетки весь алгоритм выполняется менее секунды.

Пользователю предоставляется эскиз полученного результата, а также все полученные значения сохраняются в отдельный файл для более детального анализа.

Как видно из графика 1, численное решение этой задачи очень хорошо ложится на аналитическое, что свидетельствует о корректной работе алгоритма.

Для этой задачи максимальная ошибка численного решения составила

max(|sin(x) — у(х)|) « 6,8 * 10-10

Что весьма неплохо в связи с наличием численной ошибки при вычислении чисел с плавающей точкой на ЭВМ.

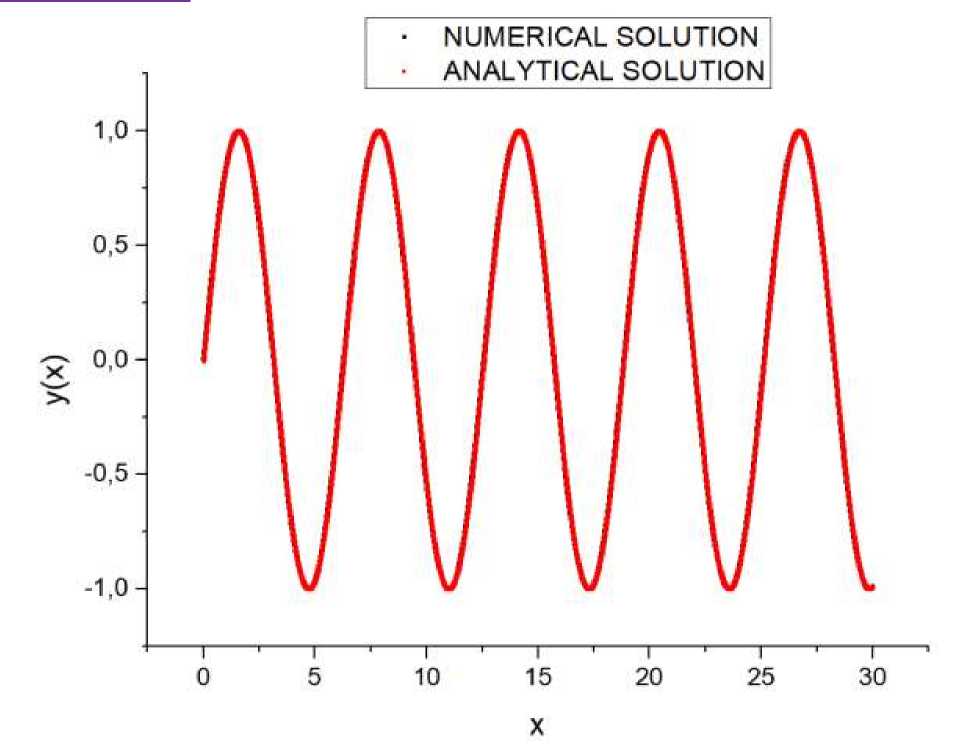
График 1. Аналитическое и численное решения задачи.

• 2)    Попробуем решить более сложную задачу

у"(х) + ^/(x) + у(х) = 0.

X

у(0,01)=/о(0,01), у(15)=/о(15).

Где /0(х) — функция Бесселя нулевого порядка.

Именно ее мы и ожидаем получить в качестве решения.

Как и в предыдущем примере численное решение хорошо ложится на аналитическое (см. график 2).

А максимальная ошибка составила

max|/0(х) — у(х)| « 0,01.

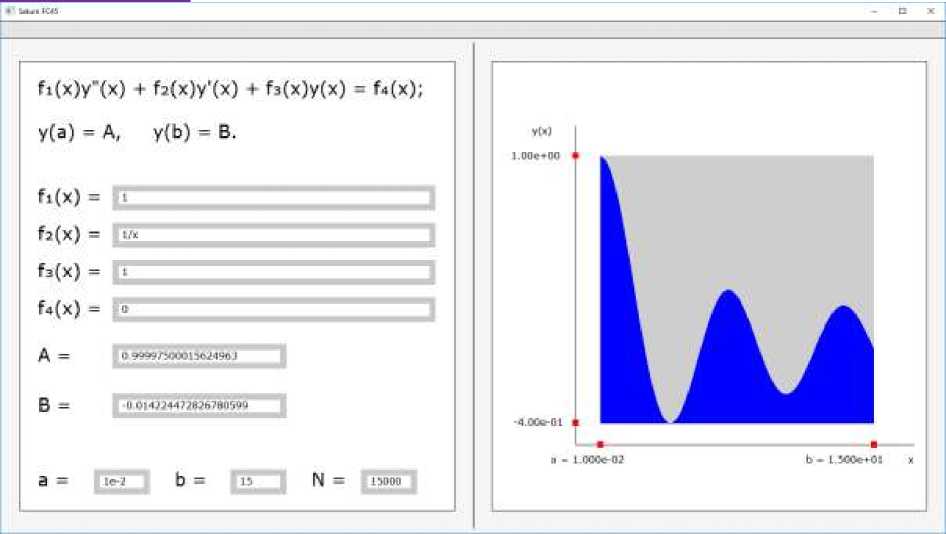
Рисунок 2. Значения, использованные для решения задачи.

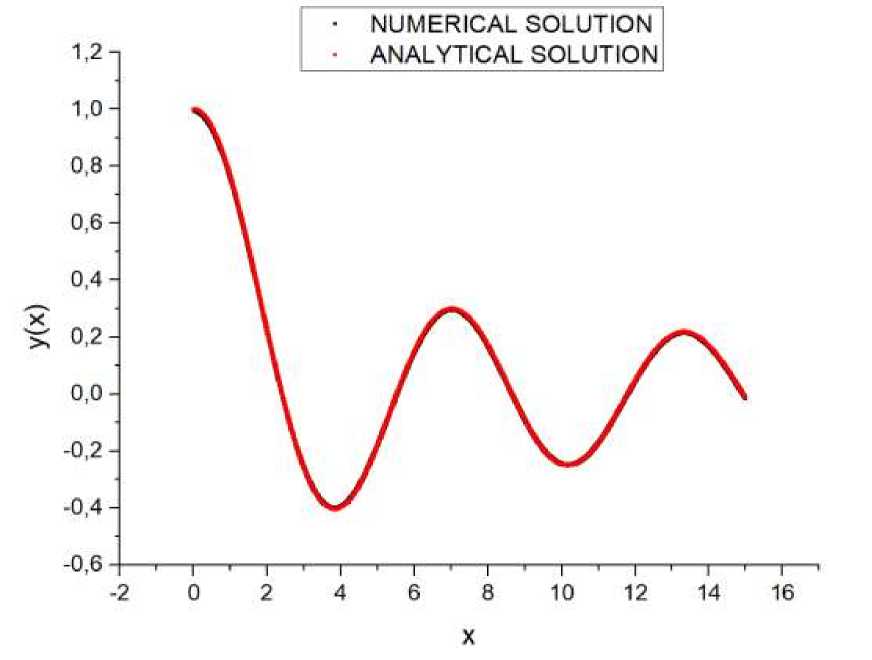
График 2. Аналитическое и численное решение уравнения Бесселя.

Таким образом, мы получили достаточно универсальный инструмент решения краевых задач с обыкновенными дифференциальными уравнениями второго порядка, который может быть использован для научной деятельности в соответствующих областях.

Стоит отметить и некоторые недостатки метода конечных разностей:

• 1)    Данный метод требователен к памяти, так как по сути мы заполняем двумерный массив N*N элементов, который из расчета 8 байт на элемент при N=15000 занимает около 1,68 Гбайт.

• 2)    Сложность адаптации метода для многомерных задач:

очень легко запутаться в элементах системы, затрачиваемая память растет нелинейно, вычислительных ресурсов обычного компьютера недостаточно.

Поэтому для решение краевых задач с дифференциальными уравнениями в частных производных следует обратиться к другим методам.

Что же касается обыкновенных дифференциальных уравнений, метод конечных разностей показал неплохие результаты и алгоритм решения краевых задач на его основе вполне справляется с возложенной на него задачей.