Численное решение одномерной плоской задачи Стефана

При указанных допущениях математическая модель задачи в безразмерных переменных и величинах включает в себя уравнения распространения тепла для каждой из зон:

д© А а2©

с— = л—г, дт     ду2

где C = ^	1, c 2 ρ 2, 1 c l Р 1	при	У <  У ф	л = -	1’ λ 2 [ ^ 1 ’	при	У <  Уф	т © =	- T 1
		при	У >  У ф ,			при	У >  Уф ,	T 2	- T, '

z

у=т, h

z ф tλ

УФ = V, Т = /     ■ h       h2с1ρ1

Здесь z – пространственная координата; t – время; h - продольный размер физической области; T - температура в точке с координатой z в момент времени t ; T ₁ , T ₂ - масштабные значения температуры, первое из которых соответствует ее значению при z=0 , а второе – при z=h ; c , λ , ρ -соответственно удельная теплоемкость, коэффициент теплопроводности и плотность вещества; индекс ф относится к величинам на границе раздела между зонами; 1 – к левой зоне, 2 – к правой; z_ф - координата фронта фазового превращения.

Кроме того, модель включает граничные условия первого рода:

при у = 0 : © = 0 ,                                   (2)

при у = 1 : © = 1 ,                                     (3)

что соответствует тому, что на одной из границ на протяжении всего периода наблюдения поддерживается температура T ₁ , а на другой – T ₂ .

Начальное распределение температуры полагается однородным:

при т = 0 , у е (0;1] : 0 = 1 .

Дополнительно на “межфазной” границе требуется выполнение условий непрерывности температуры и теплового баланса, то есть при т >  0 , у = у ф :

^{0 (} У ф ^{- 0)} = ^{0 (} У ф + ⁰⁾ = ⁰ ф ;

—

5 у

^У Уф ^{- 0}

Л—

5у   п z уф+0

= q • V ,

dyф где V =     , dτ

0 Ф =

Т

Tф

- T 1

т

T 2

- T

q = —:— ^ф —।,   T, - температура фазового перехода;

c T - T    ^ф

q_ф - теплота фазового перехода в расчете на единицу массы вещества в состоянии 1; V - безразмерная скорость перемещения фронта фазового превращения.

Заметим, что задача (1) – (6) соответствует процессу фазового превращения вещества, первоначально находившегося в однородном состоянии с температурой Т2, когда на левой гра нице, начиная с начального момента времени и в дальнейшем, устанавливается температура T1• Подразумевается, что T0 < Тф < T1•

Из (4) в силу очевидного неравенства 0 < 0 _Ф <  1 следует, что начальная координата фронта у ф (0) = 0 .

Для расчета начальной стадии процесса, а также для тестирования численного алгоритма применим аналитическое решение задачи для полубесконечного пространства.

Для малых значений переменной времени τ влияние правого граничного условия (3) несущественно для развития процесса. Поэтому заменим его условием на бесконечном расстоянии:

при у = да : 0 = 1 .                                       (7)

Будем искать решение задачи (1),(2),(4)-(7)

в виде 0 ( т ; у ) = f ( п ) , где п = "^ • τ

Уравнение (1) удовлетворяет функция:

п

Ь 1 J exp

Г .2 7

—

f ⁽п ) = -

η h1 J exp

k

V

Г —

u

— du + b ,

4           2’

при 0 <  п <  к

V

Cu ² L , , ---- du + h , 4Л ²

при к <  п < ^да ,

где п_ф = к , соответственно, у ф = к Т ; V =

k

. Чтобы выполнялись граничные условия и ус-

ловия на границе раздела “фаз” (при п_ф = к ), константы в (8) должны определяться из следующих выражений:

b 2 = 0 , b1 = 1-----

Л ^exP

^{1 +} 2 Л J ^exP

С ( к ² - u ²)L

--------^L I du

4 Л

Г к ² ) f ^-tI J ^exp

V ⁴ 7 к

С ( k ² - u ²⁾

V

4 Л

k

I du + J exp

,

Г u ² L

-т Idu

V ⁴ 7

,        1

h i =л exp

Г Ck2)

4Л

V 7

г

• exp

V

( К2 Л

-Т 6

V 4 7

kq

k h2 = bi J

exp

V

2 u

⁴ 7

du .

Как видно, приведенные соотношения зависят от безразмерной координаты границы раздела П ф = k . Последняя, в свою очередь, определяется из трансцендентного уравнения:

h i = ® ф . (9)

В качестве модельных примем следующие значения входящих в задачу констант: Л , = 1,65 Вт, ( м • К ) ; Л 1 = 1,32 Вт/ ( м • К ) ; c ₂ = 1220 Дж/ ( кг • К ) ; c 1 =1640 Дж/ ( кг • К ) ; р ₂ =1780 кг/м ³ ; р 1 =1800 кг/м ³ ; д_ф =66740 Дж/кг ; h =10 м ; 7 } =+6°С; Т 2 = -2°С; Т_ф =0°С.

Решением уравнения (9) для базового набора параметров является k = 0,5003 . Соответственно, зависимость от времени координаты фронта фазового превращения в задаче с полубес-конечным физическим пространством определяется безразмерным уравнением:

Уф = 0,5003 лТ . (10)

Для численного решения задачи (1)-(6) с конечными размерами области предварительно перейдем к ее дискретному аналогу. Для этого область решения равномерно разобьем на элементарные контрольные объемы [r—1;r], i = 1,2,...,n, центры которых примем в качестве узловых точек y , и проинтегрируем уравнение (1) по каждому из них [2]. Заметим, что на каждом временном шаге один из контрольных объемов будет содержать поверхность фазового превращения. При интегрировании по контрольному объему, в котором происходит фазовый переход, учитывается условие теплового баланса (6). В результате для расчета температурного поля на каждом шаге по времени получаем неявную систему линейных уравнений относительно температур в узловых точках с трехдиагональной матрицей:

где г = 1,2,...,

a / =1

a0 / k ^{+ 1)} = c о 0 * + ^k 1 ^{+ 1)} + d_t 0 / — ^k 1 ^{+ 1)} + 6 , f 1

n ,   0 (^{k + 1)} = 0 ( УТ + 1 ) ;

r

c / + d / +—

—

r — 1

Ат

, при

с/ = 1

У / + 1

—

Л

I У / + 1

—, при y

i <5

; d / =1

—

—, при y

i >  5

У / ^— У / —1’

Л

I У /

—

, y

при

при

i <  5

;

i >  s

r

c / + d / + C • —

—

r — 1

А т ,

при

‘ < 5 A

; б = 1

i >  5

0 ^{( k} ) • r

^— Г — 1

Ат ’

0 ( ^k ) • C • r

при i <  5

as = cs + ds +

c (rs —.уГ*)±уГ1

Ат

- ^Г5 — 1

;

b =0 ^{( k} ) • ss

;

- r

---° -1, при I >  5

А т

C ( r_s — У фk ^{+ 1)}) + У фk ^{+ 1)}

—

Ат

r

-^{5 — 1} + qV ^{( k} ) ;

у фk ^{+ 1)} = у фk ) + V ⁽ k ) •А т ; у фk ) = У ф ( Т к ) ;

V ^{( k} ) = V ( ^Т к ) ; ^Т к + 1 = ^Т к +^{А т} ; ⁵

-

индекс кон-

трольного объема, в котором происходит фазовое превращение.

Как видно, кроме температур система (11) включает неизвестное значение V(k) скорости фронта фазового превращения. Для решения полученной системы применялся метод сквозной

«прогонки» в сочетании с методом «пристрелки» в отношении величины V ⁽ k ) , что позволяет находить попутно очередную координату поверхности раздела “фаз” у фk ^{+ 1)} .

Результаты проведенных на компьютере численных расчетов для базового набора значений параметров представлены ниже в графическом виде (рис.1). Абсцисса точки излома на каждой из кривых соответствует координате yф фронта фазового перехода, а ордината этой точки равна температуре фазового превращения, которая для базовых величин имеет значение 0ф = 0,75. Последнее из представленных на рис.1 распределений температуры близко к стационарному распределению, когда скорость распространения поверхности раздела “фаз” равна нулю. Для того чтобы рассчитать положение уф7) “стационарного” фронта достаточно в уравнении (1) производные по времени положить равными нулю и воспользоваться условиями теплового балан-0 ф са (5), (6). В результате получаем соотношение уф7) =------------г.

ф 0 ф +Л(1 -0 ф )

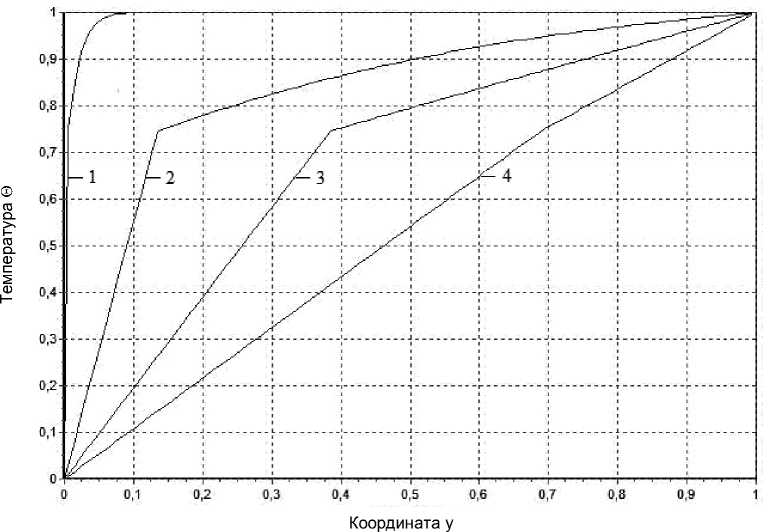
Рис.1. Распределение температуры 0 в различные моменты времени т :

1 - т = 0,0002 ; 2 - т = 0,0777 ; 3 - т = 0,6557 ; 4 - т = 11,71

Для базовых параметров это дает у ф⁷ ) =

— ~ 0706 . Численный расчет, что в некоторой

17    ’ степени иллюстрирует рис.1, действительно приводит к данному значению. Это служит одним из подтверждений того, что разработанный численный алгоритм вполне соответствует описываемому процессу.

На рис.2 представлены зависимости от безразмерного времени τ безразмерных скорости V фронта фазового превращения и координаты самого фронта y_ф , полученные в результате численного решения задачи (1)-(6). Здесь же в виде набора точек показано определяемое из соотношения (10) изменение с течением времени положения границы раздела между зонами для задачи с бесконечной протяженностью физического пространства. Как показывают расчеты, ¹⁹

влияние правого граничного условия в задаче (1)-(6) несущественно, пока фронт фазового перехода y_ф не достигает значений близких к 0,2 (соответственно, пока переменная времени τ не больше 0,16). Об этом свидетельствуют, в частности, почти идентичные распределения температур на каждом шаге по времени в совместной расчетной области для каждой из задач.

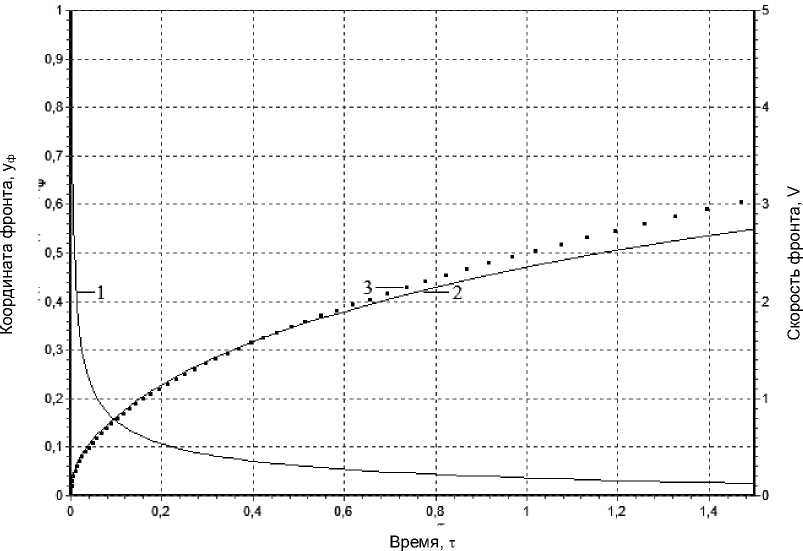
Рис. 2. Изменение поверхности раздела между зонами с различным агрегатным состоянием вещества: 1, 2 – соответственно графики скорости перемещения фронта и координаты фронта;

3 – график изменения с течением времени положения границы раздела “фаз”

Эти распределения определяются по формулам (8). Кроме того, при численном решении задачи (1)-(6) отслеживались изменения величин y_ф τ и 2 V τ , которые в задаче с бесконечной толщиной грунта представляют собой константу k . Оценивать относительную величину разницы между значениями y_ф , полученными для каждой из двух моделей, не имеет смысла, потому что, во-первых, для малых значений времени малы и значения y_ф , и, в силу того, что ЭВМ работает с ограниченным числом разрядов, при малых τ относительная разность может быть довольно большой, а, во-вторых, начальная скорость перемещения фронта в силу модельного представления о разрывности начального распределения температур должна быть бесконечной, чего также невозможно добиться при численном решении с помощью ЭВМ. С учетом указанных обстоятельств, для проверки близости решений разумным представляется соотнесение величин k y = Уф)T и k_V = 2VТ , получаемых в ходе численного решения задачи с конечным продольным размером физического пространства, со значением k , определяемым из (9).

Заключение. Расчеты показывают, что на начальном временном промежутке относительные разницы между k_y и k , а также k_V и k , не превышают 10% от k , причем чем больше τ отличается от нуля, тем меньшей становится эта разница, и лишь тогда, когда начинает существенно сказываться условие на правой границе задачи (1)-(6) (соответствующие τ намного больше зна-²⁰

чения, которое соответствует концу начального промежутка), она приобретает явную тенденцию к возрастанию. Заметим, что при неограниченном возрастании переменной τ кривая 2 (см.рис.2) выходит на горизонтальную асимптоту у = у фс ) (для базовых параметров у = 0,706 ). Последнее означает, что положение фронта стабилизируется. При этом кривая 3 асимптоты не имеет, то есть координата поверхности раздела зон в случае бесконечной расчетной области не имеет верхнего предела.