Численное решение температурных эффектов в полимерных материалах при обработке их импульсными ионными пучками с учетом релаксационного параметра потоков тепла

лицензии, посетите

Современные технологии обработки поверхностей материалов энергетическими источниками различного вида сопровождаются преобразованием энергии в тепловую с целью придания поверхностному слою особых свойств [1].

Обычно этот процесс протекает одновременно с качественным изменением структуры во вновь образовавшемся слое [2–7]. Глубина процесса и толщина слоя могут характеризоваться от мезо- до наноуровня. Несмотря на разнообразие энергетических источников, применяемых в различных областях промышленности, подходы в математическом моделировании этих процессов часто имеют общую основу [8–14]. Особенно это касается процессов, близких к изотермическим, сопровождающихся низкоэнергетическим потоком ионов. При этом математические модели опираются на уравнения неразрывности, движения и баланса массы. В некоторых случаях в уравнении баланса массы необходимо отразить инерционность процессов диффузии, когда конечность времени релаксации становится важной [15–16].

Второй объединяющей чертой в разработке математических моделей является необходимость в описании реальных источников более простыми видами функций [17–19]. В конечном счете описание подобных процессов сводится к хорошо известному классу параболических или гиперболических уравнений. Однако получение решения этих уравнений готовыми и широко распространенными комплексами программ является затруднительным. Причина заключается в существенной разно-масштабности течения диффузионного процесса в пространстве и времени. Временной интервал может измеряться в секундах, а пространственный – на уровне нанометров.

Поэтому целесообразно в данном случае применять конечно-разностные методы с тщательной проверкой точности полученных решений [20–22].

1.    Нелинейная система дифференциальных уравнений

Подробное описание построения уравнения теплопроводности для упругой среды с релаксирующим потоком тепла приведено в статье [23].

В эластомерном материале упругое сопротивление внешней нагрузке происходит за счет изменения энтропии без изменения внутренней энергии. Ограничимся при решении задачи только вопросом изменения температуры тела 0 и будем полагать, что в материале деформации малы и ими можно пренебречь. Это означает, что массовая плотность свободной энергии f должна быть представлена в виде f = cQ0(1 - ln 0) + ^q^q),

Q ^V           2 p c ₀0

а уравнения изменения во времени теплового потока q определяется формулой dq r — = -q - ce grad0. dt

В работе [23] показано, что уравнение теплопроводности в этом случае принимает вид pc fl - Tq -q> 1 d0 = -T dkq -

Q ^   pcQce02 J dt    c00 dt div q + pr ,              (2)

где t - время, p - плотность материала, C q -удельная теплоемкость, т - характерное время релаксации теплового потока, c – коэффициент теплопроводности, r – массовая плотность источников тепла.

В одномерной постановке, когда координатная ось совпадает с направлением движения иона, задача может быть приведена к нелинейной системе дифференциальных уравнений 1-го порядка по времени и пространству:

—

q*  50*  „ q„ д0„ q*

= * c x + * cx —

0*2 J д t *        0* д x *

дq*

cx д--+ (1 - x* )Hhev (1 - x* )Hhev (1 - t* ) д x„ дq * д t*

д0

- q * -     , д x*

которая записана относительно безразмерных величин t *, x ,, 0* ( t* , x* ) и q* ( t* , x* ) , которыми обозначены, соответственно, независимые момент времени и точка на координатной оси, зависимые температура и тепловой поток.

Процедуру обезразмеривания величин t , я , в ( t , x ) и q ( t , x ) в уравнениях (1) и (2) осуществим с помощью релаксационного параметра т , материальных констант р , C q , с_в и характерных параметров ионной обработки ( & 1_0П - время подачи импульсного пучка ионов; e - кинетическая энергия иона; h -максимальная глубина проникновения иона; N - количество ионов, которые во время одного импульса проходят через единицу площади поверхности образца; а - та часть кинетической энергии, которая тратится на разогрев материала и может быть меньше 1, если часть кинетической энергии идет на разрушение полимерных цепей):

. Z1    CrТ Z1         c 6c гТ t = Tt*, x = hx*, v =-----в*, q =------q*,

PCq        PCQh где

2aNe        c p i

Сг=й~к Cx=7pfi-

Список искомых величин в системе (4) для момента времени t перечислим в следующем i + 1 i+i + 1 /п i + 1       i + 1        i + 1        i + 1

порядке: 0 k — 1 , 0 k , 0 k + 1 , q k — 1 , q k , q k + 1 .

Такой порядок позволяет из системы уравнений (4) получить алгебраическую систему уравнений с диагональной матрицей, у которой каждые две строки соответствуют одному моменту времени и могут быть представлены в общем виде:

ав—1 + a^k+1 + a ^k +1 + a 14 qk—1 + a 15 qk + a16 qk+1 = b1

a 2^ ——1 + a 220k+1 + a 2з0k+1 + a24qk—1 + a 25 qk + a26qk+1 = b2 ,

где

^a 11 = c x

q 1

в A x ’

a 12 = ^{1 —} c x

2 q в2 J

At^; a ¹³ =

^— a n^;

Источник тепла управляется функциями Хевисайда H hev ( 1 - x * ) , H hev ( 1 - 1 * ) .

Для решения системы уравнений (3) используем устойчивую конечно-разностную схему [20] с постоянными шагами по времени и координатам h_t и h_x . Для избежания нагромождения вновь образованных индексов у всех безразмерных величин будет опущен индекс в виде звездочки. С учетом этого примечания перепишем систему уравнений (3) в виде конечно-разностных уравнений с постоянными коэффициентами для моментов вре-

a 14 = ^— c x

^a 21 =

мени tj , t_i+l и координатных точек x_k_ ₁ , x_k ,

xk + 1 :

/

—

c

q

/

в

। i + 1

k

—

в

i

k

x

V

в

V

At

= 2 c

q ( ^в

। i + 1

к + 1

—

в

। i +1 Л

’ к — 1

x

в

V

2Ax

+

2 c x

q

к

в 2

—

c

x

a i ^{+ 1} q k + 1

—

i +1 A q k — 1

V

2 A x

+

( 1 — x ) H hev ( 1 — x ) H hev ( 1 — t )

n i + 1 i’      fii + 1     fii + 1

^qk ^{— q}k , ^в к + 1 ^{— в} к —1 _  „

--------+— q ,

At        2 A x

где величинам в и q присваиваются значения, определенные на предыдущем шаге по времени по всей координатной сетке. Для начального шага по времени они определяются из начальных условий.

; ^a 15 = 0; ^a 16 =^{— a} 14 ;

2 A x

2 A x ’

a 22 = ^{0 ;} a 23 =

^— a 21 ;

a ₂₄ = 0;

a 25 =д ^{; a} 26 = ^{0 ;}

b 1 = ¹ — C x

q ²

+ в

( 1 — x ) H hev ( 1 — x ) H hev ( 1 — t ) ;

1 i ^b 2 = ^qk A t

^— q .

Следует заметить, что в таком виде система уравнений (5) не является полной.

Приведем пояснения к этому замечанию. Обозначим количество точек на интервале времени величиной N_t + 1 , на координатной сетке величиной N_х + 1. В этом случае в системе (5) индекс i , привязанный ко времени, может пробегать значения от 1 до N , а индекс k , привязанный к координате, от 2 до N_x .

Отсюда следует, что система (5) состоит из 2 ( N_x — 1 ) уравнений, так как для каждого значения k сформулировано два уравнения. Однако общее количество искомых величин равно 2 ( N x + 1 ) .

Перечислим их:

д i + 1 f+i + 1          i + i + 1 i + i + 1

O1   , o2  ,    , ^Nx , ONx +1 , q i+1, q2+1, ■ , qN, qN+1 ■

Для полноты системы уравнений (5) не хватает четырех уравнений. Дополним ее за счет граничных условий, которые зададим, исходя из следующих соображений. Предположим, что на границах значение теплового потока равно 0, тогда для выполнения второго уравнения системы (3) должно выполняться условие dO ----= 0 ■ dx

Такие граничные условия для крайних точек k =1 и k = N_x + 1 дополнят систему уравнений (5) следующими недостающими четырьмя связями:

o 2 ^{+ 1} - O 1 ^{i + 1} = о ; O N + - O N¹ = 0 ;

q 1   =^0; q N_x + 1 ⁼⁰'

В качестве начальных условий зададим комнатную температуру и нулевой тепловой поток.

2.    Линеаризация системыдифференциальных уравнений (3)

Для избежания трудностей получения решения нелинейной системы уравнений, связанных с необходимостью проверки сходимости численной схемы на достаточно длительных интервалах времени, рассмотрены условия, позволяющие осуществить линеаризацию нелинейной системы. В данной работе применена процедура линеаризации нелинейной системы при малых значениях параметра релаксации.

Рассмотрим процессы (1, 2), при которых характерное время релаксации т имеет настолько малое значение, что выполняются следующие неравенства:

т                 т      d ( q • q )

--------- << q • q ,

PCqCoO2   " " CoOdt

В этом случае система уравнений (3) может быть приведена к линейному виду:

-cx ^ + (1 - x* )Hhev (1 - x* )Hhev (1 - t* ) > dt*d dq*dO

---= — q * —----■ dt*dx*

Описание процедуры построения конечно-разностных уравнений для этой системы будет опущено, так как оно идентично с приведенным в предыдущем параграфе. При этом воспользуемся аналогичной оговоркой, а именно: для того чтобы исключить нагромождение вновь образованных индексов, у всех безраз- мерных величин опустим индекс в виде звездочки. Приведем систему уравнений (7) к виду, аналогичному системе (5), получим следующий список коэффициентов:

a i = о; a 12 =     ; а з = о;

¹¹                A t ¹³

a 14 = ^- cx\ —; « 15 = о; « 16 =- « 14 ;

2 Ax a 21 =

—

7 .   ^; a 22 = ^{0 ;} « 23 = ^- « 21 ^; a 24 = ^{0 ;}

2 Ax a25 =д ; a26 = 0 ;

b 1 =

L O k + ( 1 - x ) H hev ( 1 - x ) H hev ( 1 - t ) ; A t

1 i ^b 2 = -^k A t

^- q ■

Очевидно, что коэффициенты a2j и свободный член b после линеаризации остались неизменными.

• 3.    Применение конечно-разностных схем к формированию профилей тепловых потоков в полиуретане, поверхность которого подвергается одним импульсом ионов азота

  Конечно-разностную схему (5), соответствующую системам уравнений (3) и (7), применим для моделирования профилей тепловых потоков, возникающих на поверхности полиуретанового материала, обрабатываемого ионами азота с энергией e =20 кэВ до флюенса 10¹⁶ ион/см², достигнутого за 200000 импульсов с частотой 100 Гц. В данном случае следует отметить, что в реальных процессах имеет место неоднородность концентрации распределения ионов в потоке. Поэтому рассматривался участок материала, в котором количество ионов азота N , проходящих во время одного импульса через единицу площади поверхности, превышает задаваемое в эксперименте значение в 5 раз. Глубина проникновения ионов равнялась 80 нм. Длительность импульса &1_0П задавалась равной 20 микросекунд.

• 3.1.    Проверка точности вычислительной схемы

Эти данные соответствуют значениям величин в проводимых в ИМСС УрО РАН экспериментах. Объемная плотность полиуретана, его удельные теплоемкость и теплопроводность имели значения р=1200кг^м-3, Cq=1380 м^с-^К-1, c =028 кг∙м∙с-3∙К-1. и

По имеющимся в литературе данным релаксационный параметр т меняется в очень широком диапазоне от пикосекунд [24] до нескольких секунд [25, 26]. Предпримем попытку определить, какие значения т можно считать малыми в рамках поставленной задачи. Для начальных расчетов примем значение т равное 0.0001 секунде, рассчитанное теоретически и приведенное в работе [27] для наножидкостей. Так же оценим, как изменятся результаты расчетов при т = 0.001 и 0.01 с.

Для проверки точности схемы (5) проводились вычисления на вдвое сгущающейся сетке при начальном шаге h =0.01 и постоян- ном шаге h =0.01 на интервале времени t = [0; At]. Вычисления на сетках с шагами hx, hx /2 и hx /4 показали сходимость результатов, выраженных в уменьшении значений величин Z и Zq (табл. 1, 2):

Z в

= max

Z_q = max

|^Ав h x ^(A t , x )    ^A) h x /2 ^(A t , x )|

A9 h x ( A t , x )

|^A q h _x ^(a t , x ^)-A q h _x /2 ^(a t , x )

^A q h _x ^(a t , x )

.

Величина A0 _h ( A t, x ) равна разности полученных решений систем (4) и (7) на сетке h .

Таблица 1

Сходимость результатов для нелинейной системы (3)
т =0.0001 c
hx	Z e	Z q
0.010	0.00986952	0.010007657
0.005	0.00488403	0.004965185
т =0.001 c
0.010	0.00992625	0.005155702
0.005	0.00493693	0.002564946
т =0.01 c
0.010	0.00620040	1.30749∙10-5
0.005	0.00304604	4.13950∙10-6

Таблица 2

Сходимость результатов для линеализированной системы (7)
т =0.0001 c
hx	Z e	Z q
0.010	0.010108938	0.009993954
0.005	0.005002969	0.004951791
т =0.001 c
0.010	0.009811711	0.005332388
0.005	0.004873712	0.002565516
т =0.01 c
0.010	0.006184282	4.54843∙10-7
0.005	0.003038161	0.00000000

Данные в таблицах подтверждают стабильное уменьшение значений величин Z и Z_q при сгущении сетки, поэтому дальнейшее численное моделирование проводилось при h =0.01 и h =0.01.

4.    Обсуждение результатов

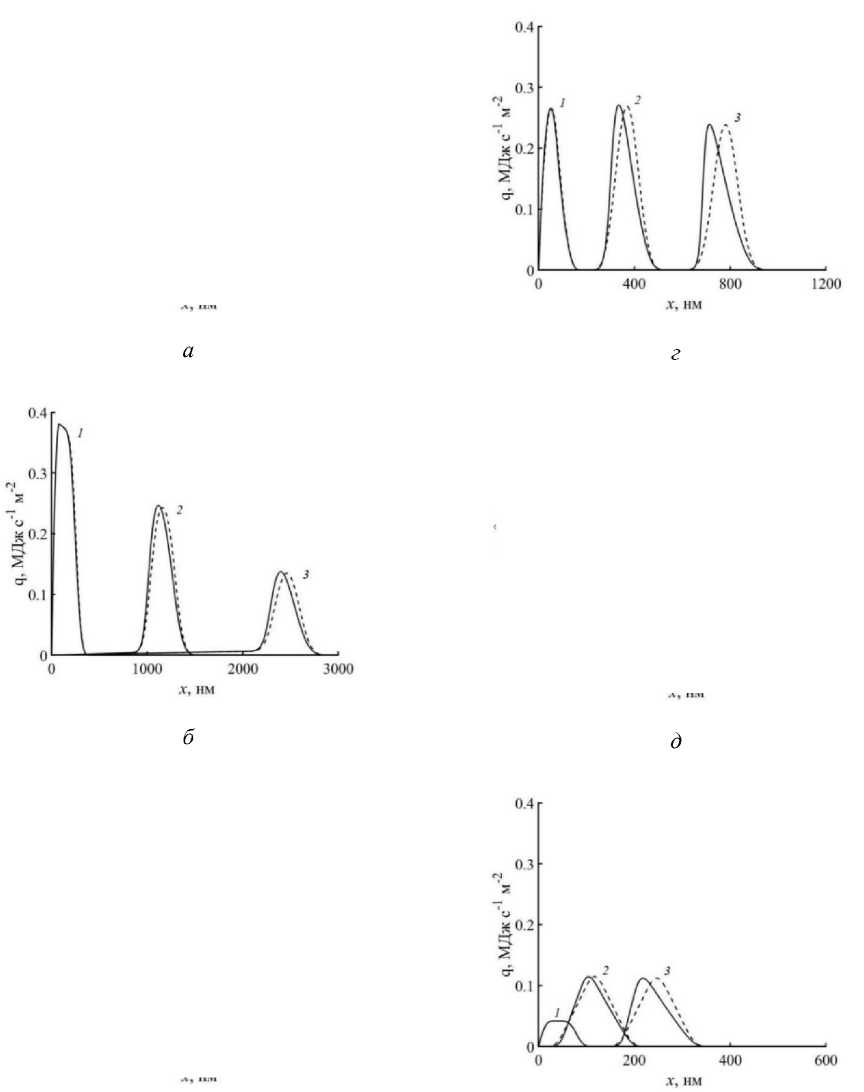
Полученные системы уравнений (3) и (7), сведенные к виду (5), решались методом матричной прогонки (рис. 1). Расчеты проводились для трех разных значений параметра т , последовательно равных 0.0001, 0.001 и 0.01 секундах, с целью получения оценки влияния этого параметра на температурно-волновые процессы, проходящие вблизи к обрабатываемой поверхности материала.

Следует заметить, что построенные температурные и тепловые профили в материале представляют собой движущуюся волну от поверхности в глубину материала с отрывом в момент времени прекращения действия импульса. Несмотря на появление тепловой волны, передача тепла всегда происходит от границы материала в глубь образца, и с течением времени волна уходит дальше в глубину материала.

С другой стороны, на рисунках хорошо видно, что увеличение значения величины т приводит к повышению температуры на обрабатываемой поверхности материала. При этом изменение температурных профилей сопровождается ярко выраженным уменьшением длины волны.

Чем больше значение параметра релаксации, тем медленнее идет движение тепловой волны в глубину материала.

в

е

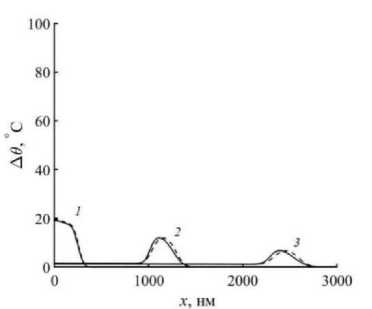
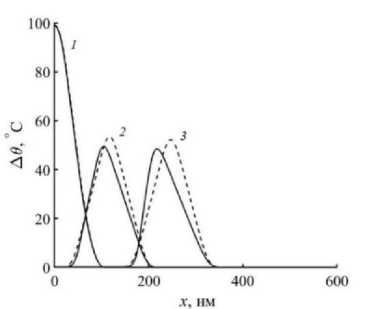
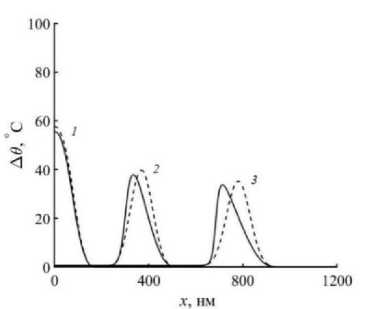
Рис. 1. Профили изменения температуры (а, в, д) и теплового потока (б, г, е) для моментов времени №[ _оп (линии 1), 5^t [ _on (линии 2), 10At [ _on (линии 3). Решение нелинейных уравнений (3) показано сплошными линиями, линеализированной (7) – пунктирными линиями. τ =0.0001 с (а, б); τ =0.001 с (в, г); τ =0.01 с (д, е)

Это означает, чем больше τ , тем ощутимее колебательные температурно-волновые процессы возникают вблизи к поверхности материала, которые, вероятно, способны повлечь за собой возникновение более высокого напряженно-деформированного состояния в этом слое. При сравнении результатов решений нелинейной (3) и линеализированной (7) систем дифференциальных уравнений визуально обнаружилось расхождение температуры и теплового потока.

Для оценки расхождения введем величину S , представляющую собой относительную погрешность вычислений приращения температуры:

_s ^M^x-^tx _100%

• ⁹ Mf ( t , x ) ^, (8) где A9_F ( t, x ) и A9_L ( t, x ) - максимальные значения повышения температуры во всем материале в момент времени t , полученные, соответственно, с помощью систем уравнений (3) и (7). Изменение значений погрешностей S и S q для разных т приведены на рис. 2. Величиной 8 q оценивается погрешность вычисления теплового потока, определяемая по аналогии с формулой (8).

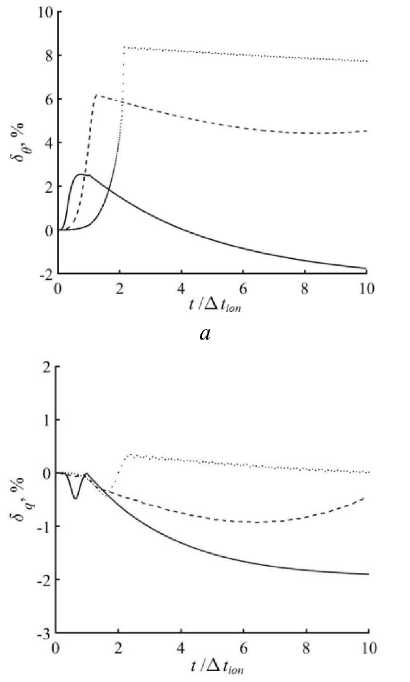
б

Рис. 2. Относительные погрешности вычислений температуры и потока S ₉ (а) и 5 q (б). т =0.0001 с (сплошные линии); т =0.001 с (пунктирные линии); т =0.01 с (точечные линии)

Анализируя значения погрешностей S и S q , можно оценить правомерность линеаризации системы уравнений (3), следующее из определения значений величины т , при которых незначительно искажается решение нелинейной системы уравнений (рис. 2).

Однозначно можно отметить следующее. Линеаризация системы (3) и увеличение т в пределах расчетного интервала времени t = [0; 10 At _ioJ слабо сказываются на значениях теплового потока q , на значениях же температуры 9 - довольно существенно.

На рис. 2а показано, что при т =0.01 секунд погрешность S_e продолжает расти даже после выключения потока ионов и к моменту времени t > 2 At _ion достигает значения более 8%. Очевидно, что при таком значении т не следует пользоваться решением линеализиро-ванной системы.

В дополнение к этому, следует обратить внимание на значительное расхождение пиков волн на координатной сетке при сравнении решений нелинейной и линеализированной систем (рис. 1).

Исследование причины появления этого расхождения в рамках данной работы не проводилось, поскольку главная цель заключалась в демонстрации зависимости рассматриваемых явлений от параметра релаксации, которая выразилась в тенденции роста значения температуры на поверхности и снижения значения теплового потока с ростом значения параметра релаксации.

Выводы

На основе нелинейного уравнения теплопроводности с релаксирующим потоком тепла произведены расчеты изменения температуры и теплового потока в поверхностном слое материала, обрабатываемом импульсным ионным пучком. Численные решения получены с применением метода конечных разностей.

Исследование влияния параметра релаксации показало, что увеличение его значения приводит к повышению температуры на обрабатываемой поверхности материала. При этом изменение температурных профилей сопровождается ярко выраженным уменьшением длины волны. Чем больше значение параметра релаксации, тем медленнее идет движение тепловой волны в глубину материала.

Изложен способ линеаризации уравнения теплопроводности. Проведенный анализ степени различия полученных решений до и после линеаризации уравнения теплопроводности в зависимости от значения параметра релаксации показал, что наиболее ярко расхождение в данных проявляется в несовпадении пиков волн на координатной сетке после выключения импульса. Пики волн, соответствующие нелинейной системе, имеют тенденцию отклоняться в сторону обрабатываемой поверхности.

При увеличении значения параметра релаксации в 100 раз погрешность вычислений температуры после линеаризации растет даже после выключения импульса и превышает 8%. Возможно, что это значение параметра релаксации следует назвать предельным и при дальнейшем его повышении не следует пользоваться решением линеализированной системы уравнений.