Численное решение уравнений Фредгольма с двойной точностью методом вырождения интегрального ядра

© 2025 Пастухов Д. Ф., Пастухов Ю. Ф. Лицензировано по CC BY 4.0. Чтобы ознако- миться с условиями этой лицензии, посетите сайт

Методы решения интегральных уравнений Фредгольма и Вольтерры подробно описаны в работе [1]. Прямые методы [1, стр. 135] и проекционные методы [1, стр. 139]. В работе [2] для решения интегральных уравнений Фредгольма используются сплайны обобщенного вида, интегральное ядро может быть непрерывным, гладким или дважды дифференцируемым на квадрате. Благодаря второму порядку аппроксимации интегрального ядра O ( h ² ) требуется большое число интервалов аппроксимации. В работах [3, 4] предложен метод подбора подобластей на базе полиномов Канторовича для решения уравнения Фредгольма второго рода, а также рассматривается специальный вариант метода коллокации на базе полиномов Бернштейна для решения уравнений Фредгольма второго рода, приведены оценки корректности алгоритмов. В работе [5] применен метод коллокации для решения интегрального уравнения Вольтерры второго рода с использованием многочленов Чебышева и Лежандра, произведение интегрального ядра на приближенное решение раскладывается в частичную сумму по системе многочленов Чебышева или многочленов Лежандра. Достигнута минимальная норма Чебышева для невязки задачи 10^-13. В работе

• [6]    решается система интегральных уравнений методом коллокации с узлами многочленов Чебышева первого и второго рода, получены теоретические оценки для корректности алгоритма. В работе [7] предложен метод решении системы нелинейных интегральных уравнений сверточного типа с монотонно выпуклой нелинейностью. В работе [8] предложен обобщенный метод Петрова–Галеркина для решения системы линейных интегральных уравнений Фредгольма второго рода.

В работе [9] методом замены интеграла с квадратурной интегральной формулой с двенадцатым порядком погрешности получено табличное решение линейного интегрального уравнения с двойной точностью. В данной работе, как и в работах [2–8] решение имеет функциональный вид, но использованы более простые координатные степенные функции. Метод получил название модифицированного метода вырождения интегрального ядра для решения линейного интегрального уравнения Фредгольма второго рода . Для достаточно гладкого интегрального ядра по переменной x можно использовать всего двадцать базисных функций и тридцать интервалов интегрирования в квадратурных формулах для достижения двойной точности решения. То есть, во всех примерах норма Чебышева невязки решения равна 10^-15, единственный недостаток алгоритма заключается в явном знании формул для частных производных ядра по переменной x . Алгоритм тестировался на примерах с экспоненциальным изменением интегрального ядра или с периодическим изменением знака ядра. Доказаны 3 теоремы (достаточные условия существования и единственности численного решения задачи (1) алгоритмом (2)–(7)). Полученный алгоритм вместе с известными методами благодаря простоте и высокой точности решения поможет решать интегральные уравнения Фредгольма второго рода с достаточно гладкими интегральными ядрами.

Постановка задачи

Рассмотрим интегральное уравнение Фредгольма второго рода [1, стр.135] b y (x) - A J K (x, s )y (s ) ds = f (x), (x, s ) e [ a, b ] x [ a, b ]. (1) a

В уравнении (1) параметр X, интегральное ядро K ( x , s ) e L ₂ [ a , b ] x [ a , b ] и правая часть - функция f ( x ) заданы. Неизвестная функция должна быть интегрируема с квадратом на отрезке [ a, b ] y ( x ) e L ₂ [ a , b ]. Пусть также частные производные ядра по переменной x непрерывны на квадрате K xi ) ( x , s ) e C [ a , b ] x [ a , b ], i = 0, n .

Известен прямой метод решения интегрального уравнения (1) методом вырожденного ядра [1, стр. 135], который заключается в том, чтобы интегральное ядро разложить в ряд по переменным x, s . То есть, заменить интегральное ядро полиномом двух переменных, как, например, в задаче 29.11 [1, стр. 138]. А затем решить уравнение (1) методом замены ядра. В классическом методе требуется две системы базисных линейно независимых функций { Ai ( x )}= _p { B i ( x )}=j. По одной из систем раскладывается решение, а ядро представляется суммой попарных произведений функций по одной из каждой системы [1, стр. 138]. Чтобы из интегрального ядра K ( x , s ) произвольного вида получить полином по двум переменным необходимо разложить ядро в ряд Тейлора по переменным x, s . В этом идея традиционного подхода решения уравнения (1) методом замены интегрального ядра.

Модифицируем известный метод. В данном случае понадобится одна система линейно-независимых функций {A (x)}L0, x e [a, b]. Будем рассматривать симметричную b—a переменную y| 2 a

b

= x

a

—

a + b     a + b , b — a

—-—, c = —-—, h = —-— относительно середины отрезка

a + ^b г 7 71 ^c = —^-, y ^{e [ —} h , h ^]

и

систему линейно независимых степенных функций

{ ^A i ⁽y ) = y i j n = o ^, y ^e

—

b — a

b — a

,Ё”

.

Идея модифицированного метода вырождения ядра заключается в том, чтобы разложить ядро K ( x , s ) по первой переменной x в центре отрезка c = a +^, x = c + y , dx = dy .

Получаем nini

K (x, s) = K (c + y, s) = Ё KX' \ C, s) y- + O (yn+1) Kn (x, s) = Ё KXi)(c, s) y-.(2)

i=0                 i!                                    j=0

В формуле (2) обозначим K xi ) ( c , s ) = q i ( s ), i = 0, n , s e [ a , b ]. Разложим решение y ( x ) на отрезке [ a ,b ] в сумму

n

y ⁽ x ) = f ⁽ x ) + ² Ё A ⁽ y ) ^D i •

i = 0

В формуле (3) D i , i = 0, n - называется

вектором коэффициентов разложения ре-

шения по базисным функциям { A i ( y ) = y i |₌₀.

Подставим разложения (2), (3) в уравнение Фредгольма второго рода (1).

b

y ( x ) — 2 J K ( x , s ) y ( s ) ds = f ( x ), A i ( y ) = y i e

a

n

b

n

i

nn

f ⁽ x ) + ² Ё y i ^{D — 2} Ё q i ^{( s} ) y r i = 0              ^Jai = 0          i ^! L

^

f (s)+2Ё Aj(s—c) jDj ds = f (x) ° j=0                J

n             ^b n            i

Ё y ' ^D i ^— (Ё q i ⁽ s )7

i = 0             _a i = 0           i^!

f ( s ) + 2 Ё ( s — c ) ^jD , | ds = 0 e

L           j = ⁰             J

Ё у ' | D i — 2 Ё f j q^s ² ( s - c ^ds ^J D j КЕЛ J q¥ f ( s ) ds Ie i = 0     I          j = 0 V ,    ' !                  J J     i = 0     Г a    ' !              J

nbb

D_t — 2^     — ( s — c ) ^jdis Dj = J —— f ( s ) ds , i = 0, n .

'

J =0\a   '■                J

Если ввести обозначения в системе из n уравнений (4)

C 'J = J q i ( s ) ⁽ s — c ) j ds , i , j = 0, n , fi = f q i ^ s ) f ( s ) ds , i = 0, n , ^,J i                                                                                    ' !

aa

то получим систему линейных алгебраических уравнений относительно неизвестных D j , j = On :

n

D i -П C ,.j D j = f„ ' = 0. n .                          (6)

j = 0

Систему уравнений (6) можно переписать в матричном виде (7): n

D i — A S C ,,., D j = f , , ¹ = °. n . ( I - Ж ) D = f « D = ( I — A C ) — ‘ f ■           (7)

j = 0

Обратная матрица (I - AC)-1 в программе вычислялась библиотекой Msimsl на языке Fortran. Где: матричные элементы С и коэффициенты правой части (6) можно записать в виде г qt (s) /     v j    (Qt (c + У) j j         й i b — a r

С,j = 1 T(s - c) ds =1 —i—У dy,1, j = °,n, h =     .yg [—h, h], a i!                       - h      ,!                                             2

b q ( s )           h q, ( c + y )

^fi = [ — ^{f ( s} ) ^ds = J------- ^{f ( c +} У ) dy . i = °. n .

[         a     i ^-                      — h        ^{, !}

Во-первых. В формулах (8) переменная y g [-h, h] изменяет знак и принимает абсо- лютное значение меньшее, чем переменная x на отрезке [a, b], поэтому элементы матрицы Ci,j по модулю будут меньше чем, если использовать систему базисных функций

{Ai (y) = yi }^0, y g [-h, h] вместо системы функций {Ai (x) = xi |=0, x g [a, b] (в работе [1, стр. 137]). Это уменьшит норму матрицы С и расширит область невырожденности мат- рицы I — AC, то есть расширит область существования обратной матрицы (I - AC) 1.

Во-вторых. Базисные функции {Aj (y) = y' }^0 степенного вида не только входят множителями в разложение в ряд Тейлора (2) интегрального ядра K (x, s) по переменной x, но также обеспечивают корректность СЛАУ (4).

В-третьих. Решение (3) является функцией-полиномом степени n , которое можно сравнить с точным решением в каждой точке отрезка x g [ a , b ] в отличие от работы [9], где решение ищется в табличном виде (вектора) на узлах сетки.

В-четвертых. В работе [9, стр. 11] приведена интегральная квадратурная формула (9) для вычисления определенного интеграла с двенадцатым порядком погрешности, которая используется в данной работе для вычисления элементов матрицы и коэффициентов правой части системы (6) по формулам (8):

b

(y 1 ^, y 2 ) = J y 1 ⁽ x ) y 2 ⁽ x ) ^dx = ^{5 h} S ^C , y 1 ⁽ x ' ) y 2 ⁽ x i ) ^{+ 0(h 12} ) ’

1     7 Ь - a _ n1 = 1° p, h =-----, p g N ,

a где:

' = °

n i

	16067        .  _ -------, если i = 0 или i = n , 299376                   1 16067 -------, если ( i = 0mod 10 ) и ( 0 <  i <  n ), 149688       V             J   У         17 26575 ------, если ( i = 1 mod 10 ) или ( i = 9 mod 10 ), 74844       V            7     V            7
C i=\	—16175 , если ( i = 2 mod 10 ) или ( i = 8 mod 10 ), 99792 56^5 6237 , если ( i = 3 mod 10 ) или ( i = 7 mod 10 ), — 4825 ------, если ( i = 4 mod 10 ) или ( i = 6 mod 10 ), 5544 17807      -  < ------, если i = 5 mod 10. 12474

Таким образом, алгоритм (2)–(9) решает численно уравнение Фредгольма второго рода (1), обратная матрица ( I - AC )^{— 1} в формуле (7) вычислялась библиотекой Msimsl в компиляторе Fortran. Алгоритм (2)–(7) назовем решением интегрального уравнения Фредгольма (1) методом вырождения интегрального ядра.

Теорема 1 (критерий существования и единственности решения в алгоритме (2)– (7)). Для того чтобы алгоритм (2)–(7) имел единственное решение необходимо и достаточно, чтобы матрица I — A C была невырожденной.

Доказательство Теоремы 1 следует из формулы (7), в которой требуется существование обратной матрицы (I - AC) 1, что эквивалентно неравенству нулю определителя матрицы I — AC, det(I — AC) ^ 0 . Теорема 1 доказана. Здесь I - единичная матрица по- рядка n.

Теорема 2 (достаточные условия корректности алгоритма (2)–(7)). Пусть норма вектора f в уравнении (7) конечна. Если q = | A|||C || < 1, то алгоритм (2)-(7) корректен и

I ( I — A C )^{— 1} <  — =    ¹   .

1 — q i — A C

справедлива оценка нормы обратной матрицы

Доказательство. По условию теоремы 2 q = |A|||C|| < 1. Поэтому справедливо пред- ставление обратной матрицы рядом да

от

^да                     II                              II           да

(I — AC)—1 =£ AkCk, (I - AC)—1 = £ AkCk k=0           11                  11     k=0

< i wkiCf= k=0

¹— A l A ll

< да .

II D -| ( I ^{— a c ) — 1} f\ |<| I ^{— A} C pH f |< J A L

< да . Теорема 2 доказана.

Определение 1. Факториальной нормой

Чебышева вектор-функции назовем        число

f ( x ):[ a , b ] ^ C ( [ a , b ], R n ^{+ 1} ) f ( x ) = { f _} ( x ), f 1 (. x ),..., f_n ( x ) }

F            f_i ( x )

f = max x<0,b ]     i!

i = 0, n

F 1

Теорема 3. Выполнение условия q <  —j—----достаточно для корректности ал^{11 11} ”    2 ^ sh ( h )

горитма (2)-(7).

Доказательство. Пусть выполнены условия Теоремы 2 q = 12|||С|| < 1. Оценим бес- конечную норму матрицы C, используя формулу (8).

n

n

h

^

max 2 С , j\ = max IJ ⁱ = 0, n j = 0           ⁱ = 0, n j = 0 - h

= max

h

q i ^{( c} + y) i !

y j dy

.        1 h q ( ^c + y )

< I max- i=0,n i! J

j = 0

- h

i !

y j dy

<

<

n = 2 k

I max j = 0 i = 0, n ^{] u} y e [ - h , h ]

h

n = 2 k

h

1                ^h            n = 2 k f h                 г

-|qi ^{( c +} y )| J y^Jdy = I q L J y^Jdy = ²I q L ^{h +} i            - h          j = o       - h                V

h ³    h ⁵

--1---+... +

3!     5!

h ^{2 k + 1}   A

( 2 k + 1 )! J

h . . , . h² , h³ , h⁴ , h ⁵ ,        - h , h h²    h³    h ⁴     h ⁵ ,

Поскольку e — 1 + h +---1---1---1---+ ..., e — 1 — h +-----1-----+ ..., то

2!     3!    4!     5!                          2!    3!    4!    5!

e

h

-

e

h

= ²

V

h ³    h ⁵

h +--- 1--- + ...

3!    5!

h ³ h ⁵

о h + — + — +

3!    5!

e

h

-

e

- h

= sh ( h ).

Обозначим конечную сумму:

h ³ h ⁵           h ^{2 k + 1}

I n = 2 k = ^h + T + T + ... ⁺ ТУГ,   Tv I n = 2 k ⁺ R n = 2 k = ^{sh ( h} ), I n = 2 k <  ^{sh ( h} ), R n = 2 k >  ^0.

3!    5!          ( 2 k + 1 )!

2 2 k + 3       2k k + 5        2k k + 7       ^2 k + 9

Rn=2 k = sh(h) - In=2 k = (2 k + з), + (2 k + 5), + (2 k + 7)1 + (2 k + 9)1 + - = h + (1+<2k±3i h2h4+<2k+3> h 6 +1 -hk+3_.

( 2 k + 3 )! V    ( 2 k + 5 )!      ( 2 k + 7 )!      ( 2 k + 9 )!       '"J    ( 2 k + 3 )!

1 +

V

h ²      ₊____________ h4____________₊__________________h j___________________₊

<

( 2 k + 4 )( 2 k + 5 )⁺ ( 2 k + 4 )( 2 k + 5 )( 2 k + 6 )( 2 k + 7 )⁺ ( 2 k + 4 )( 2 k + 5 )( 2 k + 6 )( 2 k + 7 )( 2 k + 8 )( 2 k + 9 )⁺ ’"^

h² k ^{+ 3 (},J h Л ² ( h A ⁴ J h Л

( 2 k + 3)! [   V 2 k + 4 J   V 2 k + 4 J V 2 k + 4 J

A + ...

J

h ^{2 k + 3}

( 2 k + 3 )!

-

h

2 k + 4

h2 k+3           1                                    2kk+31

sh (h) - In=2 k < 7—T —-----о In=2 k ^ sh (h) -      —-y

( 2 k + 3 )!    ( h  A ²                      ( 2 k + 3 )^   ( h A 2

V 2 k + 4 J                             V 2 k + 4 J

Поскольку q = ^|| C || <  1 о | С | <  да также | С 1L <  2| \q\ L I n = 2 k <  Д ^{то ве}Р^ны оценки

F 1             1

< -гл----< -гл----<

“ 2| A\ sh ( h )   2| ^ I n = 2 k

V

sh ( h )

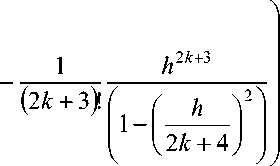
, n = 2 k .        (10)

Теорема 3 доказана.

Замечание. Отметим, что в правой части неравенства (10) обе оценки фактически совпадают, поскольку если положить n =2 k =10, h =π/2 добавочное слагаемое очень мало.

( 2 k + 3)!

h ² k ^{+ 3}

1      1.5713

(

1 - k

h

² Л 13! (

2 k + 4 J J

1 - k

1.57 ) ²

-----------------------------I

14 7

7 7

5.73 • 10 ^{- 8}.

Теорема 4

• 1)    Пусть C - положительная матрица, C i j >  0, i , J = 0, n и И >  0 (либо C - отрицательная матрица, C i , j <  0, i , J = 0, n и И <  0 ) с элементами главной диагонали n

^J = ^{0, J} * i

• 2)    Верна оценка для нормы обратной матрицы

1 4 I- W )-1l L

< — , r * = min 1 - И

n

\

r         i = 0, n

k

Z C ij i = 0      7

*

, ^r

n

max^{1 - W} Z C i , j .

i = 0, n

k       i = 0      7

Доказательство

1) По условию Теоремы 4

n

n

^{1 -} W| ^C i , i I >  И Z ^C i , J I, i = ⁰, ⁿ ^ И Z ^C i , J < ¹ ^ max

J = 0, j * i                           j = 0                 i = 0, ⁿ

n

I И Z G j - И C L <  1.

J = 0

По Теореме 2 алгоритм (2)-(7) корректен и существует обратная матрица ( I - W C ) ¹ с ограниченной нормой.

2)    Диагональные    элементы    матрицы

n

I - W C    положительны

¹ - И ^c i,i |> W Z C ,4 ⁰

, а недиагональные

отрицательны так как

—

^J = ^{0, J} * i

W C i , j <  0 V i , J = 0, n , i * J . Также по условию Теоремы 4 матрица I - W C имеет строгое

диагональное преобладание. Тогда выполнены все условия Теоремы Ю. С. Волкова, В. Л.

Мирошниченко [10] для матрицы монотонного вида I - W C и справедлива оценка

4 <| ( I - W C ) -¹|| <  4 r ¹¹                "“     r *

, r *

(.

= min 1

i = 0, n

k

-

n

^W Z C ij i = 0

к

*

> 0, r

n

= max 1 - W Z C i

Теорема 4 доказана.

Рассмотрим пример 1 .

i = 0, n

k

i , J

> 0.

i = 0      7

1 1

y ⁽ x ) ^-J e x s y ⁽ s ) ^ds = e x .

² 0

С точным решением y ( x ) = 2 e x . Выполним проверку:

1 1

1 x 1Г x - s    s i       x . .     x     x      x

2 e--e  2 e ds = e « 2 e - e = e .

² 0

Применим алгоритм (2)–(9) и достаточные условия корректности алгоритма (Теорему 3) к примеру (10), получим ( n = 20):

Л = 1/2, K(x, s) = ex-s, f (x) = ex, a = 0,b = 1, c = h = 1/2, Ki) (c, s) = qi (s) = Kxi) (1/2, s) = eш—s i = 0,n,s e [0,1],IIqllF <      -----О llqllF

^{11 11} ”    2| Л sh ( h )          "

I e ^{1/2 -} s|

= max ------- = e ^1/2

* < 0,1],     i !

i = 0, n

1.649 <-------1-------

2 • (1/2) sh (1/2)

* 1.919.

Таблица 1. Численное и точное решение примера (10). Число базисных функций n =20, число интервалов n = 10 в квадратурной формуле (9)

x	unum	uexact	num     exact u   — u
0.000000000000000E+000	2.00000000000000	2.00000000000000	8.88178419E-016
0.100000000000000	2.21034183615130	2.21034183615130	4.44089209E-016
0.200000000000000	2.44280551632034	2.44280551632034	-4.4408920E-016
0.300000000000000	2.69971761515201	2.69971761515201	4.44089209E-016
0.400000000000000	2.98364939528254	2.98364939528254	0.0000000000E+000
0.500000000000000	3.29744254140026	3.29744254140026	8.881784197E-016
0.600000000000000	3.64423760078102	3.64423760078102	8.881784197E-016
0.700000000000000	4.02750541494095	4.02750541494095	8.8817841970E-016
0.800000000000000	4.45108185698493	4.45108185698494	-8.881784197E-016
0.900000000000000	4.91920622231390	4.91920622231390	8.8817841970E-016
1.00000000000000	5.43656365691809	5.43656365691809	8.8817841970E-016

С нормой Чебышева [11] для невязки задачи (разности численного решения и точного решения) на узлах сетки квадратурной формулы:

num u

—

exact              num u      = max u,

С    i = 0, n J

—

u eac^ = 8.8817E- 016, x i = a + h • i , i = 0, n 1 .

По найденному решению (3), можно найти норму невязки в промежуточных узлах сетки, она равна num u

—

exact              num u      = max u,-

II С     i = 1, n 1 i

—

u i ^exact^ = 1.776E-015, x i = a + h • ( i — 1/2 ) , i = 1, n 1 .

Значения нормы невязки задачи показывают, что функциональное решение (3) имеет двойную точность, – дает 15 верных значащих цифр в решении (табл. 1).

Пример 2.

1 1

У ^{( x} ) ^— J ^e  У ^{( s} ) ^ds = ^e .

² 0

С

точным

решением

У ^{( x} ) =        ^e x

5 — e ²

.

Выполним

проверку:

4 _x

----2 e

5 — e ²

1 1     6 4 A                 4

— ¹ e x ^{+ s} |       | eds = e^x О

2^J₀ V 5 — e ² J               5 — e²

—

-     2

5 — e

( . 2 e

—

1 ^

v ² J

5- e y = 1 = 1 .

5 — e ²

Применим алгоритм (2)–(9) к примеру (12), получим

Л = 1/2, K(x , s ) = e^{x + s} , f ( x ) = e x , a = 0, b = 1, c = 1/2, K xi ) ( c , s ) = q i ( s ) = K i ) (1 /2, s ) = e ^{1/2 +} s .

Бесконечная норма матрицы C , вычисленная программой с числом базисных функций n = 20, равна

||C L = 3.39714811032309    , Л||C L = (1/2)3.3 9714811032309     = 1.69857405516155 > 1.

Поэтому достаточные условия в теоремах 2, 3, 4 не выполнены, и теоремы 2, 3, 4 к примеру 2 не применимы.

Таблица 2. Численное и точное решение примера (11). Число базисных функций n=20, число интервалов n_{ = 30 в квадратурной формуле (9)

x	u num	uexact	U num - u exact
0.000000000000000E+000	-1.67430141208924	-1.67430141208924	2.2204460492E-016
0.100000000000000	-1.85038922873402	-1.85038922873402	0.0000000000E+000
0.200000000000000	-2.04499636271726	-2.04499636271727	1.3322676295E-015
0.300000000000000	-2.26007050764560	-2.26007050764560	8.8817841970E-016
0.400000000000000	-2.49776419785038	-2.49776419785038	4.4408920985E-016
0.500000000000000	-2.76045635167479	-2.76045635167479	4.4408920985E-016
0.600000000000000	-3.05077608048818	-3.05077608048818	4.4408920985E-016
0.700000000000000	-3.37162900171635	-3.37162900171635	8.8817841970E-016
0.800000000000000	-3.72622631923734	-3.72622631923734	4.4408920985E-016
0.900000000000000	-4.11811696218917	-4.11811696218917	0.0000000000E+000
1.00000000000000	-4.55122310384550	-4.55122310384550	8.881784197E-016

C нормой Чебышева [11] для невязки задачи (разности численного решения и точного решения) на узлах сетки квадратурной формулы ||unum - u exact^£ = max| u imum — u iecact^ = 1.3322E-015, x i = a + h • i , i = 0л ? .

Пример 3.

1 n y (x) --J sin( x + s)y (s) ds = sin x + cos x.

проверку:

С точным решением   y ( x ) =---- ( sin x + cos x )   . Выполним

4 - n

—-— (sin x + cos x ) - — f sin( x + s ) ——— (sin s + cos s ) ds = ——— (sin x + cos x ) -

4 - n              2q        4 - n               4 - n

— [ (sin x cos s + cos x sin s ) | ——— | ( sin s + cos s ) ds = ——— (sin x + cos x ) -— (sin x + cos x ) — = 2^J₀                       ( 4 - n /           ’    4 - n             ’  4 - n            ⁷2

) = sin x + cos x .

Применим алгоритм (2)–(9) к примеру 3, получим

Л = 1/2, K ( x , s ) = sin( x + s ), f ( x ) = sin x + cos x , a = 0, b = п , c = п / 2, K xi ) ( c, s ) = q i (s ) = K xi ) ( п / 2, s ) = sin ( s + ( i + 1) ^П j , i = 0, n , s e [0, п ]. Бесконечная норма матрицы C , вычисленная программой с числом базисных функций n = 20, в примере 3 равна

||C [ = 1528.89560494716, Л|C L = (1/2)1528.89560494716 = 764.447802473580 > 1.

Поэтому достаточные условия в теоремах 2, 3, 4 не выполнены, и теоремы 2, 3, 4 к примеру 3 не применимы.

Таблица 3. Численное и точное решение примера (12). Число базисных функций n=20, число интервалов n 1 = 30 в квадратурной формуле (9)

x	num u	uexact	num     exact u   — u
0.000000000000000E+000	4.65979236632548	4.65979236632549	-2.66453525E-015
0.314159265358979	5.87168092602949	5.87168092602949	-2.66453525E-015
0.628318530717959	6.50880844628713	6.50880844628714	-3.55271367E-015
0.942477796076938	6.50880844628713	6.50880844628714	-1.77635683E-015
1.25663706143592	5.87168092602949	5.87168092602949	-1.77635683E-015
1.57079632679490	4.65979236632549	4.65979236632549	0.0000000000E+000
1.88495559215388	2.99177086312304	2.99177086312304	-8.881784197E-016
2.19911485751286	1.03089398294480	1.03089398294480	8.8817841970E-016
2.51327412287183	-1.03089398294480	-1.03089398294480	1.11022302E-015
2.82743338823081	-2.99177086312304	-2.99177086312304	0.000000000000E+000
3.14159265358979	-4.65979236632548	-4.65979236632549	1.776356839400E-015

C нормой Чебышева [11] для невязки задачи (разности численного решения и точного решения) на узлах сетки квадратурной формулы

||unum - u exact ||c = max| u inum - u iexact | = 1.7763E -015, x i = a + h • i , i = 0^.

Результаты

Впервые предложен модифицированный метод вырождения ядра для решения интегрального уравнения Фредгольма 2-го рода. Идея метода заключается в разложении интегрального ядра по переменной x в ряд Тейлора в середине отрезка интегрирования. Для метода доказаны три теоремы – достаточные условия корректности алгоритма (2)– (7) с оценкой нормы обратной матрицы в формуле (7). Кроме того, определена факториальная норма Чебышева вектор-функции. Впервые получено достаточное условие (10), связывающее факториальную норму системы функций из частных производных интегрального ядра c параметром λ.

Алгоритм (2)–(7) тестировался для трех примеров, в которых интегральное ядро имеет экспоненциальную особенность или периодическую смену знака.