Численное решение задачи о взаимодействии частично теплопроницаемых трещин в двухкомпонентном материале под действием теплового потока

DOI:

Слоистые композитные материалы, в частности биматериалы (двухкомпонентные материалы), используются при производстве изделий и конструкций, которые подвергаются механическим и тепловым нагрузкам. Наличие трещин, особенно межфазных, может влиять на эксплуатационные свойства этих материалов. Для исследования разрушения материалов и их соединений важным направлением является моделирование взаимодействия внутренних трещин с межфазной. Многочисленные исследования посвящены задачам взаимодействия трещин в однородном материале, обзор исследований можно найти в работе [6]. Системы термоизолированных трещин в биматериале под воздействием теплового источника и теплового потока были рассмотрены в работах [7; 8]. В работе [1] получены аналитические решения задач теплопроводности с помощью метода малого параметра для случая, когда длина межфазной трещины намного больше, чем длина внутренних трещин, а малый параметр – это отношение характерной длины внутренней трещины к межфазной. В работе [2] получены численные решения сингулярных интегральных уравнений задач теплопроводности под действием тепловых нагрузок для частного случая взаимодействия двух трещин и проведено сравнение с аналитическим решением.

В данной работе рассматривается задача о взаимодействии частично теплопроницаемых трещин, когда биматериал находится под действием теплового потока. При численном решении данной задачи сделан параметрический анализ влияния близко расположенных внутренних трещин на коэффициенты интенсивности теплового потока (KИТП) [4] в вершинах межфазной трещины. Рассматриваются разные сочетания материалов.

1. Формулировка задачи

Рассмотрим двухкомпонентный материал (биматериал) с разными коэффициентами теплопроводности k ₁ и k ₂, находящийся под действием теплового потока интенсивностью q . На границе раздела материалов выполняются условия идеального контакта, за исключением участка, где расположена межфазная трещина длиной 2 a ₀. Один из материалов D ₁ ( y > 0) содержит внутренние трещины длиной 2 a_k (рис. 1).

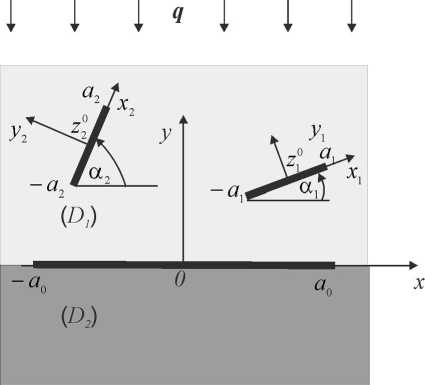
Рис. 1. Межфазная и внутренние трещины под действием теплового потока

Рассматриваем модель частично теплопроницаемых трещин [5]. Коэффициент теплопрони-цаемости поверхностей трещин является функцией, изменяющейся от 0 до 1 ( 0 ≤ η ( x ) ≤ 1 ); η ( x ) = 0 соответствует случаю теплоизолированных трещин; η ( x ) = 1 – случаю полностью теплопроницаемых трещин. В данной работе рассматриваем случай η( x ) = const.

В рассматриваемой задаче неизвестными будут γ _к ′ ( t ) – производные скачков температуры на линиях трещин, где 2 γ _к = T_k ⁺ –T_k ^- . Здесь и далее знаками «+» и «–» обозначены граничные значения, принимаемые функциями соответственно на верхнем и нижнем краях трещин. Система сингулярных интегральных уравнений для определения неизвестных γ ′ _к ( t ) на линиях теплопроницаемых трещин получена в работе [1]. Для одной межфазной и двух внутренних трещин система уравнений задачи будет иметь следующий вид:

^{a 0} γ′ ( t )                         ^{a 1                                              a 2}

0   dt+(1-η0(x))   P01(t, x)γ1′(t)dt +(1- η0(x))   P02(t,x)γ′2(t)dt= t-x

- a ₀                                 - a ₁                                            - a ₂

1π

q ₀( x )(1 -η ₀( x ))(1 + k ₁ /k ₂),

2 k ₁

x <  a ₀ ,

a0

(1 - η ( x ))     ²         P 10 ( t, x ) γ 0 ′ ( t ) dt +   ^{γ 1( t )} dt +

1+k /kt

1     2 - a0

a ₂

+ ∫ P ₁₂( t,x ) γ′ ₂( t ) dt = _k q ₁( x )(1 - η ( x )),                  I x I <  a ₁ ,

-a21

(1 - η ( x ))

1 + k ₁ / k ₂

a 0                                     a 1

∫ P ₂₀( t, x ) γ ₀ ′ ( t ) dt + ∫ P ₁₁( t,x ) γ ₁ ′ ( t ) dt +

- a ₀                             - a ₁

+   γ2(t)dt = π q2(x)(1- η(x)), t-x k

- a                    1

I ^x I <  a ₂,

где P_nk – регулярные ядра, содержащие геометрию задачи,

P nk ( t , x ) = Re[ _{tei α}

iαn e                   ].

+ z ⁰ - xe^{i α n} - z ⁰ kn

Система уравнений дополняется условиями ak

∫ γ′ k ( t ) dt = 0 , k = 0, 1, 2,                                         (5)

-ak обеспечивающими однозначность функции γk′ при обходе контура трещин.

В уравнениях (1)–(3) q ₀( x ) и q_n ( x ) ( n = 1, 2) определяли по формулам:

∂ T_j ⁰ q ₀( x ) = - k_j ∂ y

∂ T_j ⁰ , q_n ( x_n ) =- k_j

∂ y_n

,

₀                                                              y                                 y_n = 0

где T_j ( x , y ) – температурное поле в бездефектном материале, и в случае воздействия теплового потока

y = 0

интенсивности q функция T_j ⁰ имеет вид T_j ⁰ ( x , y ) = qy / k_j ( j = 1, 2).

2. Численное решение задачи

Решение системы сингулярных интегральных уравнений (1)–(3) получено численным методом механических квадратур [3]. Уравнения (1)–(5) приводим к безразмерному виду (подробности см. в [1]). Неизвестные функции в уравнениях (1)–(3) представим в виде

γ ^' _n ( ξ ) =

u_n ( ξ )

V1-ξ ²

где u_n ( ξ ) – новая неизвестная регулярная функция на отрезке [-1,1], 1 / V 1 - ξ ² – весовая функция, которая учитывает корневую особенность решения задачи о трещинах.

Используя квадратурные формулы для интегралов [3], уравнения (1)–(3) сводятся к системе 3 × М (3 – количество трещин; M – число узлов) алгебраических уравнений для определения 3 × М неизвестных u_n ( t_m ) (более общее численное решение получено в работе [2]):

1 M 2

∑ ∑ [ u_k ( t_m ) P_nk ( t_m,x_r )] =π q_n ( x_r ) ,                               (8)

M m = 1 k = 0

M

У U n ( t m ) = 0, n = 0, 1, 2; r = 1, 2, ., M - 1,                          (9)

m = 1

где                t _m = cos- M -^- n ( m = 1, 2,    , M) ; x r = cosM ( r = 1, 2,..., M - 1).              (10)

Здесь P_nk – дискретный аналог регулярных ядер (4) вместе с сингулярной частью, которая получается из (4) при n = k .

Таким образом, для системы сингулярных интегральных уравнений (1)–(3) построена соответствующая система алгебраических уравнений (8)–(9). После решения системы (8)–(10) определяем нормированные коэффициенты интенсивности тепловых потоков в вершинах (KИТП) трещин

К ±

■     ^ = ц U n ( ± 1) ( n = 0, 1, 2).                                   (11)

aqk n 1

Здесь верхний знак относится к КИТП тепловых потоков в правой вершине трещины ( K Tn ), а нижний - к левой ( K Tn ). Величины u_n ( ± 1) определяются выражениями [3]

MM

U . (1) = й У ( - 1) m "u. ( t m ^ — П ; U . ⁽ - 1) = ^ У ⁽ - 1) M + m u . ⁽ t m ^ П . m = 1                                                             m = 1

Численное решение справедливо для близкого расположения трещин и для сопоставимых размеров трещин. Для трех трещин имеем систему 3 х М алгебраических уравнений, где M -число интерполяционных узлов; для хорошей точности решения брали M = 70.

KИТП (11) вводятся по аналогии с коэффициентами интенсивности напряжений в упругих задачах о трещинах [1; 4] и являются локальными характеристиками распределения тепла в окрестностях вершин трещин.

3.    Параметрический анализ результатов

На рисунках 2–4 показаны графики зависимости нормированных KИТП в вершинах межфазной трещины от координаты центров внутренних трещин (рис. 2) и от угла наклона трещин (рис. 3 и 4). Графики получены при условии, что коэффициент теплопроницаемости межфазной трещины равен п ₀ = 0,5 , а коэффициенты теплопроницаемости внутренних трещин -П 1 = {0; 0,4; 0,8} . Межфазная трещина с центром в точке z 0 = 0 имеет длину 2 а ₀ = 2. Следует отметить, что все величины представлены в безразмерном виде, z_k ⁰ / a ₀ и a_k / a ₀ ( k = 0, 1, 2), однако обозначения для них оставили прежние.

На рисунке 2 внутренние трещины c длинами 2 а 1 = 2 a ₂ = 0,6 расположены параллельно к межфазной трещине и находятся на расстояниях от нее У 0 = 0,5 , у 0 = 1,2 в материале ( D 1 ). Рисунки 2 и 3 соответствуют случаю, когда материал ( D ₁) имеет свойства материала SiC , а материал ( D ₂) - свойства TiC , тогда к 1 / к ₂ = 3 (см. таблицу).

Из рисунка 2 следует, что максимальное влияние происходит, когда внутренние трещины имеют координату x ⁰ = 0,9. Поэтому для более подробного анализа взаимодействия трещин на рисунках 3 и 4 рассматриваем случаи, когда внутренние трещины расположены в точках z 0 = 0,9 + 0,5 i , z 0 = 0,9 + 1,2 i материала ( D 1 ).

Из рисунка 3 следует, что при разных коэффициентах теплопроницаемости поверхности внутренних трещин ( п 1 ) значительно изменяется КИТП в правой вершине межфазной трещины. Максимальное изменение наблюдается в случае, когда внутренние трещины параллельны межфазной (а 1 = 0⁰ ), и это изменение отсутствует при а 1 = 76 0 .

На рисунке 4 рассматривается влияние двух внутренних трещин на межфазную трещину, когда материал ( D ₁) имеет свойства материала TiC , а материал ( D ₂) – свойства SiC , тогда к 1 / к ₂ = 0,33 (см. таблицу).

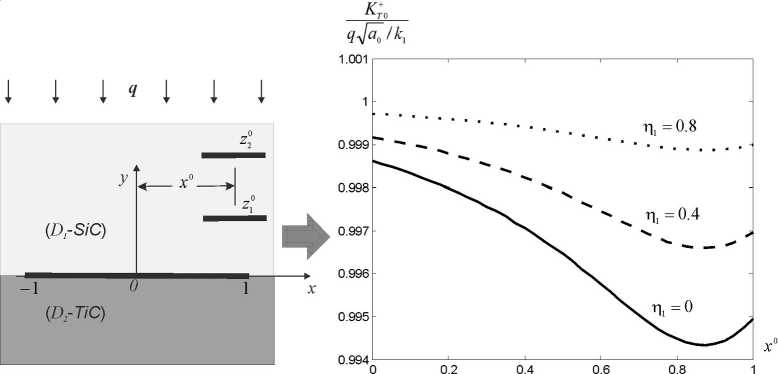
Рис. 2. Графики зависимости нормированного KИТП в правой вершине межфазной трещины от координаты x 0 горизонтального перемещения центра внутренних трещин при п ₀ = 0,5 - z ” = x ⁰ + 0,5i , z 20 = x ⁰ + 1,2 i

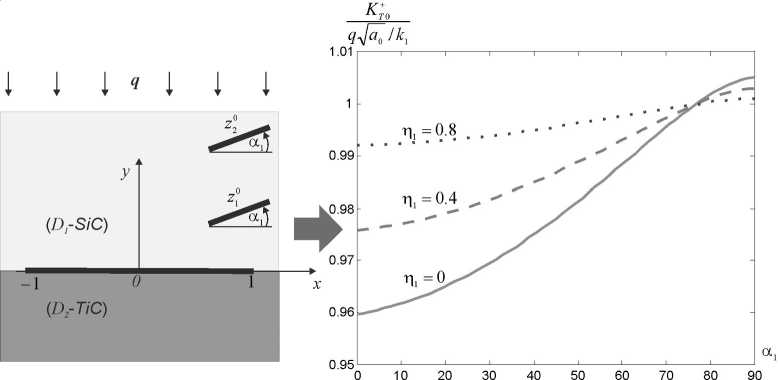
Рис. 3. Графики зависимости нормированного KИТП в правой вершине межфазной трещины от угла наклона внутренних трещин а 1 при п ₀ = 0,5 - z 1⁰ = 0,9 + 0,5 i , z 0 = 0,9 + 1,2 i , k ₂ / k 1 = 3

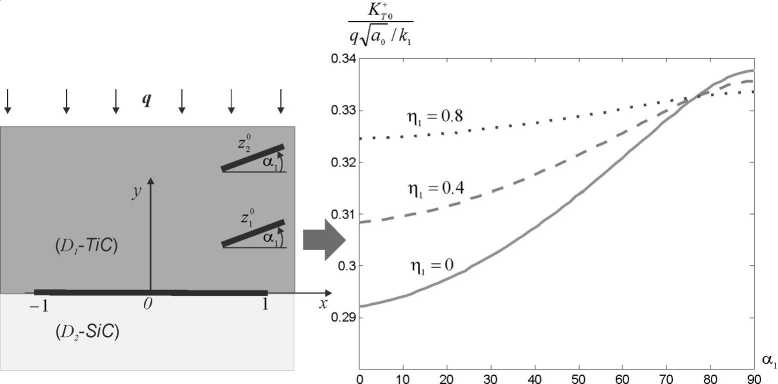
Рис. 4. Графики зависимости нормированного KИТП в правой вершине межфазной трещины от угла наклона внутренних трещин а 1 при п ₀ = 0,5 - z ” = 0,9 + 0,5 i , z 0 = 0,9 + 1,2i , k 1 / k ₂ = 0,33

Из рисунка 4 видно, что KИТП численно уменьшается при уменьшении k ₁ / k ₂ , но его характер изменения остается таким же.

В таблице приведен анализ численного значения нормированного KИТП в правой и левой вершинах межфазной трещины при наличии внутренних трещин, при разных сочетаниях материалов. Геометрическое расположение и параметры трещин такие же, как на рисунках 3 и 4. Рассматривается случай коллинеарных трещин, то есть α ₁ = 0⁰ . Коэффициент теплопроницаемости межфазной трещины равен 0,5, а коэффициент теплопроницаемости внутренних трещин – 0,4.

D 1 / D 2 – сочетание материалов	k 1 / k 2	+ K T 0 q a 0 / k 1	- K T 0 q a 0 / k 1	± K T 0 q a 0 / k 1	Δ K + , %	∆ K - , %
SiC / TiC	60/20	0,9753	1,0016	1	-2,47	+0,16
TiC / SiC	20/60	0,3077	0,3342	0,3325	-7,46	+0,51
Al 2 O 3 / SiC	18/60	0,3002	0,3267	0,325	-7,63	+0,52
TiC / ZrO 2	20/2	2,7254	2,7516	2,75	-0,89	+0,06
TiC / Al 2 O 3	20/18	0,5028	0,5292	0,5275	-4,68	+0,32
SiC / ZrO 2	60/2	7,7254	7,7516	7,75	-0,32	+0,02

+

Таким образом, kj – коэффициент теплопроводности материалов (Вт/(м*K)).   KT0   – q a0 /k1

- нормированный KИТП в правой вершине межфазной трещины. KT0 – нормированный KИТП q a /k

K ′ ±                                 0 1

в левой вершине межфазной трещины.    T0  – нормированный KИТП в левой и правой вер- q a0 /k1

шинах межфазной трещины при отсутствии внутренних трещин [1]:

±

K_{T 0}

q a ₀ / k ₁

= (1 -η 0 ) ¹₂( m + 1) , где η ₀ = 0,5 , m = k ₁/ k ₂.

∆ K ^± – уменьшение или увеличение (отличие в %) нормированного KИТП в вершинах межфазной трещины при наличии внутренних трещин вычисляли по формуле:

∆K± =

±±

K T 0         K T 0

- q a0 / k1    q a0 / k1

× 100%,

±

K T 0

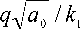
Из таблицы следует, что наличие внутренних трещин может как увеличивать, так и уменьшать KИТП по сравнению с коэффициентами для одной межфазной трещины.

Заключение

В работе исследовано влияние взаимодействия трещин на тепловые потоки в биматериале. Показано значительное влияние тепловых характеристик биматериала, а именно, коэффициентов теплопроницаемости трещин и тепловых свойств материалов, и геометрических углов наклона внутренних трещин и их расположения на коэффициенты интенсивности тепловых потоков в вершинах межфазной трещины. Изменение коэффициента интенсивности теплового потока в вершинах межфазной трещины приводит к существенной неоднородности тепловых полей в этих областях, что, в свою очередь, приводит к нарастанию деформаций и соответствующих напряжений на границе соединения материалов.