Численное решение задачи оптимизации для определения параметров установки фиксаторов с памятью формы

Среди травм лицевого черепа переломы нижней челюсти возникают в 70–80% случаев. По мнению авторов, использование фиксаторов, изготовленных из сплавов с памятью формы, является наиболее предпочтительным, так как установка скобок простой конструкции не требует значительного повреждения костной ткани. Эти фиксаторы также обладают хорошей биосовместимостью [1, 5, 12, 14].

Изучению эффективного остеосинтеза при установке имплантатов с памятью формы, применяемых в челюстно-лицевой хирургии и стоматологии, в последнее время уделяется всё большее внимание. В работе [14] приведены результаты лечения 77 пациентов разного возраста. Скобы использовались для восстановления одиночных переломов (56 пациентов) и множественных переломов (21 пациент). В результате полное залечивание наблюдалось в 72 случаях. В статьях [10, 11] проводится гистологический анализ ткани при установке имплантатов для регенерации нижнечелюстной кости. Подобное исследование по биосовместимости имплантатов, установленных в слуховых косточках крыс, проведено in vivo в работе [16]. Отмечено,

Селянинов Александр Анатольевич, профессор кафедры теоретической механики, Пермь

Рис. 1. Общий вид фиксатора ( а ) [5] и муфты ( б ) [2]

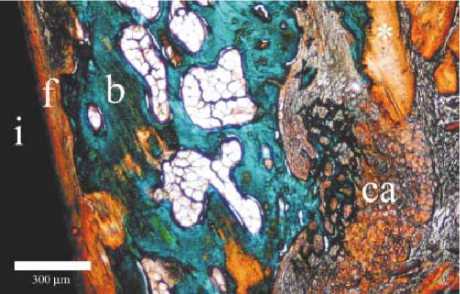
Рис. 2. Соединительная ткань между имплантатом и костной тканью [16]: i – имплантат, f – фиброзная ткань, b – новообразованная кость, ca – хрящ что на «приживаемость» имплантата влияют предварительная термообработка и химический состав фиксатора [15].

В работе [2] с помощью метода инфракрасной термографии получены результаты для фиксаторов из сплава никелида титана ТН–1ХЭ и ТН–1А (рис. 1), которые могут устанавливаться как с пористыми муфтами, предназначенными для уменьшения механических нагрузок, так и без них. В монографии [7] рассматриваются различные виды остеосинтеза устройствами из никелида титана при повреждениях и заболеваниях лицевого черепа.

Биомеханический анализ поведения фиксатора в костной ткани проводился в работах [4, 6]. Решению задачи управления напряжениями, которые скобка создаёт при установке в костную ткань в результате фазовых превращений, посвящена работа [4]. В работе [6] рассмотрена задача о взаимодействии имплантата с костной тканью. Задача решалась с применением программы ANSYS .

По мнению авторов, для достижения эффективного остеосинтеза костной ткани при установке фиксаторов хирургу необходимо знать положения крепления скобок и усилия, развиваемые фиксаторами, способствующие наискорейшему росту кости. Субъективные способы решения данной задачи не всегда приводят к положительному результату (7–12% случаев осложнений [20]) и не всегда учитывают индивидуальные особенности пациентов.

С точки зрения биомеханики, при сращивании перелома большое значение имеет распределение напряжений, способствующих росту с костной ткани на границе перелома костной ткани. Данная работа посвящена определению параметров установки фиксаторов из сплавов с памятью формы. Под параметрами понимаются точки установки фиксаторов и усилия, которые должны создавать фиксаторы для наискорейшего роста костной ткани (т.е. для создания «оптимальных» напряжений на границе перелома).

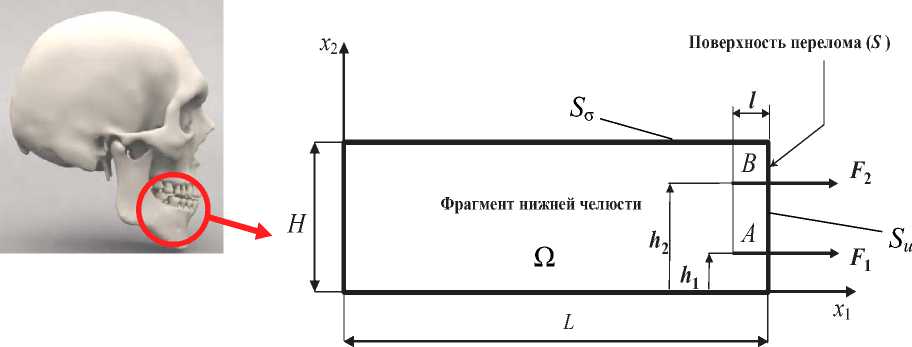
Рис. 3. Расчётная схема

Таким образом, задача эффективного остеосинтеза перелома с точки зрения биомеханики должна рассматриваться как задача оптимизации распределения напряжений на границе перелома в зависимости от положения фиксаторов и усилий, создаваемых ими.

Постановка задачи

Формулировка задачи минимизации

Рассмотрим фрагмент нижней челюсти, который моделируется как прямоугольник, длина которого равна L , а высота H (рис. 3). В точках А и В устанавливаются фиксаторы, изготовленные из сплавов с памятью формы. Усилия, развиваемые фиксаторами, обозначены как F ₁ и F ₂ .

Параметрами установки фиксаторов являются:

• •    l - расстояние от границы перелома до точек установки фиксаторов (считается известным);

• •    h , и h ₂ - высоты установки фиксаторов.

Необходимо определить положения установки фиксаторов, то есть величины h ₁ , h ₂ , F ₁ , F ₂ .

Далее необходимо сформулировать критерии оптимальности: в состоянии покоя (т.е. при отсутствии жевательных нагрузок) нормальные напряжения должны быть равномерно распределены по сечению и равны оптимальному значению о * .

Данное условие можно записать в виде функционала следующего вида:

J = f(« n ( h , , h 2 , F 1 , F 2 ) -о * ) ² dS ^^цц >  inf,                    (1)

1 ^, 2 ^, 1 ^, 2

S где оn (h,, h2, F,, F2) - нормальные напряжения на границе перелома, о* - напряжения, способствующие наискорейшему росту.

Нормальные напряжения на границе находятся по формуле [8]

о _n = о ,, cos ² а + о ₂₂ sin ² а + о ₁₂ sin 2 а ,                          (2)

где α – угол наклона нормали к границе элемента относительно оси x 1 .

Компоненты вектора напряжений находятся из решения задачи о напряженно-деформированном состоянии кости.

Согласно [13], для кортикальной кости оптимальными являются сжимающие напряжения

σ ^* = 2 МПа .                                  (3)

При формулировке критериев преследуются следующие цели:

• 1.    для предотвращения чрезмерного сжатия фрагментов, необходимо, чтобы усилия фиксаторов были больше нуля по абсолютной величине и меньше предельных значений F max ;

• 2.    чтобы избежать близкого расположения фиксаторов, расстояние между точками А и В должно превышать величину a .

• 3.    точки крепления должны находиться на расстоянии не ближе a /2 от края челюсти.

Первое условие формулируется следующим образом

F>F>0F>F>0 max >1 >0, max >2 >0.( )

Предельные значения F _max для кортикальной и губчатой костных тканей найдены в работе [6].

Второе ограничение записывается в следующем виде:

h2- h1-a>0 .(5)

Третье ограничение можно записать следующим образом:

h1>a2;h1

В работе принималось a =6 мм.

Постановка задачи о напряженно-деформированном состоянии нижней челюсти

Наиболее полно постановка задачи о расчете напряженно-деформированного состояния биологических объектов представлена в [17, 18, 19]. В данной работе рассматривается упрощенный вариант постановки.

Обозначим область, занимаемую фр а гментом нижней челюсти как Ω . Замыкание области границей обозначим как Ω , границу челюсти, которая считается достаточно гладкой – S ( Ω=Ω∪ S ). Тогда краевая задача определения компонент тензора напряжений в нижней челюсти задается следующими уравнениями: • уравнения равновесия

∫σ⋅⋅ε(w)dΩ-∫b(F1,F2)⋅wdΩ=0,(7)

ΩΩ для ∀w∈(W21(Ω))3и w=0 r∈Su ; здесь b(F1,F2)∈ (L2(Ω))3 – объемные силы;

• •    геометрические соотношения Коши

ε=2(∇u+∇uT),r∈Ω,(8)

где u ∈ ( W ₂ ¹ ( Ω )) ³ , а производные понимаются в обобщенном смысле.

• •    закон Гука для изотропного тела

σ= λθI1(ε)+2µε,r ∈Ω.(9)

Граница S разделена на две непересекающиеся части: S = S u + S _о . Кинематические граничные условия заданы на части границы S u , а граница S _с свободна от напряжений.

• •    Граничные условия имеют вид:

  
  
  
  

u = 0, r G Su , n • О = 0, r G So

Решение задачи проводилось с помощью программы, написанной в пакете MatLab 6.5. В программе одновременно реализовывались два метода: метод конечных элементов для определения напряженно-деформированного состояния нижней челюсти и метод оптимизации – метод минимизации по правильному симплексу [3].

Перед началом решения задачи оптимизации были построены зависимости значений функционала J от параметров h ₁ и F ₁ . (рис. 4, 5). Аналогичные зависимости могут быть получены для h ₂ и F ₂ . Как видно из рис. 4, плотность разбиения области, занимающей фрагментом нижней челюсти, не влияет на поиск минимума.

Далее рассмотрим напряженно-деформированное состояние при наличии перелома, находящегося в самом опасном месте (рис. 6, а ). В качестве репрезентативных были рассмотрены три вида переломов: прямой, криволинейный, косой. Схема и параметры установки фиксаторов для данных видов переломов показаны на рис. 6, б .

На рис. 7 показано распределение напряжений на границе S u для случая прямого перелома. Параметры установки фиксаторов для этого случая приведены в табл. 1.

В случае криволинейного перелома при l <0,9 см функция J ( h 1 ) не является гладкой. Это обусловлено тем, что вблизи границы перелома нельзя достичь равномерности распределения напряжений.

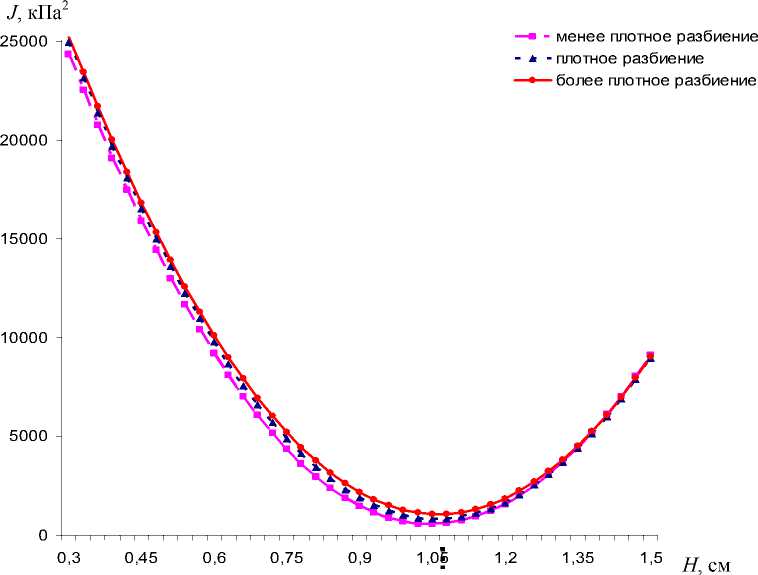
Рис. 4. Распределение значений функционала J ( h 1 ) при различном количестве разбиений сетки при фиксированных параметрах ( h 2 = 2 см, F 1 =5 Н, F 2 =5 Н)

J , кПа²

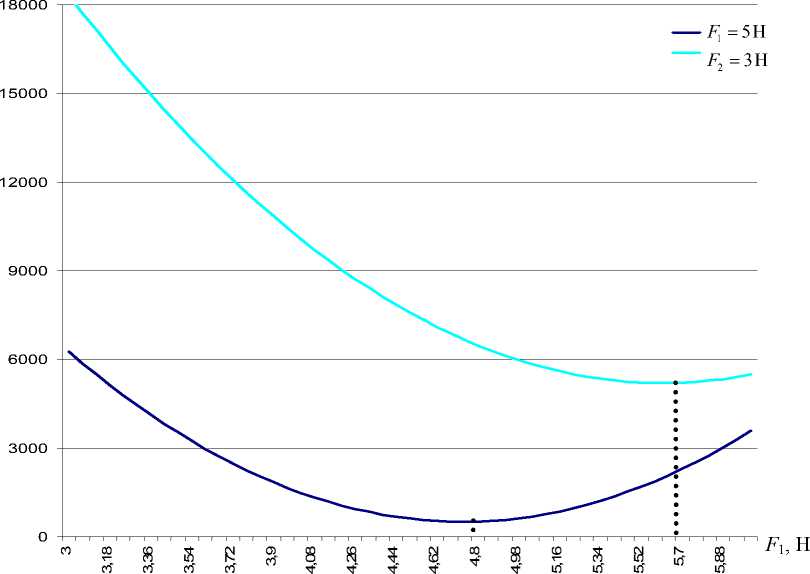
Рис. 5. Распределение значений функционала J ( F 1 ) при фиксированных параметрах ( h 1 = 1 см, h 2 = 2 см, F 2 =3 Н – светлая линия; h 1 = 1 см, h 2 = 2 см, F 2 =5 Н – тёмная линия)

а

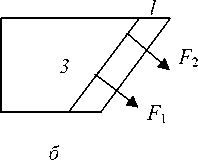
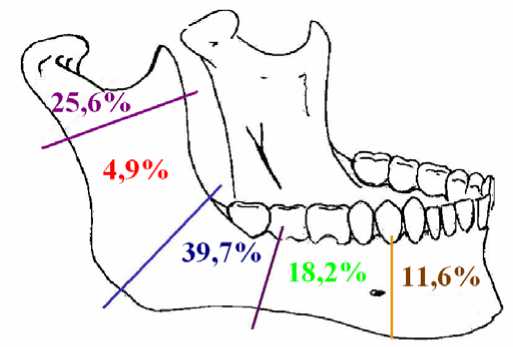
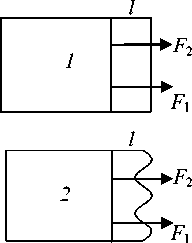
Рис. 6. а – частота локализации переломов нижней челюсти; б – модели переломов: 1 – прямой; 2 – криволинейный; 3 – косой

На рис. 8 показано распределение напряжений на границе S u для случая криволинейного перелома. Параметры установки фиксаторов для этого случая приведены в табл. 2.

На рис. 9 показано распределение напряжений на границе S u для случая косого перелома. Параметры установки фиксаторов для этого случая приведены в табл. 3.

Характерным для графиков является наличие краевых эффектов, возникающих в окрестностях крайних точек фрагмента нижней челюсти.

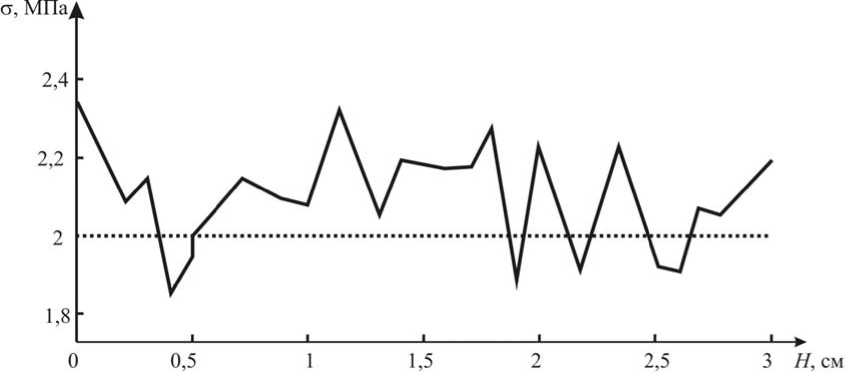
Рис. 7. Распределение напряжений в области перелома при установке фиксаторов ( l =1 см, h 1 =0,76 см, h 2 =2,23 см, F 1 = 4,88 Н, F 2 = 4,79 Н), пунктирная линия – оптимальные напряжения, способствующие росту костной ткани

Таблица 1

Результаты решения задачи оптимизации для случая прямого перелома

l , см	h 1 , см	h 2 , см	F 1 , H	F 2 , H
0,3	0,87	2,18	2,70	2,27
0,4	0,62	2,12	3,62	3,00
0,5	0,63	2,12	3,88	3,69
0,6	0,63	2,14	4,01	4,20
0,7	0,66	2,17	4,36	4,66
0,8	0,74	2,21	4,67	4,55
0,9	0,71	2,18	4,61	4,94
1	0,76	2,23	4,88	4,79
1,1	0,83	2,16	4,67	4,57
1,2	0,87	2,15	4,78	4,57
1,3	0,87	2,12	4,77	4,76
1,4	0,86	2,19	5,01	4,74
1,5	0,93	2,19	5,22	4,41

Полученные результаты можно использовать для разработки практических рекомендаций врачам.

Заключение

В данной работе приведено решение задачи, связанной с установкой фиксаторов из сплавов с памятью формы, которая является частью практических рекомендаций врачам с целью избежания осложнений, возникающих в результате хирургического вмешательства. Методика включает в себя определение точек установки фиксаторов,

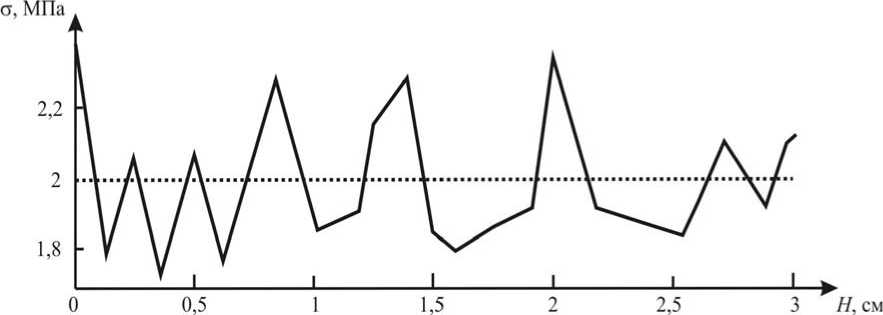
Рис. 8. Распределение напряжений в области перелома при установке фиксаторов ( l =1,3 см, h 1 =0,56 см, h 2 =2,62 см, F 1 = 5,28 Н, F 2 = 4,95 Н), пунктирная линия – оптимальные напряжения, способствующие росту костной ткани

Рез ультаты реш l, см ения задачи опт h1, см имизации для с h2, см лучая криволи F1, H Таблица 2 нейного перело F2, H ма 0,9 0,59 2,67 5,43 4,66 1 0,56 2,72 5,39 4,66 1,1 0,59 2,40 4,74 5,15 1,2 0,81 2,25 4,84 4,47 1,3 0,56 2,62 5,28 4,95 1,4 0,87 2,17 4,87 4,64 1,5 0,62 2,60 5,38 4,77 способствующих оптимальному росту костной ткани и созданию фиксатором усилий при установке в костную ткань, что позволяет разрабатывать объективные подходы к выбору фиксаторов с эффектом памяти формы для каждого пациента, рассчитывать напряженно-деформированное состояние в области роста, а также формулировать и решать задачи оптимизации ростовых процессов. Кроме того, методика учитывает индивидуальные особенности пациента (например, вид и локализацию перелома нижней челюсти, влияющие на распределение напряжений в области перелома; возраст пациента, определяющий величину создаваемых усилий).

В работе представлено решение задачи оптимизации о нахождении позиций установки фиксаторов и усилий, создаваемых фиксаторами таким образом, чтобы напряжения на границе перелома были наиболее близки к оптимальным. Задача формулируется как задача минимизации некоторого функционала с рядом ограничений. В целевую функцию входят функционал распределения напряжений на границе перелома. Задача оптимизации решалась в программе, написанной в пакете MatLab , методом минимизации по правильному симплексу; при решении учитывалось напряженно-деформированное состояние нижней челюсти.

В результате в работе получены значения параметров установки скобок для различных видов переломов (прямолинейный, криволинейный, косой) нижней челюсти.

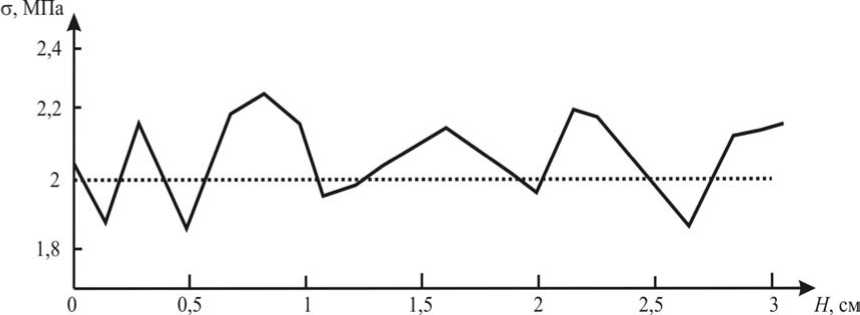
Рис. 9. Распределение напряжений в области перелома при установке фиксаторов ( l =1 см, h 1 =0,92 см, h 2 =2,36 см, F 1 = 5,23 Н, F 2 = 4,94 Н), пунктирная линия – оптимальные напряжения, способствующие росту костной ткани

Таблица 3

Результаты решения задачи оптимизации для случая косого перелома

l , см	h 1 , см	h 2 , см	F 1 , H	F 2 , H
0,3	0,87	2,15	3,76	3,55
0,4	0,41	2,16	3,05	3,33
0,5	0,68	2,15	4,08	4,35
0,6	0,82	2,24	4,64	4,50
0,7	0,87	2,12	5,05	4,88
0,8	0,89	2,37	5,17	4,63
0,9	0,87	2,31	4,69	4,86
1	0,92	2,36	5,23	4,94
1,1	1,01	2,48	5,57	4,65
1,2	1,28	2,62	6,63	2,53
1,3	1,12	2,66	6,01	3,77
1,4	1,11	2,51	5,49	4,74
1,5	1,62	2,31	5,92	5,49

Благодарности

Работа выполнена в рамках Соглашения о сотрудничестве между Венским техническим университетом и Пермским государственным техническим университетом. Работа выполнена при поддержке РФФИ в рамках проектов № 07–01– 96061-р-Урал-а, 07–01–92168-НЦНИ_а.