Численное решение задачи течения несжимаемой жидкости в плоском канале с обратным уступом при больших числах Рейнольдса

В силу вышеуказанных причин рассматриваемая задача является практически идеальной для тестирования и демонстрации возможностей новых вычислительных технологий, разрабатываемых для моделирования отрывных течений в полуоткрытых областях. Соответственно в литературе можно найти большое количество работ, посвященных изучению несжимаемых течений вязкой жидкости в плоском канале с обратным уступом в двумерном приближении. Большинство из них выполнено для чисел Рейнольдса, не превышающих Re = 1000 (здесь и далее число Рейнольдса строится по полной высоте канала и среднемассовой входной скорости потока) [1–14]. Однако существует несколько публикаций, в которых стационарное решение задачи найдено для более высоких значений Re , вплоть до 3000 [15–21]. И совсем немного статей посвящены задачам при значениях числа Рейнольдса меньше единицы вплоть до Re = 10 - 4 [6, 22, 23]. Основной их целью было получение вихрей Моффатта [24] у основания уступа, поскольку при столь низких значениях Re эффект инерции потока пренебрежимо мал по сравнению с вязкими силами и, следовательно, в этом месте движение жидкости имеет чисто стоксовский характер.

Что касается влияния параметра расширения потока ER , то его изучение проведено в ограниченном числе публикаций [5, 6, 8, 10, 23], причем диапазон изменения ER обычно невелик и укладывается в промежуток 1,17 <  ER <  3,0 . Исключение составляют следующие статьи: [4], в которой 1,33 <  ER <  4,0 ; [21], в которой 1,43 <  ER <  5,0; [12], в которой 1,11 <  ER <  10,0. В этих работах авторы, как правило, делали вывод о прямой зависимости длины первичного вихря за уступом — x ₁ , от величины ER : чем больше ER , тем больше x ₁ . Однако в [12, 21] показано, что эта зависимость немонотонная и имеет место максимум значения х 1 при ER ® 2,5 + 3,0 для Re <  1000.

Относительно влияния других параметров задачи, таких как общая длина канала или длина входного участка, мнения исследователей расходятся. В [1, 3, 5, 18, 23] длина входного участка обнуляется, так как их авторы считают, что параметры потока во входном участке не изменяются. Иными словами, граничные условия для втекающей жидкости, известные на большом удалении от уступа, можно сразу располагать в сечении внезапного расширения канала. Однако в большинстве публикаций полагается, что изменяющиеся параметры течения перед обратным уступом влияют на решение задачи в целом (см., например, [2, 8–16, 20, 21]).

В представленных в настоящем обзоре работах [15, 17, 19, 21, 25] анализируются как численные, так и экспериментальные результаты. Достаточно подробные измерения параметров ламинарного, переходного и турбулентного режимов течений в плоском канале за обратным уступом были выполнены в [15]. Исследования проведены для ER = 1,9423 и чисел Рейнольдса до значений порядка 8000. Кроме распределения компонент скорости потока в нескольких поперечных сечениях, также выявлена зависимость длины первичного вихря за уступом от Re. Показано, что при Re = 400 ^ 500 начинают проявляться признаки трехмерности движения жидкости. При этих же значениях числа Рейнольдса около верхней стенки канала возникает вторичный вихрь.

Общепризнано, что моделирование реальных двумерных ламинарных течений в канале с обратным уступом с помощью уравнений Навье-Стокса возможно только при числах Re <  400 ^ 600 [15, 17, 19, 21, 25]. Тем не менее существуют работы, в которых приводятся имеющие модельный характер решения уравнений Навье–Стокса для рассматриваемой задачи при числах Re , значительно превышающих данный предел [7, 10, 16, 20, 21]. Объясняется это тем, что с увеличением числа Рейнольдса резко возрастает сложность численного построения решений уравнений Навье–Стокса, обусловленная, прежде всего, неустойчивостью существующих алгоритмов. Для выхода из этой ситуации необходимо совершенствовать существующие, либо создавать новые вычислительные технологии, возможности которых удобнее всего демонстрировать на примере решения эталонных задач вычислительной гидромеханики, таких, как задачи течения несжимаемой вязкой жидкости в квадратной каверне с подвижной верхней крышкой (например, [26]) или в плоском канале с обратным уступом. Понятно, что в последующем эти технологии успешно применяются при моделировании реальных движений жидкости и теплообмена.

Поскольку для обеспечения устойчивости вычислительного алгоритма при росте значения числа Рейнольдса требуется уменьшать значение сеточного шага [20, 26, 27], то это, соответственно, приводит к бóльшей размерности систем линейных алгебраических уравнений (СЛАУ). Еще одна причина, по которой растет количество узлов сетки (размерность СЛАУ) — это выбор местоположения открытой выходной границы канала. Чем больше Re (то есть, например, при прочих равных условиях, — меньше вязкость), тем дальше необходимо ставить выходную границу канала вследствие появления вихрей далее вниз по течению. Таким образом, приходится увеличивать количество узлов сетки, даже если она в общем случае и неравномерная.

В этом смысле наиболее показательной является работа [20], в которой приведены решения задачи для ER = 2 и Re от 100 до 3000 с шагом 100. Для столь больших значений числа Рейнольдса автор был вынужден рассматривать канал, у которого длина в 160 раз превышала его высоту. При этом только в первой четверти длины канала решение в виде чередующихся пристенных вихрей представляло интерес. Остальные три четверти были необходимы для того, чтобы однонаправленное течение ближе к выходу трансформировалось в плоскопараллельный полностью развитый поток с параболическим профилем продольной компоненты скорости. Иными словами, 75% расчетной области присутствовало в исследовании для выполнения чисто технической функции — стабилизации итерационного алгоритма построения стационарного решения задачи.

Очевидно, что в этой ситуации при дальнейшем увеличении значения числа Рейнольдса необходимо принципиально менять подход к выбору местоположения открытой выходной границы расчетной области. Для этого в [28] излагается технология, согласно которой выходную границу канала можно помещать практически в произвольном месте, даже если эта граница пересекает пристенные вихри течения. При этом искажения решения имеют место лишь в узкой приграничной зоне, не превышающей 10–15% от общей длины канала. Соответственно задачу можно решать в так называемом «коротком» канале, в котором за счет существенного сокращения количества узлов по длине можно уменьшить шаг сетки как вдоль, так и поперек канала, оставаясь при этом в пределах разумного количества уравнений СЛАУ. В итоге возросшая за счет этого устойчивость итерационного алгоритма позволит находить стационарные решения задачи для значительно бóльших значений числа Re .

Исходя из вышеизложенного, цель настоящей работы заключается в том, чтобы с помощью технологии из [28] получить решения двумерных уравнений Навье–Стокса в плоском канале с обратным уступом при ER = 2 для чисел Рейнольдса от 1000 до 10000 с шагом 1000.

• 2.    Постановка задачи

  • 2.1.    Схема течения

• 2.2.    Математическая постановка

Рассматривается движение несжимаемой вязкой жидкости с постоянными характеристиками, такими как плотность р и динамический коэффициент вязкости ц . Считается, что поток двумерный и стационарный. На рисунке 1 в безразмерных координатах приведена схема течения: основная струя и сопутствующие вихри. В качестве характерной длины в задаче выбрана полная высота канала, в дальнейшем обозначаемая как H . Здесь l_c и h_c — соответственно безразмерные длина и высота уступа, L — безразмерная длина канала, ( 1 - h c ) — безразмерная высота входного участка канала. По определению ER = 1[ ( 1 - h c ) . Обозначения В1, В2, ..., В6 для границ расчетной области взяты из [29].

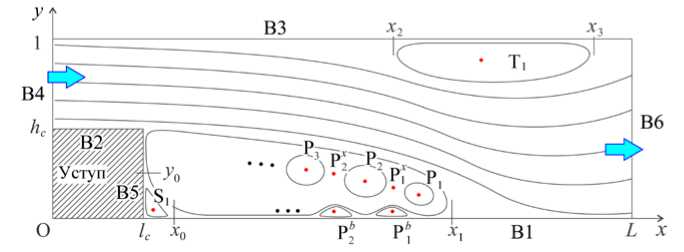
Рис. 1. Схема движения жидкости в плоском канале с обратным уступом

Полностью развитый поток (параболический профиль продольной компоненты скорости и нулевое значение поперечной компоненты скорости) втекает через левую границу В4, а через правую границу В6 жидкость вытекает (хотя частично может и втекать). При этом в силу малой длины канала течение на выходе не может считаться полностью развитым. Наряду с первичным вихрем длиной x 1 - l c непосредственно за уступом существует вторичный вихрь с центром вращения T 1 и длиной x 3 - x ₂ около верхней стенки. Также наблюдается малый вихрь длиной x 0 - l c и высотой у 0 между основанием уступа и первичным вихрем. Его центр вращения обозначен как S 1 . При Re >  1000 около нижней стенки под первичным вихрем присутствует несколько малых вихрей, которые обозначены как P i b ( i = 1, 2,... ) . Также для больших чисел Re внутри первичного вихря имеют место центры вращения: P i ( i = 1, 2,... ) . Понятно, что между ними должны существовать седловые точки течения: P i x ( i = 1, 2,... ) . Похожую схему динамики жидкости можно обнаружить в [12, 20, 28, 30]. Однако не во всех этих исследованиях явным образом обозначены множественные центры вращения и седловые точки.

Движение жидкости описывается системой нестационарных двумерных уравнений Навье–Стокса:

ди д v  „

— + — = 0

д x д у

ди ди ди — + и— + v— д t дx ду д v д v д v — + и — + v— д t дx ду

д p 1 ( д ² и д¹ и — ⁺ ~1 2+ ⁺ ^”2 д x Re ( д x ² д у

д p   1 ( д ² v д ² v

+1     2 +2

д у Re (д x ² д у ²

Здесь: u и v — горизонтальная и вертикальная компоненты скорости соответственно; p — давление; Re — число Рейнольдса Re — р U a H X , где U a — среднемассовая скорость потока на входе в канал. Время и давление обезразмерены на комплексы H/U a и р U„² соответственно. Нестационарная форма записи уравнений (2) и (3) обусловлена использованием метода установления при построении стационарного решения задачи.

Считается, что в начальный момент времени жидкость покоится: и — v = 0. Затем на левой границе В4 интенсивность течения плавно нарастает до максимального значения по закону

^и ( t , у ) = ⁶ f ( t )( у - h c )( 1 - у ) / ( 1 - h c )\ v = 0,

где

f ( t )=

0,5 { sin [ 0,5 л ( 2 t/t m - 1 ) ] + 1 } ,

1,

⁰ ^ t ^ t m , t m <  t .

На стенках канала (границы В1, В2, В3, В5) используются условия прилипания и непротекания. На выходе из канала В6 граничное условие имеет вид:

д и _ д v д x д x

Здесь необходимо иметь в виду, что в силу отсутствия точной информации о поведении решения на открытой границе В6 условие (6) следует рассматривать как приближенное. Это означает, что в процессе итерационного построения решения задачи, исходя из требования баланса массы во всей расчетной области, значения компонент u и v на каждой итерации подвергаются малой корректировке. Подробно данная технология изложена в [28].

2.3. Характеристики течения

Для всестороннего анализа получаемых решений задачи полезно рассмотреть дополнительные характеристики потока, такие как коэффициент трения C_f и коэффициент гидростатического сопротивления потоку X [31]:

C =—^w— f  о,5р ua

X=Ap  H l 0,5 PU2,

где т w — напряжение трения на стенке, A p/1 — падение давления на единицу длины вдоль канала. Используя параметры обезразмеривания, можно записать выражение для напряжения трения

XUa (аи ) т                         , w H (дпJw

где n — безразмерная внешняя нормаль к стенке, индекс « w » означает стенку. Подстановка (8) в (7) приводит к выражению для коэффициента трения:

„ _ 2 [ du । C f —

.

Re Id n J w

Однако при анализе более удобным является так называемый модифицированный коэффициент трения [8], который определяется как

* Re

f— Cf T, и не зависит от Re . Что касается коэффициента гидродинамического сопротивления потоку, то нетрудно понять, что в безразмерном виде формула для его вычисления будет следующей:

X — ² П p (0, y ) - p ( x , y ) ] dy ,                                  ⁽¹⁰⁾

x ₀

причем для обеспечения универсальности записи (10) внутри области уступа полагается, что p ( x , y ) = 0 . Понятно, что и C * , и X являются функциями только продольной координаты x .

• 3.    Метод решения

Как известно, для несжимаемых течений уравнение неразрывности (1) напрямую никак не связано с уравнениями движения (2) и (3). Для преодоления этой трудности из уравнений (1)–(3) выводится уравнение Пуассона для давления, которое в расчетном алгоритме используется вместо уравнения неразрывности (1). В результате для решения преобразованной системы применяется метод расщепления [32]. В настоящей работе он модифицирован. Отличие от оригинала заключается в том, что задача Неймана записывается не для полного давления p , а для его поправки p' , с точностью до множителя равной разности полей давления на текущем и предыдущем слоях по времени. В предположении гладкости полей переменных искомого решения такой подход приводит к условиям Неймана для p' на всех границах области независимо от выбора граничных условий для u и v .

Разностная аппроксимация исходной постановки на равномерной сетке осуществляется методом контрольного объема с первым порядком по времени и вторым по пространству [33]. Применяется неявная схема, что позволяет выбирать числа Куранта много больше единицы. Решение считается установившимся при выполнении условия:

un

-

u ” ¹

+ v

-

v

Здесь: т — шаг по времени;

τ V ⁿ _I

I

<8 .

V ⁿ — вектор скорости течения, V ⁿ | = ^( u ⁿ ) + ( v ⁿ ) , где u ⁿ

и v ⁿ

числовые векторы компонент скорости на n -м слое по времени. Во всех расчетах точность полагается равной 8 — 10 ^{- 5} , что обеспечивает стабилизацию значений компонент скорости до шестого знака

включительно после запятой. Шаг по времени вычисляется из соотношения т — Cmin ( h , Re h ² ) ,

где h — шаг по пространству, C — число Куранта, которое принимается равным 30.

Системы разностных уравнений решаются неявным итерационным полинейным рекуррентным методом второго порядка, ускоренным в подпространствах Крылова [34]. Решение СЛАУ считается найденным, если относительное уменьшение первой нормы невязки становится менее 10-8.

При выполнении этого условия первая норма разности двух следующих друг за другом векторов приближения решения не превышает 10-7.

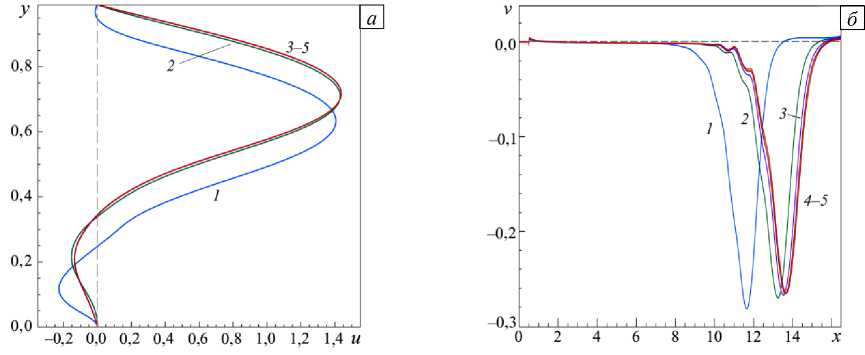
x = 10 ( а ) и поперечной v при у = 0,5 ( б ), вычисленные

Рис. 2. Профили компонент скорости – продольной u при при различных сеточных разбиениях: 1 – 2001×101; 2 – 4001×201; 3 – 6001×301; 4 – 8001×401, 5 - 10001×501

подобной задачи на многопроцессорной ЭВМ на очень подробной сетке при использовании минимального количества процессоров (для минимизации операций обмена) на каждый из процессоров приходилось порядка 1,8 млн ячеек. Такое совпадение говорит о выборе оптимального сеточного разрешения при применении современных вычислительных мощностей. Следует заметить, что столь высокие требования к степени подробности сетки обусловлены высоким значением Re . И наоборот, авторы данной работы ранее приходили к вполне удовлетворительным результатам на сеточных шагах 1/200 и даже 1/100 для малых и умеренных чисел Рейнольдса (то есть для Re < 1000), которые хорошо совпадали с литературными данными [28].

Таблица 1. Длина первичного вихря за уступом и экстремумы дополнительных характеристик потока в зависимости от сеточного разбиения расчетной области

Характеристика потока	Сеточный шаг	1/100	1/200	1/300	1/400	1/500
Длина первичного вихря за уступом x - lc	значение	10,38	13,48	13,80	13,91	13,96
*	значение	26,03	20,53	18,91	18,26	17,96
шал { с f } на В1	x -координата	12,85	14,68	15,04	15,17	15,24
*	значение	–1,384	–1,154	–1,104	–1,084	–1,074
min { C f } на вз	x -координата	10,57	12,30	12,63	12,75	12,80
min 1	значение	–0,01368	–0,01075	–0,01016	–0,00994	–0,00984
min s ^ I	x -координата	12,26	13,95	14,27	14,38	14,43

Анализ содержимого таблицы 1 говорит о том, что, начиная уже с шага 1/200, значения экстремумов характеристик потока и координаты их положения различаются слабо. Тем не менее выбор в пользу сеточного разбиения с шагом 1/300 является более предпочтительным хотя бы потому, что результаты, соответствующие этой сетке, обладают определенным «запасом прочности» в части своей количественной достоверности. При этом нетрудно видеть, что относительные отличия в значениях характеристик потока, полученных при шагах 1/300—1/500, составляют 3-5%, а по координатам и того меньше — не более 1,5%.

Для валидации программного кода были проведены сравнения вычисленных данных с теоретическими и экспериментальными данными других авторов. Соответствующие графики представлены на рисунке 3. Частичное отличие решений из [1, 23] на рисунке 3 б объясняется отсутствием в этих исследованиях начального участка канала. Степень влияния наличия начального участка на результат обсуждается в [16, 20, 26, 28].

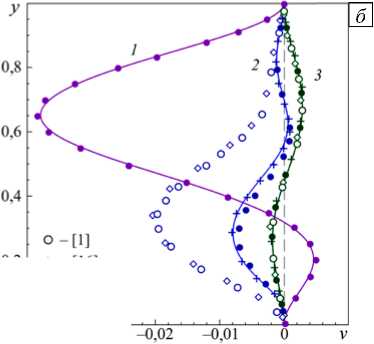
На рисунке 4 для сравнения представлены профили модифицированного коэффициента трения на верхней и нижней стенках канала. Здесь, в отличие от предыдущего рисунка, отсутствие входного участка канала не сказывается на результатах. И в том, и в другом случаях имеет место хорошее совпадение с литературными данными. На рисунке 5 показаны зависимости длины первичного вихря за уступом при ER = 2 от числа Рейнольдса в диапазоне значений от 100 до 1500. Видно неплохое согласование как теоретических, так и экспериментальных данных практически из всех работ для Re <  500. Для больших значений числа Рейнольдса заметно расхождение кривых, особенно по отношению к полученным экспериментально. В последнем случае это объясняется присутствием в экспериментах эффектов трехмерности и турбулентности [15, 17, 19].

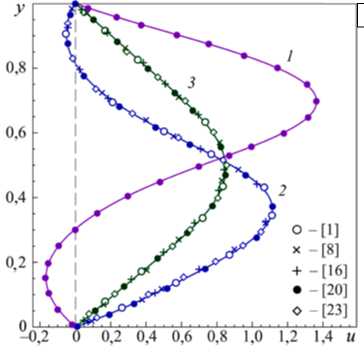
Рис. 3. Профили компонент скорости: продольной u ( а ) и поперечной v ( б ), вычисленные для Re = 800 в сечениях x : 3,5 (кривая 1 ); 7,5 ( 2 ); 12,5 ( 3 ); сплошные линии – авторские результаты

0,2 I- + -[16]

О

• " [20] О -[23]

-0^03

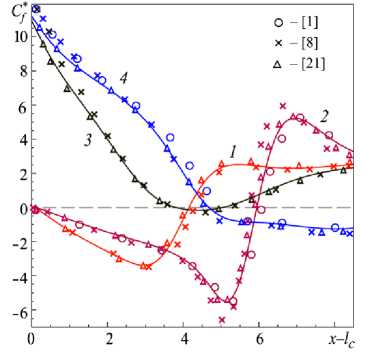
Рис. 4. Поведение модифицированного коэффициента трения на нижней и верхней стенках канала: Re = 400 , y = 0 (кривая 1 ); Re = 800 , y = 0 ( 2 ); Re = 400 , y = 1 ( 3 ); Re = 800 , y = 1 ( 4 ); сплошные линии – авторские результаты

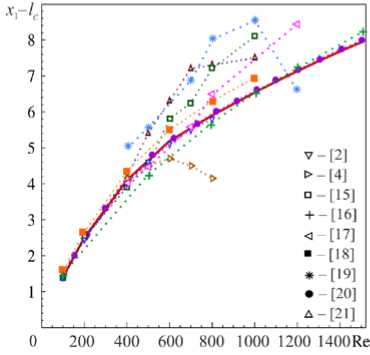
Рис. 5. Зависимости длины первичного вихря за уступом от числа Рейнольдса при ER = 2 ; сплошная линия – авторский результат

Основная цель настоящего исследования — получение решений задачи течения несжимаемой жидкости в плоском канале с обратным уступом для чисел Рейнольдса, намного превосходящих те, которые встречаются в литературных источниках. Исходя из этого, полезно провести сравнение с существующими литературными данными, отвечающими максимально большим значениям Re . Наиболее подходящей в этом смысле является публикация [20], поскольку в ней приведены детализированные характеристики потока для Re вплоть до 3000 при ER = 2 . На рисунке 6 представлены рассчитанные профили продольной компоненты скорости в различных сечениях канала для Re = 3000 , ER = 2 и для сравнения — результаты из [20].

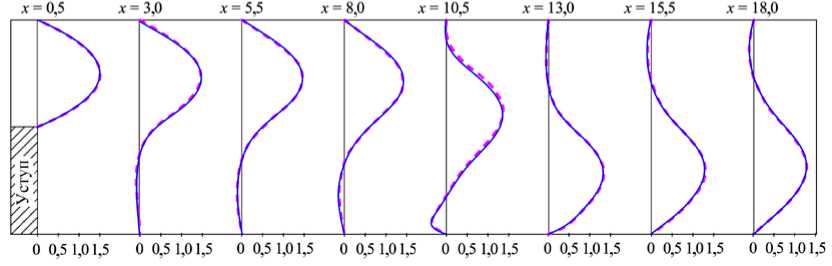
Рис. 6. Профили компоненты скорости u для Re = 3000 и ER = 2 в различных сечениях по длине канала; сплошные линии – авторский результат, штриховые линии – [20]

• 5.    Результаты расчетов и обсуждение

  Эволюция картины течения для различных значений числа Рейнольдса от 1000 до 10000 с шагом 1000 представлена на рисунке 7. Видно, что первичная зона рециркуляции удлиняется вместе с увеличением значения Re . Вторичный вихрь около верхней стенки аналогично становится длиннее, а также сдвигается вниз по потоку, «зависая» своей передней кромкой над задней кромкой первичного вихря. Необходимо отметить, что для Re >  2000 ширина основного потока практически неизменна во всей области рассмотрения. Это происходит потому, что из-за низкой, при прочих равных условиях, вязкости жидкости поток почти не тормозится и, следовательно, не расширяется. И наоборот, из-за чередования по потоку нижнего и верхнего вихрей их поперечные размеры практически совпадают. Также нетрудно увидеть, что с ростом значения Re происходит увеличение размеров малого вихря S₁ у основания уступа.

Рис. 7. Картина течения в зависимости от числа Рейнольдса Re : 1000 ( а ); 2000 ( б ); 3000 ( в ); 4000 ( г ); 5000 ( д ); 6000 ( е );

7000 ( ж ); 8000 ( з ); 9000 ( и ); 10000 ( к )

Однако наибольший интерес представляет трансформация сложной структуры зоны первичной рециркуляции за уступом. Только для Re = 1000 эта зона имеет один центр вращения. Начиная с Re = 2000 количество центров вращения, обозначенных на рисунке 1 как Р 1 , Р₂ и далее, непрерывно растет. Любопытно, что для промежутка значений Re от 1000 до 5000 их количество равно числу Рейнольдса, деленному на 1000. Но для Re >  5000 эта закономерность уже не выполняется.

Как отмечалось ранее, между внутренними центрами вращения первичного вихря P i ( i = 1,2,... ) располагаются седловые точки Р ' ( i = 1, 2,... ) . И еще одной особенностью структуры течения при больших числах Рейнольдса является возникновение малых вихрей вдоль нижней стенки, которые на рисунке 1 обозначены как Р b ( i = 1,2,... ) . При этом понятно, что их количество будет определяться количеством центров вращения P _i поскольку по длине канала каждый вихрь P _i ^b находится между вихрями P _i и Р + 1 ( i = 1, 2,... ) .

В таблице 2 для чисел Рейнольдса 5000 и 10000 приведены характеристики особых точек течения, таких как координаты центров вращения и экстремумы функций тока v и завихренности ю . Из этих данных следует, что вертикальные координаты центров вихрей слабо зависят от Re , в то время как их горизонтальные координаты чувствительны к изменению его величины. Интересная закономерность наблюдается для экстремумов функции тока и завихренности. Для средних и больших вихрей P i ( i = 1,2,... ) значения функции тока и завихренности в их центрах вращения почти не зависят от Re. Этот же вывод можно сделать и для седловых точек P i' ( i = 1,2,... ) . И наоборот, значения экстремумов малых пристенных вихрей P b ( i = 1,2,... ) изменяются в несколько раз при увеличении числа Рейнольдса от 5000 до 10000.

На рисунке 8 изображены профили горизонтальной компоненты скорости u ( у ) в сечении % = 15,5. Видно, что для Re = 1000 кривая 1 (Рис. 8 а ) качественно отличается от остальных за счет

Таблица 2. Параметры особых точек потока для больших чисел Рейнольдса

Вихрь	Re = 5000				Re = 10000
	% - l c	y	v	ю	% - l c	y	v	ю
S 1	0,088	0,082	6,08 х 10 - 6	6,65 х 10 - 3	0,145	0,115	1,63 х 10 - 5	9,55 х 10 - 3
P 1	12,512	0,185	- 4,11 х 10 - 2	–3,814	17,348	0,148	- 3,55 х 10 - 2	–5,074
P 2	11,655	0,248	- 4,19 х 10 - 2	–2,533	16,623	0,208	- 3,96 х 10 - 2	–3,075
P 3	10,748	0,295	- 3,61 х 10 - 2	–2,118	15,752	0,255	- 3,94 х 10 - 2	–2,159
P 4	9,918	0,335	- 2,98 х 10 - 2	–2,089	14,798	0,299	- 3,45 х 10 - 2	–1,844
P 5	9,228	0,348	- 2,74 х 10 - 2	–1,891	13,927	0,345	- 2,71 х 10 - 2	–2,082
P 6	–	–	–	–	13,185	0,358	- 2,44 х 10 - 2	–1,947
P 7	–	–	–	–	12,492	0,365	- 2,30 х 10 - 2	–1,735
P 1 b	12,052	0,058	1,07 х 10 - 3	1,781	16,932	0,045	1,91 х 10 - 3	4,254
P 2 b	11,142	0,065	5,69 хЮ- 4	0,801	16,102	0,062	1,74 х 10 - 3	2,013
P 3 b	10,265	0,028	2,48 х 10 - 5	0,205	15,148	0,075	1,14 х 10 - 3	1,042
P 4 b	–	–	–	–	14,192	0,078	4,81 х 10 - 4	0,473
P 5 b	–	–	–	–	13,493	0,062	2,01 х 10 - 4	0,312
P 1 x	12,115	0,258	- 2,76 х 10 - 2	–2,993	17,025	0,215	- 2,21 х 10 - 2	–3,426
P 2 x	11,222	0,325	- 2,70 х 10 - 2	–2,240	16,238	0,298	- 2,21 х 10 - 2	–2,436
P 3 x	10,310	0,348	- 2,69 х 10 - 2	–2,060	15,307	0,348	- 2,26 х 10 - 2	–1,977
P 4 x	9,358	0,348	- 2,73 х 10 - 2	–1,898	14,365	0,372	- 2,21 х 10 - 2	–1,939
P 5 x	–	–	–	–	13,548	0,372	- 2,29 х 10 - 2	–1,995
P 6 x	–	–	–	–	12,628	0,365	- 2,30 х 10 - 2	–1,754

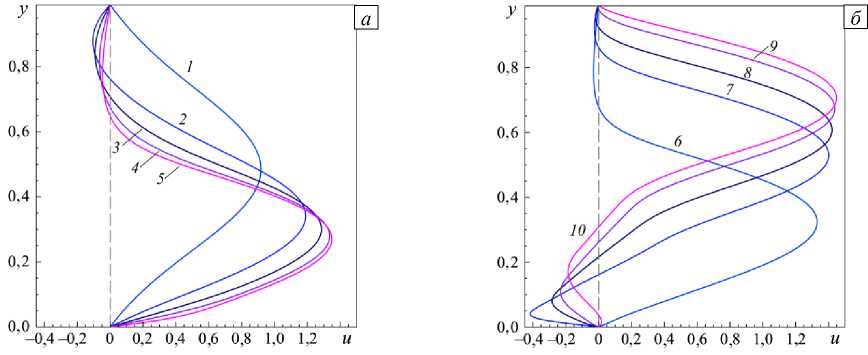
Рис. 8. Горизонтальная компонента скорости в сечении x = 15,5 при числах Рейнольдса 1000 <  Re <  5000 ( а ) и 6000 <  Re <  10000 ( б ); 1000 (кривая 1 ); 2000 ( 2 ); 3000 ( 3 ); 4000 ( 4 ); 5000 ( 5 ); 6000 ( 6 ); 7000 ( 7 ; 8000 (8); 9000 ( 9 ); 10000 ( 10 )

однонаправленности движения жидкости в этом сечении — обе зоны рециркуляции находятся вверх по потоку, в то время как для остальных чисел Рейнольдса имеют место участки с отрицательной скоростью, то есть присутствуют вихревые зоны. Причем, если для кривых 2 – 6 участки отрицательных u ( y ) наблюдаются у верхней границы, что говорит о наличии верхнего вихря (см. Рис. 7 б – е ), то у кривых 7–10 верхний участок отрицательных значений горизонтальной компоненты скорости либо исчезающе мал, либо отсутствует. Зато у этих кривых появляется нижний участок отрицательных значений u ( у ), то есть координата правой кромки первичного вихря за уступом для чисел Re >  7000 превышает величину 15,5 (см. Рис. 7 ж – к ). Относительно малые по модулю скорости возвратного течения свидетельствуют о слабой по отношению к основному потоку интенсивности движения жидкости в вихрях. Также следует отметить незначительную зависимость максимума скорости от величины Re , что естественно при практически неизменной ширине основного однонаправленного тока жидкости.

Профили вертикальной компоненты скорости v ( y ) в том же сечении представлены на рисунке 9. Видно, что максимумы абсолютных значений v для 1000 <  Re <  5000 (Рис. 9 а ) на порядок меньше подобных значений для Re >  5000 (Рис. 9 б ). Следовательно, графики рисунка 9 а соответствуют практически плоскопараллельному течению жидкости в рассматриваемом сечении для Re <  5000 как в основном потоке, так и в верхнем вихре, а графики рисунка 9 б — интенсивному нисходящему потоку ( v отрицательна) над задней кромкой первичного вихря. При этом постепенное уменьшение максимума модуля v при Re от 7000 до 10000 говорит о восстановлении в основном потоке режима почти плоскопараллельного течения при у >  0,5 (см. Рис. 7 е-к ).

На рисунке 10 смена завихренностью ю знака вблизи стенок отражает перемену направления движения жидкости около стенок в рассматриваемом сечении с ростом величины числа Рейнольдса, что хорошо видно при сравнении фрагментов ( е ) и ( ж ) рисунка 7. При этом амплитуда изменения завихренности у нижней

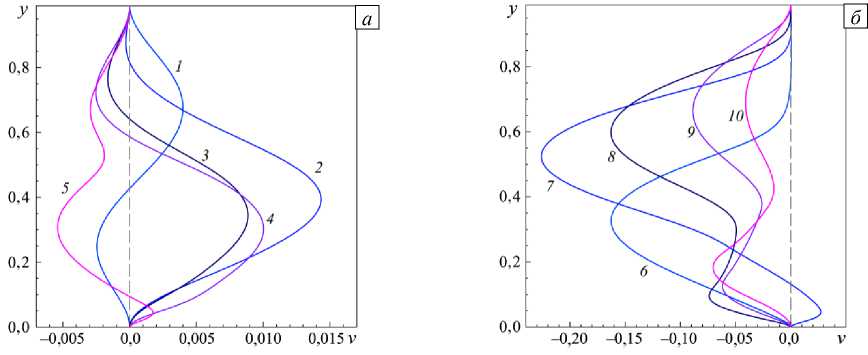
Рис. 9. Вертикальная компонента скорости в сечении x = 15,5 при числах Рейнольдса 1000 <  Re <  5000 ( а ) и 6000 <  Re <  10000 ( б ); 1000 (кривая 1 ); 2000 ( 2 ); 3000 ( 3 ); 4000 ( 4 ); 5000 ( 5 ); 6000 ( 6 ); 7000 ( 7 ); 8000 (8); 9000 ( 9 ); 10000 ( 10 )

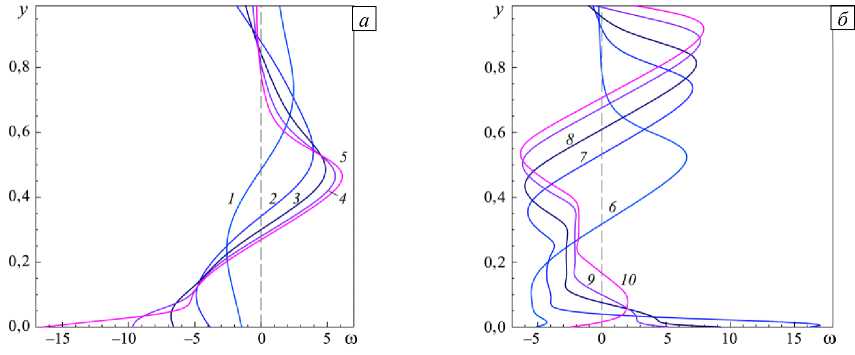
Рис. 10. Завихренность в сечении x = 15,5 при числах Рейнольдса 1000 <  Re <  5000 ( а ) и 6000 <  Re <  10000 ( б );

1000 (кривая 1 ); 2000 ( 2 ); 3000 ( 3 ); 4000 ( 4 ); 5000 ( 5 ); 6000 ( 6 ); 7000 ( 7 ); 8000 (8); 9000 ( 9 ); 10000 ( 10 )

стенки намного превышает аналогичную величину у верхней стенки, что также свидетельствует о малой интенсивности течения в зоне верхнего вихря. Более того, для Re = 4000 + 6000 в диапазоне высот 0,7 <  у <  1,0 величина ю почти нулевая. То есть в этом случае имеет место практически безвихревая циркуляция жидкости вокруг центра T₁ верхнего вихря. Иными словами, здесь жидкость вращается почти как твердое тело, аналогично тому, как это происходит в первичном вихре задачи стационарного течения в плоской каверне с подвижной верхней крышкой (см., например, [26]).

И наконец, на рисунке 11 приведено поперечное распределение функции тока v ( У )• Из графиков следует, что поток в рассматриваемом сечении ускоряется, о чем свидетельствует уменьшение наклона кривых к оси абсцисс с ростом значения Re. Для Re >  6000 присутствие первичной зоны рециркуляции приводит к изменению знака v в нижней части профиля. При этом хорошо видно, что рост значения числа Рейнольдса вызывает увеличение высоты первичного вихря, которая достигает своего максимума приблизительно равного 0,5 для Re = 10000.

Совокупный анализ кривых на рисунках 8-11 говорит о том, что при переходе от Re = 6000 к 7000 (то есть от кривой 6 к кривой 7 ) происходит качественное изменение структуры течения в сечении x = 15,5 . Это связано с появлением в данном сечении задней кромки первичного вихря за уступом. Некоторое исключение представляют собой графики на рисунке 9, которые свидетельствуют о перестроении движения жидкости между кривыми 5 и 7 . Первую стадия его видоизменения — между профилями 5 и 6 — можно объяснить появлением нисходящего основного течения (см. Рис. 7 е ), а причина второй стадии перестройки потока — между кривыми 6 и 7 — все та же — появление задней кромки первичного вихря.

Поведение завихренности вдоль продольных стенок канала представлено на рисунке 12. Из-за наличия малых вихрей P b ( i = 1 , 2 , ...) профили ю вдоль нижней стенки характеризуются ярко выраженной немонотонностью. При этом границы пристенных вихрей несложно установить в силу того,

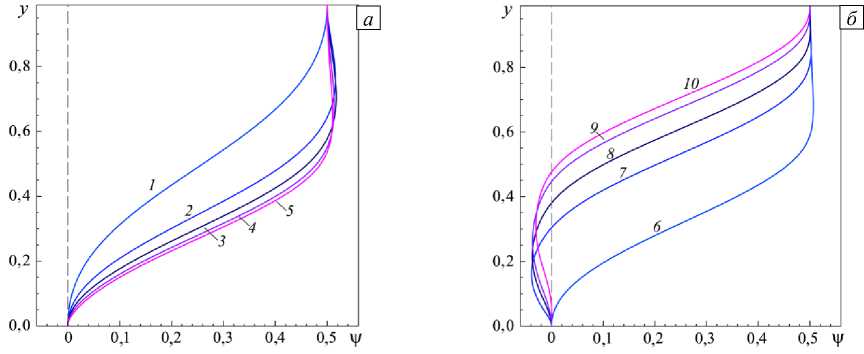
Рис. 11. Функция тока в сечении x = 15,5 x = 15,5 при числах Рейнольдса 1000 <  Re <  5000 ( а ) и 6000 <  Re <  10000 ( б ); 1000 (кривая 1 ); 2000 ( 2 ); 3000 ( 3 ); 4000 ( 4 ); 5000 ( 5 ); 6000 ( 6 ); 7000 ( 7 ); 8000 (8); 9000 ( 9 ); 10000 ( 10 )

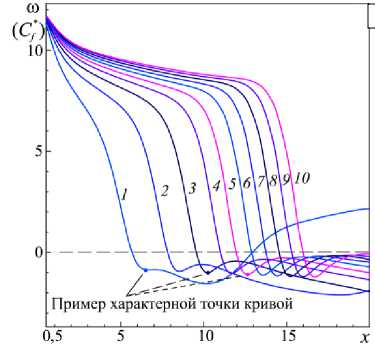
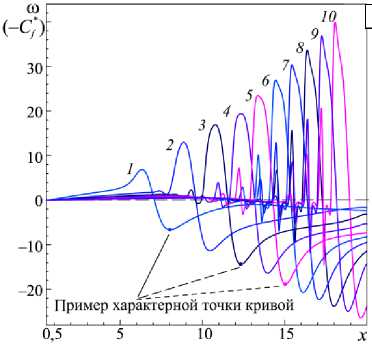
Рис. 12. Распределение завихренности (модифицированного коэффициента трения) вдоль стенок канала в сечениях у = 1 ( а ) и у = 0 ( б ) при различных значениях числа Рейнольдса Re : 1000 (кривая 1 ); 2000 ( 2 ); 3000 ( 3 ); 4000 ( 4 ); 5000 ( 5 ); 6000 ( 6); 7000 ( 7 ); 8000 (8); 9000 ( 9 ); 10000 ( 10 )

б

что при переходе от одного вихря к другому завихренность меняет свой знак. По причине совпадения на стенке определений завихренности и модифицированного коэффициента трения (см. формулу (9)) кривые на рисунке 12 можно рассматривать как распределение C^* _f по длине канала. Единственное отличие этих двух величин заключается в противоположности их знаков на нижней стенке ( C * = - ю при у = 0) из-за внешнего направления нормали, используемой в формуле для C f .

Графики коэффициента гидродинамического

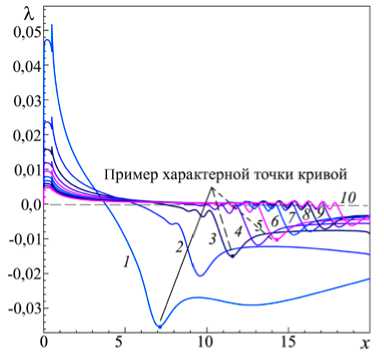
Рис. 13. Распределение коэффициента гидродинамического сопротивления потоку при различных значениях числа Рейнольдса Re : 1000 (кривая 1 ); 2000 ( 2 ); 3000 ( 3 ); 4000 ( 4 ); 5000 ( 5 ); 6000 ( 6 ); 7000 ( 7 ); 8000 (8); 9000 ( 9 ); 10000 ( 10 )

сопротивления потоку вдоль канала приведены на рисунке 13. Здесь нужно обратить внимание на следующие моменты. Во-первых, значение X во входной части канала (0 < x < lc) почти постоянно и хорошо согласуется с величиной, получаемой по известной формуле для гладких плоских каналов: X = 24/Rec [31], где Re c определяется через (1 - hc) — высоту входной части канала. Во-вторых, скачок X в сечении x0 - lc   говорит о сингулярности решения в окрестности верхней кромки уступа. В-третьих, положение локального минимума профиля X зависит от расположения задней кромки первичного вихря, в то время как местонахождение передней кромки верхнего вихря T1 никак на это положение не влияет.

И наконец, в-четвертых, слабые колебания кривых около нулевого уровня указывают на сложную структуру течения в задней по потоку части первичной зоны рециркуляции.

Все графики на рисунках 12 и 13 обладают интересной особенностью: позиция характерной точки кривой (такой точкой, например, может быть локальный экстремум) описывается приближенной формулой

x — l

c

~ ⁽ x 0 ^- l c )

Re

Re 0

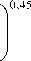
где Re₀ есть некоторое фиксированное число Рейнольдса, а x ₀ — горизонтальная координата рассматриваемой характерной точки кривой при Re = Re₀ (см. Рис. 12 и 13). При этом следует заметить, что при различных Re графики не являются подобными. Для этого достаточно обратить внимание на отличия в поведении кривых ю и X для Re = 1000 от их поведения для других значений Re или сравнить количество локальных экстремумов у профилей X для различных чисел Рейнольдса. Данные в таблице 3 иллюстрируют точность соотношения (12) на примере позиций локального минимума кривых

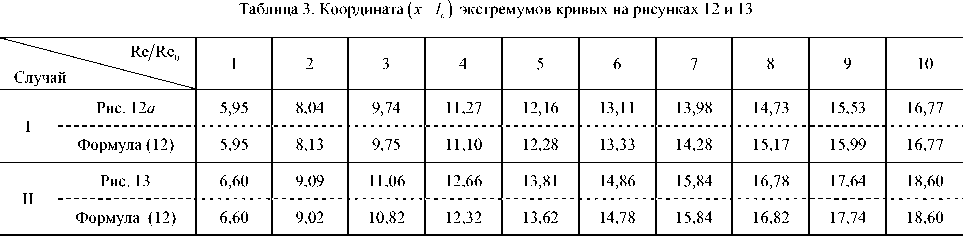
завихренности при у = 1 (Рис. 12 а ) и локального минимума кривых коэффициента X (Рис. 13) (в таблице они обозначены как случай I и II соответственно). Если принять Re₀ = 1000, то по рисункам 12

и 13 также нетрудно установить, что x ₀ - 1 с составляет 5,95 для случая I и 6,60 для случая II.

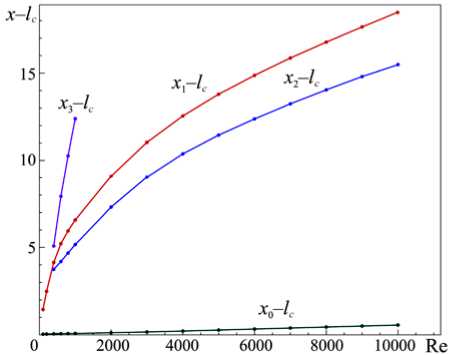
Рис. 14. Зависимости от числа Re положений передних и задних кромок вихрей; здесь x ₀ - l c и x - l c - горизонтальный размер, соответственно, вихря в основании уступа и первичного вихря за уступом, x ₂ - l c и x 3 - l c -горизонтальное расстояние от уступа до передней и задней кромок верхнего вихря (см. Рис. 1)

Видно хорошее согласование расчетных и аппроксимационных результатов: относительная ошибка не превышает 2–3%. Понятно, что формула (12) справедлива только для ER = 2 . Если же возникнет необходимость в дополнительном учете величины ER , то это приведет к более сложному соотношению, подобному, например, формуле определения длины первичного вихря в [21].

На рисунке 14 изображены зависимости положений передних и задних кромок вихрей для Re от 100 до 10000 в пределах горизонтального размера расчетной области. Малая длина кривой x ₃ - l c объясняется, с одной стороны, быстрым увеличением координаты x ₃ , а с другой стороны, небольшим размером самого канала. Нетрудно видеть, что координаты кромок вихрей зависят от Re нелинейно. Однако с ростом значения числа Рейнольдса эта нелинейность становится пренебрежимо малой.

• 6.    Заключение

  В работе представлены численные решения уравнений Навье–Стокса применительно к задаче стационарного течения несжимаемой вязкой жидкости в коротком плоском канале с обратным уступом. Полученные результаты хорошо согласуются как с теоретическими, так и экспериментальными данными других исследователей. Продемонстрирована эволюция течения при параметре расширения потока ER = 2 для чисел Рейнольдса от 1000 до 10000 с шагом 1000. Определены основные параметры центров вихрей: координаты, значения функций тока и завихренности. Проанализированы профили компонент скорости, функции тока и завихренности в поперечном сечении х = 15,5, а также коэффициентов трения и гидродинамического сопротивления потоку вдоль канала. Приведена простая аппроксимационная формула для нахождения положений характерных точек кривых C * и X .

На базе полученных решений задачи для чисел Рейнольдса от 1000 до 10000 при ER = 2 можно сделать следующие выводы:

• 1.    С ростом величины числа Рейнольдса структура течения усложняется вплоть до формирования сильно растянутого по потоку первичного вихря за уступом с несколькими центрами вращения и седловыми точками между ними.

• 2.    Между первичным вихрем и нижней стенкой возникают небольшие вихри, количество которых растет по мере увеличения значения Re .

• 3.    Распределение по длине канала модифицированного коэффициента трения и гидродинамического сопротивления потоку имеет немонотонный характер, что отражает сложную структуру отрывного течения в канале.

• 4.    Максимальная абсолютная величина модифицированного коэффициента трения достигается при максимальном значении Re . И, наоборот, максимальная абсолютная величина коэффициента гидродинамического сопротивления потоку имеет место при минимальном значении числа Рейнольдса.