В трещиновато-пористых и разломных зонах земной коры широко распространены процессы, включающие гидротермальную конвекцию. С нею связана проблема правильной интерпретации аномалий теплового потока. Так, над центральной частью нефтяных и газовых месторождений образуются положительные аномалии, и отрицательные по краям контура, охватывающего месторождение [1]. В работе [2] высказано предположение, что конвективные потоки в умеренно проницаемых пластах– коллекторах, вызванные естественным температурным градиентом, могут обеспечить механизм миграции углеводородов из нефтематеринских толщ в области нефтескопления. Одной из наиболее вероятных причин вариаций значений теплового потока в зонах срединно-океанических хребтов принято считать наличие на их склонах гидротермальной конвекции [3]. Анализ условий возникновения термоконвективных течений в осадочном чехле показывает [4], что при имеющихся оценках значений физических параметров наличие конвекции здесь скорее правило, чем исключение. В работах, посвящённых теоретическому и экспериментальному анализу условий возникновения тепловой конвекции [5–12], обычно рассматривается горизонтальный или наклонный флюидонасыщенный слой с заданными значениями температуры на границах. В работе [9] показано, что в наклонном слое с фиксированными границами неустойчивость возникает при числе Рэлея-Дарси Rd > 4n2/cos а, где а является углом наклона слоя к горизонтальной плоскости; с увеличением угла наклона устойчивость повышается.

Условия возникновения конвекции в разломах и коллекторах требуют рассмотрения задачи с неоднородными по проницаемости массивами. Так, в работе [13] обсуждается проблема развития свободной конвекции в зоне вертикального разлома в массиве малопроницаемых пород при постоянных температурах на горизонтальных границах. На примере высокопроницаемого вертикального разлома, помещённого в непроницаемый теплопроводный куб, в [14] посредством численного моделирования исследовалась гидротермальная конвекция. В работах [15, 16] изучались 3D модели применительно к горизонтальному слою пористой среды, насыщенной флюидом, при различных числах Рэлея–Дарси. Получено, что в зависимости от значения числа Рэлея–Дарси реализуются различные пространственные структуры и тепловые потоки. В [13–16] принято, что теплофизические свойства пород, такие как плотность, температуропроводность, пористость и другие, постоянны во всей области моделирования. Условия возникновения конвекции в горизонтальном пористом слое, ограниченном сверху и снизу бесконечными однородными массивами с разной теплопроводностью, анализировались в [17].

В настоящей работе проводится численное исследование условий возникновения свободной тепловой конвекции в наклонном пористом проницаемом слое, насыщенном однокомпонентной вязкой жидкостью, помещённом в малопроницаемый массив, при различных углах наклона к горизонтальной поверхности. Рассматривается модель, в которой область слоя имеет более высокую проницаемость, чем окружающий массив. Таким образом, течение жидкости в окружающем массиве существенно затруднено. Впервые подобная модель применялась в работе [18], где использовалась однородная пространственная сетка и получены решения только для трёх пространственных ориентаций слоя (горизонтального, вертикального и с углом наклона а = 45 ° ). В настоящей работе на расчётную область наносится неравномерная пространственная прямоугольная сетка, что позволяет рассмотреть конвекцию при большем разнообразии значений угла наклона пористого слоя, в котором реализуется тепловая конвекция.

2.    Модель и уравнения

Уравнения, описывающее медленное конвективное движение вязкой несжимаемой однокомпонентной жидкости в пористой среде, имеют вид [7, 19]:

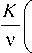
• -— + g в T e _z ρ₀

  (р c_p ) c d T + (p c_p ) f u -V T = X c V ² T ,                                   (1)

  d t

  V- u = 0 .

  Здесь: u = n- v — скорость Дарси фильтрации флюида в пористой среде, где п — пористость среды, v — средняя скорость частиц флюида в порах; p — давление; ρ₀ — равновесная плотность флюида; g — ускорение свободного падения; в — коэффициент теплового расширения флюида; v — кинематическая вязкость флюида; К — проницаемость среды; T — температура; e z — единичный вектор; X_c — теплопроводность среды; ( р c p ) _c — теплоёмкость насыщенной жидкостью среды, ( р c_p ) f — теплоёмкость жидкости; V — векторный дифференциальный оператор.

  Примем в качестве единиц: для длины — толщину проницаемого слоя H ; для скорости фильтрации — к ef [H , где к ef = X с Др c_p ) f — эффективный коэффициент температуропроводности среды; для времени — bH ²/к ef , где b = ( р c_p ) _c Др c_p ) f — отношение теплоёмкостей среды и флюида; для давления — P ₀ vк ef /К . Тогда система безразмерных уравнений свободной тепловой конвекции в проницаемой пористой среде будет иметь вид:

  u = -V p + Rd O e _z

  — + u -V O = V² O d t

  V- u = 0,

  
  

  ^,

  
  

  ^,

  
  
  
  
  
  
  
  
  
  

где 9 = ( T - T ₀)/ A T H — безразмерная температура, T ₀ — температура на верхней холодной границе слоя,

∆ T_H — вертикальная разница температур в слое мощностью H . Безразмерная температура θ изменятся от θ ₀ = 0 (на верхней границе) до θ ₁ = c =∆ T ∆ T_H (на нижней границе), где ∆ T — разность температур между изотермическими горизонтальными границами вмещающей области. Значение параметра c подбирается в каждом отдельном случае в зависимости от угла наклона проницаемого слоя. Интенсивность конвекции определяется числом Рэлея–Дарси:

Rd β gH ∆ T H K

Rd = νκ _ef

.

Будем считать, что во вмещающем непроницаемом массиве течение отсутствует. Соответствующее уравнение для распространения тепла в массиве запишем как

∇ ²θ. ∂ t

На боковых границах массива зададим условия отсутствия потока тепла: ∂ θ ∂ x = 0. Для проекций вектора скорости u на оси x и z , соответственно, примем: u =∂ ψ ∂ z и v =-∂ ψ ∂ x , где ψ — функция тока. При таком выборе выражения для функции тока соотношение ∇⋅ u = 0 выполняется автоматически. На границах проницаемой области функцию тока обнулим: ψ= 0 .

Применяя к уравнению (2) 1 операцию «rot » и учитывая граничные условия, запишем систему уравнений свободной тепловой конвекции во внутренней области в переменных ( ψ , θ ):

∇ ²ψ = - Rd ∂ ^θ ;

∂ x

∂ θ ∂ ψ ∂ θ ∂ ψ ∂ θ

+     -     =∇2θ.

∂t ∂z∂x ∂x∂z

Совместное решение уравнений (4) и (5) позволяет учитывать условия теплового контакта между двумя областями.

3. Численный метод

Для численного исследования свободной конвекции в наклонном слое, помещённом в непроницаемый массив, используются неравномерная прямоугольная сетка и метод конечных разностей. Изменением соотношения размеров ячейки h_xh_z регулируется α — угол наклона проницаемого слоя к горизонтальной плоскости. Так, при равномерной пространственной сетке ( h_x = h_z ) получаем значение α= 45 ° , при h_x < h_z — α> 45 ° (Рис. 1 а ), при h_z < h_x — α< 45 ° (Рис. 1 б ). Такой подход делает возможным совместное решение уравнений (4) и (5) для обеих областей в одной системе координат. Определяющим является то, что независимо от ориентации слоя, в котором реализуется конвекция, слагаемое, описывающее силу плавучести (правый член в уравнении (5) ₁), обуславливается только горизонтальным градиентом температуры.

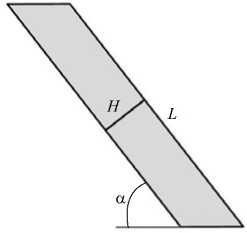
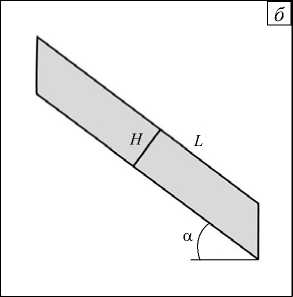
Рис. 1. Схема размещения проницаемого слоя во вмещающем непроницаемом массиве под различным углом наклона к горизонтальной плоскости: α > 45 ° ( а ); α< 45 ° ( б )

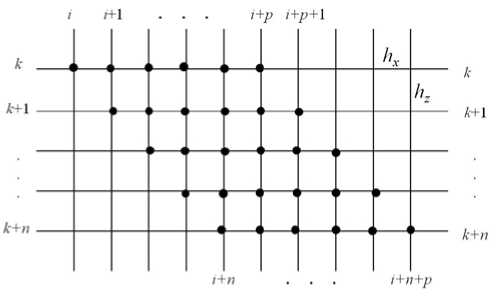
Рис. 2. Численная схема для наклонного слоя; точками выделена проницаемая область

Для решения уравнения (5) 1 использовался итерационный метод последовательной верхней релаксации [20, 21]. В зависимости от соотношения размеров прямоугольной сетки подбиралось отвечающее ей оптимальное значение параметра релаксации. На рисунке 2 точками выделена проницаемая область, что соответствует случаю, изображенному на рисунке 1 а . Внешний цикл осуществлялся по вертикальной компоненте.

На верхнем горизонтальном слое индексы вычисляемых значений компонент функции тока изменялись по координате x от i до i + p, на следующем, (k +1) -м слое — от i +1 до i + p +1; на нижнем горизонтальном слое

( k + n ) — от i + n до i + p + n . Здесь p и n —

задаваемые параметры. Параметр p для каждого угла наклона проницаемого слоя подбирался так, чтобы мощность слоя была порядка единицы, что соответствует характерному размеру слоя — его толщине H , а число n должно было давать значение аспектного отношения порядка 10.

Основные численные результаты получены для угловых точек с координатами ( i , k )

и ( i + n + p , k + n ), отстоящих от горизонтальных и вертикальных границ непроницаемого массива на расстояние порядка единицы мощности слоя. Для численного решения уравнений (4) и (5) 2 применялись метод сквозного счёта и неявная разностная схема переменных направлений [20, 21]. Минимальный пространственный шаг дискретизации на прямоугольной сетке составлял 0,02.

4.    Результаты численного моделирования

Реальные геологические среды отличаются большой неоднородностью по составу и, соответственно, по физическим свойствам. Из всех параметров, входящих в выражение для числа Рэлея–Дарси (3), наиболее вариабельным является коэффициент проницаемости K , который может меняться в очень широких пределах. Так, у разных фаций резервуарных песчаников при увеличении пористости на несколько процентов проницаемость возрастает на несколько порядков [22]. Учитывая, что другие физические характеристики геологической среды, такие как пористость, теплопроводность, температуропроводность и другие, более стабильны, в настоящей работе рассмотрен случай, когда, по аналогии с [13, 14], они принимаются одинаковыми и постоянными в обеих областях. Устойчивость качественно определяется характерным размером H и проницаемостью K . С помощью (3) можно оценить порядок величин, необходимый для реализации конвекции. Примем, согласно [14], для коэффициента объёмного расширения воды в значение 3 - 10 ^{- 3} К^-1; для эффективной температуропроводности к ef — 10 ^{- 6} м²/с; для градиента температуры A T H [И — 0,03 K/м. Тогда при И = 200 м конвекция может возникнуть при проницаемости K , равной 10 ^{- 13} м². Такой порядок значений проницаемости характерен для умеренно проницаемых пород [22]. У высокопроницаемых пород, таких как грубые песчаники, трещиноватые известняки, конвекция может реализовываться в более тонких слоях, где H составляет лишь десятки метров.

Сохранность нефтяных и газовых залежей обеспечивается плохо проницаемыми для нефти и газа породами (глинами, глинистыми сланцами и другими), подстилающими и перекрывающими породы– коллекторы. Непроницаемые породы предохраняет залежи от утечки нефти и газа. Для аккумуляции нефти и газа, находящихся в рассеянном состоянии в песчаных или трещиноватых породах, и образования их залежей должны существовать условия динамичности флюидов, а для этого необходимы благоприятные структурные формы (купола, антиклинали, синклинали, моноклинали и другие), а также тепловая конвекция как интенсивный механизм миграции флюидов в пористых средах, особенно в их наклонных слоях.

Для того чтобы выяснить границы устойчивости, система уравнений (5) решалась при различных (с точностью до 0,1) значениях числа Rd . Выделялись решения, при которых функция тока в расчётной области стремились от некоторого начального распределения к нулю и означала устойчивый режим. Ненулевое распределение отвечало неустойчивому режиму.

Для тестирования точности применяемой сетки, характеризующейся различными соотношениями горизонтальных и вертикальных размеров, был рассмотрен классический пример возникновения конвекции в бесконечном плоском слое с постоянными температурами на горизонтальных границах [5–7].

Критическое значение числа Рэлея–Дарси для этого случая составляет Rd cr = 4 п 2 и при различных размерах сетки

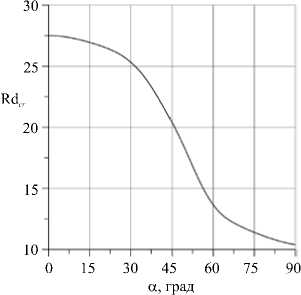
Рис. 3. Вычисленная зависимость

определяется с точностью до 0,2. В работе [17] рассматривается устойчивость горизонтального слоя, находящегося между двумя бесконечными полупространствами, отличающимися теплопроводностью. Показано, что при уменьшении теплопроводности граничных массивов устойчивость равновесия монотонно понижается, и в случае теплоизолированных границ число Rd _cr составляет порядка 12.

На рисунке 3 представлена вычисленная зависимость критического числа Rdcr от угла наклона а для проницаемого слоя.  Угловые точки слоя отстоят

от вертикальных и горизонтальных границ вмещающего критического числа Рэлея–Дарси Rdcr массива на расстояния порядка мощности слоя. Видно,                                    cr от а - угла наклона проницаемого слоя что с увеличением угла наклона устойчивость снижается.

к горизонтальной плоскости

Эти результаты можно сопоставить с аналитическими решениями для неустойчивости Рэлея–Хадли в наклонном слое, где температура линейно изменяется вдоль границы слоя [12]. Так, например, для режима «охлаждение вверх» (upward–cooling) отмечено снижение устойчивости. При больших градиентах и углах наклона функция нейтральной устойчивости зависимости числа Рэлея–Дарси Rd(k) от волнового числа k не имеет положительного минимума.

Как показано на рисунке 3, для горизонтального слоя значение Rd _cr составляет порядка 27,5.

Увеличение размеров вмещающей области приводит к некоторому уменьшению устойчивости. Когда угловые точки наклонного слоя находятся на безразмерном расстоянии 4 от вертикальных и горизонтальных границ, для горизонтального слоя получено критическое значение Rdcr ®26,8, соответствующие величины, отвечающие различным сеткам, для вертикального слоя — Rdcr = 10,4 и 10,2, а для слоя с углом наклона а = 45° — Rdcr = 20,3 и 19,9. Построение кривой устойчивости, представленной на рисунке 3, требует достаточно точного нахождения критических значений числа Рэлея–Дарси. Поэтому в данной работе для трёх рассмотренных выше примеров ориентации слоя получены более точные, по сравнению с результатами работы [18], критические значения.

Для подтверждения адекватности полученных результатов сравним их с данными авторов [8, 13, 17]. Числовые данные для горизонтального слоя находится в хорошем соответствии со значением Rd cr ® 26,5 из [17] при условии равенства теплопроводностей слоя и граничащих массивов. В работе [13] рассматривается конвекция в вертикальном проницаемом слое различной мощности, заключённом в непроницаемый куб. При отношении полуширины слоя к высоте, равном А = 0,01, тепловая конвекция начинается при условии Rd >  16,38. Вид кривой, представленной на рисунке 3, качественно совпадает с полученным в работе [8] для наклонного подогреваемого снизу слоя с изотермическими и теплоизолированными границами. Различие заключается в том, что в [8] угол наклона отсчитывается от вертикали. Понижение устойчивости с увеличением угла можно объяснить тем, что вертикальные размеры слоя в проекции на ось z увеличиваются.

На рисунке 4 показано изменение структуры тепловой конвекции в зависимости от угла наклона при небольшой закритичности. Видно, что с увеличением угла число конвективных ячеек уменьшается, а при больших углах реализуется одноячеистая структура.

Существенно меняется структура конвекции и для различных значений числа Рэлея–Дарси при одном и том же угле наклона. На рисунке 5 представлены распределения изолиний функции тока v для отношения горизонтального размера ячейки к вертикальному, равного hjh z = 2. Видно, что уже при двукратном увеличении значения Rd реализуется конвекция с одноячеистой структурой; границы между ячейками представляют собой вертикальные линии. Эти результаты качественно соответствуют примерам с изотермическими границами в случае, когда для фиксированных чисел Рэлея–Дарси в зависимости от угла меняется и структура [9].

В геотермии (геотермике) одним их главных параметров в изучении теплового поля Земли является плотность теплового потока q = -X ( dT/dz ) , где X — коэффициент теплопроводности. Источники, вызывающие аномалии локальных тепловых потоков, разнообразны: многолетнемерзлотные породы с отрицательными температурами и мощностью до сотен метров; породы и руды с повышенной радиоактивностью; экзотермические и эндотермические процессы, происходящие в нефтегазоносных горизонтах, залежах угля, сульфидных и других рудах; современный вулканизм и тектонические движения; циркуляция подземных, в том числе термальных, вод и другое. Перенос тепла за счёт свободной

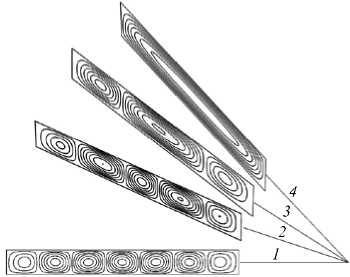
Рис. 4. Изолинии функции тока у в проницаемом слое для установившихся режимов конвекции при небольшой закритичности Rd = 1,02Rd c в зависимости от угла наклона а и соотношения, размеров расчётной прямоугольной сетки hx/h z : а = 0 ° , горизонтальный слой (кривая 1 ); а = 25,6 ° , h x/ h z = 2 ( 2 ); а = 37,6 ° , hx/h z = 1,3 ( 3 ); а = 45 ° , hjh_z = 1 ( 4 )

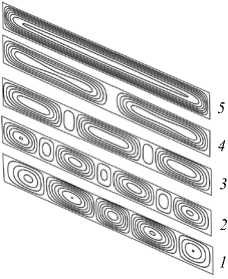
Рис. 5. Изолинии функции тока у для установившихся режимов конвекции в проницаемом слое при соотношении размеров hx/h z = 2 а = 25,6 ° и различных значениях числа Рэлея–Дарси Rd : 1,02Rd _cr (кривая 1 ); 1,15Rd _cr ( 2 ); 1,5Rd _cr ( 3 ); 1,7Rd _cr ( 4 ); 2,0Rd _cr ( 5 )

тепловой конвекции в пористой среде служит одним из механизмов образования в тепловом потоке локальных аномалий. На характеристики теплового потока влияет как интенсивность конвекции, так и глубина залегания пород ( h ), в которых он распространяется.

На рисунке 6 представлены кривые распределения q_cq_d , где q_c — плотность теплового потока при наличии конвекции, q_d — плотность потока, обусловленного кондуктивным переносом тепла, в зависимости от глубины залегания проницаемого слоя. Проницаемый слой наклонен под углом а = 45 ° . Для вмещающего непроницаемого массива приняты следующие относительные размеры: 15 (по x ) и 12 (по z ). Число Рэлея-Дарси составляет Rd = 40, что соответствует примерно двукратному превышению критического числа Rd cr для заданного а . Проницаемый слой отстоит от обеих боковых границ на расстояние 4. В рассматриваемом случае, как показано выше, реализуется конвекция одноячеистой структуры. При этом течение является восходящим вдоль верхней границы слоя и, соответственно, нисходящим вдоль нижней границы. Как следует из рисунка 6, аномалии относительной плотности теплового потока качественно определяются глубиной залегания, и это положительные аномалии, то есть ( qdq d — 1) >  0 . Для слоя с неглубоким залеганием на краях выделяются отрицательные значения — ( qdq d - 1) <  0 . С увеличением интенсивности конвекции такой характер плотности потока проявляется

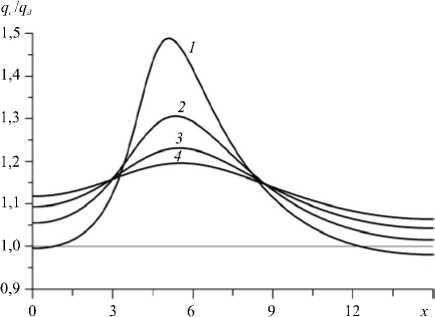
Рис. 6. Отношение плотностей теплового потока q_cq_d на поверхности непроницаемого массива в зависимости от глубины залегания верхней угловой точки проницаемого слоя h : 1 (кривая 1 ); 2 ( 2 ) ; 3 ( 3) ;4 ( 4 ); число Рэлея–Дарси Rd = 40 , угол наклона а = 45°

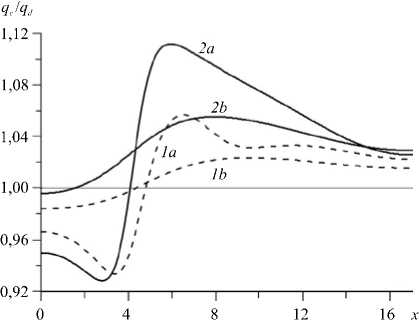
Рис. 7. Отношение плотностей теплового потока q_cq_d на поверхности непроницаемого массива при Rd = 40 (пунктирные линии), Rd = 52 (сплошные линии) и угле наклона а = 25,6 ° ; глубина залегания h = 1 (кривые 1a и 2a ) и h = 4 ( 1b и 2b )

уже и на больших глубинах. Так, для Rd = 60 отрицательные аномалии на краях прослеживаются при h = 2. Необходимо отметить следующую важную особенность: на поверхности слоя интегральное значение отношения плотностей теплового потока для разных значений числа Рэлея–Дарси не зависит от глубины залегания слоя.

Качественно иная картина распределения относительной плотности теплового потока на поверхности слоя с небольшим углом наклона и отношением hjh z = 2 представлена на рисунке 7. Размеры вмещающего массива следующие: 17 (по x ) и 10 (по z ). Для угла наклона а = 25,6 ° число Rd = 52 соответствует примерно двукратному значению критического числа Рэлея–Дарси. В данном примере прослеживается ярко выраженная асимметрия с отрицательным потоком со стороны области подстилания наклонного слоя. Для малых глубин залегания и малоинтенсивной конвекции, при которой сохраняется многоячеистая структура, выделяется несколько максимумов плотности теплового потока (кривая 1а ). Как следует из рисунков 6 и 7, угол наклона существенно влияет и на значения плотности теплового потока, наблюдаемого на поверхности. Для аномалий плотности теплового потока с большим углом наклона (см. Рис. 6) наблюдается соответствие картине, характерной для компактных областей (например для шаровой [4]), в которых реализуется конвекция.

5.    Заключение

Проведено численное исследование конвективной устойчивости пористого слоя, помещённого в непроницаемый массив под различным углом наклона к горизонтальной плоскости. В отличие от свободной конвекции в пористом слое, имеющем изотермальные границы и подогреваемом снизу [9], в рассмотренной модели конвективная устойчивость понижается с увеличением угла наклона. Понижение устойчивости качественно соответствует модели неустойчивости Рэлея–Хадли при уменьшении линейного градиента температуры к верхней поверхности [12]. С увеличением угла наклона меняется и структура конвекции: от многоячеистой, с характерными размерами ячеек по вертикали и горизонтали близкими к единице, переходит к одноячеистой, вытянутой вдоль слоя. Увеличение числа Рэлея–Дарси также способствует реализации одноячеистой структуры, при которой обеспечивается более мощный механизм тепломассопереноса. Таким образом, пространственная ориентация слоя оказывает заметное влияние на устойчивость и развитие конвекции в трещиновато-пористых областях земной коры. Понижение устойчивости с увеличением угла наклона является дополнительным фактором, способствующим развитию и реализации гидротермальной конвекции и проявляющимся в виде аномалий плотности теплового потока на дневной поверхности Земли.

Полученные результаты подтверждают особенности плотности теплового потока над месторождениями нефти и газа, обнаруженные другими авторами [1]. Ориентация слоя и глубина залегания качественно влияет на профили плотности теплового потока. Так, для слоя с небольшим углом наклона при сравнительно небольшой положительной аномалии относительно фона характерна сопоставимая по амплитуде отрицательная аномалия. Такая особенность может свидетельствовать о выделении структурных форм в виде моноклиналей и синклиналей.

Автор благодарит профессора Ю.В. Хачая за внимание к работе и обсуждение результатов.

Работа выполнена при финансовой поддержке Комплексной программы УрО РАН (проект № 15-18-5-32).